Тэк-с. В прошлый раз мы разбирали, что такое нейросети и как они используются. В этой статье увидим, как они обучаются, это удивительный процесс. Что надо знать из прошлой статьи:
- Нейросеть — это просто большая куча формул. Загружаешь в нейросеть данные на входе, она их перемещает внутри себя по формулам и выдаёт результат вычислений.
- Нейросеть не понимает, что она творит. Она просто умножает числа на коэффициенты по формулам. А вот люди уже интерпретируют результаты нейросети так, как им нужно.
- Суть обучения нейросети — задать нужные формулы, чтобы при вводе определённого типа данных мы получали достаточно качественные результаты вычислений.
- Обучение происходит на большом массиве данных: закидываем в нейросеть много задач с одного конца и много правильных ответов к этим задачам с другого конца. С помощью специального математического колдовства нейронка учится выдавать правильные ответы не только на эти задачи, но и на другие похожего вида.
Теперь пошагово, как это происходит.
Возьмём такую ситуацию. У нас есть данные о людях, которые живут в определённом районе: мы знаем их зарплату. Наша задача — предсказать вероятность того, что эти люди закажут такси. У нас есть данные о 10 тысячах человек. И в отдельном файле у нас лежат настоящие вероятности: как эти 10 тысяч человек на самом деле заказывали такси.
Построим самую примитивную нейросеть, которая может существовать (на практике таких нет вообще, но в нашем случае для наглядности можно это изобразить). На входе у нас зарплата. На выходе у нас вероятность того, что человек закажет такси:
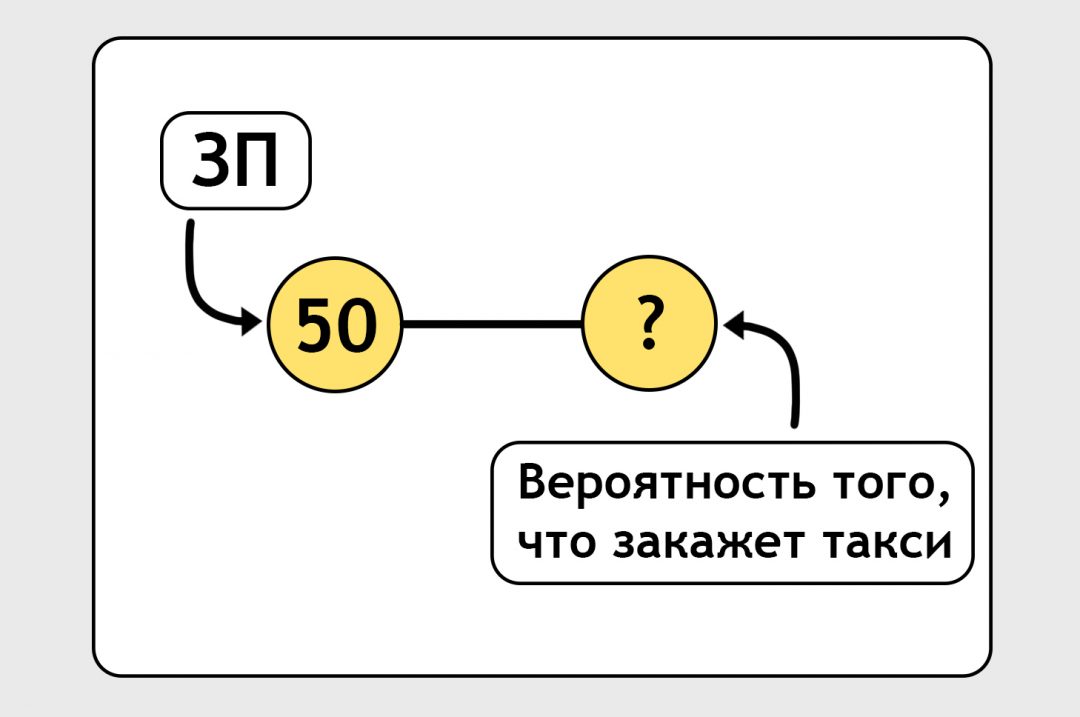
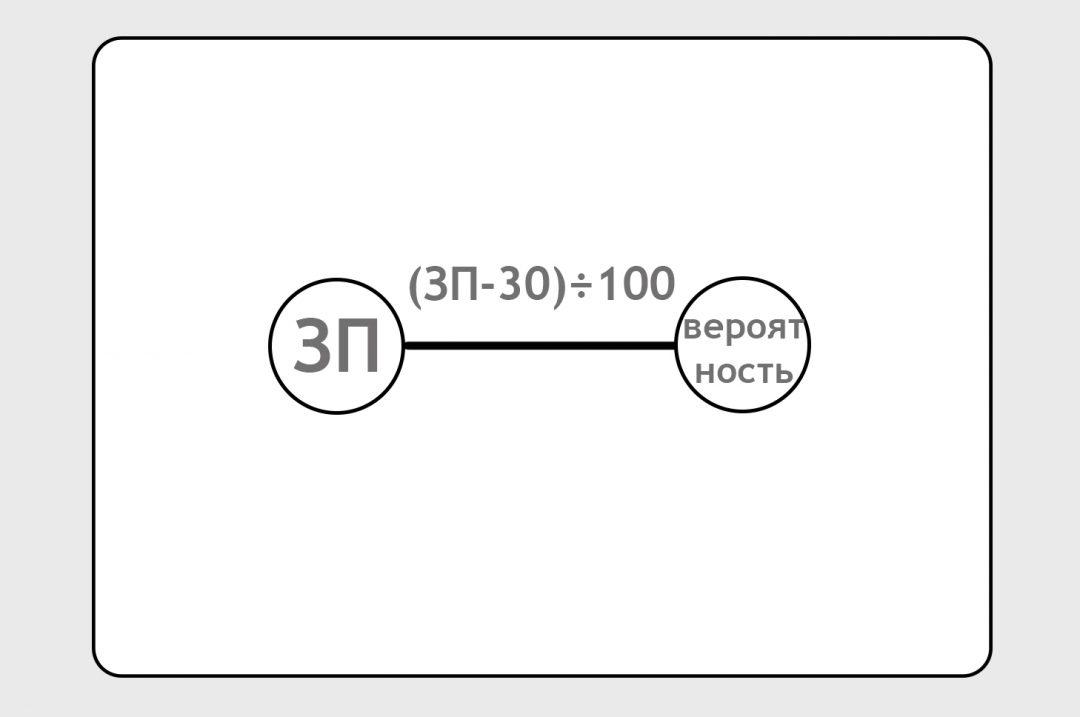
Вход и выход связаны линией. На самом деле это не линия, а формула. По этой формуле нейронка должна обработать входную зарплату и выдать предсказание. Сейчас мы написали формулу от фонаря, просто ткнули пальцем в небо:
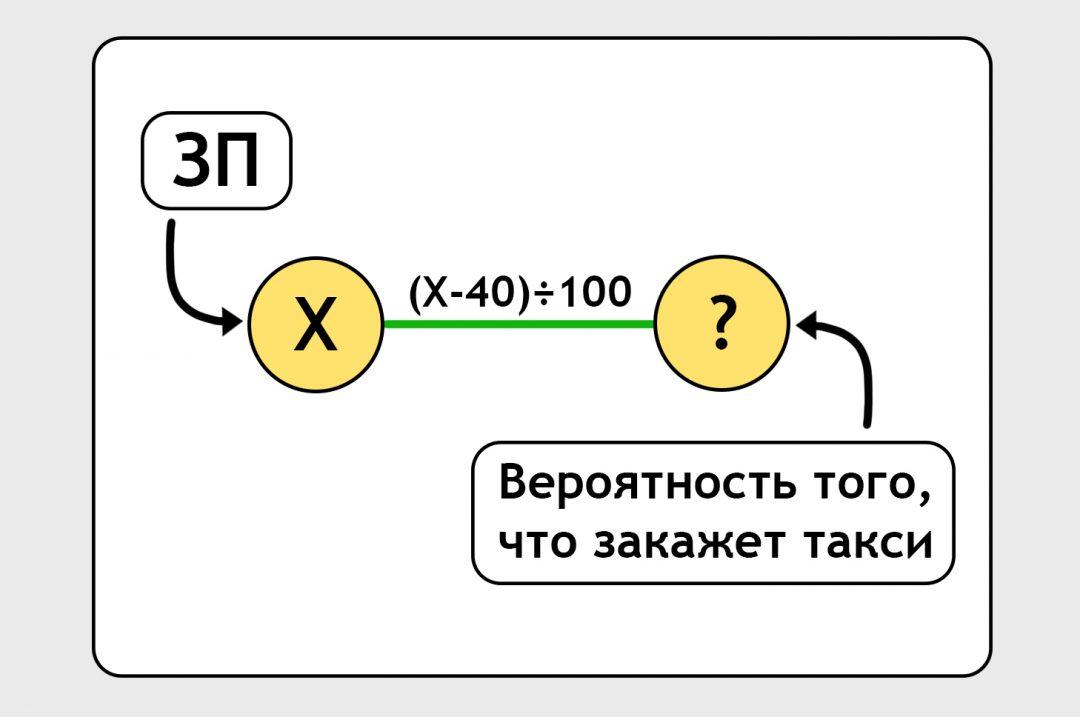
Наша задача — уточнить эту формулу так, чтобы она давала какое-то более-менее правильное предсказание:
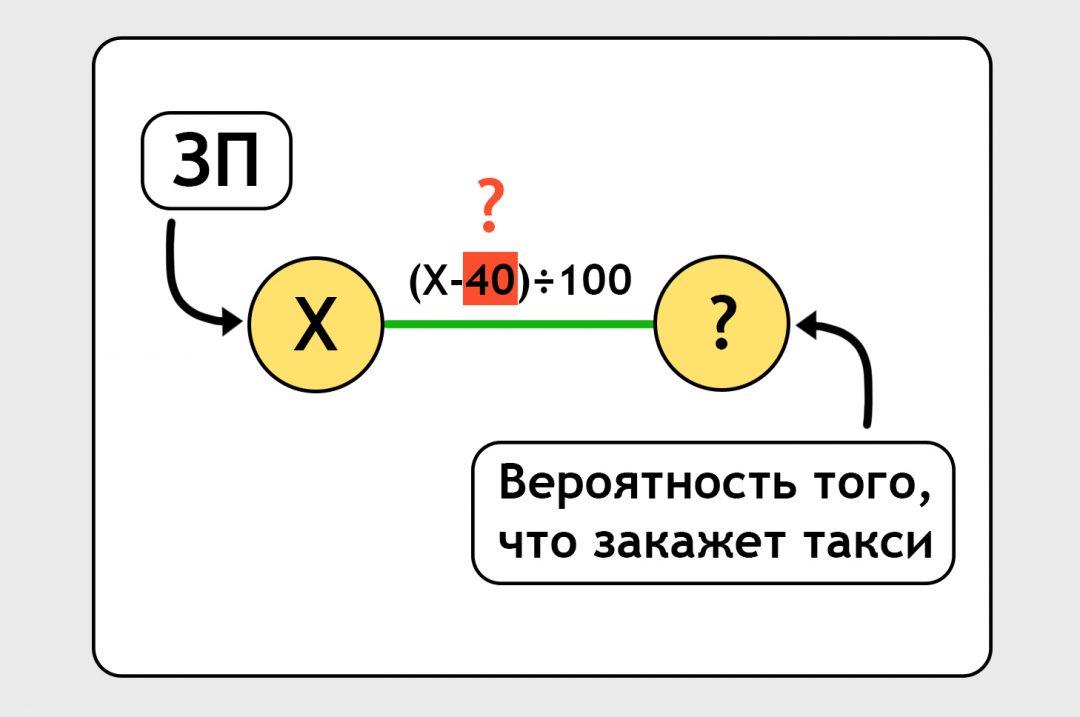
Пока мы не знаем, насколько правильная наша формула. Мы говорим нейросети: «Посчитай хоть что-то», и нейронка считает по той случайной формуле, с которой мы начали. По этой случайной формуле вероятность оказывается 10%:
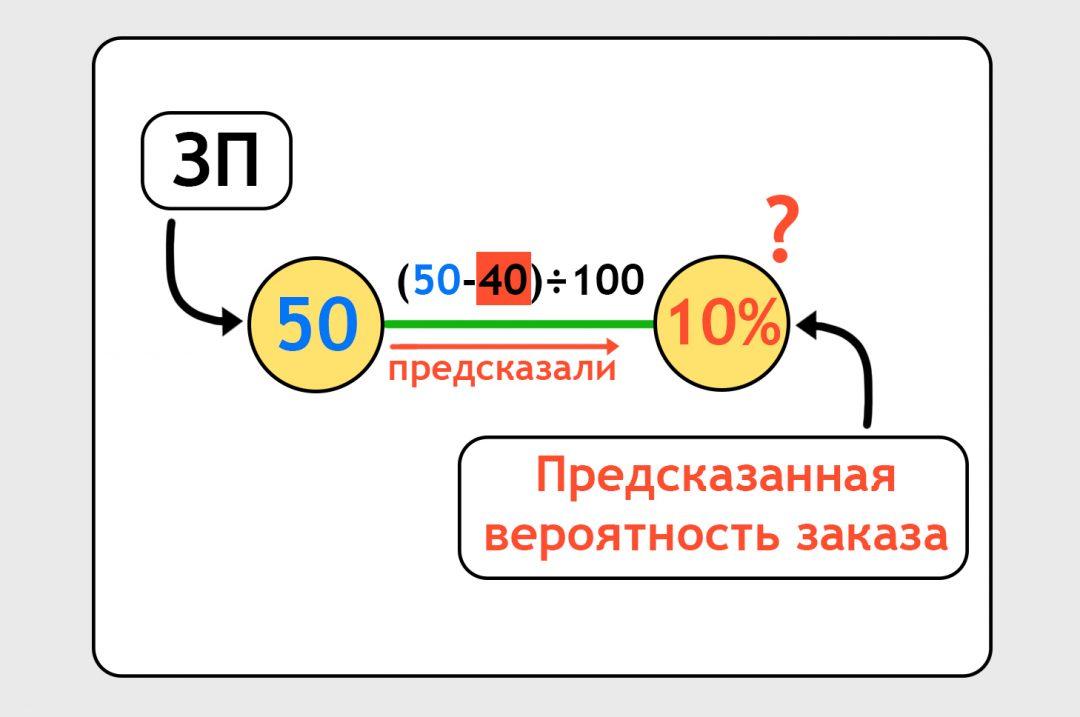
Нейронка предсказала нам, что человек с зарплатой 50 тысяч закажет такси с вероятностью 10%. А мы знаем из другого файлика, что на самом деле он закажет такси с вероятностью 20%:
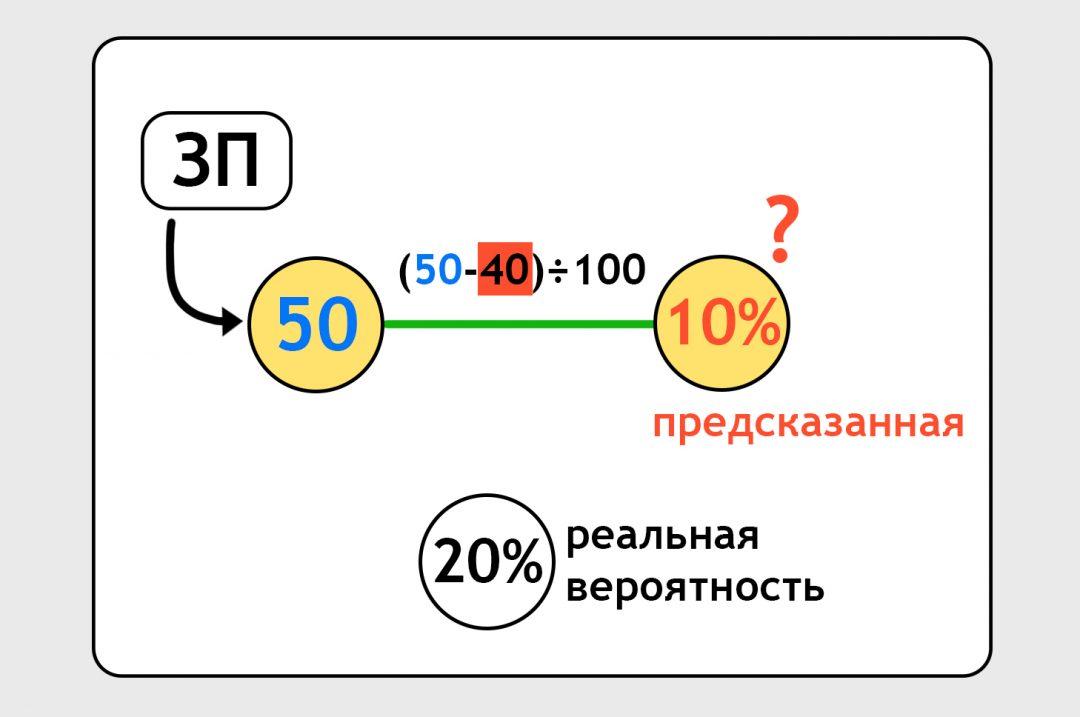
Нам нужно сделать так, чтобы в следующий раз нейронка предсказала более точно. Для этого есть механизм обратного распространения: мы бьём по нейронке палкой и говорим «Исправляйся». Формула корректируется. Это похоже на то, как когда вы решали уравнения на алгебре, заглянули в ответы и увидели, что у вас неправильно. Теперь надо подогнать решение под ответ. Здесь всё то же самое:
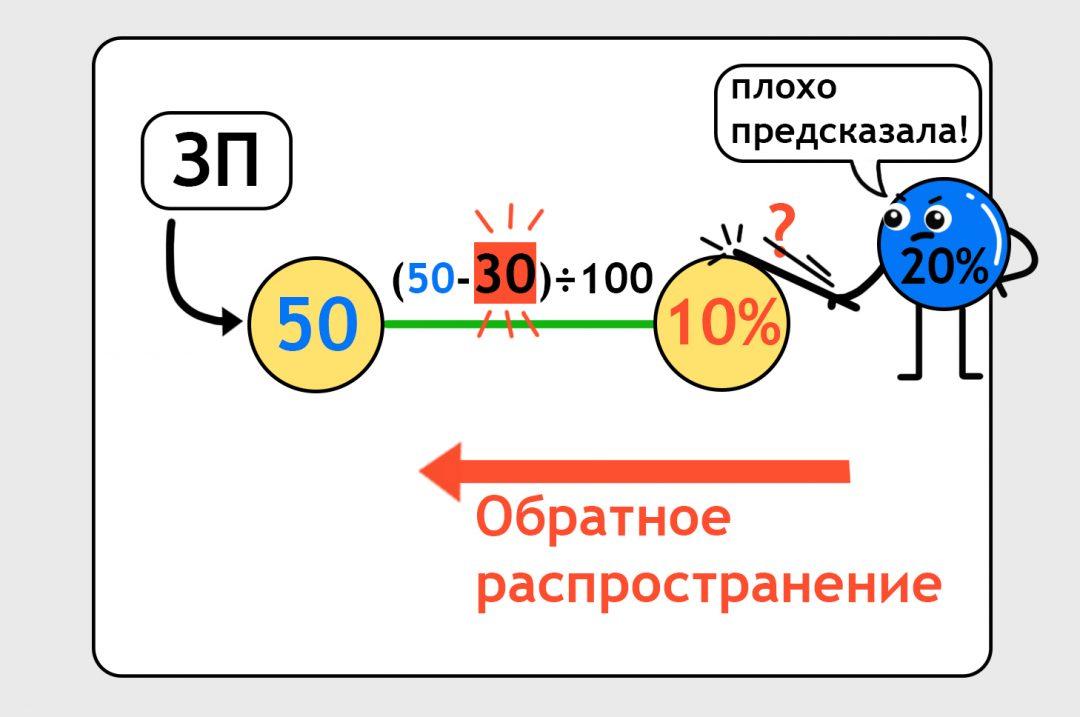
Теперь можно попросить нейронку снова сделать предсказание, уже по скорректированной формуле. Нейронка делает предсказание, оно совпадает с правильными данными, нейронка берёт с полки пирожок:
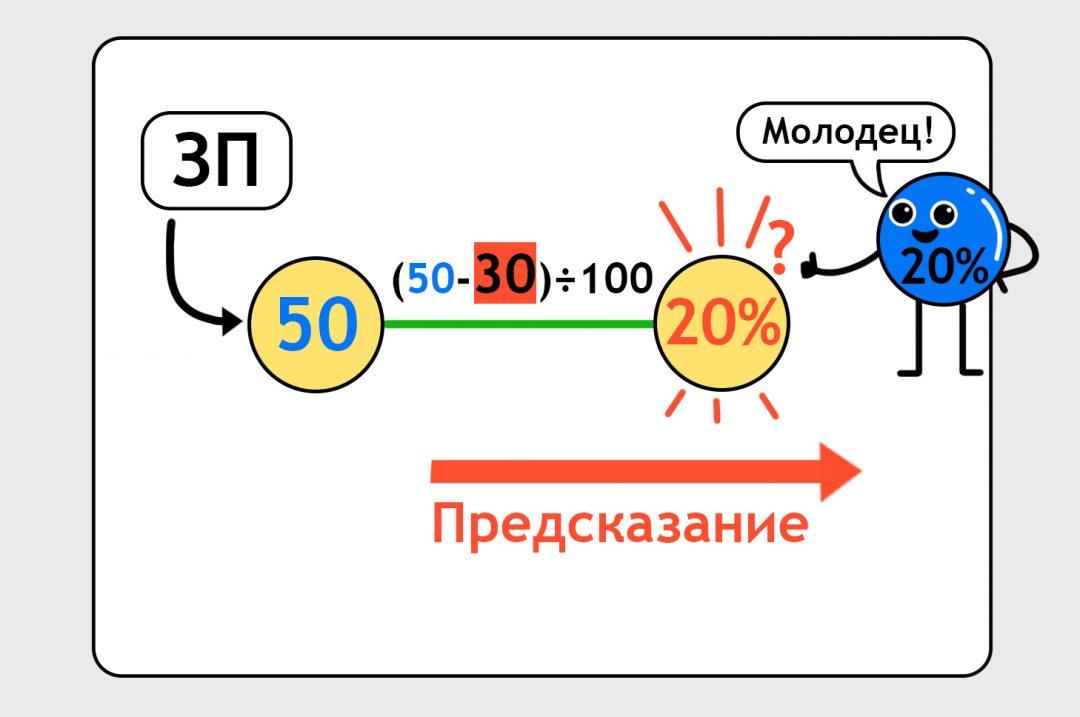
Получается, что мы обучили простейшую нейронку на одной точке данных. У нас одна формула, одна переменная с данными, одна переменная с предсказанием. Это суперпросто, в жизни так просто не бывает. Но пока что можно порадоваться первым шагам:
А что если у нас на входе не одна единица данных, а три? Например, мы знаем о своих пользователях не только зарплату, но и расстояние до ближайшей станции метро и число кошек в доме. Расстояние до метро обозначим как D (например, это будут минуты ходьбы, но с точки зрения нейронки это неважно). Число кошек обозначим как C. Соединим эти данные с предсказанием и вбросим формулы от фонаря. Сделаем предсказание:
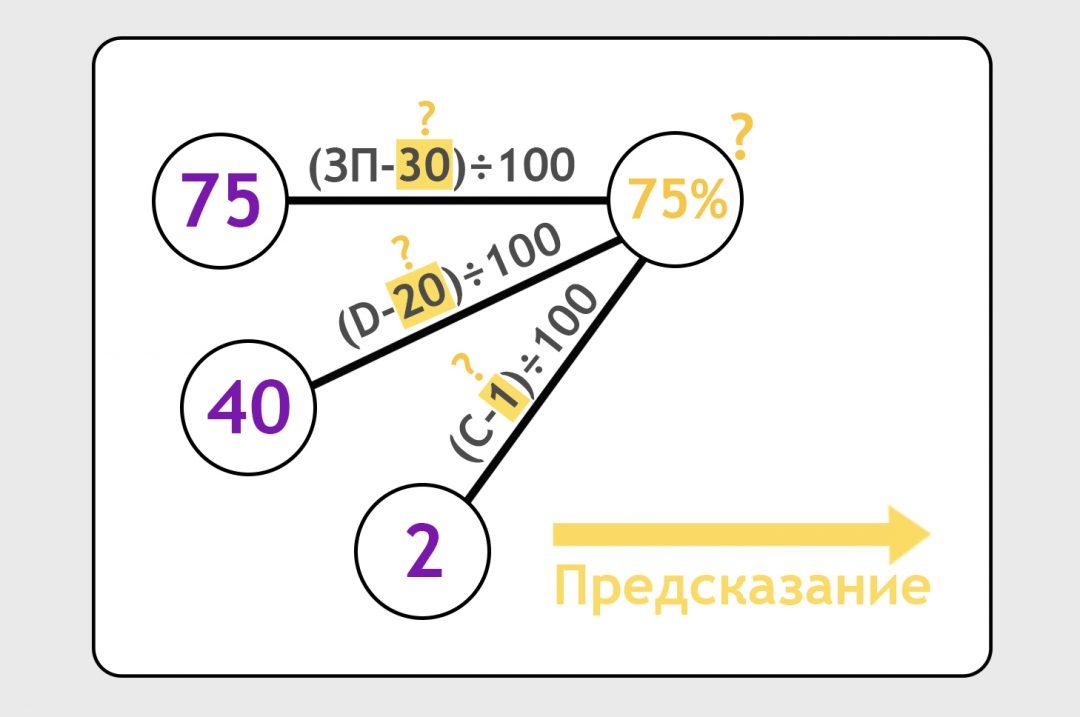
Допустим, для конкретного человека с зарплатой 75 тысяч рублей, который живёт в 40 минутах от метро и у которого есть дома две кошки, вероятность заказать такси — 50%. Наша модель с формулами от фонаря предсказала 75%. Стукнем её палкой, пусть подгонит ответ:
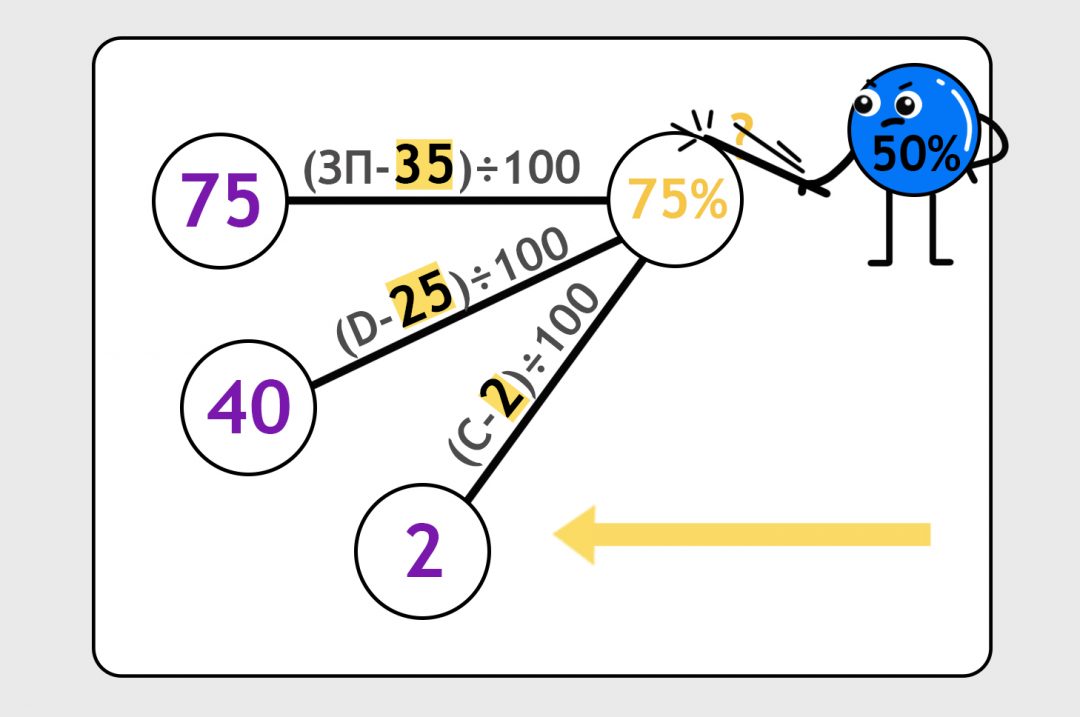
И теперь будем гонять этот процесс туда-сюда на всех наших данных: предсказываем, сверяем с правильным ответом, подгоняем формулы.

После 10 тысяч кругов обучения мы увидим, что нейроночка предсказывает заказы по нашим клиентам с точностью 96%. Мы считаем это достаточно хорошим результатом для этой нейронки. Как она приходит к этому результату и какие ей пришлось делать корректировки в своих формулах, мы не знаем и нам неинтересно. Нам главное, что нейронка предсказывает более-менее точно.
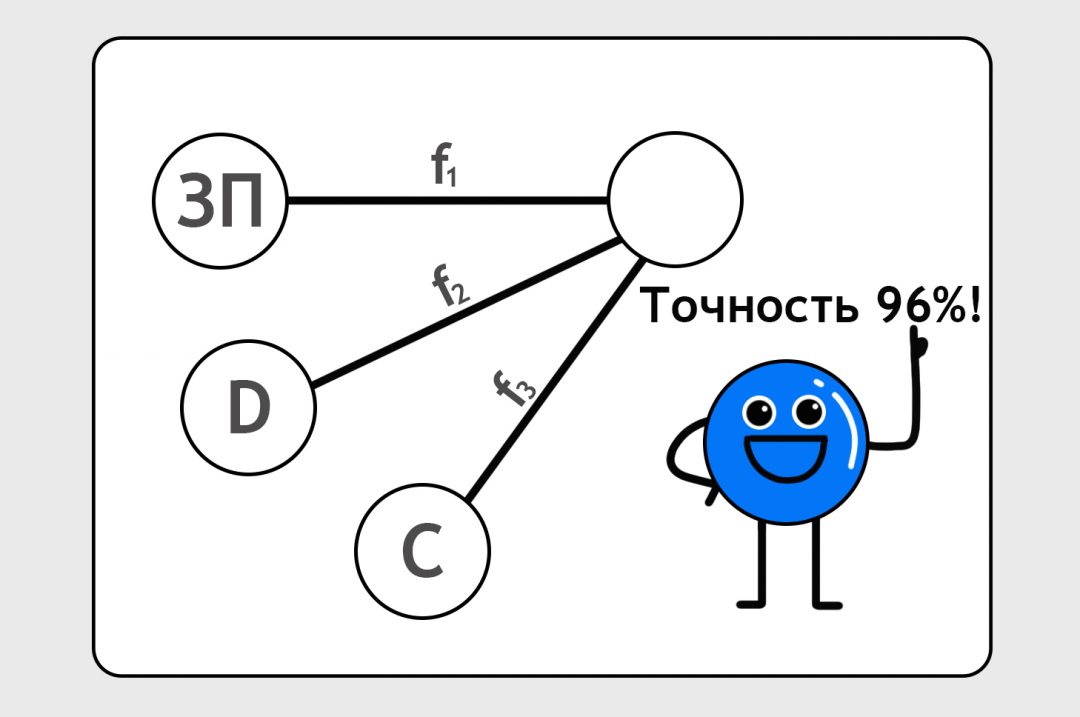
Сейчас наша нейронка слишком простая, в жизни таких простых не бывает, и в реальности она не смогла бы достичь нужной нам степени точности. Выходному узлу тяжело балансировать всё самому, по нему слишком много бьют палкой.
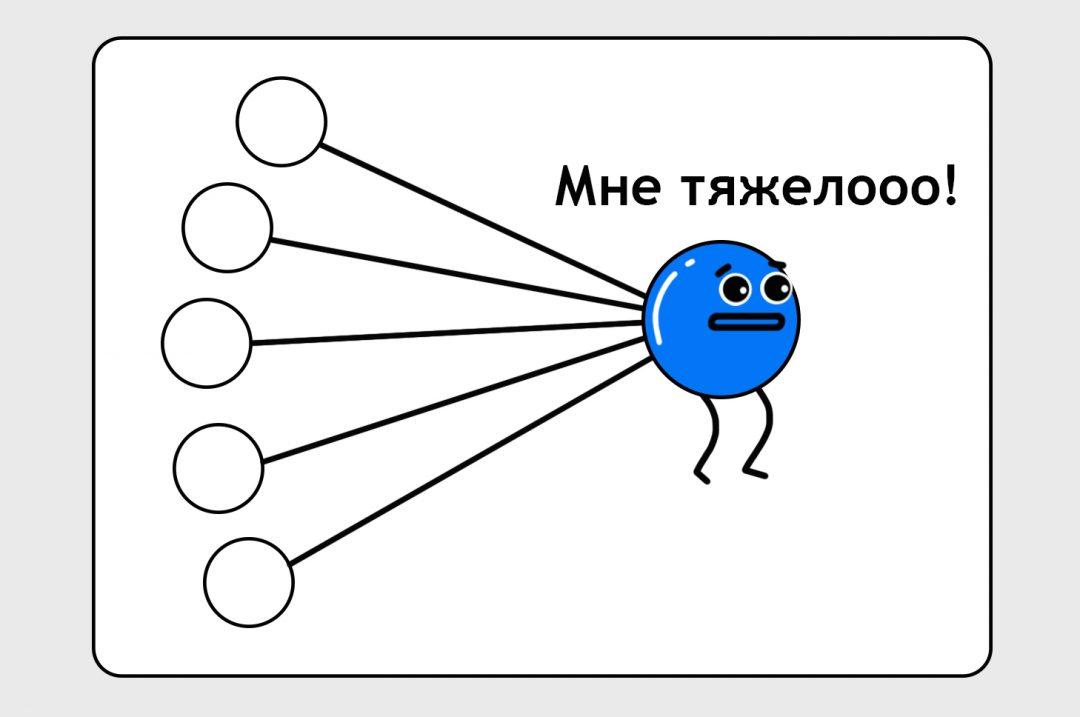
Чтобы нейроночка была точнее, ей добавляют скрытый слой — это как бы промежуточный набор точек для вычисления более сложных штук:
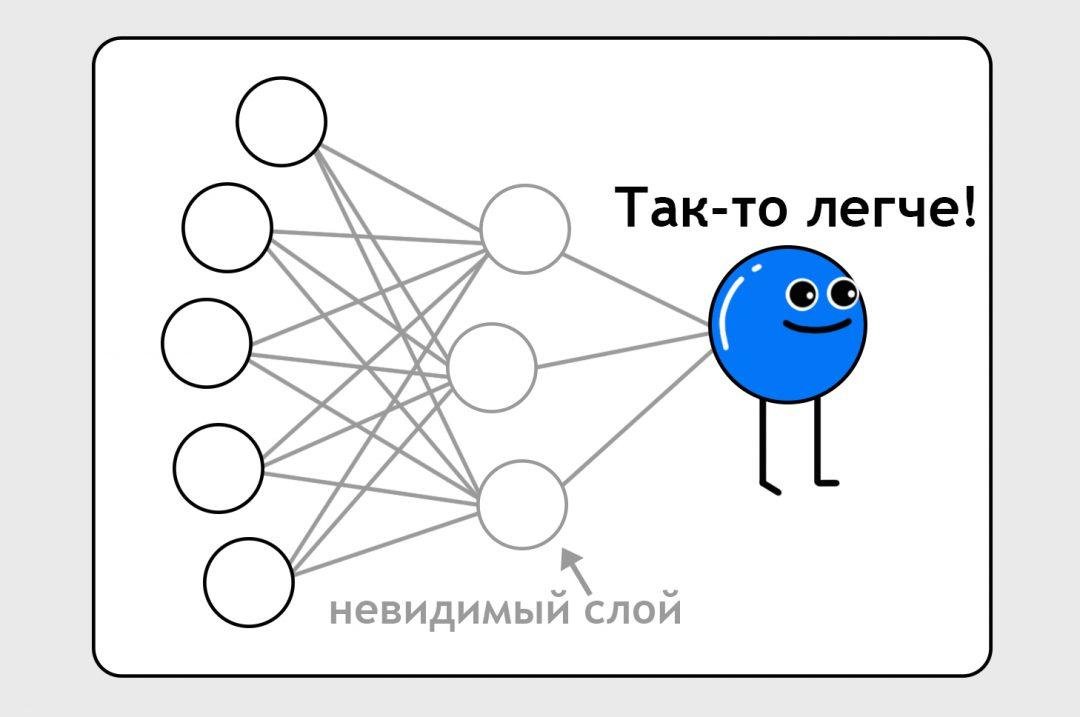
На этом этапе нам уже неважно, что содержится в этом невидимом слое и в связях между этими нейронами. Мы знаем, что если у нас есть 10 тысяч точек данных и достаточно нейронных связей, мы можем обучить нейронку чему угодно.
Поэтому мы вбрасываем на нейронные связи какие-то случайные формулы (это называется инициализацией), заставляем нейронку делать предсказания и бьём по ней палкой, когда предсказания неверны:
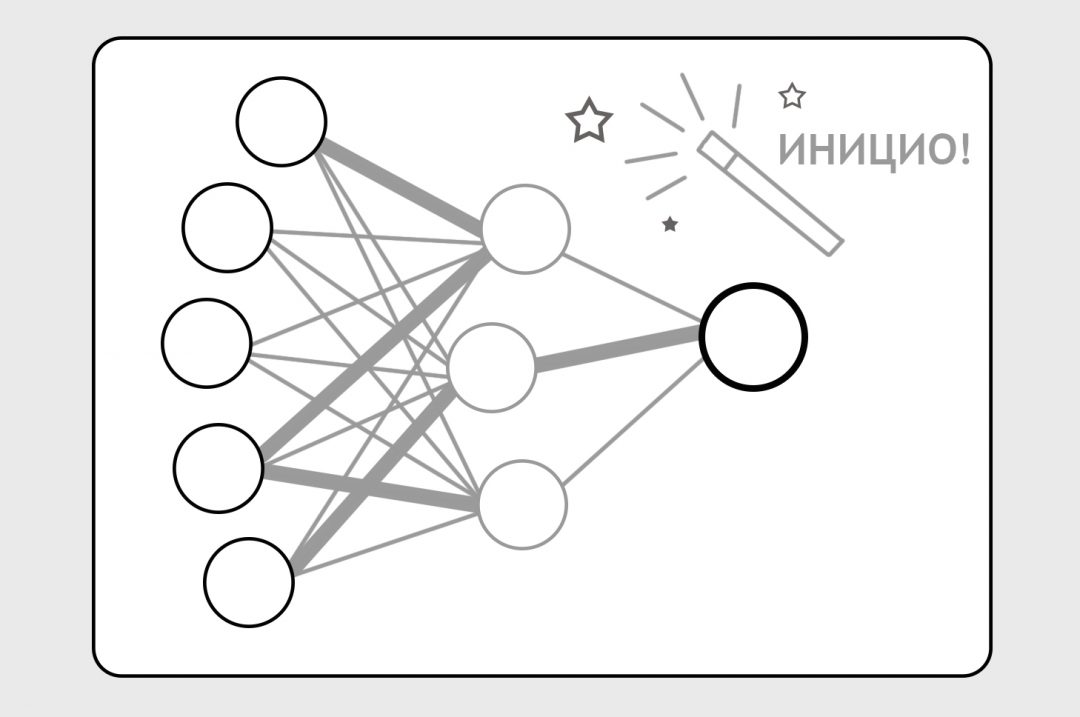
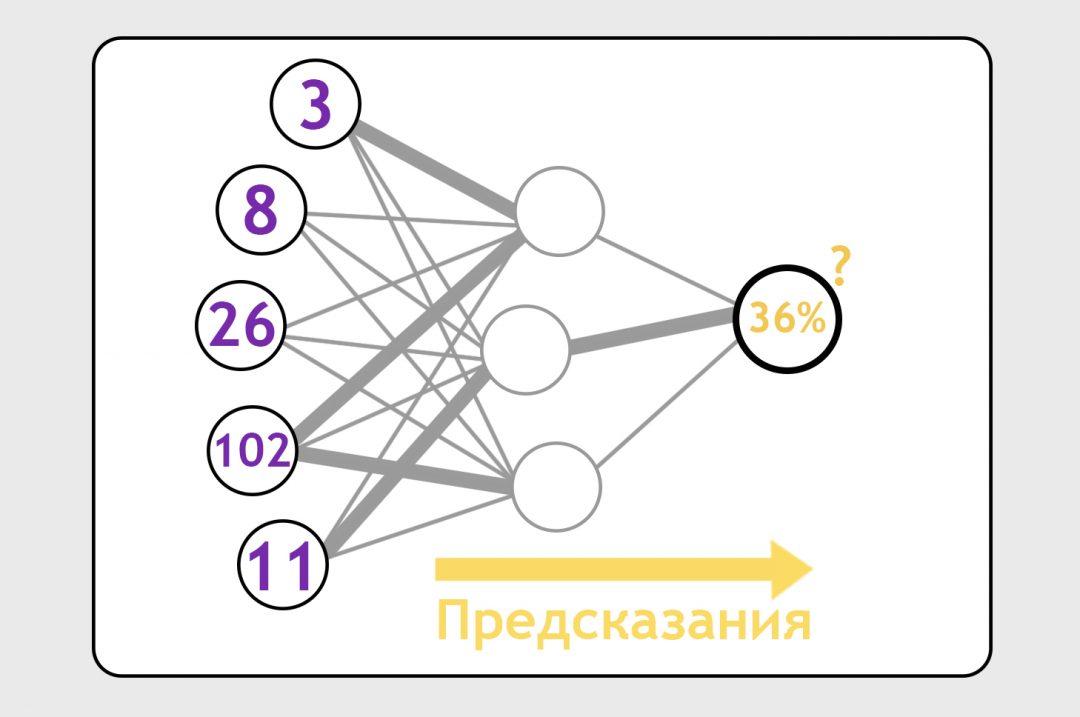
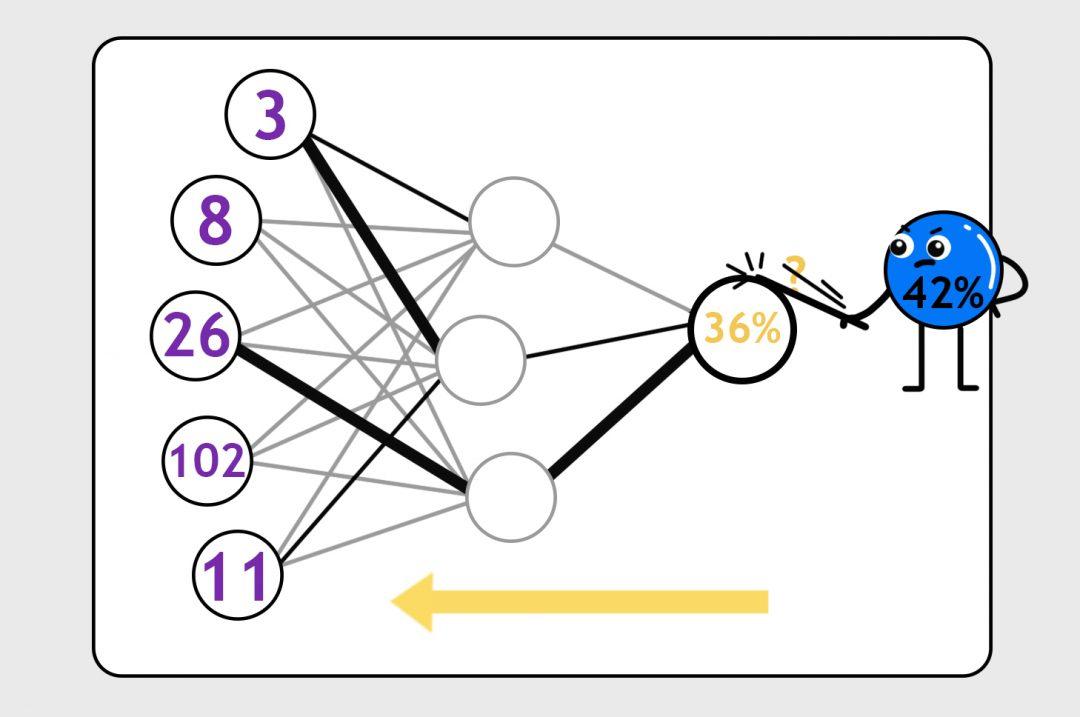
С каждым прогоном какие-то нейронные связи становятся сильнее, другие — слабее, формулы с каждым прогоном становятся всё точнее. В итоге нейронка учится делать предсказания с нужной нам степенью точности.
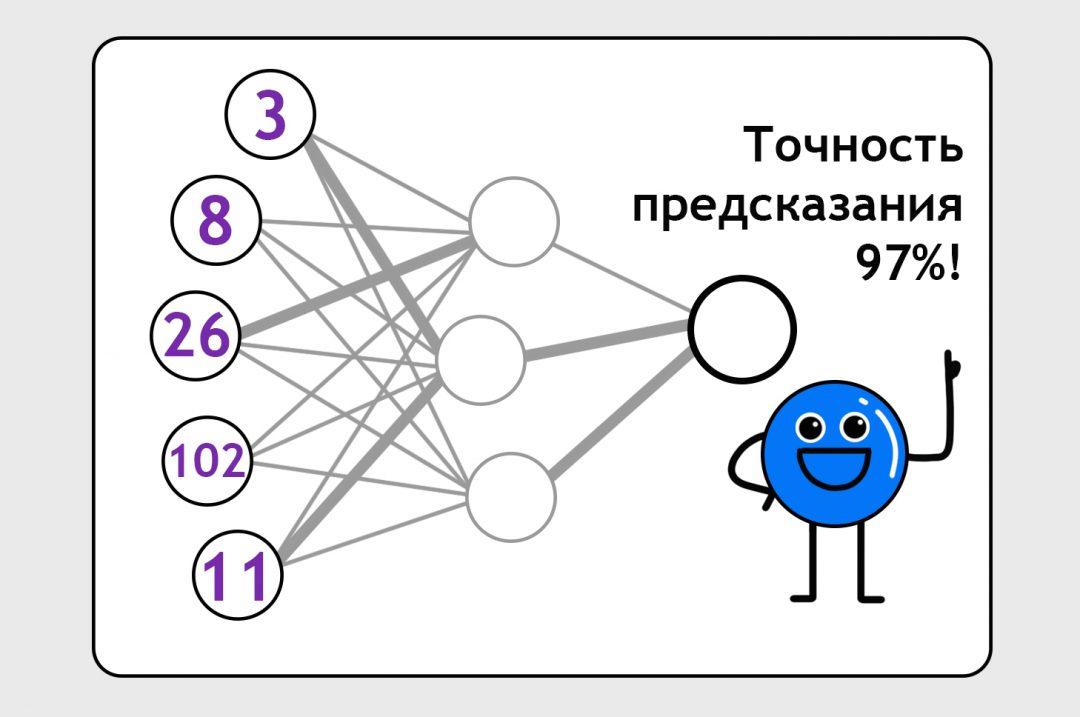
Вот и всё. Нейросети — это тупой перебор, подгон решения под ответ и жёсткая дисциплина.