Продолжаем рассказывать о разных видах алгоритмов сортировок. Мы уже разобрали самую простую пузырьковую сортировку и теперь улучшаем её — пишем сортировку расчёской.
Коротко про пузырьковую сортировку
Самый простой способ сортировки, который работает по такому принципу: берутся два элемента, сравниваются между собой и сразу меняются местами, если второй больше первого. Называется так потому, что это похоже на пузырьки воздуха в воде, которые всплывают наверх.
Если представить числа в виде столбиков, в зависимости от их размера, то пузырьковая сортировка будет выглядеть так:
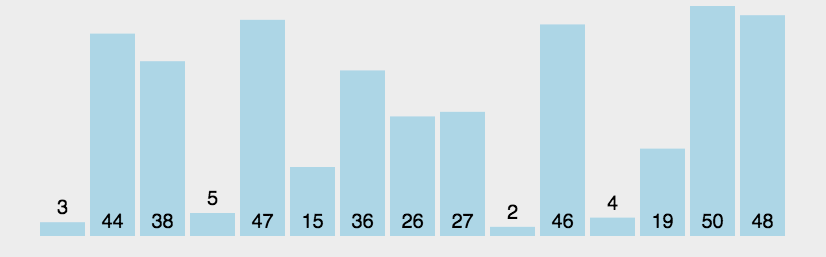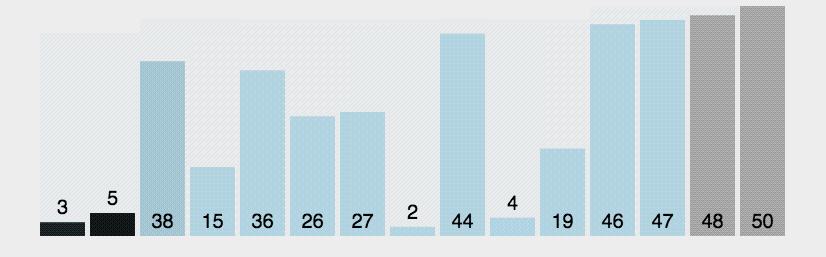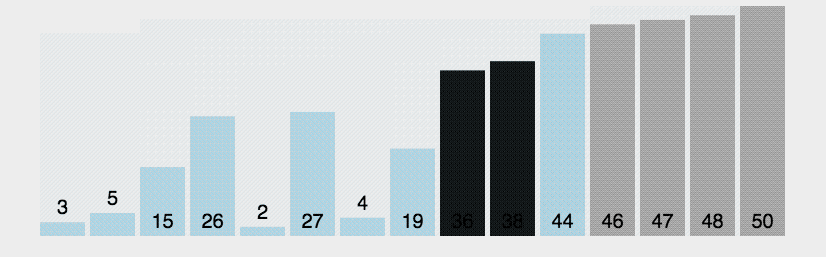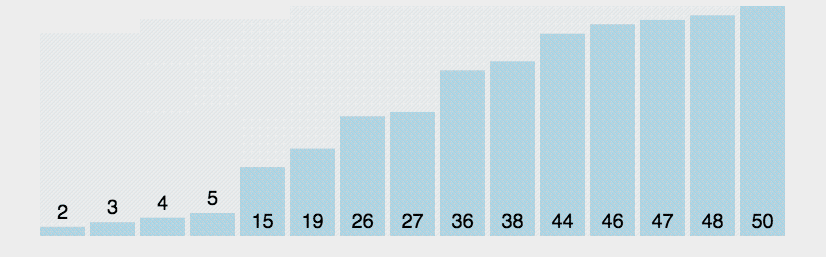
Чем плоха пузырьковая сортировка
Главный недостаток пузырьковой сортировки — её скорость и полный перебор всех элементов массива. Скорость работы алгоритма зависит не от количества сравнений (они выполняются быстро), а от количества перестановок (на них как раз и тратится много процессорного времени).
Получается, что если у нас в массиве в начале будет много больших элементов, которые нужно отправить в конец массива, то каждый раз нам придётся менять их местами с соседями, по одной перестановке за раз. Можно представить, что мы несем куда-то не слишком тяжёлый ящик, но после каждого шага ставим этот ящик на пол, потом поднимаем, делаем шаг, снова ставим, снова поднимаем. Процедуры простые, но из-за устройства алгоритма мы делаем эти процедуры слишком много раз.
В чём хитрость сортировки расчёской
Раз у нас большие элементы могут тормозить весь процесс, то можно их перекидывать не на соседнее место, а подальше. Так мы уменьшим количество перестановок, а с ними сэкономим и процессорное время, нужное на их обработку.
Но отправлять каждый большой элемент сразу в конец массива будет недальновидно — мы же не знаем, насколько этот элемент большой по сравнению с остальными элементами. Поэтому в сортировке расчёской сравниваются элементы, которые отстоят друг от друга на каком-то расстоянии. Оно не слишком большое, чтобы сильно не откидывать элементы и возвращать потом большинство назад, но и не слишком маленькое, чтобы можно было отправлять не на соседнее место, а чуть дальше.
👉 Опытным путём программисты установили оптимальное расстояние между элементами — это длина массива, поделённая на 1,247 (понятное дело, расстояние нужно округлить до целого числа). С этим числом алгоритм работает быстрее всего.
Как работает алгоритм сортировки расчёской
На первом шаге мы находим длину массива (например, 10 элементов) и делим её на 1,247. Допустим, после округления у нас получилось число 8. Теперь мы проходим первый цикл пузырьковой сортировки, только сравнивая не 1 и 2, 2 и 3, а сразу 1 и 8, 2 и 9, 3 и 10. Это отправит самые большие числа, если они есть в начале, в самый конец. Всего на первом шаге будет три сравнения.
На втором шаге мы берём число 8 из предыдущего этапа и снова делим его на 1,247, получая число 6. Теперь мы снова проходим весь массив и сравниваем так:
1 и 6
2 и 7
3 и 8
4 и 9
5 и 10
Уже получилось 5 перестановок и снова крупные числа улетели поближе к концу массива.
Так мы уменьшаем размер шага до тех пор, пока он не станет меньше единицы — к этому моменту массив будет полностью отсортирован.
🤔 Сортировка расчёской называется так из-за того, что мы как бы расчёсываем массив сначала широким гребнем (большой шаг), потом гребнем поменьше (шаг поменьше). В конце шаг равен единице, как в пузырьковой сортировке.
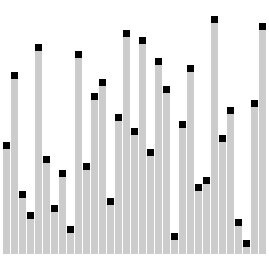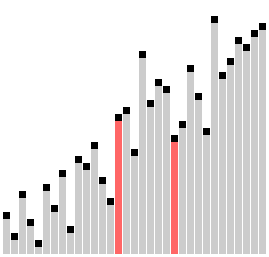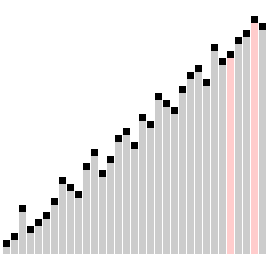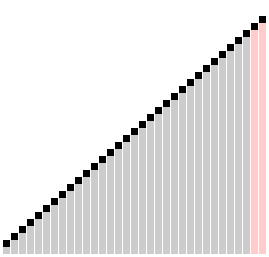
Сортировка расчёской на JavaScript
Запустите этот код в консоли браузера, чтобы посмотреть, как алгоритм шаг за шагом приводит массив в нормальный вид:
// исходный массив
var arr = [3,14,1,7,9,8,11,6,4,2]
// получаем длину массива
const l = arr.length;
// оптимальное число для вычисления шага сравнения
const factor = 1.247;
// получаем точный шаг сравнения
let gapFactor = l / factor;
// пока шаг больше единицы
while (gapFactor > 1) {
// округляем шаг до целого
const gap = Math.round(gapFactor);
// и организуем цикл как в пузырьковой сортировке
for (let i = 0, j = gap; j < l; i++, j++) {
// если сначала идёт большое число
if (arr[i] > arr[j]) {
// меняем их местами
[arr[i], arr[j]] = [arr[j], arr[i]];
}
// выводим текущее состояние массива в консоль
// это необязательный шаг, он здесь для наглядности
console.log(arr);
}
// в конце цикла рассчитываем новый шаг
gapFactor = gapFactor / factor;
}Почему это лучше пузырьковой сортировки, ведь алгоритм выглядит сложнее и в конце мы всё равно сравниваем соседние элементы?
То, что код выглядит сложнее, ничего не значит: нам нужна не оценка сложности кода, а скорость и эффективность работы.
Расчёска лучше пузырьковой сортировки, потому что в ней намного меньше операций перестановки. Именно перестановка занимает основное время процессора. В самом худшем случае алгоритм сортировки расчёской будет работать так же, как и пузырьковая, а в среднем — алгоритм работает быстрее пузырьковой.