У многих современных мессенджеров есть шифрование в режиме end-to-end. Это значит, что сообщения шифруются на одном устройстве и через сервер отправляются другому человеку, который может их расшифровать. Кроме отправителя и получателя прочитать такое сообщение никто не может, потому что они используют стойкое симметричное шифрование. Проще говоря, сообщение шифруется неким ключом и расшифровывается таким же ключом.
У этого способа есть один минус — нужно как-то заранее обменяться общим ключом. Для решения этой проблемы используют асимметричное шифрование. Оно позволяет выработать общий ключ и передать его в зашифрованном виде каждой стороне даже в условиях прослушивания канала передачи.
Вот это и разберём.
👉 Слегка упрощённо. В статье мы опустили протоколы аутентификации и проверки подписей и отпечатков открытых ключей. Ещё здесь нет постоянной смены общего ключа и его генерации по запросу. Если вы занимаетесь криптографией, можете не читать — ничего нового вы для себя не узнаете.
Протокол Диффи-Хеллмана (математика)
Главная задача мессенджера при первом обращении — получить общий секретный ключ. Это можно сделать с помощью протокола Диффи — Хеллмана.
Принцип работы этого протокола Уитфилд Диффи и Мартин Хеллман опубликовали в 1976 году, и с тех пор он лежит в основе всех подобных алгоритмов получения общего секретного ключа.
Сейчас покажем этот алгоритм с помощью математики, а потом приведём аналогию с цветом.
Допустим, Алла хочет тайно переписываться с Борисом, но они могут пользоваться только незащищённым каналом связи. Это значит, что всё, что они отправляют, может перехватить злоумышленник и попытаться расшифровать. В таких условиях они не могут просто послать друг другу секретный ключ, потому что его сразу узнает тот, кто за ними следит.
В этом случае Алла говорит Борису: придумай себе большое простое число и никому его не говори, а я придумаю пока своё. Какие числа выберут Алла и Борис — никто не знает, потому что они их не пересылают друг другу, а просто договариваются о выборе. Это будет для каждого свой секретный ключ, который они используют для асимметричного шифрования, a — для Аллы и b — для Бориса.
Когда оба выбрали себе по ключу, Алла говорит: Борис, вот два простых числа, P и G, работать будем с ними. В этот момент тот, кто прослушивает канал, может получить себе эти числа, но это ему ничего не даст. Почему не даст — увидите дальше.
Когда Борис получил эти числа, Алла говорит Борису:
- Возведи G в степень своего секретного числа b
- Найди остаток от деления этого результата по модулю P
- То, что получилось, пересылай мне.
Если записать это языком математики, то у Бориса получается такое:
Gb mod P = B ← вот это число B Борис и отправляет Алле.
Алла одновременно с Борисом делает то же самое со своим секретным числом и отправляет результат Борису:
Ga mod P = A ← вот это число A Алла отправляет Борису.
Деление по модулю
Остаток от деления по модулю означает следующее: мы делим одно число на другое с остатком. Целую часть выкидываем, а остаток — это то, что нам нужно. Обозначается такое деление словом mod.
Например, 12 mod 5 = 2, потому что 12 = 2×5 + 2
13 mod 4 = 1, потому что 13 = 4×3 + 1
10 mod 2 = 0, потому что 10 = 2×5 + 0
В криптографии деление по модулю применяется часто, потому что зная два исходных числа найти остаток очень легко, а вычислить первое число, зная второе и остаток — невозможно.
Если X mod 5 = 1, то X может быть равен 6, 11, 16, 21 и так далее — остаток от деления каждого из этих чисел по модулю 5 равен одному. Поэтому пересылать остаток от деления по модулю можно, а первое число — нет.
Когда Алла и Борис получили друг от друга их остатки от деления по модулю, они применяют ту же самую операцию к этому остатку. Даже если кто-то перехватит эти остатки от деления, он не восстановит по ним секретные ключи Аллы и Бориса.
В итоге оба собеседника получают одно общее число, которое можно использовать как общий ключ для симметричного шифрования. Как у них получается одинаковое число — следите за математической магией:
- Алла берёт результат Бориса B и делает так: Ba mod P = K.
- Но Ba mod P = Gba mod P → запомним это.
- Борис берёт результат Аллы А и делает так: Ab mod P = K.
- Но Ab mod P = Gab mod P → запомним и это.
- От перестановки множителей результат не меняется, а в обоих случаях мы возводим G в степень ab, поэтому у Аллы и Бориса получается в итоге одно и то же число. Это и есть их общий ключ для симметричного шифрования, которым они теперь могут пользоваться.
Штука в том, что без секретных ключей Аллы и Бориса кто-то другой не сможет вычислить этот ключ, даже если перехватит все сообщения с промежуточными результатами. А всё потому, что никто из них свои секретные ключи никуда не передавал.
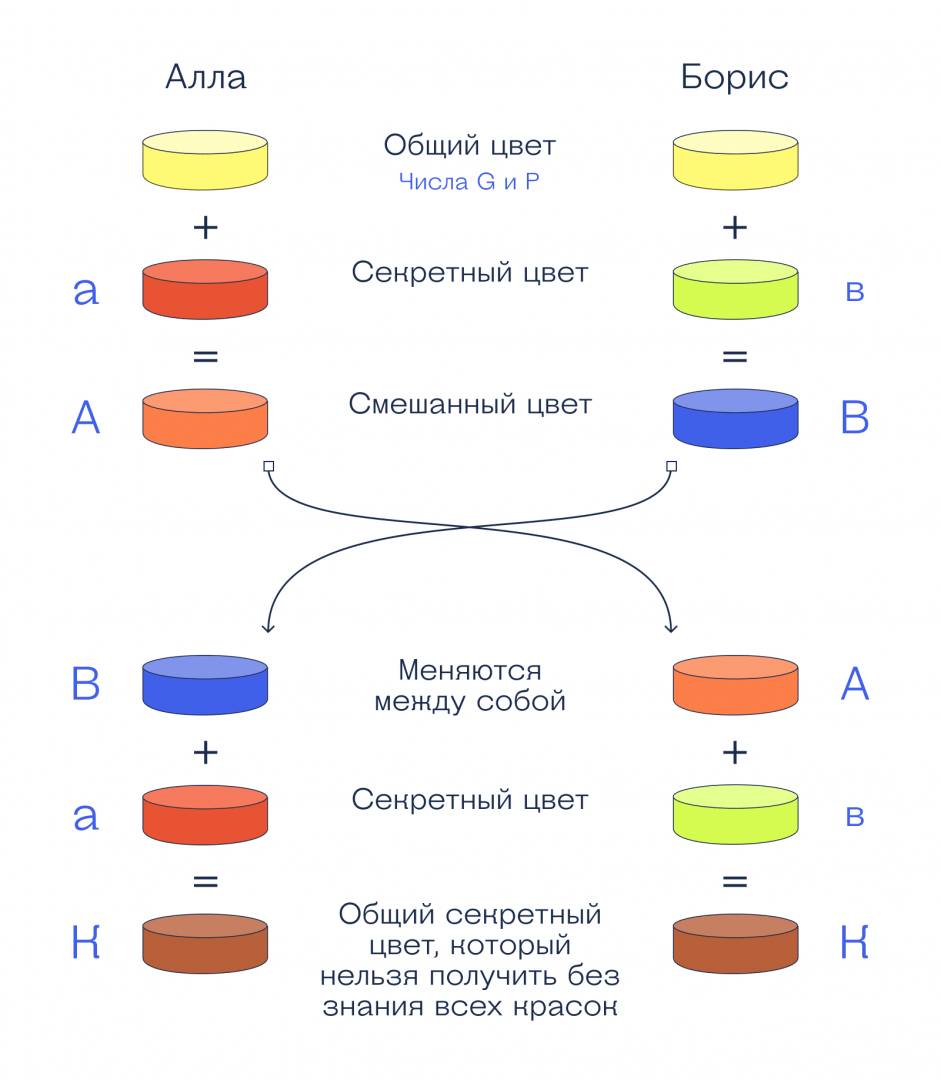
Пример с цветами
Если математика показалась слишком сложной, вот пример с красками. Предположим, что мы можем легко перемешивать краски между собой, но при этом по готовой краске нельзя точно определить, какие именно оттенки использовались при смешивании. Тогда вся схема шифрования будет выглядеть так:
Этот алгоритм гарантирует защиту от взлома и тайну переписки?
Нет, сам алгоритм нужен только для создания пары ключей. Если кто-то посередине будет всё подслушивать, он может перехватить все промежуточные результаты и подменить их своими. В итоге Алла и Борис установят промежуточную секретную связь через злоумышленника, который будет читать всю их переписку, а Алла и Борис ничего не заметят.
И что делают, чтобы такого не было?
Используют алгоритмы аутентификации и проверки цифровой подписи. Как это работает — отдельная сложная история. Если коротко: есть специальные алгоритмы, которые позволяют проверить, действительно ли этот ключ отправила Алла, а не кто-то другой вместо неё.
Так переписка в мессенджерах безопасна или нет?
Зависит от настроек сервера. Если сервер действует честно и просто переправляет сообщения, то, скорее всего, да. Если же сервер вклинивается и становится промежуточным звеном, как в примере выше, то кто угодно на сервере может читать вашу переписку.
Проще относиться к любой переписке как к публичной, а не полагаться на алгоритмы. Хотите что-то держать в секрете — говорите это лично или не говорите совсем.
А как же Телеграм?
В Телеграме полное end-to-end-шифрование реализовано только в секретных чатах и при звонках. Вся остальная переписка тоже защищена, но не настолько сильно. Но всегда есть вероятность, что даже серверы Телеграма тайно вклиниваются в переписку и читают сообщения. Хотите полной приватности — стройте хижину в тайге.
