Динамическое программирование не всегда означает создание компьютерных программ. На самом деле это метод решения задач и одна из фундаментальных парадигм в теории алгоритмов.
Рассказываем подробно и просто, в чём суть, почему это работает и когда он вам не поможет и лучше использовать другой метод.
Что такое динамическое программирование
Динамическое программирование — это метод решения сложной задачи через её декомпозицию. Большой объём работы делится на составляющие, потому что хорошее решение для них найти проще. Результат каждого решения сохраняется и складывается в одно наилучшее.
Динамический подход в алгоритмах можно применять не только в программировании — его используют в экономике, логистике, математике.
В биологии, например, динамическое программирование используют для исследования ДНК. Это последовательности, которые показывают родственные связи, мутации и наследственные заболевания. Кроме ДНК, такие последовательности есть у человеческих белков, с которыми взаимодействуют вирусы, например COVID-19:

Для таких исследований нужно быстро сравнивать огромные генетические последовательности. Решение путём простого перебора тут не подходит, а вот динамическое программирование как раз сильно ускоряет всю работу.
Про работу с такими последовательностями мы ещё расскажем подробнее, а пока разберём основные принципы, почему всё это работает и как именно.
Метод динамического программирования
Почему метод динамического программирования вообще работает? Оно позволяет получить наилучшее решение, которое складывается из маленьких фрагментов.
Принцип оптимальности Беллмана — краеугольный камень ДП
По-научному весь смысл ДП называется «Принцип оптимальности Беллмана» и на сложном языке выглядит длинно и звучит непонятно:
Если управление оптимально, то, каковы бы ни были первоначальное состояние системы и управление системой в начальный момент времени, последующее управление оптимально относительно состояния, которое система примет в результате начального управления.
На деле это значит, что если для большой задачи есть лучшее решение, то все фрагменты этого решения тоже будут лучшими. А из этого следует, что большую задачу сначала можно разбить на части и найти лучшее решение для каждой из них. Если эти части потом сложить, получится одно целое оптимальное решение.
Плюс в том, что много простых ответов искать всё равно намного легче, чем один большой со многими вариациями.
Да, возможно, это всё ещё не совсем понятно, разбираем дальше.
Полезный блок со скидкой
Если вам интересно разбираться со смартфонами, компьютерами и прочими гаджетами и вы хотите научиться создавать софт под них с нуля или тестировать то, что сделали другие, — держите промокод Практикума на любой платный курс: KOD (можно просто на него нажать). Он даст скидку при покупке и позволит сэкономить на обучении.
Бесплатные курсы в Практикуме тоже есть — по всем специальностям и направлениям, начать можно в любой момент, карту привязывать не нужно, если что.
Разбиение на подзадачи и запоминание результатов
Главный фокус в том, что маленькие задачи можно решить быстро и записать результат решения. Нам не нужно запоминать всё решение и то, как мы к нему пришли. Только результат. Из этих ответов мы потом сложим одно целое решение большой задачи.
Простой пример — игра в монеты. На столе лежит случайное количество монет, и два игрока могут забирать по 1 или 2 монеты. Выигрывает тот, кто ходит последним и забирает оставшуюся монету (или две).
У этой игры есть выигрышная стратегия, которую можно найти через динамическое программирование. Для нахождения этой стратегии нужно начать с малого: попробовать найти правильные действия для победы при небольшом количестве монет.
Попробуем:
- При 1 монете мы берём 1 монету и выигрываем.
- При 2 монетах забираем две и выигрываем.
- При 3 монетах так не получится. Мы можем взять только 1 или 2 монеты, а это значит, что нельзя помешать сопернику выиграть: ему всегда остаются 1 или 2 монеты, которые можно забрать за раз.
Эту часть можно и нужно запомнить: при 1 и 2 монетах выигрываем, при 3 — проигрываем.
Продолжая анализ, можно просчитать, что выиграть можно, только если во время нашего хода количество монет на столе не кратно 3. При таком раскладе всё, что нужно, — брать столько монет, чтобы их количество было кратным 3 именно после.
Например:
- На столе 11 монет — берём 2, оставляем противнику 9.
- На столе 7 монет — берём 1, оставляем 6.
- На столе 5 монет — берём 2, оставляем 3.
А при 3 монетах противник уже не может сделать ничего, чтобы могло помешать нам следующим ходом забрать все монеты.
Это и есть метод динамического программирования — мы разбили объёмную задачу на составляющие, запомнили результаты и сразу используем их. Даже при тысячах и миллионах монет нам не нужно перебирать огромное количество вариантов развития игры — нужно только помнить, что после нашего хода на столе должно оставаться количество монет, которое делится без остатка на 3.
Для чего используется динамическое программирование
Динамическое программирование используется во многих сферах. Для наглядности мы разберём несколько примеров, чтобы было видно пользу и принципы работы.
Оптимизационные — разбираем задачу рюкзака
Это задачи, где нужно найти оптимальную комбинацию. Например, подобрать лучший набор вещей для рюкзака в путешествие, когда вместимость ограничена, а каждая вещь имеет разную ценность.
Если бы мы решали эту задачу способом динамического программирования, это бы выглядело так.
У предметов уже есть понятная ценность и занимаемый объём или вес, например:
- Палатка — 6 килограмм, ценность 8.
- Еда — 5 килограмм, ценность 7.
- Спальник — 4 килограмма, ценность 5.
- Вода — 3 килограмма, ценность 4.
- Фонарь — 2 килограмма, ценность 3.
Наша цель — набрать предметы так, чтобы не превысить 10 килограмм и получить максимальную ценность. Для этого мы начинаем с того же, как при игре в монеты: разбираем самые простые случаи, как если бы нам нужно было набрать рюкзак не на 10 килограмм, а на 2–4.
Перебирать рюкзаки начнём с такого, чтобы поместилась хотя бы одна вещь. У нас это фонарь в 2 килограмма. Значит, чтобы получить максимально ценный рюкзак вместимостью в 2, нужно положить туда фонарь. Ценность нашего рюкзака — 3.
Теперь возьмём рюкзак на 3 килограмма. У нас снова есть только одно доступное действие — в 3 килограмма поместится вода или фонарь, но ценность воды больше. Вывод: берём воду и получаем ценность 4.
Следующий шаг — собрать 4 килограмма. Это уже интереснее, потому что теперь можно выбирать, что взять: спальник, воду или два фонаря. Они в сумме дают больше всего ценности, поэтому выбираем их.
Посмотрите, что мы делаем: с каждым новым объёмом рюкзака мы решаем новую небольшую часть общего решения. При этом сохраняем результаты предыдущих задач — именно не решения целиком, а результаты, чтобы их можно было быстро использовать.
Это выглядит как таблица со всеми подсчётами: запоминаем лучшую комбинацию из вещей и ценностей и используем их для дальнейшего решения.
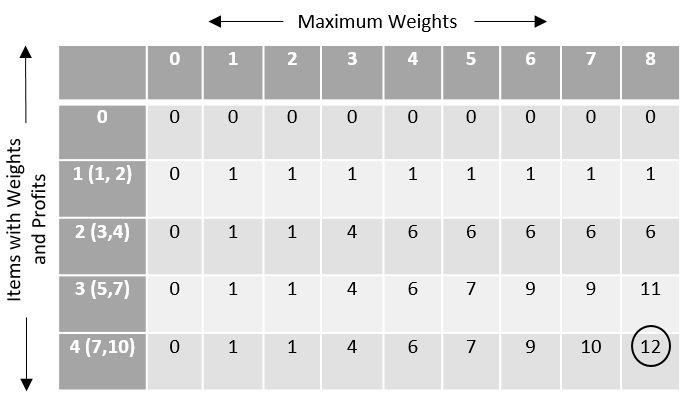
Обработка строк и выравнивание последовательностей в биоинформатике
Когда биологам нужно сравнить два фрагмента органических цепочек, на цифровом языке эти цепочки упрощённо выглядят так:
- строка 1:
ACGT. - строка 2:
AGT.
Для решения нужно понять, насколько они похожи и где именно различаются. Для этого учёные подгоняют их друг под друга и совмещают максимальное количество совпадающих фрагментов. Это называется выравниванием. Например:
A C G T
A - G T
Во второй последовательности 3 символа вместо 4, но зато эти же три символа встречаются в первой цепочке. Получается, что у нас есть одно различие и 3 совпадения.
Но может быть и другое выравнивание, которое даёт уже худший результат:
A C G T
A G - T
Проблема в том, что такие наборы значений чаще всего гораздо длиннее, разного размера и могут быть сильно не похожи по составу. Ещё их нужно сопоставить так, чтобы разницу и сходство можно было представить в виде конкретных показателей.
С динамическим программированием мы можем сравнивать элементы строк по одной и заносить результаты каждого сравнения в таблицу. Например, при совпадении элементов добавляем 1 очко, если символы разные — отнимаем, а если на месте сравнения в одной из цепочек стоит пробел, снимаем 2 очка.
В итоге мы можем построить таблицу сравнений, где зафиксируем все результаты. В таблице видно, что, если сравнить пустую вторую строку с 4 символами из первой, за каждый символ начисляется −2 очка. К последнему символу T у нас получается −8 очков.

А ещё по таблице сразу видно, что лучший результат выравнивания двух строк целиком — это 1 очко.
Экономика, финансы и оптимизация инвестиций
В экономике программирование тоже используется, но нужно помнить, что техника не может предсказать движение рынка. На стоимость ценных бумаг и положение выпустивших их компаний влияют тысячи факторов, подсчитать которые не под силу вообще никому. Зато можно предсказать риски и распределить их по портфелю инвестиций.
Динамическое программирование работает с моделью будущего, а не реальной жизнью. Поэтому можно поставить цель на несколько лет вперёд — это будет оптимальное решение задачи. Отходя с каждым шагом немного назад, компьютер может распределять капитал по вложениям разных уровней, ожидая от каждого определённую прибыль и по возможности учитывая риски.
План может быть таким:
Через 5 лет я хочу капитал в 1 000 000 рублей.
Для этого через 4 года я могу сделать вложения в облигации А и акции Б. Для этих вложений мне понадобится капитал в 800 000 рублей.
Для этого через 3 года я могу сделать вложения... И так далее.
Но в жизни такая стратегия почти наверняка не сбудется со 100-процентной точностью, и об этом нужно помнить.
Бонус для читателей
Если вам интересно погрузиться в мир ИТ и при этом немного сэкономить, держите наш промокод на курсы Практикума. Он даст вам скидку при оплате, поможет с льготной ипотекой и даст безлимит на маркетплейсах. Ладно, окей, это просто скидка, без остального, но хорошая.
Плюсы и минусы метода динамического программирования
Если посмотреть на динамическое программирование с точки зрения разработки и производительности, у этого подхода есть много выгодных сторон.
Такой метод сильно ускоряет решение задач с большим количеством данных. Для оптимизации, математики, биоинформатики, машинного обучения и некоторых других областей это большой плюс.
Динамическое программирование избавляет от повторных вычислений. Не нужно каждый раз пересчитывать данные, когда мы ищем их нужные комбинации для решения. Вместо этого у нас уже хранятся готовые ответы, которые можно использовать.
Вычисления часто можно оптимизировать дальше и хранить всего несколько строчек из ответов подзадач.
Сам факт, что динамическое программирование используется в большом количестве разных областей, говорит о его универсальности. Даже если этот подход не может использоваться во всех задачах, почти наверняка есть раздел, где пригодится решение большой задачи через дробление и упрощение.
Но минусы тоже есть.
Главная проблема в том, что это сложно. Применение динамического программирования предполагает высокий уровень абстракции, поэтому нужно время, чтобы во всём разобраться и подобрать стратегию.
Для ДП нужно правильное установление: выбрать начальную точку, понять, что именно нужно хранить из решений подзадач, и подобрать формулы перехода из более позднего состояния в предыдущее.
При работе с большими входными данными динамическое программирование будет работать долго и потреблять много памяти. Например, в задаче о рюкзаке у нас было 5 небольших значений — а с большими числами алгоритм будет работать гораздо дольше, так что применять его бесполезно.
Ещё иногда динамическое программирование просто не нужно, когда у задачи есть простое проверенное решение.
Когда в итоге стоит использовать динамическое программирование
Чтобы ответить на этот вопрос с большим пониманием, нужно разобрать этот алгоритмический метод подробнее и с примерами. Мы сделаем это в следующей статье, а пока вот краткие итоги.
Динамическое программирование полезно, если задачу можно разбить на составляющие такого же типа, как и основная задача.
Ещё важно точно знать, что принцип оптимальности Беллмана соблюдается: это когда мы знаем, что лучшее решение всей задачи состоит из лучших решений для частей.
Для быстрой работы нужно, чтобы количество и размер входных данных были разумных размеров, потому что при очень больших числах динамическое программирование не справляется.
Когда вместо динамического программирования лучше применять что-то другое:
- Если все подзадачи уникальны, хранить ответы на них бессмысленно и выгоды от динамического программирования нет.
- Обязательно нужно помнить решение целиком. В динамическом программировании хранятся только результаты, для скорости.
- Когда нужно работать с действительно большими числами, таблицы результатов подзадач получаются огромными и производительности современных компьютеров просто не хватает, чтобы получить ответ за приемлемое время. Поэтому с большими числами не годится.
Ещё иногда просто есть лучший и более быстрый алгоритм для конкретного случая. Поэтому вначале всегда нужно проверять наличие простого решения.
Частые вопросы о динамическом программировании
Как на практике определить, что задачу можно решить методом динамического программирования?
Проверьте три признака:
- задачу можно разбить на похожие подзадачи поменьше;
- решения этих подзадач повторяются, их можно использовать несколько раз;
- работает принцип оптимальности Беллмана: лучшее решение большой задачи складывается из лучших решений маленьких частей.
Если всё сходится — динамическое программирование подойдёт.
Почему динамическое программирование часто считается сложным для новичков?
Тут нужен высокий уровень абстракции — видеть не конкретные действия, а общие закономерности. Новичкам сложно определить, с чего начать разбиение задачи, что именно сохранять из результатов и как правильно переходить от одной подзадачи к другой. Плюс не всегда очевидно, что задачу вообще стоит решать через ДП, а не каким-то более простым способом. Это приходит с практикой и насмотренностью.
Всегда ли решение, найденное через динамическое программирование, будет единственно верным и оптимальным?
Нет — в обоих случаях.
Сначала про оптимальность. Чем больше подзадач, тем дольше работает алгоритм, то есть время его работы растёт в геометрической прогрессии. Есть другие алгоритмы, которые сложнее, но на больших объёмах будут работать лучше. Динамическое программирование даёт выгоду только до какого-то предела.
Единственным — тоже нет. Может быть несколько разных комбинаций действий, которые дают одинаково хороший результат. Например, в задаче о рюкзаке могут существовать два набора предметов с одинаковой итоговой ценностью. ДП найдёт оптимальное значение, но не гарантирует уникальность пути к нему.
Какие основные ограничения у динамического программирования по памяти и как с ними борются?
Главная проблема — таблицы с результатами подзадач быстро разрастаются и съедают много памяти. При работе с большими входными данными или многомерными задачами память может закончиться раньше, чем компьютер найдёт ответ. Бороться с этим можно так: хранить не всю таблицу, а только несколько последних строк или столбцов, которые нужны для текущих вычислений. Ещё помогает оптимизация структуры данных — использовать хеш-таблицы вместо массивов или сжимать данные.
С чего лучше начать изучение динамического программирования на практике?
Начните с классических простых задач. Сначала решите их обычным перебором, чтобы понять логику. Потом попробуйте переписать через динамическое программирование и сравните скорость работы. Когда освоитесь с базой, переходите к задачам на строки и последовательности — там уже интереснее и ближе к реальной практике.
Ищете работу в IT?
Карьерный навигатор Практикума разберёт ваше резюме, проложит маршрут к первому работодателю, подготовит к собеседованиям в 2026 году, а с января начнёт подбирать вакансии именно под вас.