Кому интересен анализ данных — эта статья для вас.
Для этой статьи мы обратились к учебникам по эконометрике Я. Р. Магнуса, П. Л. Катышева и А. А. Пересецкого. Будет нудно, но простыми словами. Крепитесь.
Введение про работу эконометриста
В программировании есть термин reverse engineering, или обратная разработка. Например, вы делаете какое-то приложение, и руководитель показывает продукт конкурентов и говорит: «Надо сделать так же». Вы внимательно изучаете то, как работает программа, смотрите на финальный машинный код и пытаетесь сделать что-то похожее. В общих чертах это и есть обратная разработка.
Работа эконометриста примерно похожа на обратную разработку. Например, нам нужно проанализировать, от чего зависит зарплата сотрудника. Мы собираем данные по зарплатам, опыту работы, размеру компании, необходимым навыкам и применяем нужные методы анализа данных к датасету. Если всё хорошо, то на выходе мы сможем сказать, кому и за что платят какие суммы.
Цель эконометриста — это не само получение данных, а их интерпретация и понимание, как именно эти данные были получены. Эконометрист берёт датасет и пытается восстановить логику, почему в данных появились именно такие взаимосвязи и именно такие выводы.
При чём тут эконометрические модели
Возьмём датасет из предыдущей статьи по эконометрике.
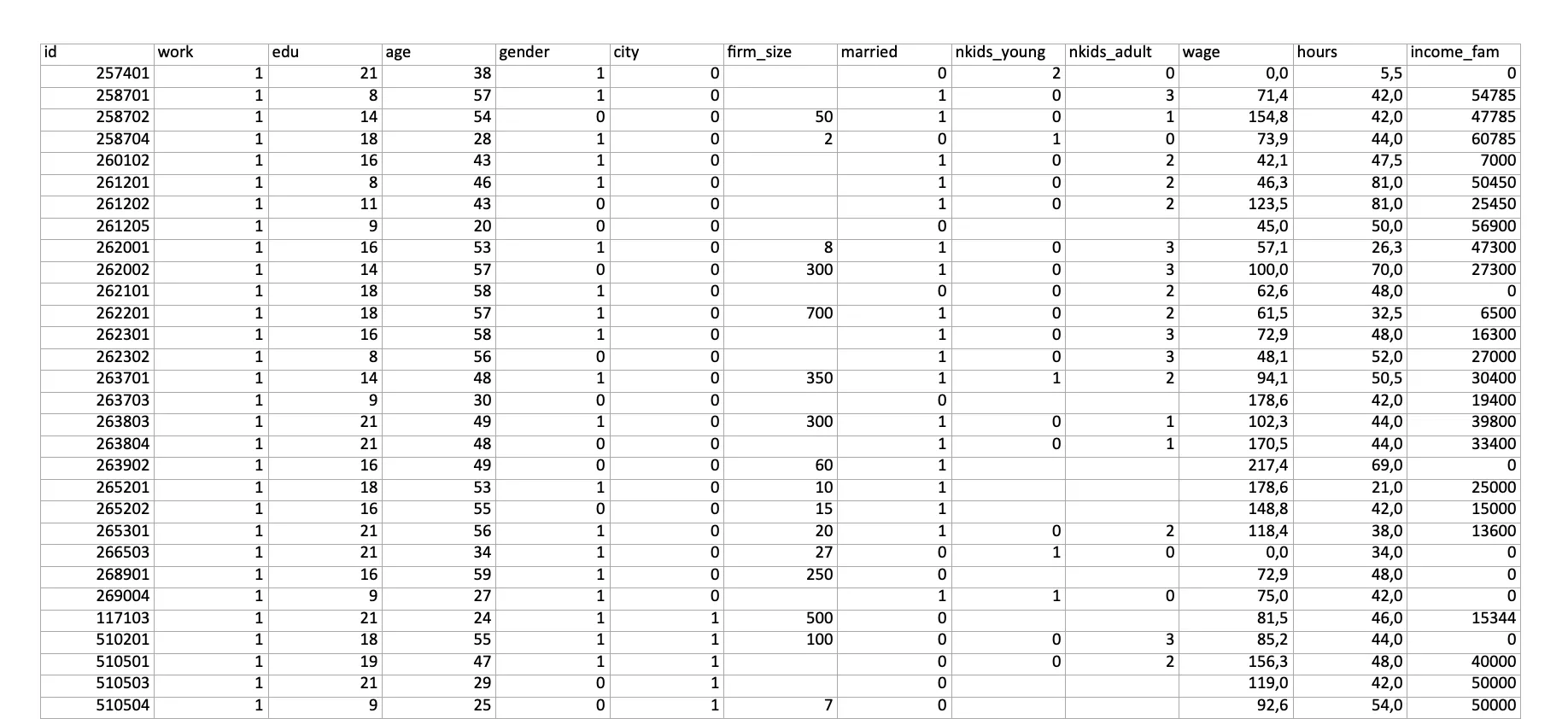
Напомним условия: аналитик в компании получил задание проанализировать таблицу с данными. Проводился опрос среди населения, в ходе которого собирали данные: пол, возраст, уровень образования, наличие детей, какая зарплата и сколько часов работает. Всего получилось 6 183 наблюдения.
Эти наблюдения — только инструмент, который помогает ответить на интересующие вопросы. Например, как влияет пол на размер зарплаты; есть ли связь между возрастом, наличием детей и размером зарплаты, между уровнем образования, количеством отработанных часов и почасовой зарплатой.
Аналитик понимает, что зарплаты в экономике формируются в соответствии с определёнными закономерностями.
Модель — это выраженная в математическом виде экономическая закономерность, которая принимает вид уравнения. Внутри уравнения есть зависимая анализируемая переменная (y), независимая (x) и шум (ε).
В математическом виде модель может выглядеть как-то так:

Какие модели могут быть — на примере нашего датасета
Представим, что мы исследуем взаимосвязь количества отработанных часов и размера зарплаты. Задача — понять, влияет ли количество отработанных часов на размер зарплаты; если влияет — то на сколько процентов изменится зарплата, если увеличить количество отработанных часов на 1%.
Проверяем, не случайны ли данные и нет ли такого, что данные никак не связаны друг с другом. Для этого включаем генератор чисел и генерируем 6 183 случайных наблюдения. Математически получается такая модель:
ln(wage) = 𝛽0 + 𝜀
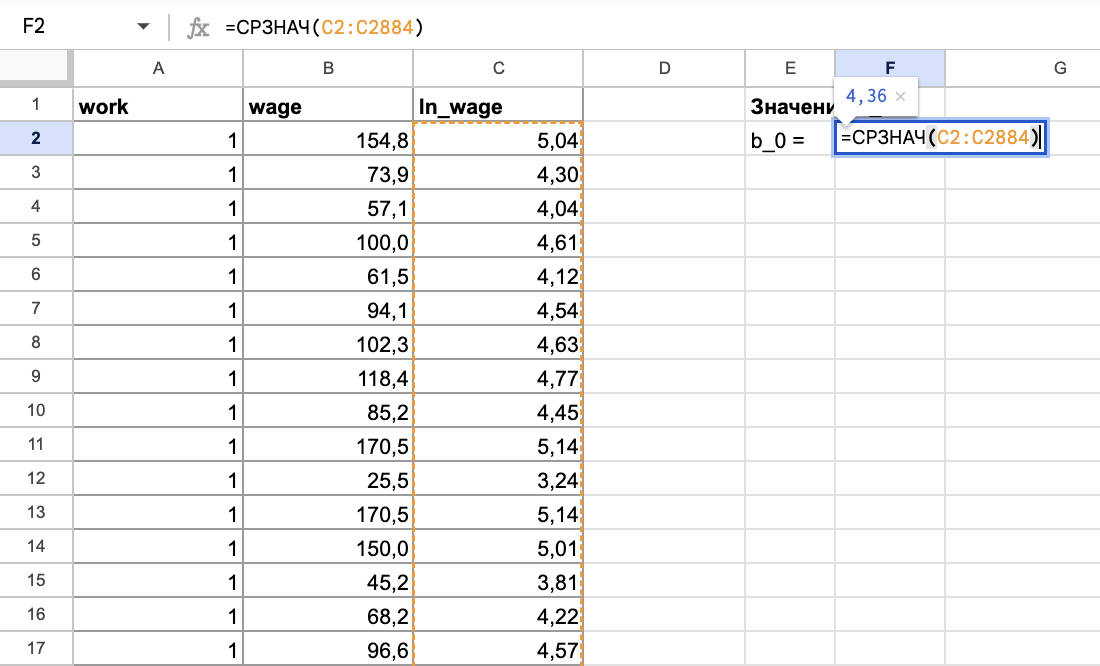
Переменные в данной модели не зависят друг от друга. Здесь мы не сможем увидеть никаких закономерностей ни в таблице, ни на графике. Единственное, можно найти значение b_0 — оно будет равно 4,36. Уравнение решено.
Предполагаем, что в нашем датасете наблюдается какая-то зависимость — значит, модель будет другая. Например, такая:
ln(wage) = 𝛽0 + 𝛽1ln(hours) + 𝜀
В этом уравнении зарплата (ln(wage)) — независимая переменная, часы (ln(hours)) — зависимая. Теперь другое дело: если генерировать данные по такой модели, то в данных будет наблюдаться зависимость зарплаты от отработанных часов — а это уже близко к реальным данным.
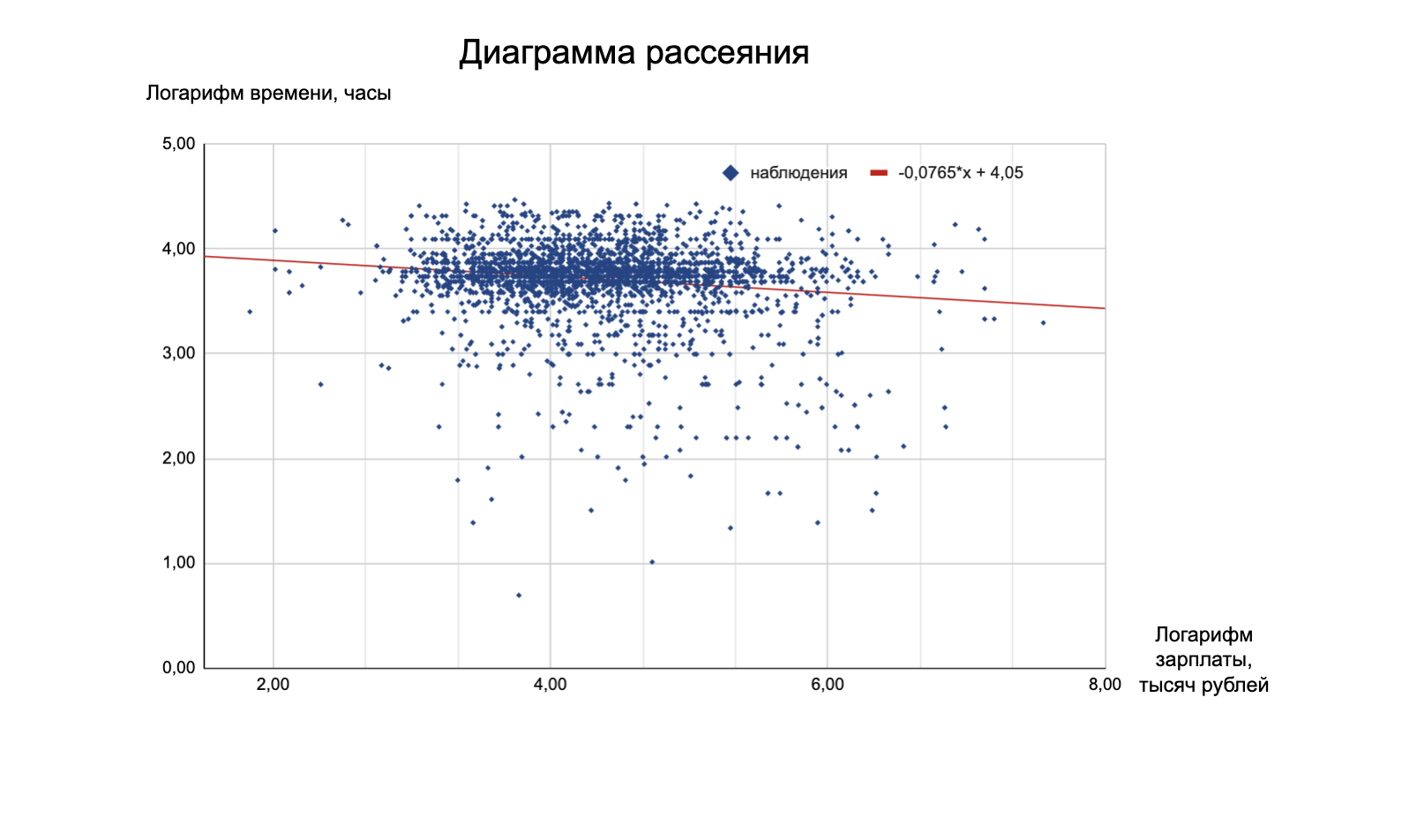
При увеличении количества часов на 1% зарплата уменьшается на 0,07%. Такой вывод можно сделать только для этой модели и только для наших исходных данных. Кому интересно: все расчёты можно посмотреть в таблице.
Но ведь у нас большой массив данных — мы можем включить в модель какие-то ещё переменные. Например, важно учесть пол и город проживания опрашиваемых. Кажется, что пол и место жительства могут повлиять на размер зарплаты.
Гипотеза такая: скорее всего, женщины зарабатывают меньше мужчин, а зарплаты в большом городе выше, чем в сельской местности.
Включаем две новые переменные в модель:
ln(wage) = 𝛽0 + 𝛽1ln(hours) + 𝛽2(gender) + 𝛽3(city) + 𝜀
Если city в таблице принимает значение 0 — значит, человек живёт в сельской местности, 1 — в большом городе. Если gender принимает значение 0 — это мужчина, 1 — женщина. Далее строим новую регрессию с новыми переменными и получаем какие-то новые значения — пока не важно какие.
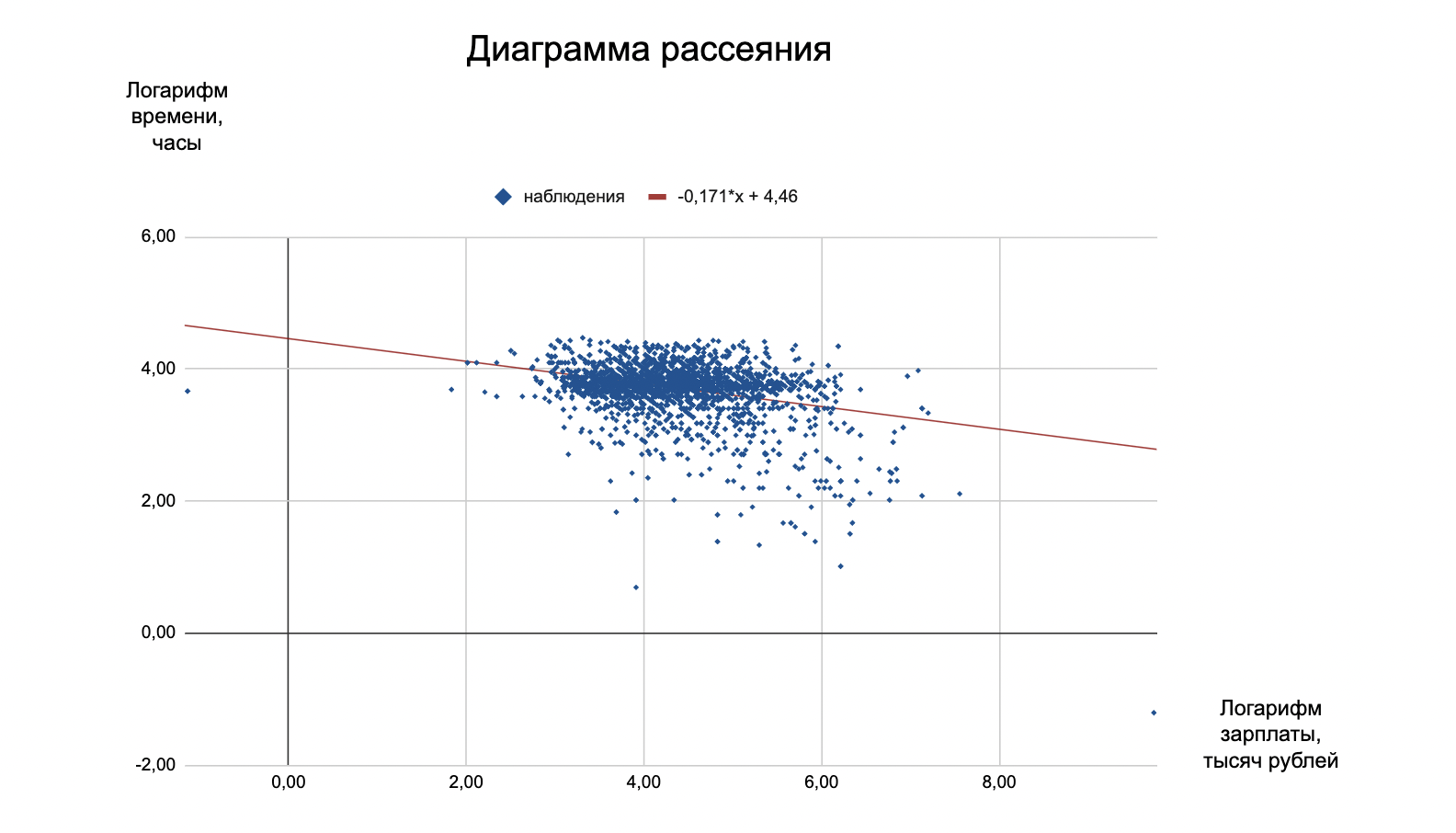
В данной модели мы можем сделать дополнительные выводы. Например, что у женщин зарплаты на 15,6% ниже, чем у мужчин. Но этого по графику с одним трендом мы не увидим, нужно смотреть на расчёты.
Теперь мы ещё на шаг ближе к реальности — сгенерированные по такой модели данные будут больше напоминать настоящие данные, в которых зарплата зависит от места жительства и пола.
Когда мы строим модели, мы постепенно восстанавливаем процесс и начинаем понимать, какие закономерности здесь работают.
Моделей может быть бесконечно много
Если бы мы пошли ещё дальше, то можно было бы оценить, какие переменные и каким образом влияют на производительность труда; как связаны размер фирмы, количество детей и размер зарплаты.
Как только в уравнении появляется новая переменная — перед нами новая модель, в которой мы получим какие-то новые значения, отличные от всех других моделей.
Как понять, какие переменные нужно включить в анализ, а какие нет?
Здесь мы спросили опытного эконометриста — читайте его ответ:
«Сложный вопрос. Если нам нужно понять, как одна переменная влияет на другую, то как минимум эти две переменные точно нужно включить. А вообще нужно попытаться представить, что происходит в жизни и какие закономерности действовали, когда возникали эти данные. Здесь поможет здравый смысл. Например, если нам кажется, что зарплата зависит от опыта работы, то это хороший повод включить опыт работы в модель. При этом может случиться так, что опыт совсем не влияет на зарплату — это нормально, модель нас проверила и поправила. Так что можно включать в модель и те переменные, в которых мы сомневаемся.
Есть ещё некоторые технические нюансы:
— Не стоит включать переменные, которые не только влияют на зависимую переменную, но и сильно связаны между собой. Например, часто не получится включить в модель одновременно возраст, опыт работы и продолжительность обучения человека. Если люди начинают учиться в одном возрасте, а к работе приступают примерно с окончанием обучения, то, скорее всего, опыт плюс длительность обучения примерно дадут возраст. В этом случае по моделям будет тяжело разобраться, то ли это возраст влияет, то ли опыт работы.
— Не получится включить переменные, которые не меняются. Если переменные не меняются, то это и не переменные, верно?
— Если в простой модели получается слабая связь между двумя переменными, возможно, нужно включить новые переменные или подумать о логичности поиска взаимосвязей между выбранными переменными».