Что общего у игральных кубиков и нормального распределения

Сегодня посмотрим на практике, как работает закон нормального распределения. Если пропустили первую часть с теорией, вот короткая версия:

А вот как выглядит график нормального распределения:

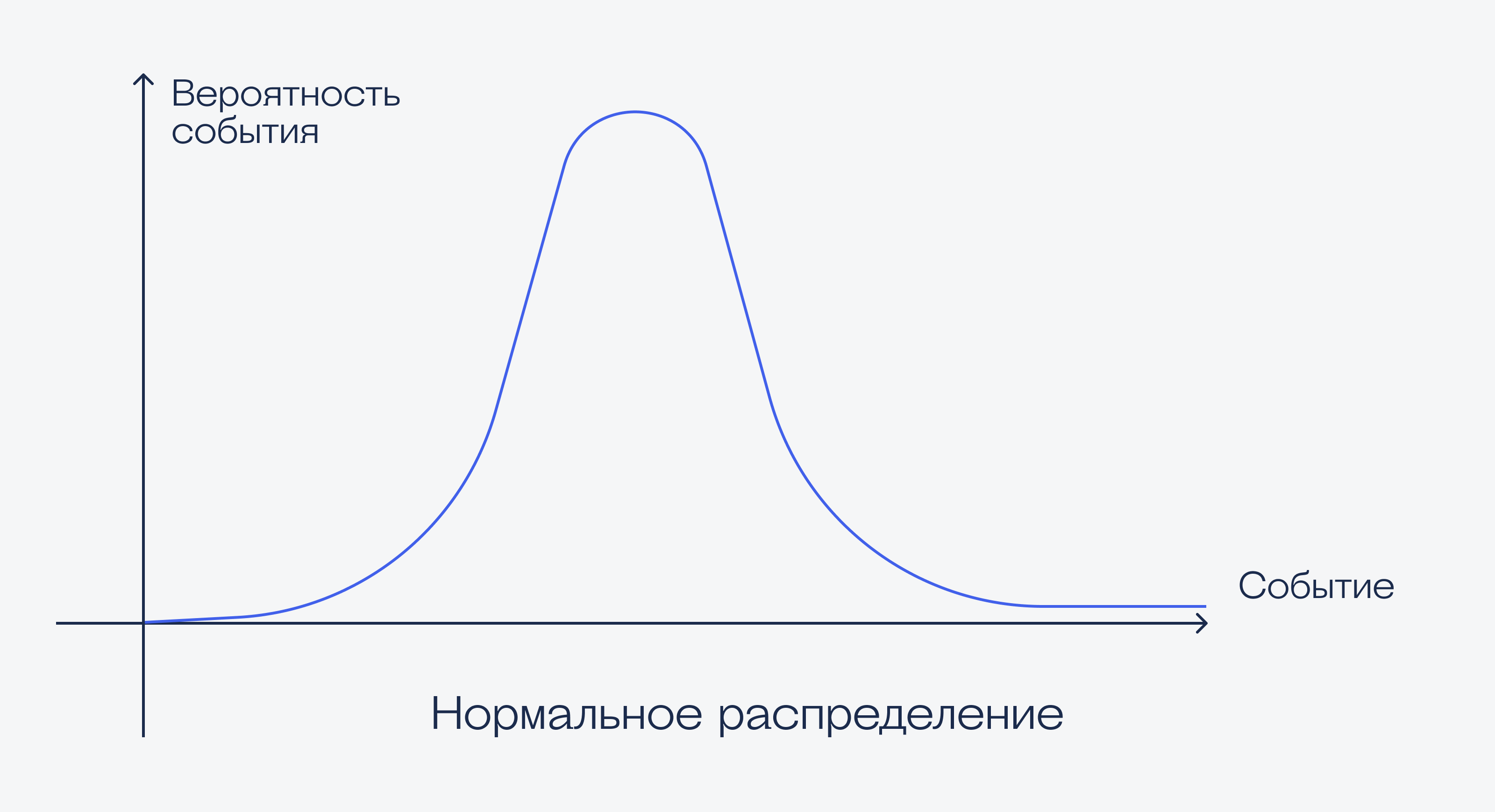
Что делаем

Мы проверим этот закон в деле — действительно ли события распределяются именно таким образом и что влияет на форму графика. Для этого мы будем использовать игральные кубики — те, на которых стоят точки или цифры от 1 до 6.

В теории, если у нас будет два кубика, то вот какие есть варианты их совместного выпадения:

Теперь, если мы сложим значения каждой пары и распределим их по количеству таких значений, то получим такую картину:

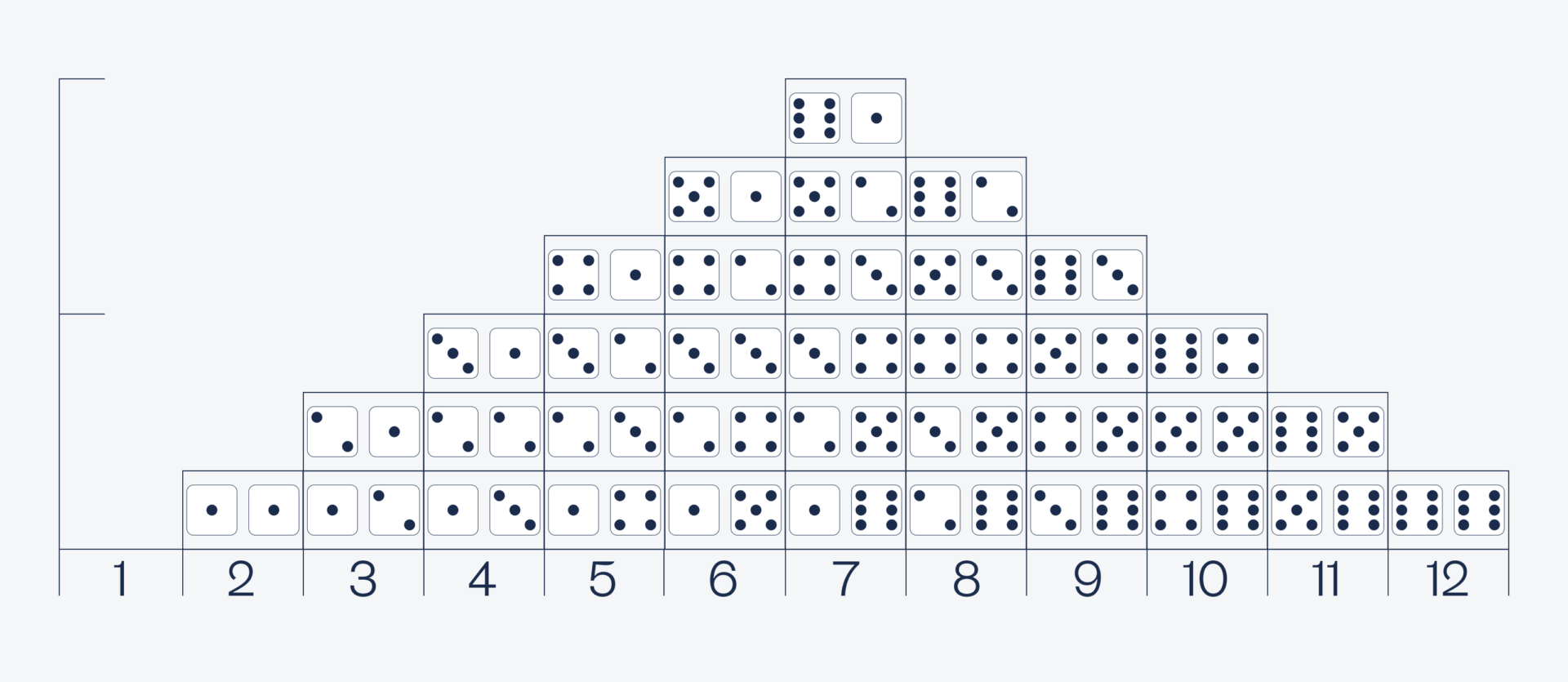
Здесь единицу не даёт ни одна сумма, двойку можно получить только парой 1—1, тройку — уже двумя парами 1—2 и 2—1 и так далее. Это немного похоже на кривую Гаусса, но слишком ровную, без явного пика и спадов. 

Мы будем подкидывать кубики много раз, складывать их значения и строить графики, чтобы посмотреть, как количество кубиков влияет на форму графика. Начнём с двух кубиков и постепенно дойдём до десяти.

Если знаете английский, посмотрите это видео — в нём будет всё то же самое, только с красивой анимацией и сложными формулами. Старт уже стоит на нужном таймкоде:

Бросаем два кубика

Логика будет такой: мы бросим кубики сто раз, на каждом броске посмотрим на сумму и в итоговом списке увеличим на единицу значение, которое соответствует сумме. Поясним на примере:

При этом у нас нулевой и первый элемент итогового списка всегда будет равен нулю. Это из-за того, что два кубика не могут дать в сумме ни ноль, ни единицу. Значит, нам нужно исключить их из списка, перед тем как строить график.

Запишем это на Python. Чтобы было понятнее, прокомментировали каждую строчку кода:

# подключаем модуль для построения графиков
from matplotlib import pyplot as plt   
# и модуль случайных чисел
import random

# список с результатами, на старте нулевой
result = [0] * 13
# диапазон возможных сумм
x = list(range(2, 13))

# бросаем кубик нужное число раз
for i in range(100):
    # получаем значение броска каждого кубика
    dice1 = random.randint(1, 6)
    dice2 = random.randint(1, 6)
    # складываем значения
    summ = dice1 + dice2
    # увеличиваем на единицу соответствующее значение списка с результатами
    result[summ] += 1

# убираем нулевой и первый значения списка — в них ничего нет
result.pop(0)
result.pop(0)
# формируем график
plt.plot(x,result)   
# подписываем оси
plt.ylabel('Сколько раз выпало')   
plt.xlabel('Сумма бросков')   
# показываем график в отдельном окне
plt.show()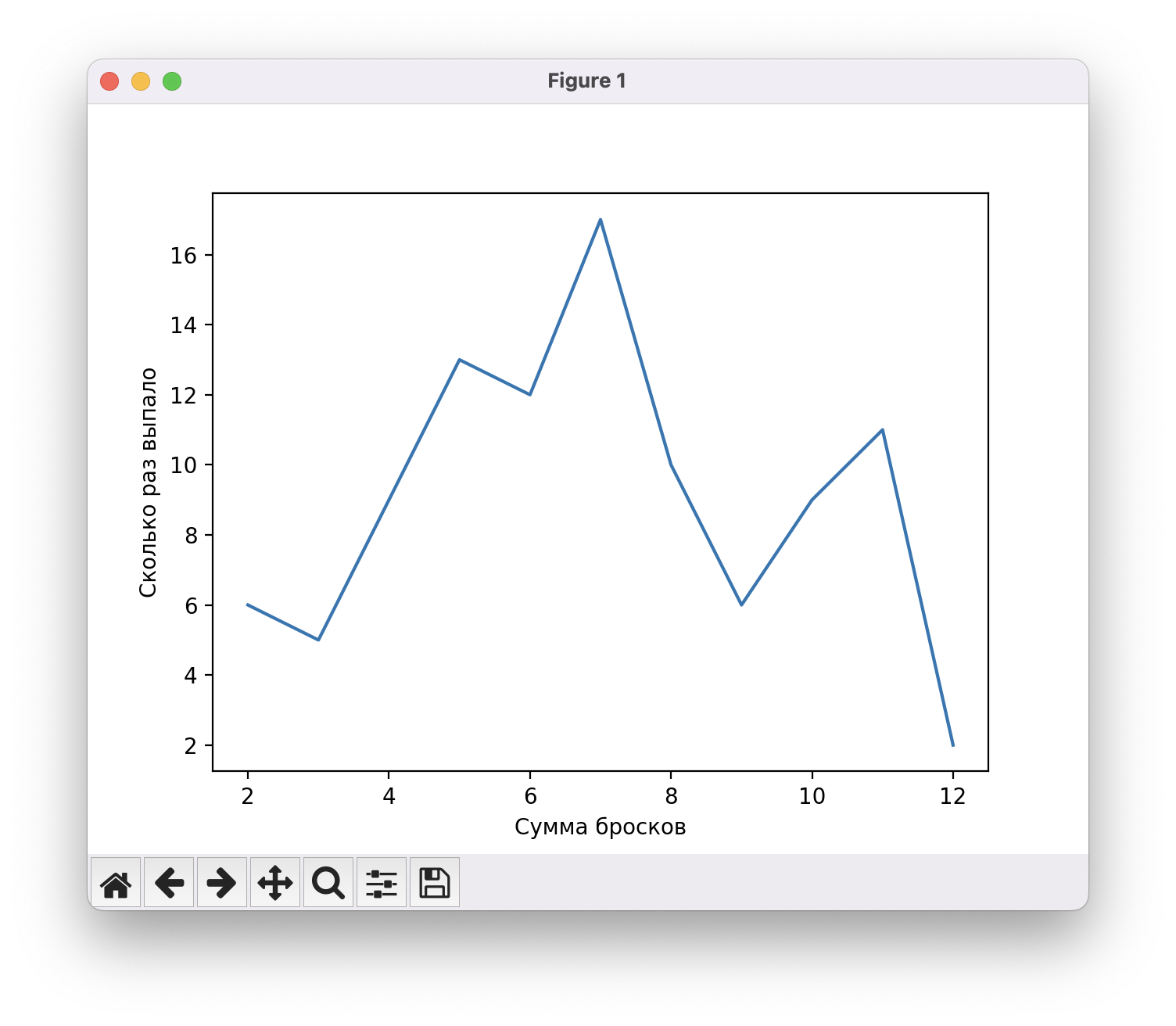 

График выглядит не так, как мы ожидали — он совсем не похож на график нормального распределения. Дело в маленьком количестве бросков — результаты просто не успевают распределиться в нужных пропорциях.

Увеличим количество бросков до тысячи:

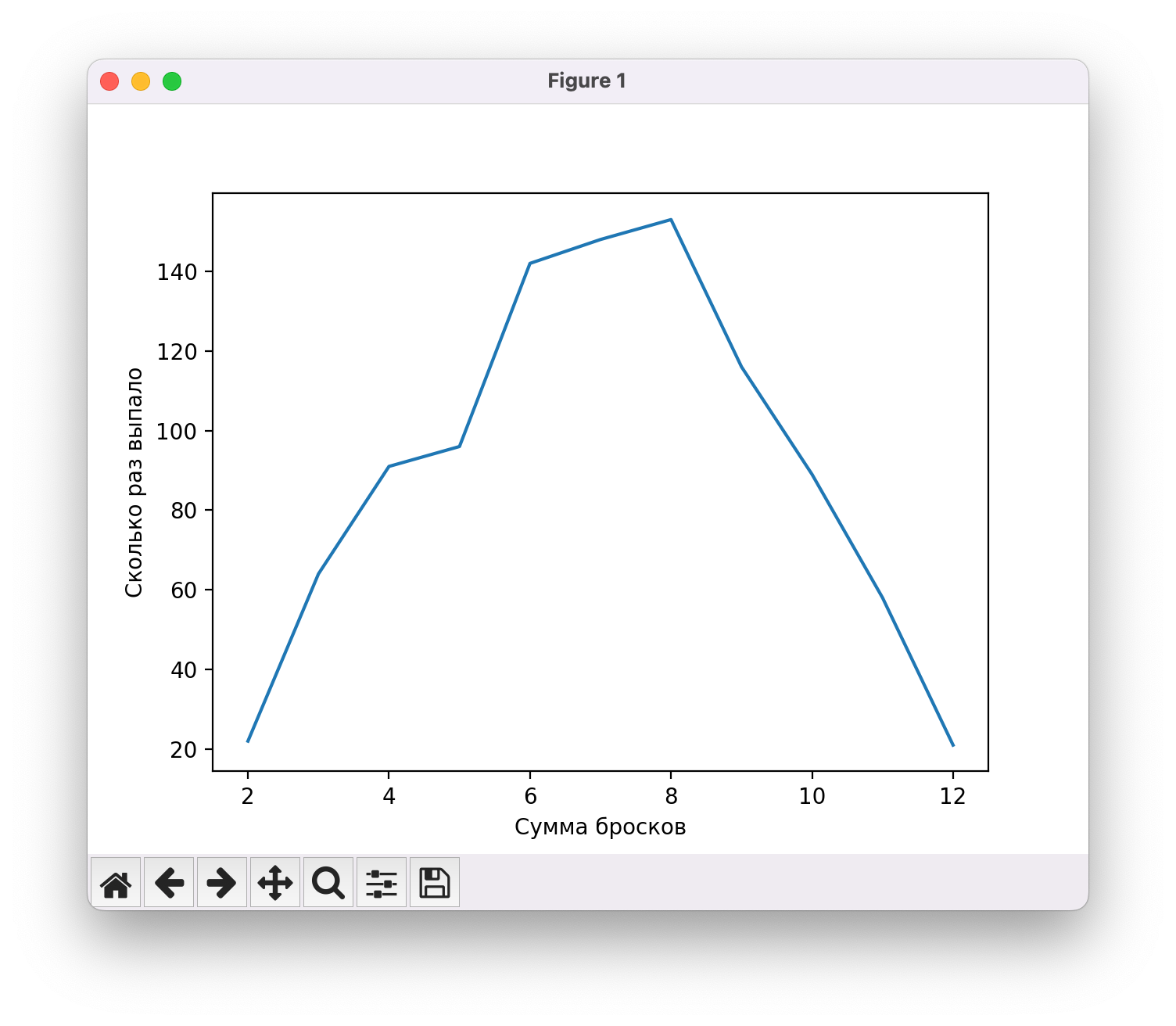
Мы увеличили количество бросков, но что, если при этом ещё увеличить количество кубиков? Давайте посмотрим на графики, где мы бросаем 3, 5 и 10 кубиков. А заодно увеличим количество бросков в 10 раз.

Вам может быть интересно:

Теория игр: самое начало, без которого дальше будет сложноЧто такое нормальное распределение и как оно предсказывает будущееКрутой веб-проект: симуляция нормального распределения на JavaScriptРаспределение Парето: все знают, мало кто применяетСчитаем деньги правильно: продвинутый Эксель и принцип ПаретоКак теория игр работает на практике и помогает выигрыватьПишем игру Ним на PythonДелаем непобедимую игру Ним

Три кубика

Прежде чем собирать код для трёх кубиков, исправим недочёты предыдущего скрипта. Для двух кубиков он пойдёт, но если надо больше — придётся переписать часть кода.

Прежде всего нам будет нужна переменная, которая отвечает за количество кубиков:

dice = 3

Раз у нас изменилось количество кубиков, соответственно, изменилась и минимальная, и максимальная сумма очков при каждом броске. Нижняя граница, кстати, совпадает с количеством кубиков (три кубика — минимальная сумма равна трём):

# минимальная и максимальная сумма очков при каждом броске
low = dice
high = dice * 6

Ещё нужно учесть количество кубиков при каждом броске, чтобы получить точную сумму, и удалить нужное количество нулевых элементов итогового списка. Например, при трёх кубиках нужно удалить четыре первых элемента.

Перепишем код, учитывая новые вводные:

# подключаем модуль для построения графиков
from matplotlib import pyplot as plt   
# и модуль случайных чисел
import random

# количество кубиков
dice = 3
# минимальная и максимальная сумма очков при каждом броске
low = dice
high = dice * 6
# количество бросков
roll = 1000

# список с результатами, на старте нулевой
# количество элементов — на один больше максимальной суммы
result = [0] * (high + 1)
# диапазон возможных сумм
x = list(range(low, high))

# бросаем кубик нужное число раз
for i in range(roll):
    # перед каждым броском общая сумма равна нулю
    summ = 0
    # кидаем по очереди все кубики
    for i in range(dice):
        # складываем значения каждого кубика
        summ += random.randint(1, 6)
    # увеличиваем на единицу соответствующее значение списка с результатами
    result[summ] += 1

# убираем все ненужные значения списка — в них ничего нет
for i in range(dice+1):
    result.pop(0)
# формируем график
plt.plot(x,result)   
# подписываем оси
plt.ylabel('Сколько раз выпало')   
plt.xlabel('Сумма бросков')   
# показываем график в отдельном окне
plt.show()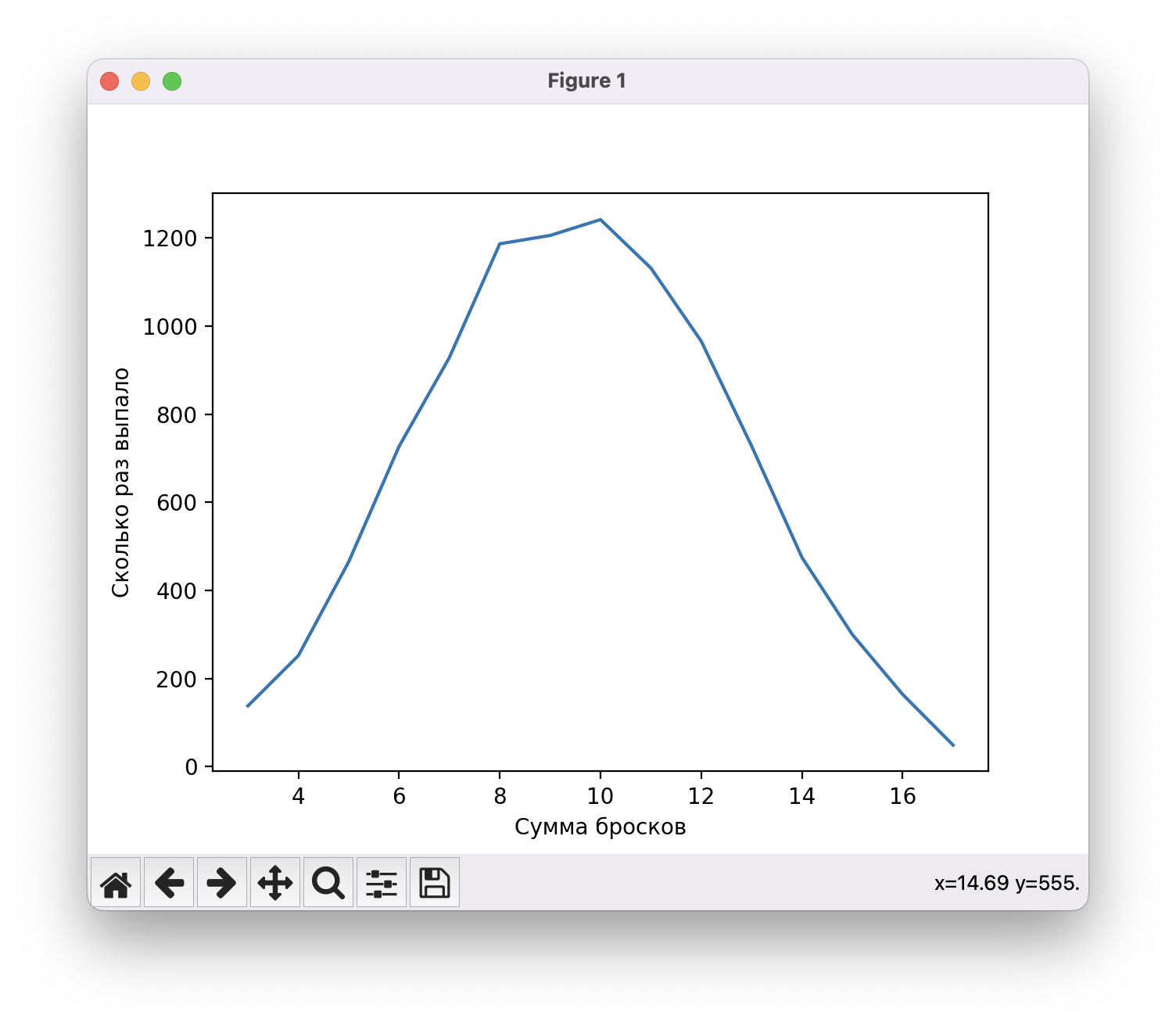

Похоже на предыдущий график с двумя кубиками. Посмотрим, что будет при пяти и десяти кубиках.

Пять кубиков

Поставим в переменную dice значение 5. График немного сгладился, потому что вариантов суммы стало больше:

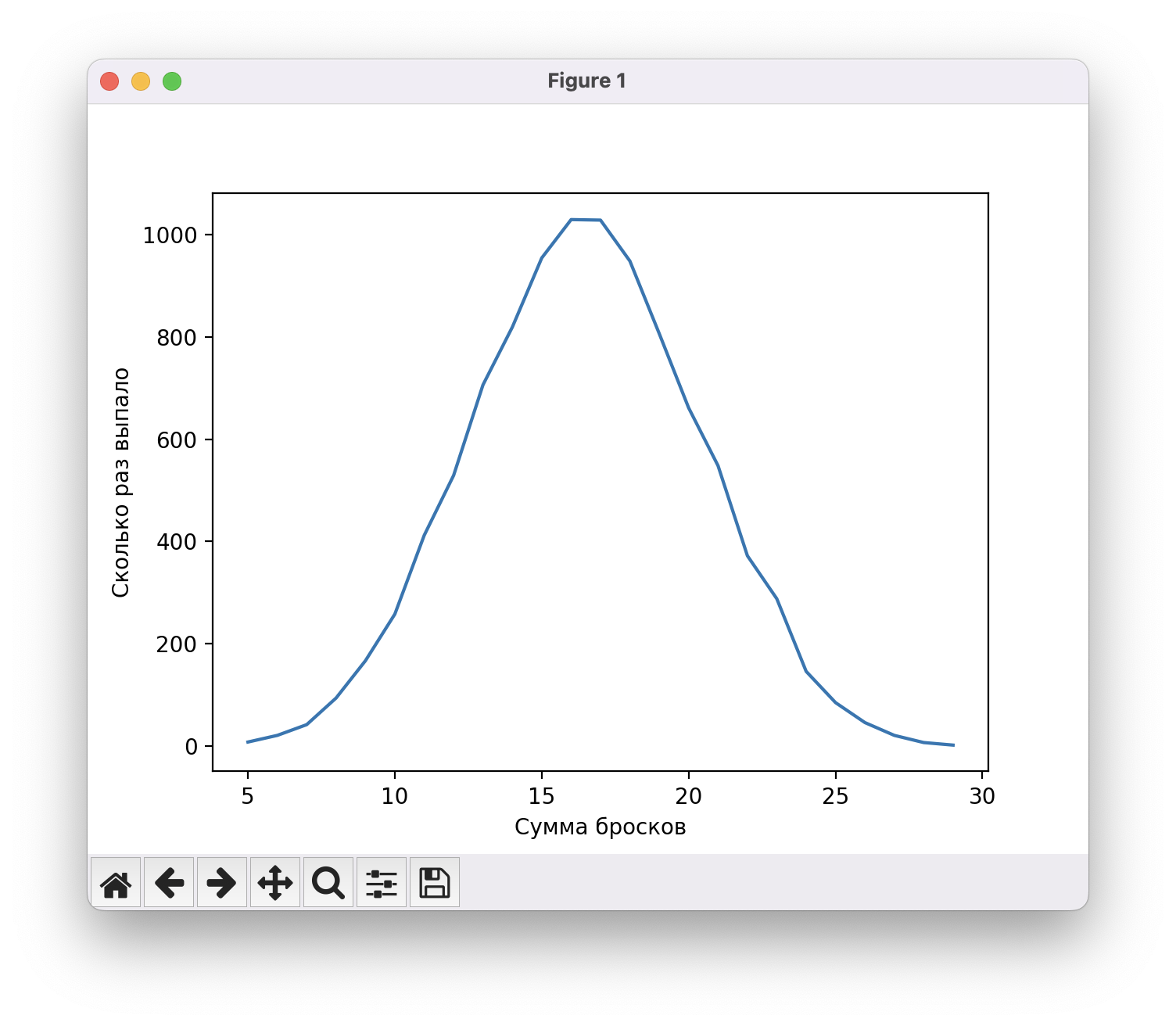
Десять кубиков

Наконец, поставим в переменную dice значение 10. Вот теперь график похож на классическую кривую Гаусса. Получается, что всё дело в количестве — чем больше данных, тем точнее работает закон распределения.

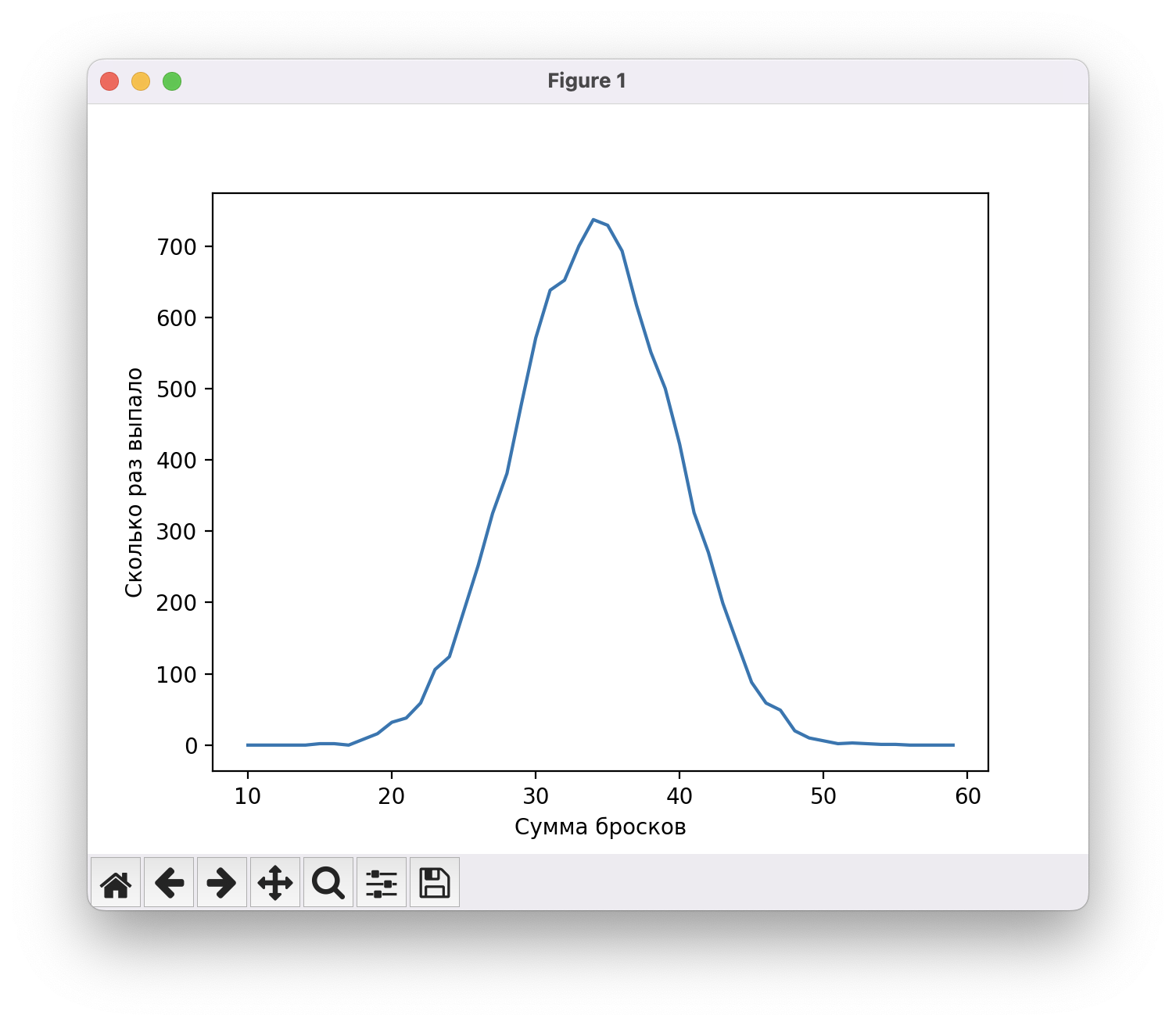
Бонус

А вот как выглядит 100 кубиков и миллион бросков:

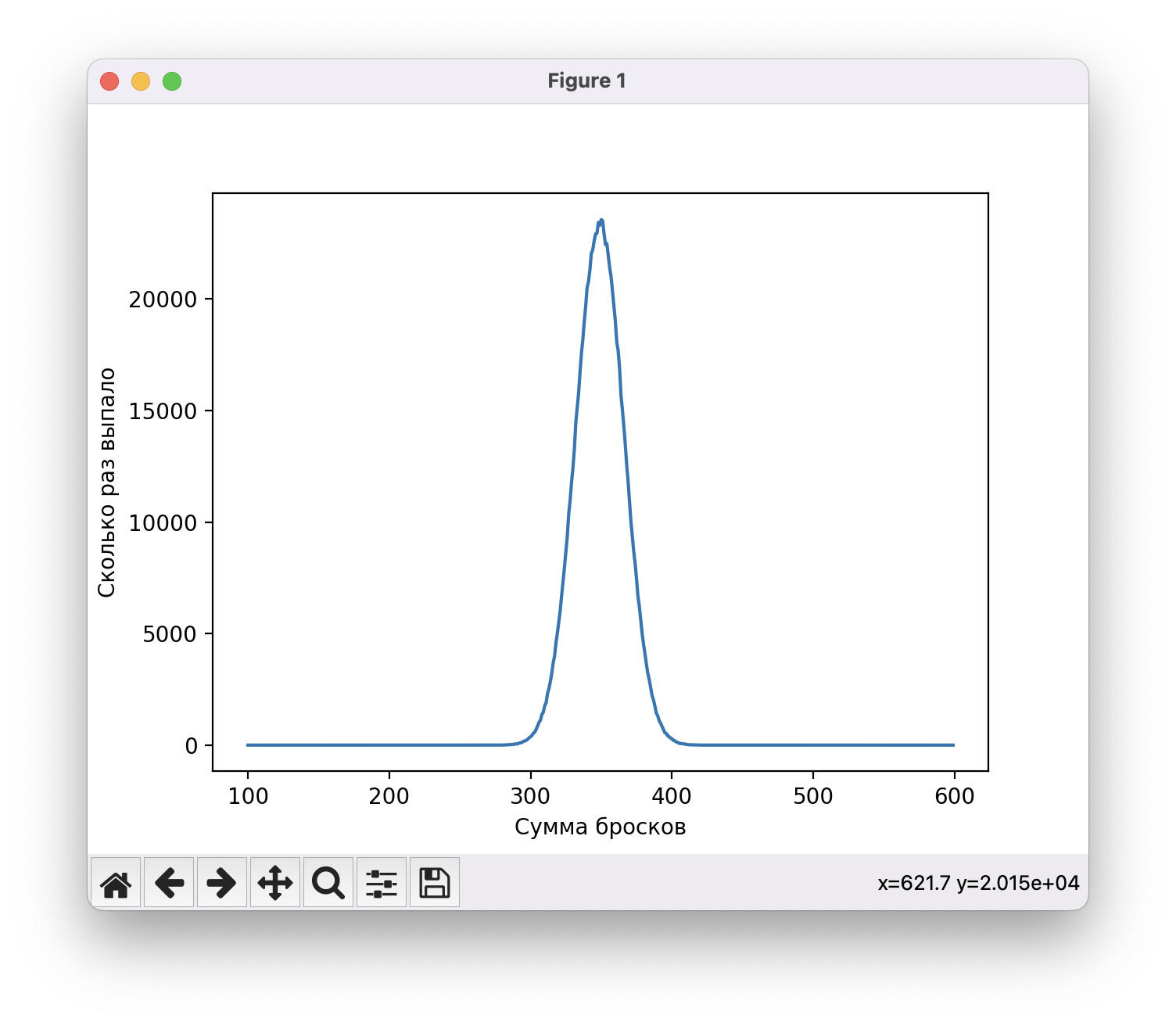
И что в итоге

Мы на практике убедились, что закон нормального распределения работает даже в бросках кубиков. При этом чем больше кубиков и больше бросков — тем точнее работает закон. Это значит, что на небольшом количестве данных этот закон применить не получится — всё испортит слишком большая погрешность. Но если данных много, то влияние погрешности будет уже не таким большим и можно будет на основе данных делать нужные выводы.

Ещё видно, что количество бросков тоже играет роль — чем их больше, тем сильнее выделяется середина графика, где значения суммы встречаются чаще всего.

Данные — это новая нефть

А аналитики данных — новая элита ИТ. Эти люди помогают понять огромные массивы данных и принять правильные решения. Изучите профессию аналитика и начните карьеру в ИТ: старт — бесплатно, а после обучения — помощь с трудоустройством.

Качать бесплатно