Если у вас есть игральный кубик и вы бросите его один раз, никто не может предугадать, что на нём выпадет. Но если бросить этот же кубик 10 тысяч раз, выпавшие числа можно будет предсказать почти безошибочно. Это возможно благодаря неочевидным законам статистики, в частности — благодаря нормальному распределению.
В этой статье объясняем, что такое нормальное распределение и зачем оно нужно. Зная о законе нормального распределения, вы сможете предсказывать будущее, понимать любые социальные процессы и не вестись на манипуляции журналистов. Ну и просто прокачаетесь в математике.
Короткая версия статьи
- Закон нормального распределения — это статистический закон, который описывает большие наборы данных — например 10 тысяч бросков кубика.
- Закон говорит: есть среднее значение, оно встречается чаще всего; чем дальше от среднего — тем реже оно встречается.
- Нормальное распределение представляют в виде графика, который похож на плавную кривую (как холм такая).
- Закон нормального распределения работает почти во всех областях, где происходят случайные события: от игральных костей до макроэкономических процессов.
— Объясни смысл закона нормального распределения гуманитарию.
— Конечно! Закон нормального распределения — это математический закон, который показывает, как распределяются случайные величины. В простых словах, он описывает, как часто происходят события в определённом диапазоне значений.
Давайте представим, что мы измеряем рост студентов в классе. Если мы построим график, показывающий, как часто встречаются разные значения роста, то мы увидим, что большинство студентов имеют средний рост, а те, кто имеют очень низкий или очень высокий рост, встречаются гораздо реже. Это и есть закон нормального распределения.
Для гуманитария это означает, что мы можем использовать математические законы для описания различных явлений в мире, даже если мы не работаем с числами. Например, мы можем использовать закон нормального распределения, чтобы понять, как распределяются оценки студентов по разным предметам или как распределяется доход населения в определённой стране.
Что такое распределение
Распределение — это когда мы берём все данные и раскладываем их по какому-то выбранному значению.
Например, мы можем взять все цены «Пятёрочки» и нанести их на линию: от низких до высоких.
Часто при распределении данных много значений оказываются сгруппированы плотнее, а совсем немного значений стоят по краям. Или почти всё сгруппировано слева, а справа возникает длинный хвост из значений, которые встречаются сильно реже других. Законы распределения как раз описывают, как будут распределяться данные при разных входных параметрах.
Что такое нормальное распределение
Закон нормального распределения — это статистический закон, который описывает, как часто различные значения случайной величины встречаются в наборе данных. Он также известен как «закон Гаусса», или «закон распределения Гаусса».
Если сформулировать суть закона распределения Гаусса, то она будет звучать примерно так:
значения случайной величины будут сгруппированы вокруг среднего значения, и чем дальше от среднего значения, тем меньше вероятность того, что такое значение появится.
Разберём это по полочкам:
- Есть массив данных, полученных от какого-то хаотичного процесса.
- Есть некое среднее значение в этом массиве данных.
- Вот этого среднего будет больше всего.
- Чуть дальше от среднего — будет поменьше значений.
- Ещё дальше — ещё меньше.
- Каких-то экстремальных значений будет крайне мало.
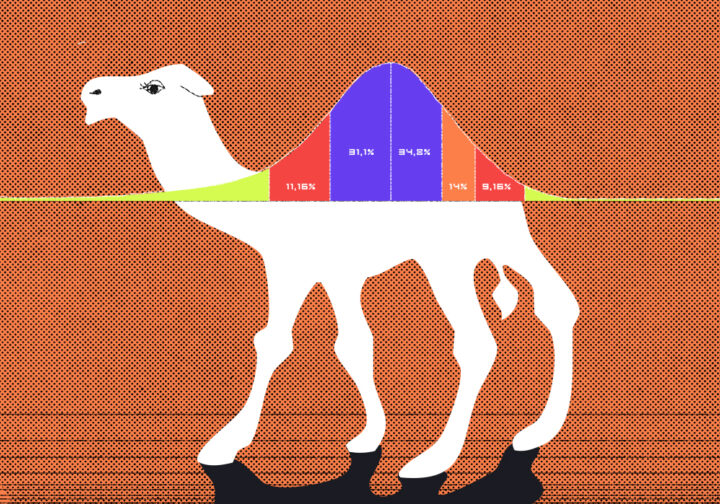
Если нарисовать это распределение в общем виде, получится график в форме колокола. В центре колокола — среднее значение, а по краям — отдалённое от среднего:
Допустим, мы работаем в бухгалтерии крупной компании — на 10 тысяч человек. Нам стало интересно, как распределяются размеры зарплат. Для этого мы выгружаем данные в Эксель и пишем там формулу, которая посчитает, сколько зарплат входит в каждый диапазон с шагом в 5000 рублей.
Мы увидим, что сто человек получают 10 тысяч рублей, около тысячи работников получает 20–30 тысяч, большинство получает 40–60, несколько десятков получает 90, какие-то единицы будут получать больше 90.
А теперь самое интересное — график такой формы мы получим почти в любой компании (без привязки к конкретным цифрам, речь про форму). Причём чем больше будет в ней сотрудников, тем ближе будет результат к идеальному графику нормального распределения.
В названии закона слово «нормальное» означает то, что в данных нет сильного отклонения от средних значений, которое принимается за норму. Это не значит, что есть «нормальное», а есть «ненормальное» распределение — это просто название закона.
— Приведи примеры, где используется закон нормального распределения.
— Закон нормального распределения используется во многих областях, например:
1. Статистика: для анализа данных, таких как оценки студентов, доходы населения, рост и вес людей, продолжительность жизни и т. д.
2. Финансы: для прогнозирования цен на акции и другие финансовые инструменты, оценки рисков инвестирования и т. д.
3. Производство: для контроля качества продукции, определения стандартных значений параметров, таких как длина, ширина, высота и т. д.
4. Медицина: для изучения здоровья населения, например для определения среднего роста и веса людей в разных возрастных группах, для определения нормальных уровней кровяного давления, холестерина, глюкозы и т. д.
5. Инженерия: для проектирования и тестирования различных устройств и систем, например для определения среднего времени работы механизма до отказа, для определения стандартных значений температуры, влажности и т. д.
Это лишь несколько примеров, где используется закон нормального распределения. В общем, он находит применение во многих научных и практических областях, где требуется анализ и интерпретация данных.
В чём польза от такого закона
Знание этого закона позволяет предсказать, насколько вероятно встретиться с какой-то величиной в горе случайных значений.
Например, у вас есть список инвесторов некой инвестплатформы. Вы можете отсортировать его по величине дохода, и вы увидите в начале таблицы самых успешных инвесторов. Это экстремальное значение:
А если теперь построить распределение всех инвесторов на платформе, картина будет другой: единицы зарабатывают много, а в основном люди зарабатывают 1–3%, что сопоставимо с банковским вкладом:
Пример: оптимизация софта
Допустим, мы пишем программу для портных. В ней есть функция, которая требует больших вычислений, — например форма лекала брюк в зависимости от роста человека.
Нам известно, что функция имеет распределение близкое к нормальному: есть некий средний рост людей, он встречается чаще всего.
Мы можем заранее просчитать наиболее частые значения этой функции, чтобы она не высчитывала лекала каждый раз с нуля, а доставала готовые значения. Так программа будет работать намного быстрее.
Какие ещё бывают распределения
Кроме нормального распределения есть ещё много других распределений, например:
- дискретное равномерное,
- геометрическое,
- распределение Бернулли,
- экспоненциальное,
- равномерное непрерывное,
- распределение Коши,
- хи-квадрат,
- распределение Парето.
Все они используются для решения разных задач, как-нибудь доберёмся и до них.
О чём мы ещё не рассказали
Сложно за один присест рассказать про всё, что связано с нормальным распределением, — статья получится неподъёмной. Например, вот что осталось за кадром:
- простая демонстрация закона нормального распределения на примере игральных кубиков;
- доска Гальтона и распределение шариков по своим местам;
- отклонения и погрешность;
- как меняется форма графика в зависимости от начальных условий.
Про это будет в следующих выпусках.
Что дальше
В следующий раз смоделируем работу нормального распределения на практике: будем виртуально подбрасывать много кубиков и посмотрим, будут значения распределяться нормально или нет. А потом сделаем красивую визуализацию и посмотрим, что влияет на показатели в графике.