У нашего кумира Code Bullet есть видео, где он пишет алгоритм для победы в игре «4 в ряд».
В ролике есть одна любопытная деталь: Эван (который Code Bullet) решает задачу перебором всех возможных значений и понимает, что их число слишком велико, чтобы их можно было быстро перебрать на компьютере. В итоге он использует один хитрый трюк, чтобы сократить количество переборов и ускорить работу алгоритма.
Если вы знаете английский, то лучше посмотрите видео, а если нет — почитайте наш краткий пересказ.
Что такое «4 в ряд»
Есть два игрока, один из которых играет красными фишками, а второй — жёлтыми. Ещё есть игровое поле — 7 ячеек в ширину и 6 в высоту. Игроки по очереди роняют фишки своего цвета в любой столбец, а цель игры — собрать 4 фишки своего цвета в ряд по горизонтали, вертикали или диагонали.

Эван хочет написать алгоритм, который будет выдавать самый лучший следующий ход для любого положения фишек.
Готовим поле
Как обычно, Эван делает всё по шагам, маленькими порциями добавляя новые возможности в код. Это нужно для того, чтобы быстро проверять, в том ли направлении идёт алгоритм, и если нет — быстро его поправить.
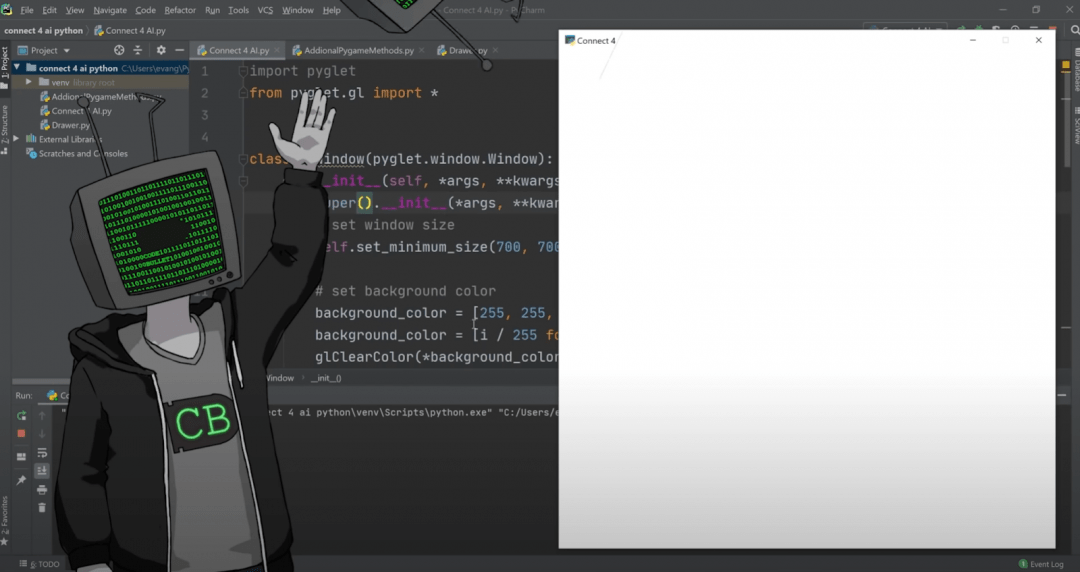
Сначала он рисует окно, в котором нет вообще ничего — просто окно будущей программы, чтобы убедиться, что код вообще работает:
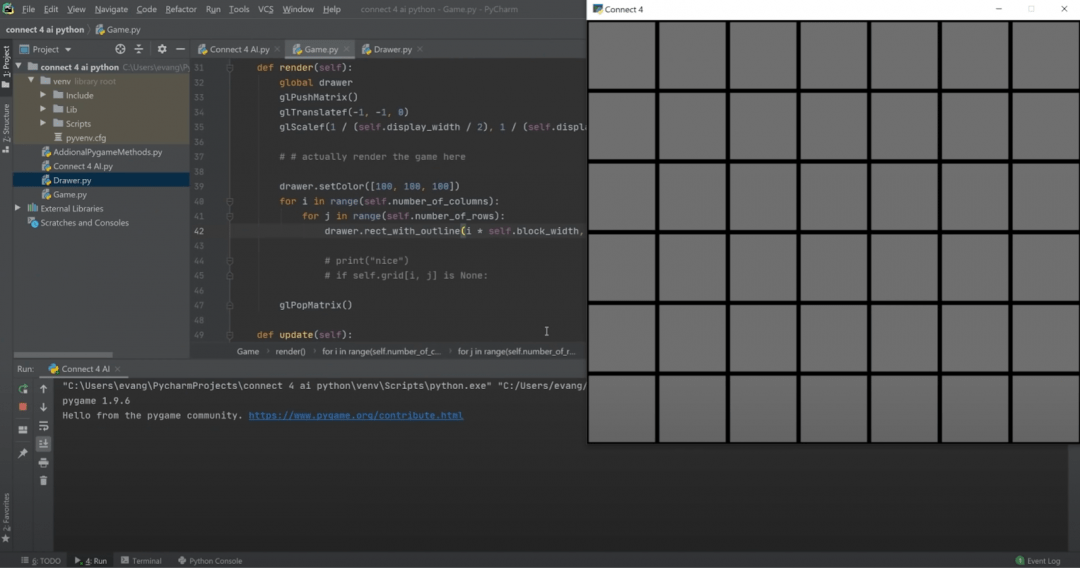
Потом Эван добавляет разбиение игрового поля на квадраты, чтобы увидеть игровую сетку:
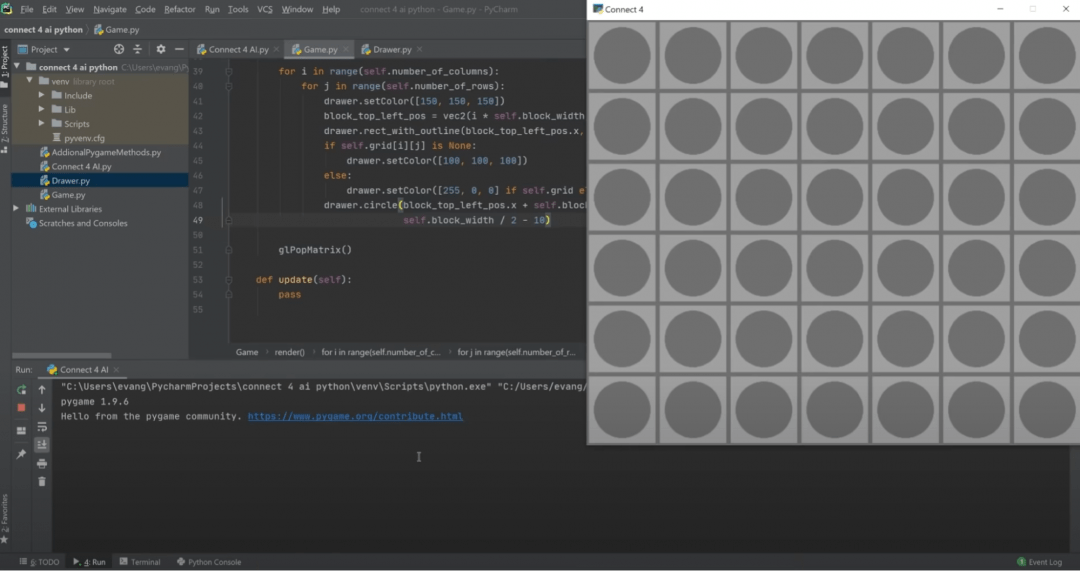
Финальный штрих: квадраты превращаются в круги, чтобы игра была похожа на настоящую:
Добавляем круги
Поле готово, можно добавлять круги, заодно проверяя, как они ложатся в поле по своим координатам:
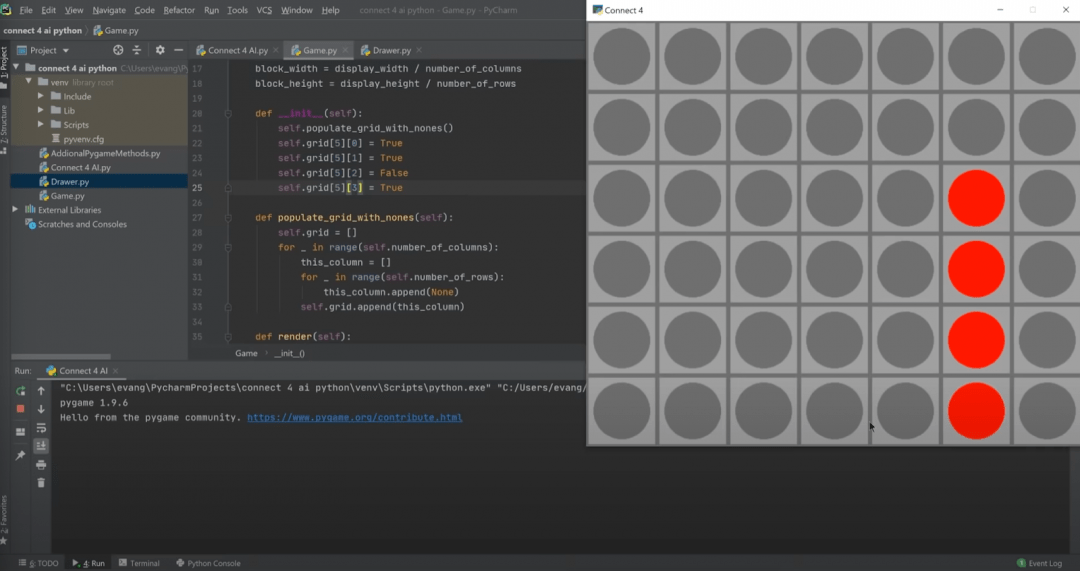
Но здесь Эвана ждёт первая неприятность: он забыл предусмотреть падение фишек вниз, как это происходит в настоящей игре. В итоге фишки висят в воздухе и ломают всю логику:
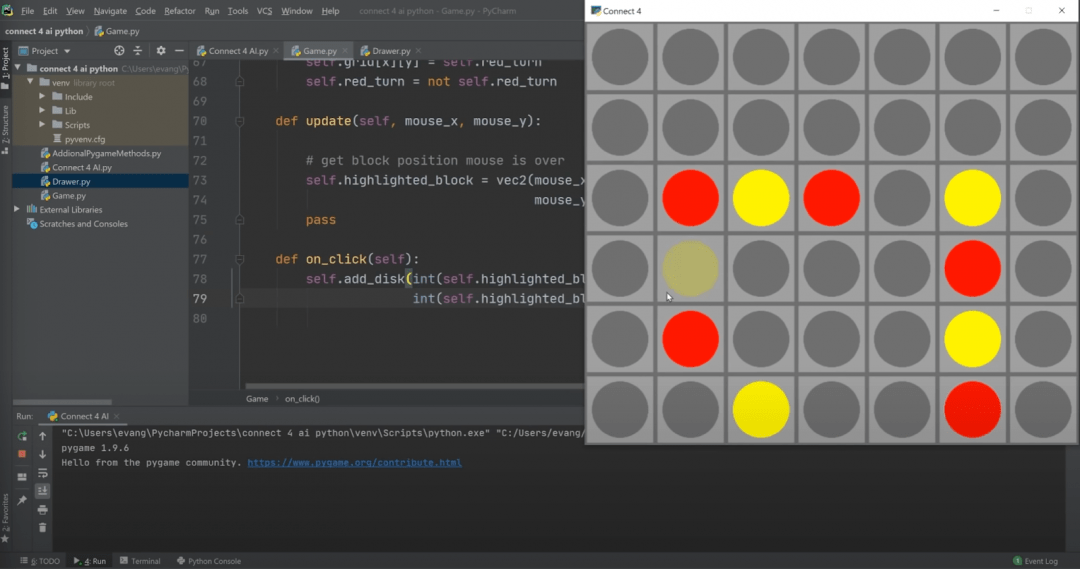
Добавляем проверку на пустые ячейки внизу, и если они есть — роняем фишку вниз до упора. Теперь всё работает как нужно:

Это уже достаточно, чтобы можно было просто играть в игру, но нам нужен алгоритм для победы, поэтому двигаемся дальше.
Определяем наилучший ход
Эван решает построить выигрышный алгоритм по такой стратегии:
- Берём текущую расстановку фишек на поле.
- Строим для неё все возможные варианты следующего хода и смотрим, есть ли среди них выигрышный. Если нет — идём дальше.
- Для каждых из этих вариантов строим все возможные варианты следующего хода и смотрим, есть ли среди них выигрышный. Если нет — идём дальше.
- Для каждых из новых вариантов строим все варианты и так далее до тех пор, пока не закончатся клетки на поле или пока не найдём выигрышную комбинацию.
После того как все варианты будут перебраны, алгоритм выбирает самый лучший из них — тот, который вероятнее всего ведёт к победе.
👉 Здесь Эван исходит из логики «жадных» алгоритмов: если принимать наилучшее решение на каждом ходу, то это автоматически приведёт к выигрышу (или как минимум позволит сделать ничью).
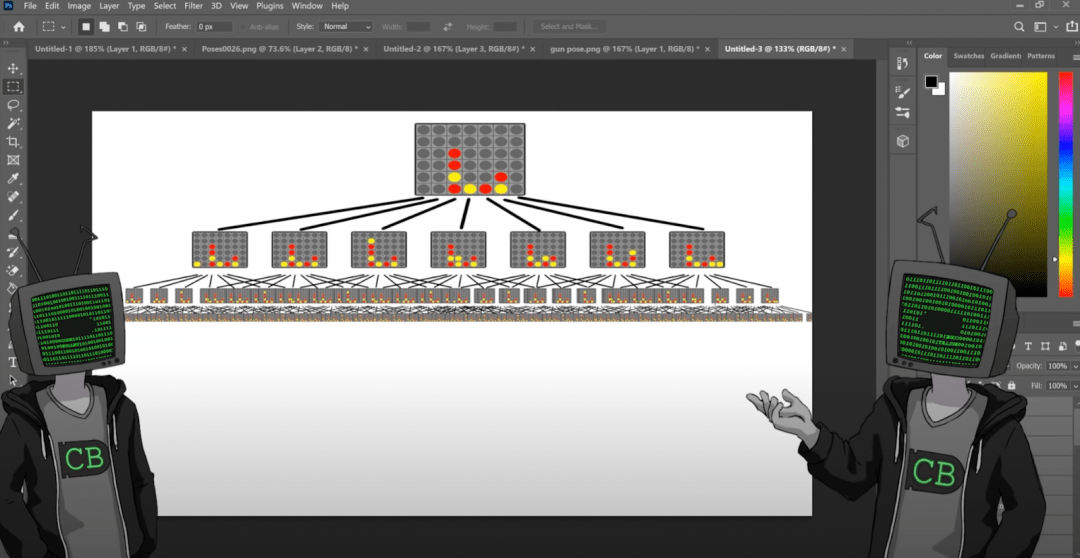
Графически это можно представить так:
Когда Эван запускает свой алгоритм, то он зависает на первом же ходу:
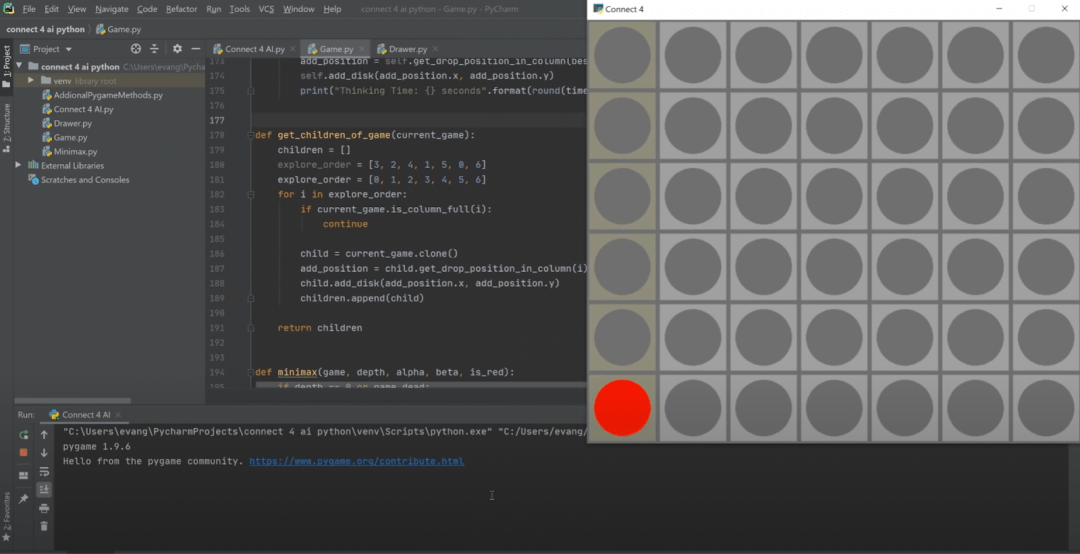
Проблема этого подхода в том, что компьютеру нужно перебрать, обработать и проверить миллиарды миллиардов комбинаций для каждого хода. В итоге компьютер зависает навечно и результата нет.
Оптимизация — таблицы проверенных ходов
Чтобы ускорить работу своего алгоритма, у Эвана есть три пути:
- Переписать код на C++, что даст ему некоторый прирост производительности и эффективности.
- Заняться оптимизацией алгоритма с математической точки зрения.
- Сжульничать и подсмотреть работающее решение, а потом внедрить его себе.
Варианты 1 и 2 — это правильно, но долго, поэтому Эван выбирает третий и идёт читать материалы Паскаля (Pascal Pons), который уже нашёл решение этой проблемы.
Первое, что делает Эван — создаёт таблицу проверенных ходов. Это значит, что компьютер на каждом ходу заглядывает в таблицу с расстановками и смотрит, есть там такая позиция или нет. Если есть, то алгоритм берёт из этой таблицы уже готовый наилучший ход для этой ситуации, а если нет — просчитывает расстановку сам и записывает в таблицу наилучший ход.
Такой подход сокращает время обработки каждого хода, потому что после разных ходов могут получиться одинаковые расстановки, у которых будет одинаковое продолжение. Нам остаётся только заглянуть в таблицу и выяснить, было такое уже или нет.
Чтобы сгенерировать себе такую таблицу, Эван идёт на хитрость: он заходит на сайт Паскаля, где можно сыграть против его алгоритма. После этого Эван перепрограммирует свой код так, чтобы он играл против алгоритма Паскаля и записывал в табличку каждый его ход:
Через два дня непрерывной работы программы Эван посчитал, сколько записей у него получилось в таблице: около 15 000 записей. Это значит, что его алгоритм может моментально обработать 15 000 расстановок, а остальные придётся считать самостоятельно. Проблема в том, что всего расстановок в этой игре в 300 000 раз больше: 4 531 985 219 вариантов. Это значит, что два дня непрерывной работы кода оптимизировали нашу игру всего на 0,0000033%. Нужен другой подход.
Оптимизация таблиц — улучшенный вариант
Чтобы сократить количество вариантов для перебора, Эван придумывает другой ход: играть против алгоритма Паскаля всего 6 ходов, потом сбрасывать и начинать всё сначала. Кажется, что выхлоп от этого будет такой же мизерный, но на самом деле нет.
Дело в том, что короткие партии по 6 ходов с каждой стороны играются намного быстрее, чем полные, а значит, можно быстрее найти все варианты расстановок после первых 6 ходов.
С другой стороны, полностью сыгранные 6 ходов с каждой стороны дадут нам примерно 1 миллион возможных расстановок (сравните с 15 000 вариантами в первом случае). Это значит, что если игра не найдёт текущую расстановку в таблице, ей достаточно будет проверить всего 4500 комбинаций, записать найденный результат в таблицу и выдать правильный ход. Такое компьютер может сделать за пару секунд.
В итоге Эван получил алгоритм, который почти сразу выдаёт наилучший ход и не проигрывает ни одной партии.
И что? Мне-то это зачем, я же не собираюсь играть в игры?
А вот зачем:
- Каждый алгоритм можно оптимизировать несколькими способами. Выбор способа зависит от времени, ресурсов и результата, который нам нужно получить.
- Нет правильного и неправильного подхода к оптимизации алгоритмов, всё зависит от внешних условий. Если бы код Эвана должен был быстро работать в карманной игрушке на дешёвой микросхеме, ему пришлось бы переписывать его на C++, потому что там лучше производительность.
- Если нет ограничений, которые могут повлиять на проект, можно выбрать любую оптимизацию, даже ту, которая кажется нечестной, но даёт нужный результат.
- Необязательно использовать нейросети, чтобы научить алгоритм играть в игры.
- Если кто-то уже написал оптимизированный алгоритм, который подходит для вашей задачи, можно его брать и использовать у себя в проекте. Почти всегда реальное программирование — это не поиск и придумывание самой оригинальной идеи, а использование того, что подходит лучше всего.