В девяностых наш математик Андрей Леонович Тоом преподавал в США математику студентам колледжей и давал им разные интересные задачи. Если что, это тот самый Тоом, в честь которого назвали новый алгоритм вычислений с низкой сложностью (осторожно, Википедия).
Так вот, задача:
Марк Твен на лодке проплыл по Миссисипи по течению за 5 дней, а против течения то же расстояние он проплыл на этой же лодке за 7 дней. За сколько дней Марк Твен проплыл бы это расстояние, если бы у реки не было течения?
 Что не так с челленджем из Тиктока на скорость сбора бутылок: разбираем как математики
Что не так с челленджем из Тиктока на скорость сбора бутылок: разбираем как математики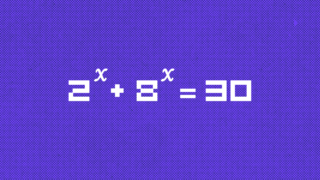 Что не так с задачей про степени, которую нужно РЕШИТЬ УСТНО, и как она всё-таки решается
Что не так с задачей про степени, которую нужно РЕШИТЬ УСТНО, и как она всё-таки решается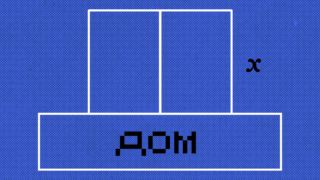 Необычная задача с Реддита про чувака и периметр забора
Необычная задача с Реддита про чувака и периметр забора Задача про золото для тех, кто нестандартно мыслит
Задача про золото для тех, кто нестандартно мыслит Интересная задача про велосипеды, которую можно решить намного быстрее, чем кажется
Интересная задача про велосипеды, которую можно решить намного быстрее, чем кажется Безумная задача про среднюю скорость, которую все решают неправильно
Безумная задача про среднюю скорость, которую все решают неправильноКажется, что всё просто, но нет. Многие студенты попались в эту ловушку простоты, но мы уверены, что вы не из таких.
Большинство студентов бодро и за минуту решили так: берём дни туда, дни оттуда и делим пополам, чтобы найти среднюю скорость с учётом разного направления течения.
В итоге получилось такое: (5 + 7) / 2 = 6 дней.
Но математика так не работает: в этом решении вообще не учитывается влияние скорости, а берётся только время. И это — неправильный подход. А правильный — ниже.
Чтобы решить эту задачу, нам нужно учесть все факторы — и расстояние, и скорость лодки, и скорость течения.
Обозначим скорость лодки за Л, а скорость течения — за Т. Дистанцию, соответственно, обозначим за Д, а расстояние от точки до точки — за Р. Теперь у нас есть всё что нужно.
Чтобы посчитать дистанцию, нужно скорость умножить на время.
Когда Марк Твен плыл по течению, его скорость была равна (Л + Т) и он проплыл всё за 5 дней. Получается, что расстояние равно:
Р = 5 × (Л + Т)
А когда он плыл 7 дней обратно, его скорость была равна (Л − Т), потому что он плыл против течения, и расстояние считается так (и помним, что это то же самое расстояние, что и в начале):
Р = 7 × (Л − Т)
Теперь умножим обе части первого равенства на 7, а второго — на 5. Так как мы обе части умножаем на одно и то же число, равенство сохраняется:
7Р = (Л + Т) × 35 → 7Р = 35Л + 35Т
5Р = (Л − Т) × 35 → 5Р = 35Л − 35Т
Сложим два получившихся равенства:
12Р = 35Л + 35 Л + 35Т − 35Т
12Р = 70Л
Получается, что скорость лодки равна: Л = 12Р / 70.
Запомним это и вернёмся к формуле расчёта времени от расстояния и скорости. Чтобы найти время, за которое пройдётся какое-то расстояние, нужно это расстояние разделить на скорость движения:
Время = Расстояние (Р) / Скорость
Расстояние мы знаем — это Р. Скорость лодки мы тоже знаем — 12Р / 70. Разделим одно на другое, чтобы получить время, за которое лодка пройдёт по реке, которая никуда не течёт (и лодка просто плывёт со своей скоростью):
Время = Р / (12Р / 70)
Время = 1 / (12/70) = 70 / 12
Выходит, что время, которое потребуется Марку Твену для того, чтобы проплыть на лодке по Миссисипи без течения, — 70 / 12 дней. Разделим и получим — 5,83 дня, или 5 дней и почти 20 часов.
На 4 часа быстрее, чем при простом (и неправильном) решении :)