Часто в разработке есть задача отсортировать данные за один проход или даже по мере их появления. Классическое решение — использовать быструю сортировку, то есть сортировку вокруг опорного элемента. Но если неверно выбрать этот опорный элемент, скорость сортировки резко возрастёт. А нам это не нужно.
Чтобы не столкнуться с этой проблемой, используют сортировку слиянием.
В чём идея сортировки слиянием
Основной принцип сортировки слиянием такой: делим массив пополам, каждый из них сортируем слиянием и потом соединяем оба массива. Каждый разделённый массив тоже нарезаем на два подмассива до тех пор, пока в каждом не окажется по одному элементу.
Здесь тоже используется рекурсия — то есть повторение алгоритма внутри самого алгоритма. Но это только один из элементов алгоритма.
Второй элемент — соединение отсортированных элементов между собой, причём тоже хитрым способом: раз оба массива уже отсортированы, то нам достаточно сравнивать элементы друг с другом по очереди и заносить в итоговый массив данные по порядку.
Если представить алгоритм по шагам, он будет выглядеть так:
- Исходный массив: [4 2 5 1].
- Делим пополам: [4 2] ←→ [5 1] (у нас появилось два новых массива, значит, к ним применяем тоже сортировку слиянием).
- Делим пополам первый массив: [4] ←→ [2].
- Раз в каждом по одному элементу, то сортируем и склеиваем в один: [2 4].
- Делим пополам второй массив: [5] ←→ [1].
- Раз в каждом по одному элементу — сортируем и склеиваем в один: [1 5].
- К нам вернулись два отсортированных подмассива, а значит, нам нужно их отсортировать и склеить в один.
- Сравниваем первые элементы: 1 и 2. Единица меньше двух, значит, в итоговый массив записываем 1, и у нас остаются два массива: [2 4] и [5].
- Сравниваем первые элементы: 2 и 5. Двойка меньше пяти, значит, в итоговый массив записываем 2, и у нас остаются два массива: [4] и [5].
- Точно так же сравниваем первые элементы до тех пор, пока в обоих массивах не исчезнут все элементы. Как только это произойдёт — массив отсортирован.
Если проще воспринимать работу алгоритма в виде картинок — держите анимацию сортировки слиянием:
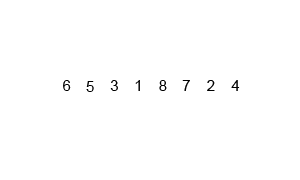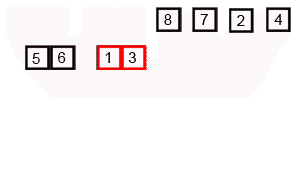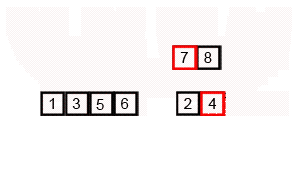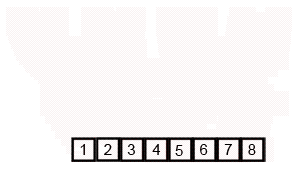
Особенность алгоритма
Главное преимущество сортировки слиянием — она работает всегда с одной и той же скоростью на любых массивах. Допустим, у нас есть два массива:
- В одном будут числа в случайном порядке.
- В другом — уже отсортированные числа, но последний и предпоследний элементы (разные) просто поменяны местами.
В обоих случаях сортировка слиянием покажет одно и то же время: ей всё равно, какие данные обрабатывать, алгоритм всё равно сделает это за один проход и одинаковое время. Благодаря этому свойству алгоритм используют там, где нужно обработать данные за заранее известное время. Например, если для сортировки 1000 элементов серверу требуется 50 миллисекунд, то можно настроить ему отправку новой партии данных каждую 51 миллисекунду — так мы будем уверены, что к моменту отправки новых данных старые уже будут обработаны.
Сортировка слиянием на JavaScript
Запустите этот код в браузере, чтобы посмотреть, на какие части алгоритм делит входной массив и как он обрабатывает их по очереди. Обратите внимание на три точки в команде return — они означают, что эта переменная может быть, а может и не быть в итоговом результате. Про то, как работают эти три точки и зачем они нужны, расскажем в отдельной статье, а пока читайте комментарии и проверяйте код в деле:
// слияние массивов с одновременной сортировкой
// на вход подаются уже отсортированные левая и правая части
function merge(left, right) {
// сюда будем складывать результат
let arr = []
// пока в каждой части есть хотя бы один элемент — выполняем цикл
while (left.length && right.length) {
// смотрим на наименьший элемент из тех, что стоят в начале обоих массивов
if (left[0] < right[0]) {
// если слева был элемент меньше —
// забираем его оттуда и отправляем в массив с результатом
arr.push(left.shift())
} else {
// в противном случае забираем элемент из правой части
arr.push(right.shift())
}
}
// выводим результат слияния отсортированных массивов
console.log('Результат: ' + arr);
// возвращаем отсортированный массив и добавляем к нему в конец отсортированный остаток от какой-либо части, если её так и не обработали в цикле
return [ ...arr, ...left, ...right ]
}
// делим массивы пополам до тех пор, пока в них не останется элементов
function mergeSort(array) {
// находим середину
const half = array.length / 2
// если в нашем массиве и так меньше двух элементов — возвращаем его
if(array.length < 2){
return array
}
// делим массив на две части и левую отправляем в новый массив
const left = array.splice(0, half)
// выводим промежуточный результат
console.log('Слева:' + left);
console.log('Справа:' + array);
// запускаем рекурсию и отдаём ей правую и левую части массива
return merge(mergeSort(left),mergeSort(array))
}
// исходный массив
array = [3, 5, 1, 6, 9, 8, 2];
console.log(mergeSort(array));