Это статья о реализации одного из алгоритмов сортировки. Эти алгоритмы считаются классикой информатики: разработчиков могут спросить об этих алгоритмах на собеседовании, а сами алгоритмы помогают ощутить силу автоматики и алгоритмов. Сегодня пощупаем один из таких алгоритмов.
Ранее в статьях мы рассказали про два вида сортировки:
- пузырьковая сортировка — самая простая, но медленная;
- сортировка расчёской — чуть сложнее, но немного быстрее.
Эти сортировки относятся к простым видам алгоритмов — надёжным, но неоптимальным по скорости и затратам памяти. Гораздо чаще вместо них используют быструю сортировку или алгоритмы на её основе — про это и будем сегодня говорить.
В чём идея быстрой сортировки
Когда в 1960 году Тони Хоар придумывал этот алгоритм, ему нужно было отсортировать данные на магнитной ленте за один проход, чтобы не перематывать плёнку много раз. Для этого он взял за основу классическую пузырьковую сортировку и преобразовал её так:
- На очередном шаге выбирается опорный элемент — им может быть любой элемент массива.
- Все остальные элементы массива сравниваются с опорным и те, которые меньше него, ставятся слева от него, а которые больше или равны — справа.
- Для двух получившихся блоков массива (меньше опорного, и больше либо равны опорному) производится точно такая же операция — выделяется опорный элемент и всё идёт точно так же, пока в блоке не останется один элемент.
Вот как это выглядит, если представить массив в виде графика:
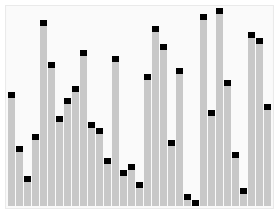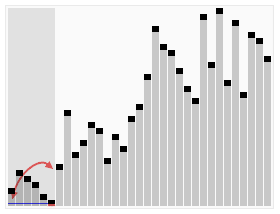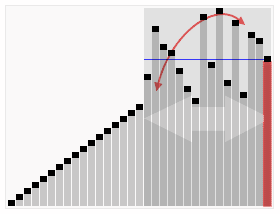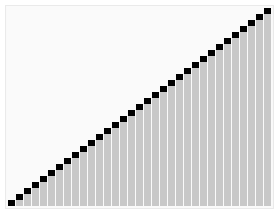
Особенности алгоритма
Так как на третьем шаге мы разбиваем массив на два и для каждой части делаем то же самое, и так снова и снова, то это значит, что в нём используется рекурсия. Рекурсия — это когда функция вызывает саму себя, и при этом ей нужно держать в памяти все предыдущие этапы. Это значит, что при использовании сразу двух рекурсий (для левой и правой частей массива), может потребоваться очень много памяти. Чтобы обойти это ограничение, используют улучшенные версии быстрой сортировки — про них поговорим в другой раз.
Но несмотря на такой возможный расход памяти, у быстрой сортировки есть много плюсов:
- это один из самых быстрых алгоритмов, когда мы заранее ничего не знаем про массивы, с которыми придётся работать;
- алгоритм настолько прост, что его легко написать на любом языке программирования;
- быструю сортировку легко распараллелить и разбить на отдельные процессы;
- алгоритм работает на данных с последовательным доступом, когда мы не можем в любой момент вернуться в начало, а должны работать с данными только в одном порядке.
Выбор опорного элемента
Правильный выбор опорного элемента может сильно повысить эффективность быстрой сортировки. В зависимости от реализации алгоритма есть разные способы выбора:
- Первый элемент — в первых версиях быстрой сортировки Хоар выбирал опорным первый элемент массива. Именно так он смог обрабатывать всю магнитную ленту за один проход.
- Средний элемент — тот, который физически стоит посередине массива.
- Медианный элемент — элемент, значение которого находится посередине между всеми значениями в массиве
Есть ещё много других техник выбора — они применяются, когда программист точно знает, с какими массивами придётся работать: немного упорядоченными или когда всё вразнобой.
Быстрая сортировка на JavaScript
Запустите этот код в консоли браузера, чтобы посмотреть, как алгоритм шаг за шагом приводит массив в нормальный вид:
// исходный массив
var arr = [3,14,1,7,9,8,11,6,4,2]
// рекурсивная функция быстрой сортировки
// на вход получает массив, который нужно отсортировать
function quickSort(arr) {
// если длина массива меньше двух (в нём один элемент или нет их вообще)
// то возвращаем массив как есть, без обработки
if (arr.length < 2) return arr;
// берём первый элемент массива как опорный
let pivot = arr[0];
// будущие левые и правые части массива
const left = [];
const right = [];
// перебираем весь массив по порядку
for (let i = 1; i < arr.length; i++) {
// если опорный элемент больше текущего
if (pivot > arr[i]) {
// то добавляем текущий элемент в левую часть
left.push(arr[i]);
// в противном случае
} else {
// добавляем текущий элемент в правую часть
right.push(arr[i]);
}
// выводим текущее состояние массива в консоль
// это необязательный шаг, он здесь для наглядности
console.log(arr);
}
// отправляем на рекурсивную обработку левую и правую части массива
// и возвращаем результат в виде двух склеенных массивов
return quickSort(left).concat(pivot, quickSort(right));
}
// запускаем сортировку
quickSort(arr);Что дальше
На этом мы закончим с обменными сортировками — впереди нас ждут интересные сортировки выбором, слиянием и даже сортировки без сравнений. Подпишитесь, чтобы не пропустить ни одной из них.