Мы как-то писали о методе Монте-Карло: он изучает случайные процессы, которые происходят в разных системах, и на основании результатов делает различные выводы. Например, с помощью метода Монте-Карло навигатор моментально находит кратчайший путь между городами, пусть и с небольшой погрешностью.
Одно из применений этого метода, когда он только появился, было нахождение числа пи. Но есть и другие способы, которые также позволяют находить число пи и при этом могут использоваться в самых разных областях жизни. Один из таких способов — задача Бюффона о бросании иглы.
В чём идея
В 18 веке французский математик Карл Бюффон открыт новый метод вычисления числа пи. В основе метода — бросание иглы случайным образом на ткань. Общую идею можно рассказать так:
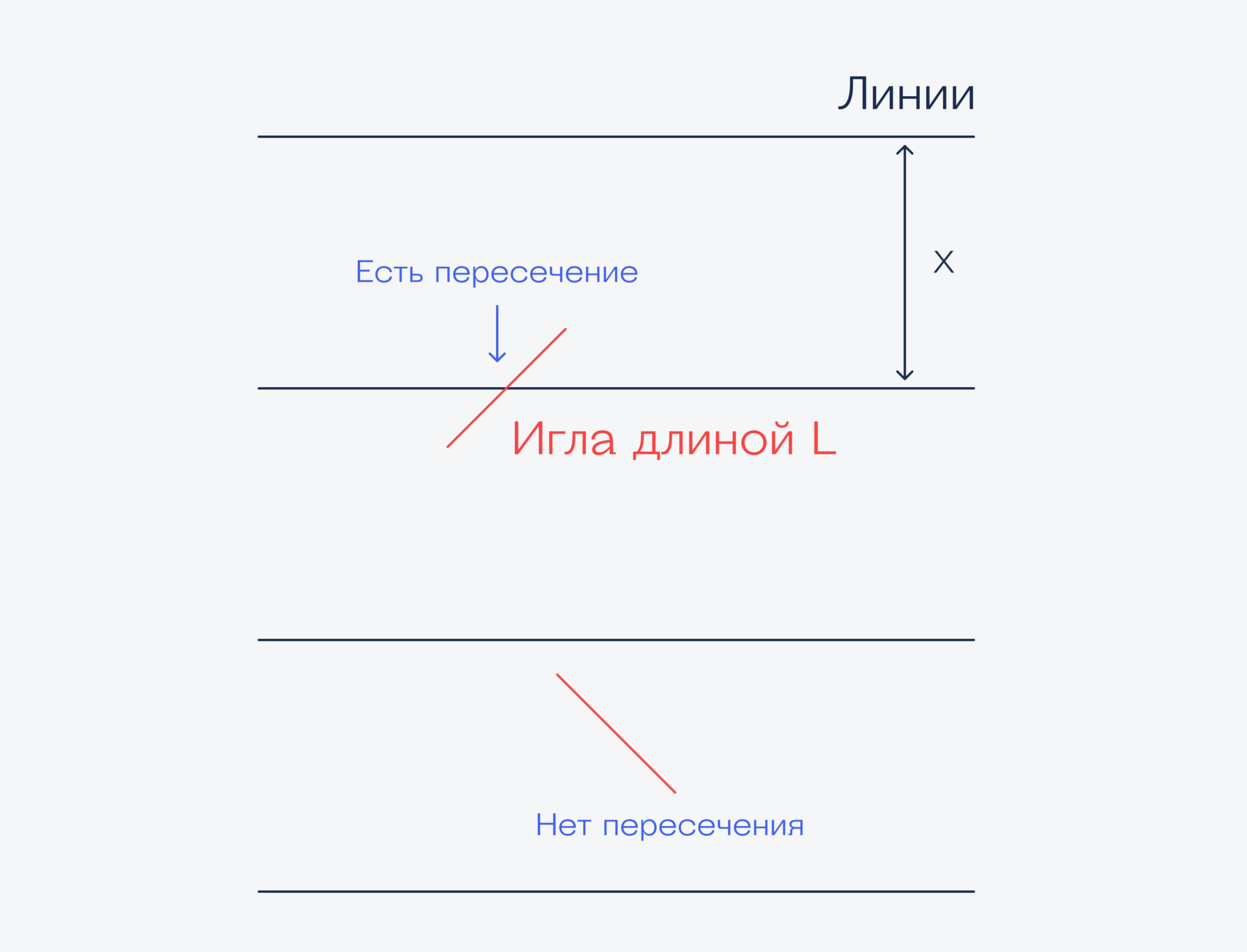
- Берём ткань и рисуем на ней параллельные линии на расстоянии X друг от друга.
- Берём иглу длиной L, но так, чтобы её длина была меньше или равна расстоянию между линиями, то есть L <= X.
- Случайным образом бросаем иглу на ткань и смотрим, попала ли игла на одну из линий или нет.
- Считаем, сколько раз мы бросили иглу и сколько раз она попала на одну из линий.
- Отношение этих двух чисел даст нам число, похожее на пи. Чем больше бросков — тем результат будет ближе к пи.
Бюффон доказал, что вероятность того, что игла попадёт на одну из линий, равна 2L/Xπ. Чтобы улучшить результат, нужно взять иглу с длиной X = L/2, то есть в два раза короче расстояния между линиями. Если так сделать, то вероятность броска иглы на линию становится равна 1/π.
Как это повторить дома
Самый простой способ повторить эксперимент Бюффона выглядит так:
- Возьмите коробок спичек и измерьте длину одной спички — пусть это будет L.
- На листе бумаги нарисуйте параллельные линии с расстоянием 2L между собой.
- Высыпьте спички из коробка и распределите их равномерно на листе.
- Забирайте спички по одной с листа, откладывая в отдельную кучку те, что попали на линию.
- Посчитайте, сколько получилось спичек в отдельной кучке и сколько их было всего.
- Разделите большее число на меньшее — вы получите число, близкое к π (3,1415926…).
- Можно взять лист А3 или А2 и несколько коробков — так результат будет точнее.

У нас две гипотезы.
Одна гипотеза — мы находимся в матрице, но на слабом сервере, и нам недоступны алгоритмы подлинных случайных чисел. Чтобы оптимизировать вычисления, программисты оптимизировали алгоритм случайности с помощью числа пи. Вот мы и видим этот алгоритм в работе.
Другая гипотеза — число пи связано с тем, как устроены естественные природные процессы, в том числе любой хаос. (Так же, как нормальное распределение.) Можно представить так: мы используем десятичную систему счисления, потому что у нас 10 пальцев на руках. А у природы и хаоса нет 10 пальцев, у них свои встроенные величины. И если привести природные величины к нашим десятичным, получится число пи.
Вот вам аналогия. В США и Великобритании для измерения расстояния используют мили, а не километры. Миля получилась от римского «тысяча шагов». Шаг — это буквально шаг римского солдата длиной примерно полтора метра. То есть буквально есть ступня римского солдата длиной 29,6 см (в России это размер 44,5). Пять таких ступней подряд — это шаг. Тысяча шагов — это миля.
А в Европе мы всё измеряем не милями, а километрами. Километр — это 1000 метров. Почему 1000? Просто так договорились. А что такое метр? Это одна десятимиллионная расстояния от Северного полюса до экватора. А километр, получается, это одна десятитысячная этого расстояния.
Как связан размер шага римского легионера и расстояние от полюса до экватора? А вот так: одна миля — это примерно 1,6 километра; а один фут — это примерно 0,3 метра. Почему такое соотношение? По кочану. Просто есть разные системы измерения, основанные на разных физических величинах.
Код, который имитирует разбрасывание спичек
Если дома нет спичек и бумаги, вот код, который можно запустить у себя на компьютере и проверить теорию на практике. Логика кода точно такая: случайным образом выбираем координаты спичек и смотрим, пересекают они линию или нет.
Для работы кода нужен Python, если не знаете, как его установить, вот статья в помощь:
# подключаем библиотеку для обработки данных
import numpy as np
# устанавливаем параметры случайного значения
np.random.seed(4)
# расстояние между линиями и высота иглы
width = 1.0
needle = 0.5
# количество пересечений и промахов
num_hits = 0
num_misses = 0
# наибольшие и наименьшие возможные координаты концов иглы
x_lo = 0.0; x_hi = 3.0
y_lo = 0.0; y_hi = 4.0
print("Начинаем симуляцию")
# запускаем цикл
for i in range(10000):
# выбираем начальные координаты иглы
x = (x_hi - x_lo) * np.random.random() + x_lo
y = (y_hi - y_lo) * np.random.random() + y_lo
# выбираем угол поворота
angle = np.radians(360.0 * np.random.random())
# конечные координаты иглы
xx = x + needle * np.cos(angle)
yy = y + needle * np.sin(angle)
# меняем координаты местами, если игла развернулась
if xx < x:
(x, xx) = (xx, x)
(y, yy) = (yy, y)
# смотрим, есть ли пересечение, и если да — увеличиваем счётчик пересечений
if (x < 0.0 and xx > 0.0) or (x < 1.0 and xx > 1.0) or (x < 2.0 and xx > 2.0) or (x < 3.0 and xx > 3.0):
num_hits += 1
# увеличиваем счётчик промахов на единицу
else:
num_misses += 1
# считаем соотношение попаданий и бросков
pr = (num_hits * 1.0) / (num_hits + num_misses)
# считаем число пи
pi_est = (2.0 * needle) / (pr * width)
# выводим результаты
print("Длина иглы: %0.1f " % needle)
print("Расстояние между линиями: %0.1f " % width)
print("Количество пересечений: " + str(num_hits))
print("Количество промахов: " + str(num_misses))
print("Рассчитанное значение числа Пи: %0.4f" % pi_est)Зачем это было нужно
Так раньше учёные и математики изучали связь между случайными событиями и известными им числами — есть связь или нет. С помощью таких исследований они пытались найти закономерности в разных областях жизни и смотрели, можно ли это как-то применить в обычной жизни.
Компьютеров тогда не было, поэтому часто единственный способ проверить теорию на практике — это подбрасывать много раз иглы и смотреть, пересекают они линии или нет.
Где это применяется сейчас
В наше время значение числа пи можно узнать с точностью до любого знака после запятой — уже есть алгоритмы, которые позволяют это сделать. Но алгоритм Бюффона применяется сейчас не для этого, а чтобы определить вероятности и параметры для разных случайных процессов.
Представим, что мы хотим провести серию экспериментов в космосе в условиях невесомости. Для этого нам нужно, чтобы во время эксперимента не работали корректировочные двигатели — те, которые стабилизируют космический аппарат на его орбите. Если мы будем знать длительность одного эксперимента (длину иглы) и общее количество экспериментов, которые нам нужно провести, то можем рассчитать вероятность включения двигателей во время эксперимента (расстояние между линиями) и количество испорченных серий. Это значит, что мы сможем скорректировать ход эксперимента и построить его так, чтобы получить нужный нам объём результатов с учётом испорченных.
Что дальше
В следующий раз сделаем не просто код в консоли, а нарисуем красивую визуализацию с разбросанными спичками на странице. Подпишитесь, чтобы не пропустить новый проект.