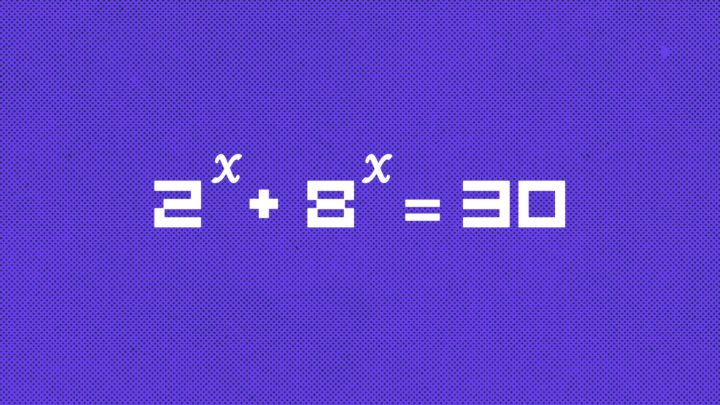Вот одна из задач на ютубе — нужно решить устно уравнение:
Ключевое слово — устно. Давайте сначала посмотрим, как это сделал автор ролика, а потом поговорим про действительно устное решение.
Итак, что делает автор в решении:
- Выносит двойку в степень во втором слагаемом.
- Подставляет другую переменную вместо двойки в степени икс.
- Получает кубическое уравнение.
- Делит в столбик его на один из корней, вычтенных из подставленной переменной.
- Получает новое кубическое уравнение.
- Раскладывает его на произведение квадратного уравнения и скобки (мы всё ещё делаем это устно, да).
- Считаем дискриминант и находим корни квадратного уравнения.
- Подставляем значения в заменённую переменную и получаем итоговый ответ.
Всё это сопровождается решением на виртуальной доске:
И предполагается, что мы всё это делаем УСТНО. Возможно, кто-то считает, что такие вычисления в уме делать очень легко, а те, кто этого не может, просто отсталые имбецилы, которые не учились в школе, но то не так. Это сложные вычисления, и абсолютно нормально не уметь считать это в голове без ручки и бумаги.
Как это часто бывает, комментарии к ролику оказались содержательнее статьи (у нас такое тоже бывает, тут всё в порядке, не переживайте :) Воспользуемся коллективным знанием и выведем действительно устное решение задачи.
Первое, что мы сделаем — докажем (устно, конечно же), что решение у задачи только одно. Следите за руками:
- Функция возведения в степень Х непрерывно возрастает при увеличении этого икса. Про это говорят в школе, но так как это не самое часто используемое знание, про него часто забывают, поэтому просто напомнили.
- По этому же правилу сумма двух возрастающих функций тоже непрерывно возрастает. Проще говоря, чем больше икс, тем больше значение функции в этой точке.
- Раз функция непрерывно возрастает, а у нас она в какой-то момент становится равна 30 (то есть одно значение), то и решение тоже будет только одно.
Кажется, что с этим вполне можно справиться действительно устно. Идём дальше.
Обозначим двойку в степени икс за t и сделаем вот такую замену:
Если что, 8 = 2³, а когда степень в степени, их можно менять местами. Это сделать в уме уже немного сложнее, но можно — мы просто заменили мысленно одно на другое.
Теперь, после этой замены, у нас получилось такое:
t + t³ = 30
Выглядит страшновато, поэтому упростим себе задачу: попробуем простым перебором целых чисел решить это уравнение. Это тоже можно сделать в уме, потому что там надо сложить два числа (ну и умножить пару раз одно само на себя). Что получается при таком подходе:
1 + 1³ = 2 ← не подходит
2 + 2³ = 2 + 8 = 10 ← не подходит
3 + 3³ = 3 + 27 = 30 ← о, сработало!
Мы только что в уме решили перебором это уравнение и выяснили, что t = 3. Теперь вернёмся к тому, что t — это двойка в степени икс:
Получается, что самое сложное здесь — перейти от степени к логарифму. Это неочевидный ход, потому что после школы про логарифмы многие забывают. Но если помните — наш почёт и уважение.
Если что, сам логарифм считать необязательно — в математике такой ответ тоже считается правильным.