Начинаем рассказывать, как работают привычные технологии: компьютерный звук, видео, MP3, вещание и стриминги, всевозможные алгоритмы и всё подобное.
👍 У этой статьи нет никакой практической ценности, она просто для удовольствия. Иногда можно себя побаловать :-)
Немного школьной физики
Звук — это колебания воздуха. Как волны на воде, только в воздухе. Воздух давит нам на уши, а в ушах есть чувствительные части, которые тонко чувствуют колебания воздуха. Эти колебания люди воспринимают как звук. В открытом космосе звуков нет, потому что там нет воздуха. И людей.
Частота. Чем быстрее колебания, тем тоньше воспринимаемый нами звук. Человек воспринимает колебания от 20 раз в секунду до примерно 20 тысяч раз в секунду. По-другому это называется частотой колебаний: герцами. То есть диапазон, который мы слышим — от 20 герц до 20 килогерц.
Для сравнения, собаки слышат от 40 герц до 60 килогерц, поэтому собачий свисток не воспринимается людьми, но очень хорошо слышен собакам. Собачий свисток как раз звучит в диапазоне 23–54 КГц.
Амплитуда. Чем сильнее колебания — тем громче, и наоборот. Можно представить, что это высота волн на поверхности пруда: может быть мелкая рябь (тихий звук), а могут быть большие мощные волны.
График. Если мы произнесём фразу «Привет, это журнал „Код“», то с точки зрения волн он будет выглядеть как-то так (очень примерно):
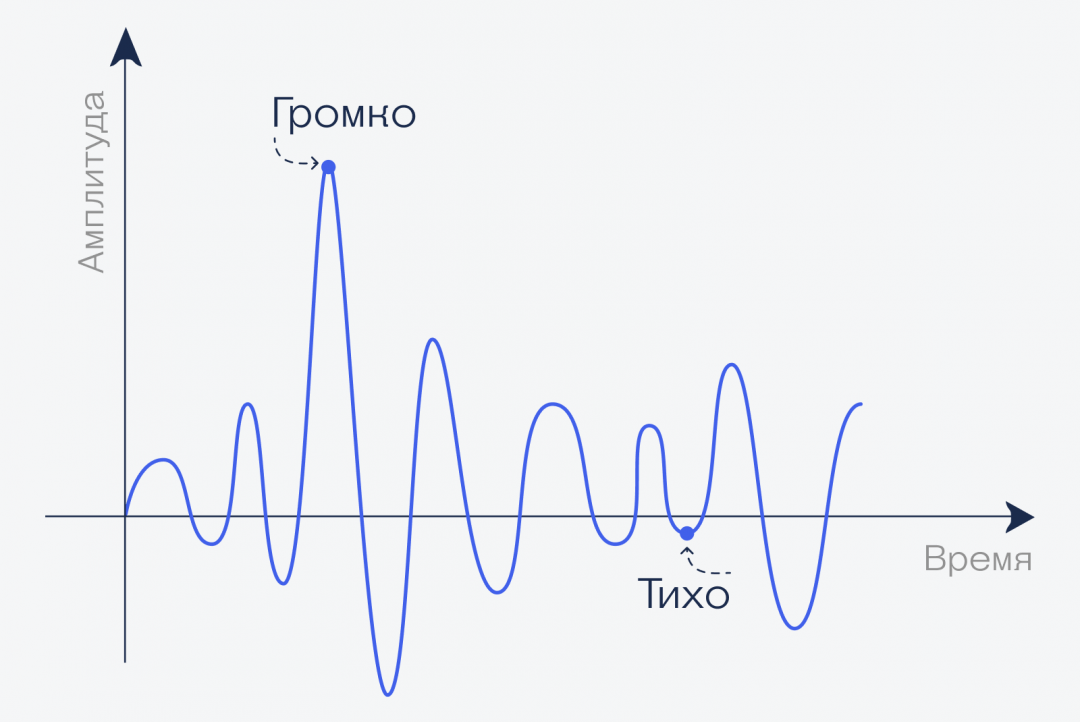
Делим звук на отрезки
Давайте увеличим наш график и посмотрим, что происходит, например, за одну секунду (опять же, очень примерно и упрощённо!):
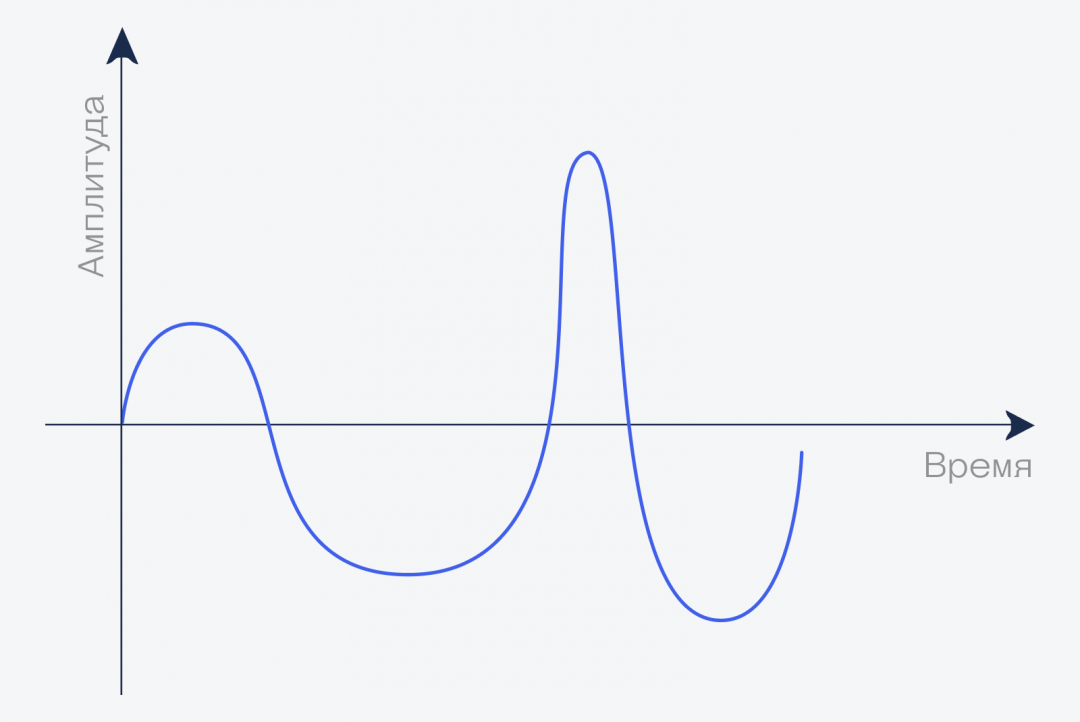
А теперь сделаем вот что: разделим секунду на 4 части, и для каждой найдём значение амплитуды:
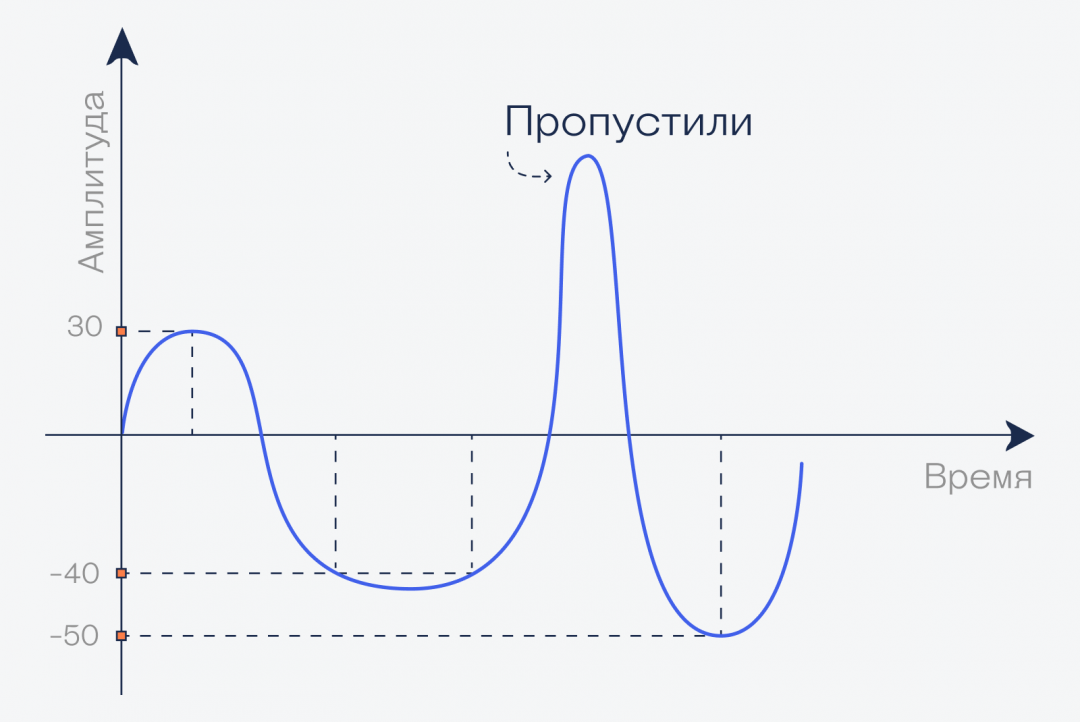
Мы измерили значение амплитуды в каждой из четырёх точек, получили, условно говоря, четыре числа: +30, −50, −50 и −60. Теоретически, если взять ток и подать эти четыре напряжения на динамик, у нас получится воспроизвести тот же звук. Но есть несколько проблем:
- Из-за того, что мы замерили волну только в четырёх местах, мы пропустили целое колебание. Оно было настолько быстрым, что уместилось между нашими ключевыми точками.
- Опять же, из-за больших отрезков мы получим очень грубый звук по сравнению с оригиналом. Это то же самое, как взять картину с тысячей разных оттенков и нарисовать её тремя цветами, не смешивая их.
Дискретизация с частотой 4 (сколько значений мы измеряем в секунду) — это слишком мало для звука. Чтобы получить более или менее разборчивую речь, нужно секунду делить на 8 тысяч отрезков, а для музыки обычно хватает 41 тысячи.
Увеличим частоту дискретизации: нарежем звук на более мелкие кусочки за ту же единицу времени:
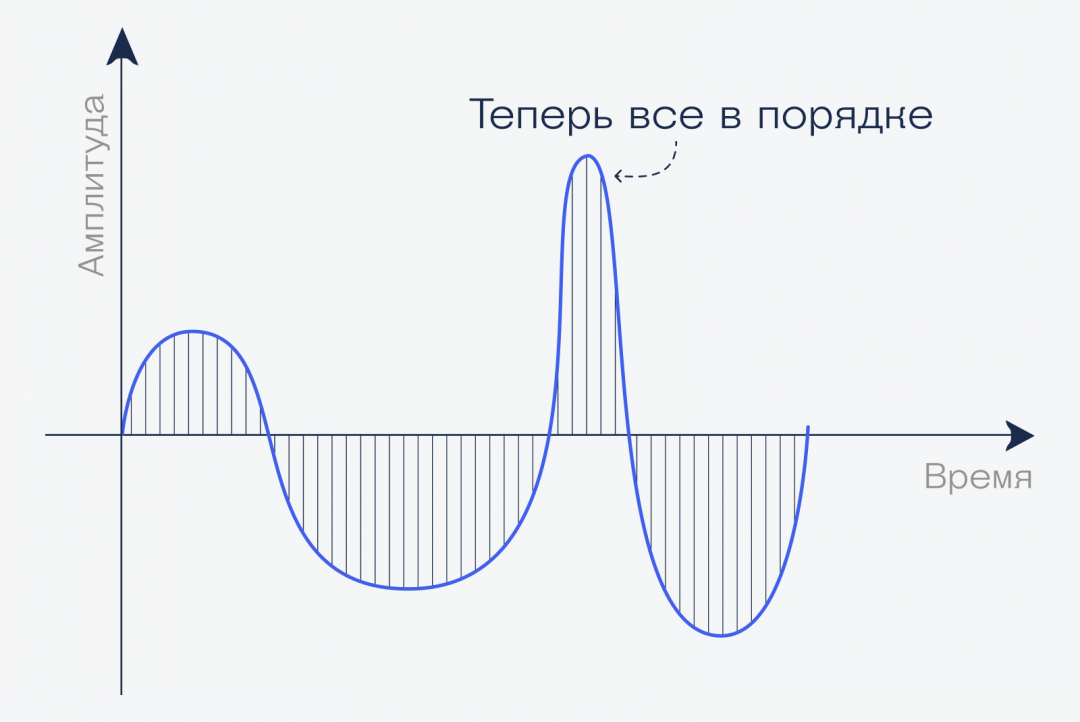
Переводим в цифру
После того как мы разбили звук на мелкие отрезки и измерили значение амплитуды для каждого из них, мы можем записать это в виде таблички:
| Время | Амплитуда |
| 0.01 сек. | 5 |
| 0.02 сек. | 7 |
| 0,03 сек | 10 |
| ... | ... |
| 1 сек | −21 |
Если мы весь звук разбиваем на одинаковые отрезки, то время можно не писать, потому что мы знаем, как оно меняется, достаточно записать в строчку только значения амплитуды:
5 7 10 … −21
Чтобы компьютер понимал эти числа, переведём эти числа в двоичную систему счисления. Для простоты будем считать, что одно число занимает ровно один байт памяти, но на самом деле чем больше байт выделяется на число, тем точнее будет измерение и качество звука. После перевода получим такое:
00000101
00000111
00001010
…
11101011
Последнее большое число получилось оттого, что нам нужно хранить и отрицательные значения, поэтому первая единица в байте означает, что это отрицательное число и его нужно считать немного иначе.
Вот эту последовательность компьютер уже может понять и воспроизвести в виде звука.
Как теперь воспроизвести звук
Чтобы что-то зазвучало, нужно сделать следующие шаги:
- Взять колонки или наушники — что угодно, что умеет «толкать воздух», то есть создавать акустические волны. В колонках за это отвечают динамики, к которым подключены специальные мягкие конусы, которые, собственно, и создают колебания воздуха. Та круглая ерунда в колонке — это и есть конус.
- Подать на эти колонки некий ток. От того, насколько мощный этот ток, конус будет двигаться по-разному.
- Чтобы получить этот меняющийся ток, нужен специальный чип под названием ЦАП — цифро-аналоговый преобразователь. Он получает на вход число, а на выходе дает ток. У всех ваших смартфонов и компьютеров есть такие ЦАПы.
Итого:
- Процессор отправляет цифры из звукового файла в ЦАП.
- ЦАП получает числа и выдаёт меняющееся электричество по этим цифрам.
- Электричество попадает в колонку, передаётся на динамик.
- Динамик из-за электричества начинает двигать конус колонки.
- Конус начинает толкать воздух перед собой, создавая звуковые волны.
- Волны долетают до наших ушей, и мы воспринимаем их как звук.
Что дальше
У такого способа есть одна проблема: файл получается слишком большим, чтобы им было удобно пользоваться. Представьте: 44 тысячи чисел за одну секунду!
Чтобы уменьшить размер файла, придумали два решения: сжатие с потерями и без них. Каждое разберём отдельно, несмотря на то, что у них много общего.













