А вот вам четверговая логическая и математическая задачка.
В одной ИТ-компании офис разбили так, чтобы у 15 программистов и менеджера было по своему кабинету. Для этого офис разделили на 16 помещений и сделали сквозные двери в каждом кабинете. Менеджер сидит в первом офисе, а общий вход и выход — через кабинет №16:
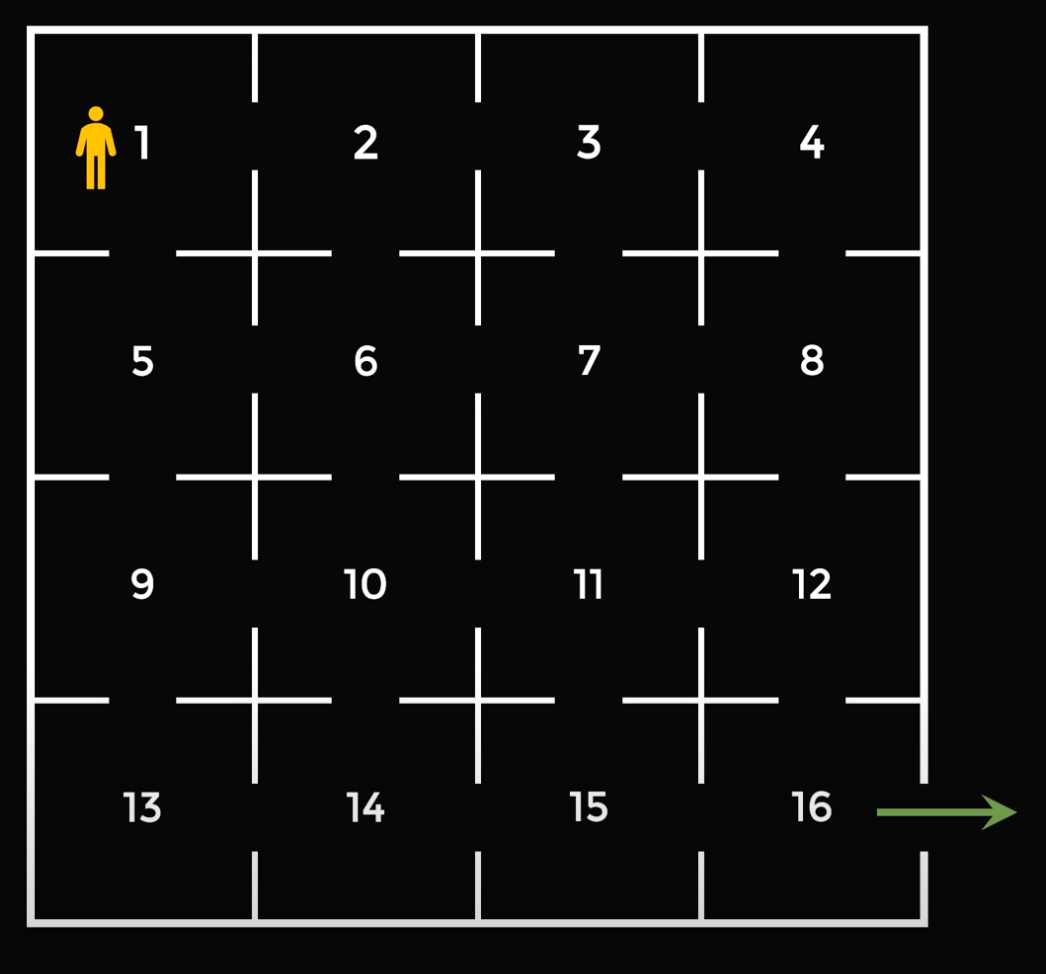
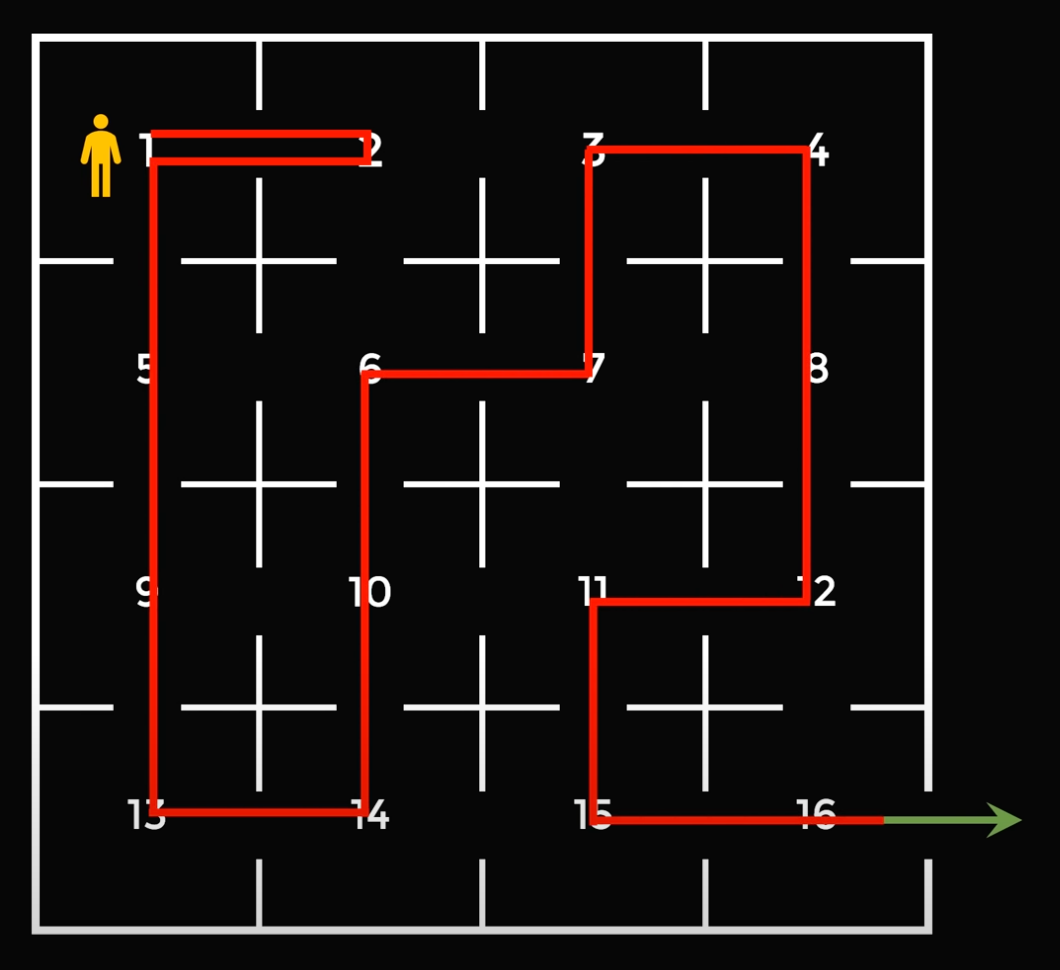
В конце рабочего дня менеджер решает обойти всех программистов, чтобы узнать, что они сделали за день. Он не хочет встречаться с одним и тем же программистом дважды и хочет построить маршрут так, чтобы встретиться с каждым по одному разу и финальным шагом выйти через общую дверь. Какой маршрут ему нужно построить?
Математическая теория говорит про это так: невозможно в такой конфигурации обойти каждый кабинет только один раз, чтобы выйти из кабинета №16. Чтобы это доказать наглядно, раскрасим кабинеты как шахматную доску:
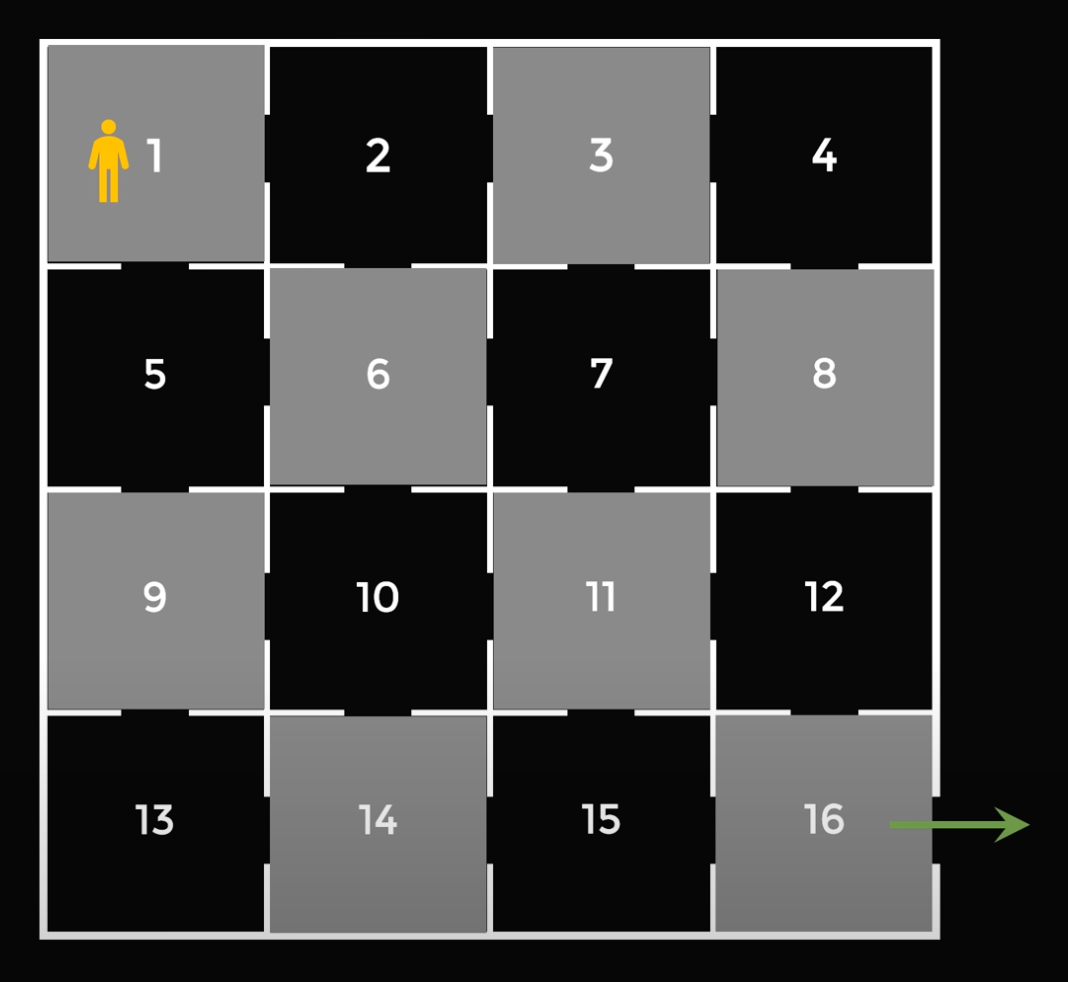
Каждый шаг между кабинетами — это перемещение с белой клетки на чёрную и наоборот. Нам нужно пройти 15 кабинетов, а значит — сделать 15 ходов. Если количество ходов нечётное, то старт и финиш будут на клетках разного цвета:
- один ход: с белой на чёрную;
- два хода: белая → чёрная → белая;
- три хода: белая → чёрная → белая → чёрная и так далее.
Но у нас клетки 1 и 16 одного цвета, а значит, дойти до финиша без повторений и возвратов не получится. Такая теория, кстати, работает для всех шахматных досок с размерностью N×N, где N — чётное число.
Получается, что у этой задачи нет решения даже в теории и менеджеру придётся заглянуть к кому-то дважды.
Хитрость в том, что в задаче нас просят не обойти каждый кабинет один раз, а встретиться с каждым программистом один раз :-) Это сразу меняет дело, следите за руками:
1. Менеджер переходит в кабинет 2 и встречается там с программистом.
2. После этого он возвращается в свой кабинет, который пустой — там никого нет, поэтому менеджер там никого не встретит. Это ключевой момент решения: пустой кабинет позволяет нам увеличить количество шагов на единицу, чтобы обойти ограничение теории из предыдущего раздела. Таким способом мы делаем 16 шагов, и это значит, что первая и последняя клетка должна быть одного цвета, как нам и нужно.
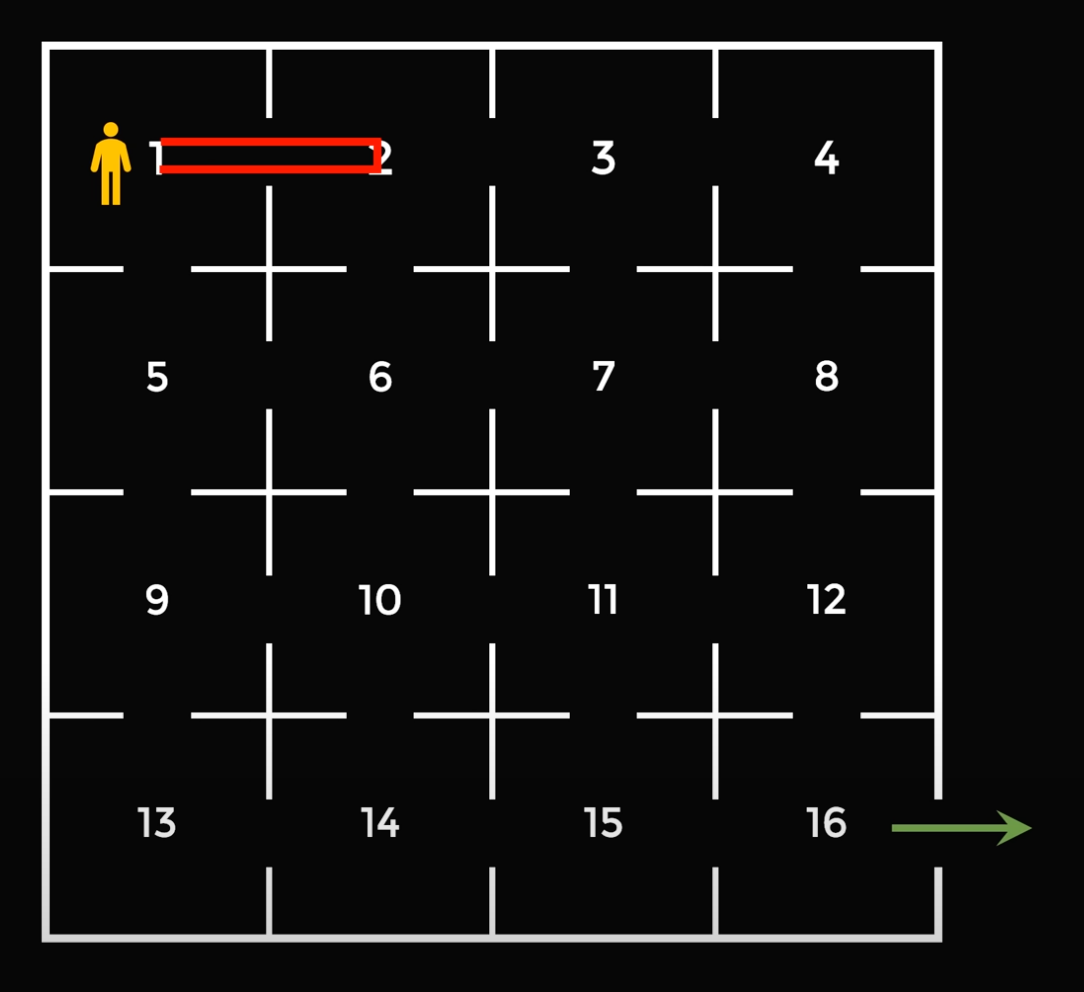
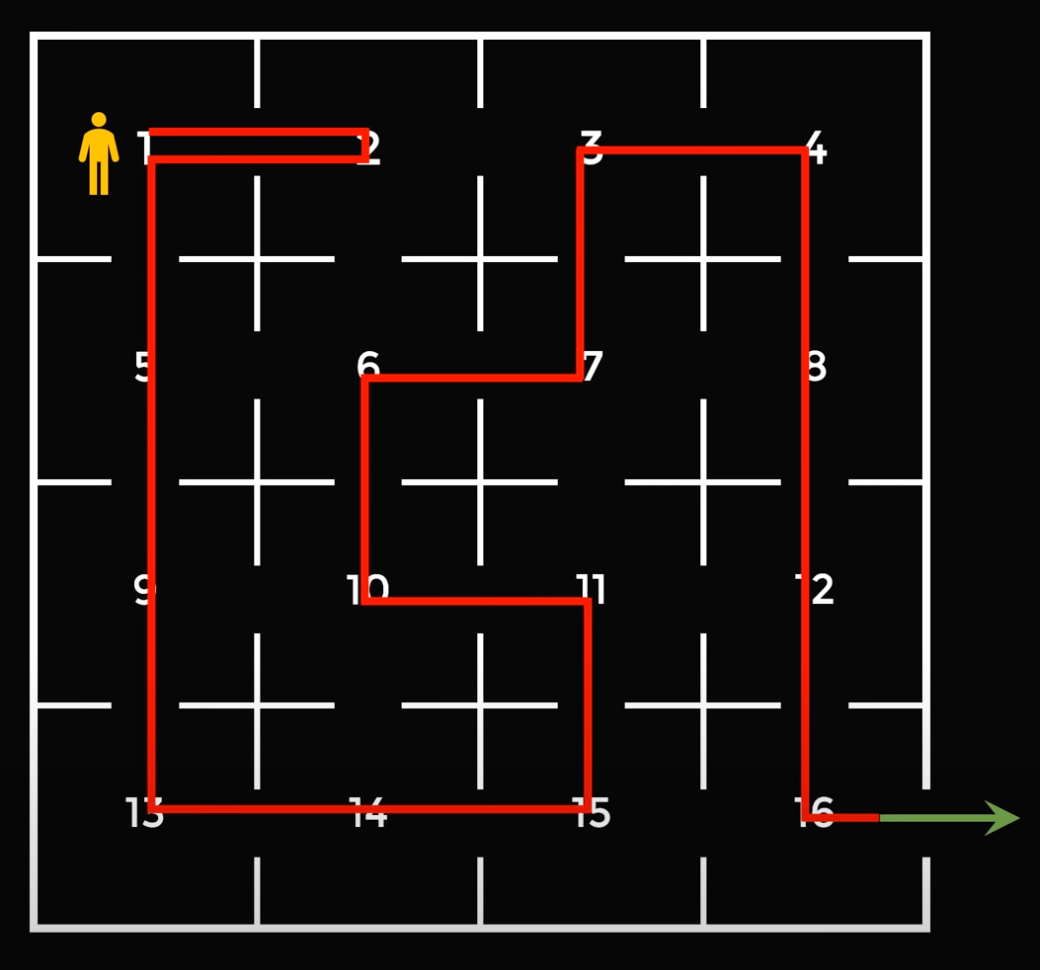
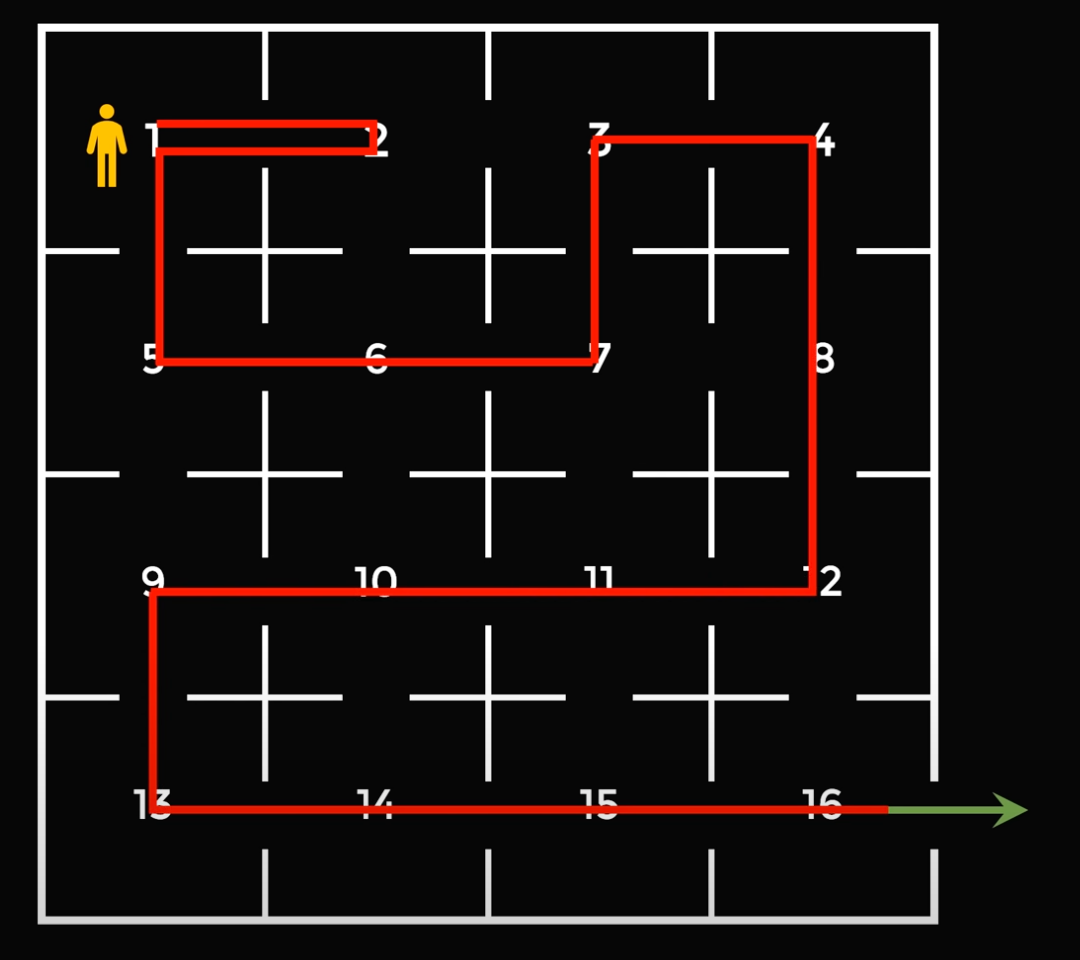
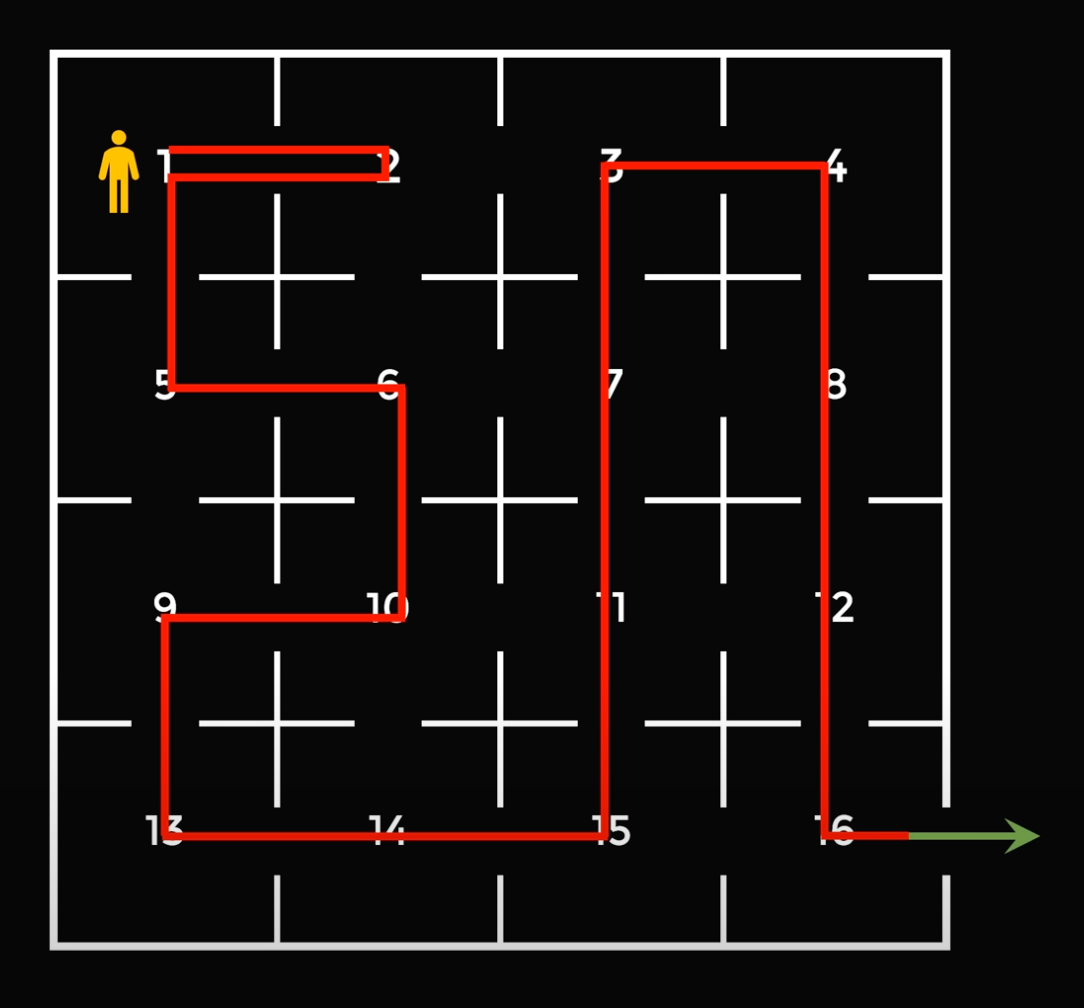
3. После этого менеджер обходит остальные 14 кабинетов и заходит в каждый по одному разу. Всего таких маршрутов будет 4: