В забеге участвовало три лошади. На финише первая лошадь опередила вторую на 11 метров и третью — на 90 метров. А когда финишировала вторая, она опередила третью на 80 метров. А теперь внезапный вопрос:
❓ сколько метров от старта до финиша?
Чтобы было проще рассуждать и искать решение, нарисуем пару картинок.
Вот на сколько метров первая лошадь опередила вторую:
А вот та же ситуация на финише первой относительно третьей лошади. Сразу посчитаем расстояние между второй и третьей в момент финиша первой лошади:
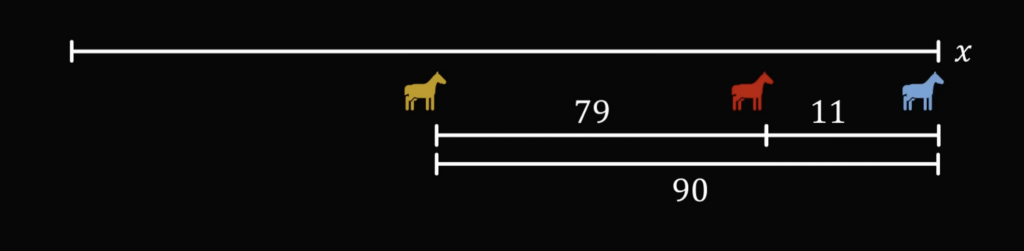
Теперь посмотрим на финиш второй лошади и расстояние в этот момент до третьей:
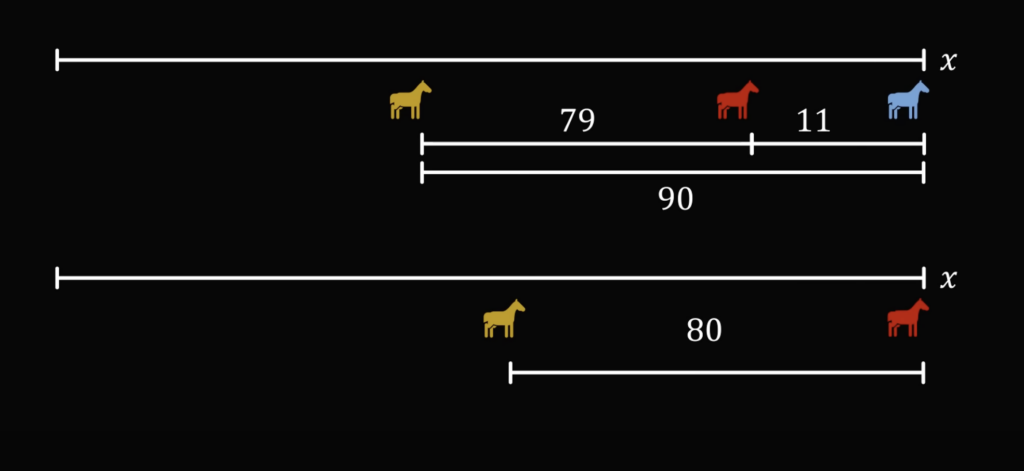
Дальше начинается самое интересное. Первая лошадь уже финишировала и для расчётов она нам сейчас не сильно нужна. Но нам важна скорость лошадей — второй и третьей. После того как первая лошадь финишировала, второй оставалось до финиша 11 метров. А когда и вторая финишировала, третья лошадь за это время пробежала 10 метров.
Ещё раз: вторая лошадь за то же время пробежала 11 метров, а третья — 10 метров:
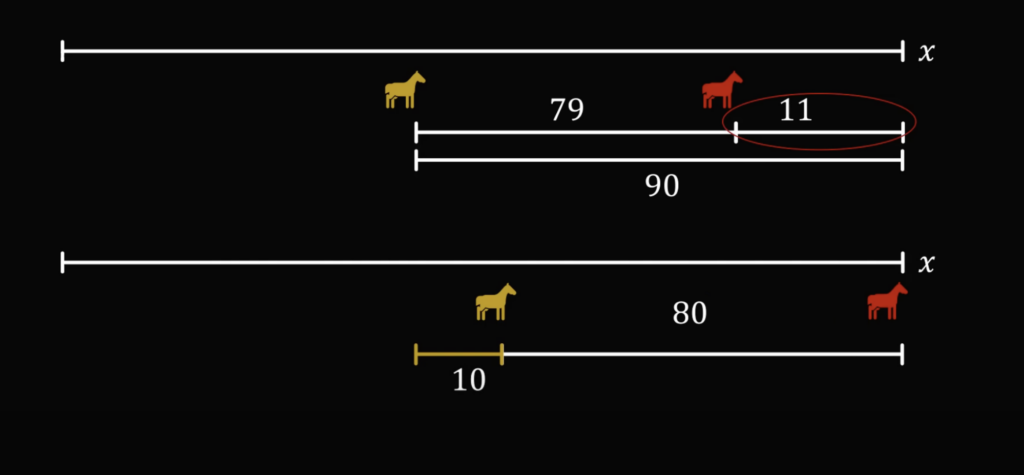
Это значит, что мы можем найти соотношение скоростей второй и третьей лошади — так как время одинаковое, то это соотношение будет зависеть только от пройденного расстояния:
Скорость 3-й лошади / Скорость 2-й лошади = 10/11
Теперь, зная это, попробуем посчитать общее расстояние трассы от старта до финиша — и сразу обозначим его за x, а время, которое нужно второй лошади, чтобы пробежать всю трассу, — за t. Можно посчитать, что в таком случае общее расстояние равно:
x = t × Скорость 2-й лошади
Но так как третья лошадь бежит медленнее, за то же время t она пробежит чуть меньшее расстояние — x − 80:
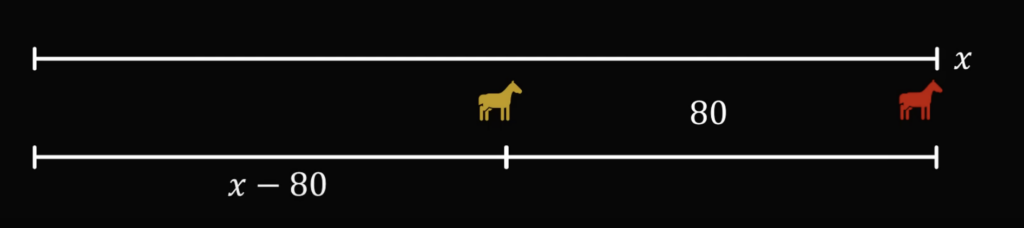
Зная это, составим второе уравнение:
x − 80 = t × Скорость 3-й лошади
Разделим первое уравнение на второе:
(x − 80) / x = (t × Скорость 3-й лошади) / (t × Скорость 2-й лошади)
В правой части у нас есть одинаковый множитель в числителе и знаменателе — t. Сократим его:
(x − 80) / x = (Скорость 3-й лошади) / (Скорость 2-й лошади)
Но мы в самом начале уже выяснили соотношение скоростей 3-й и 2-й лошади — оно равно 10/11. Заменим правую часть на это значение:
(x − 80) / x = 10/11
Решим это простое уравнение:
11(x − 80) = 10x
11x − 880 = 10x
11x − 10x = 880
x = 880
Вот мы и нашли общую длину трассы — 880 метров! Хотя на первый взгляд казалось, что это будет очень сложно, но мы справились.
Вам слово
Приходите к нам в соцсети поделиться своим мнением о задаче и почитать, что пишут другие. А ещё там выходит дополнительный контент, которого нет на сайте — шпаргалки, опросы и разная дурка. В общем, вот тележка, вот ВК — велком!
