Эту задачу дают старшеклассникам, но многие из них не могут с ней справиться без подсказки (или вообще не могут). Уверены, что вы — сможете, поэтому вот задача:
Внутренний угол в градусах между часовой и минутной стрелками, когда на часах двадцать минут восьмого?
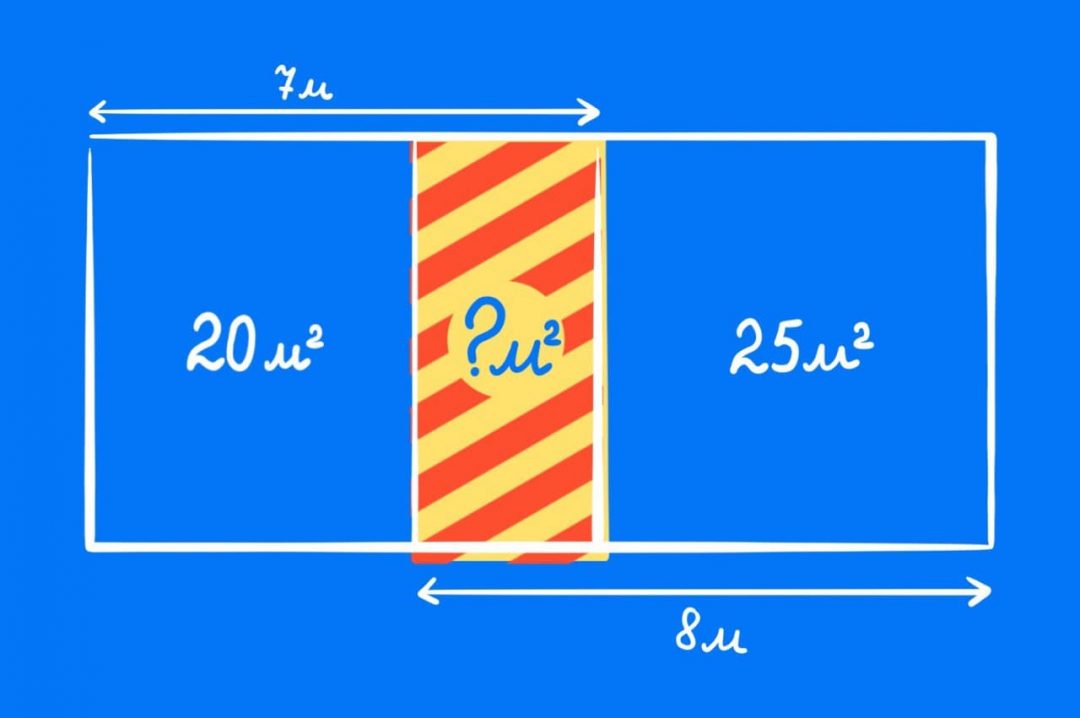
 Задача про кубик, которую очень сложно решить в уме, но очень просто — на бумаге
Задача про кубик, которую очень сложно решить в уме, но очень просто — на бумаге Несложная задача на логику про три коробки и приз
Несложная задача на логику про три коробки и приз Самая неочевидная задача по математике, которую вы встречали
Самая неочевидная задача по математике, которую вы встречали Головоломная задача про соревнования на лошадях
Головоломная задача про соревнования на лошадях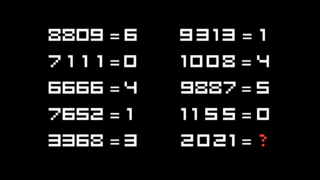 Задача на смекалку, которую невозможно решить обычными способами
Задача на смекалку, которую невозможно решить обычными способами Задача, где почти все врут, но нужно выяснить правду
Задача, где почти все врут, но нужно выяснить правдуМы сейчас не будем городить огород с формулами, а используем знания геометрии из средней школы.
Чтобы было проще решить эту задачу, нарисуем время на часах:
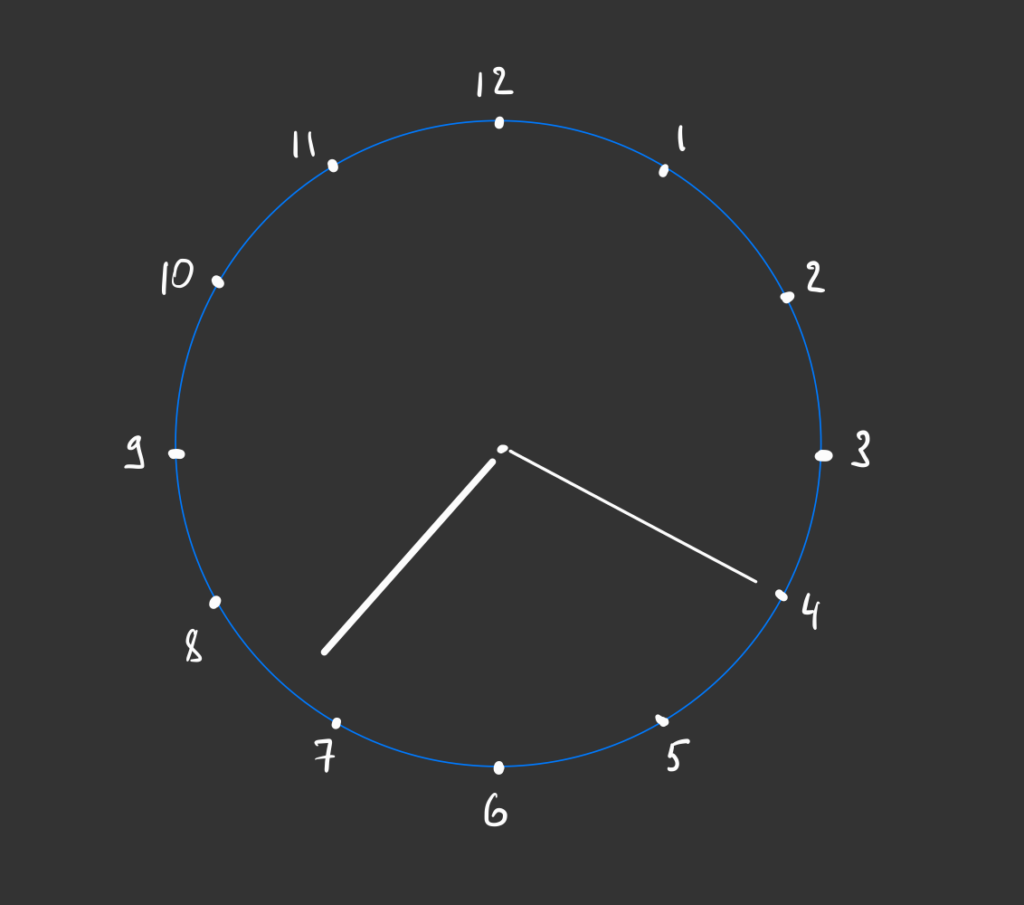
Теперь разделим циферблат на 4 части — линиями от 12 до 6 и от 9 до 3:
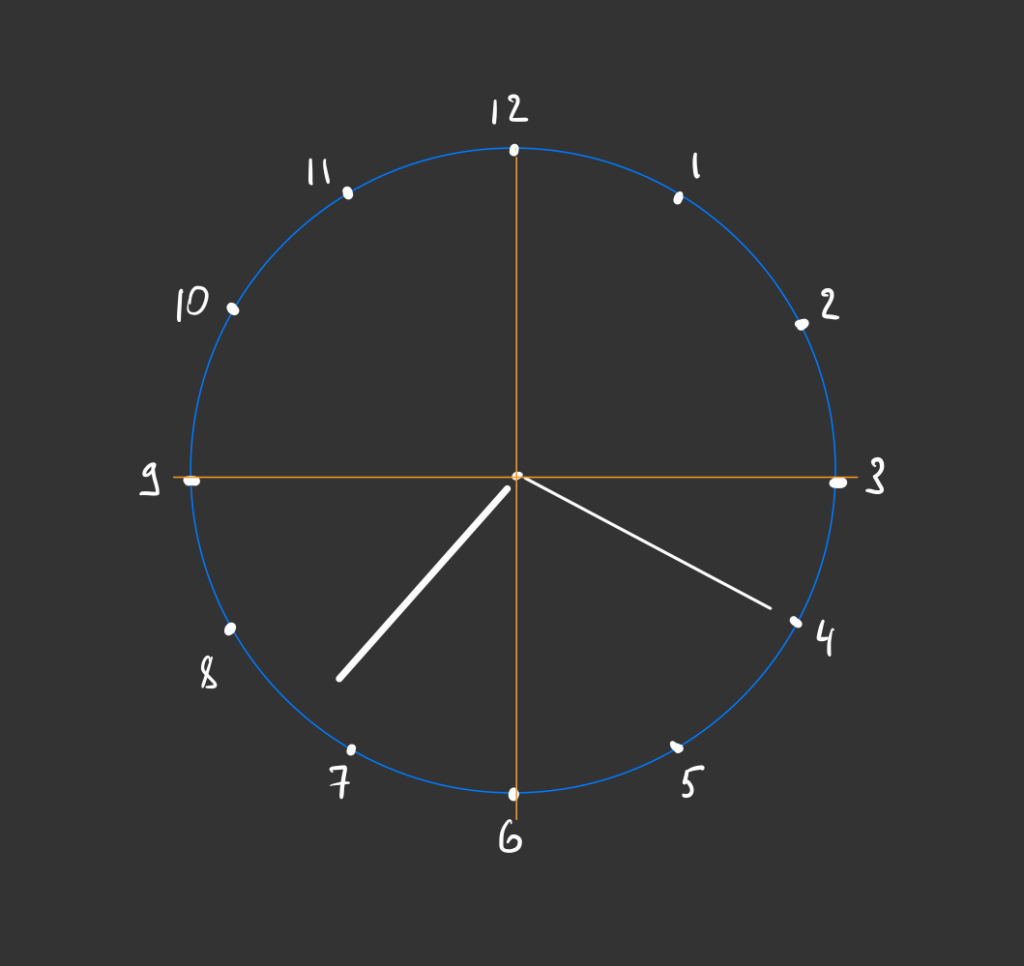
А теперь посчитаем пару углов по отдельности, чтобы потом их сложить и получить результат. Начнём с этого:
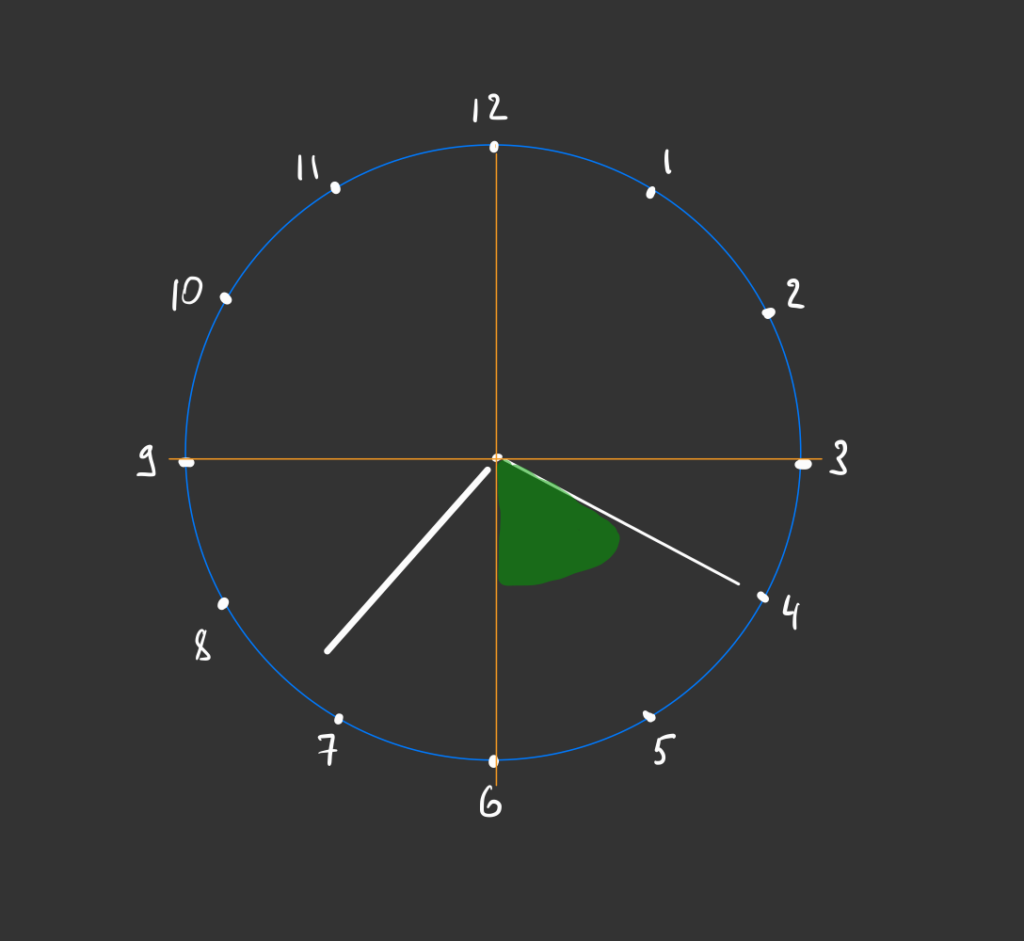
Один сектор (который, например, с 3 до 6 часов) — это 90 градусов. Получается, если минутная стрелка прошла треть этого сектора, то она делит сектор на 30 и 60 градусов соответственно (потому что треть от 90 — это 30):
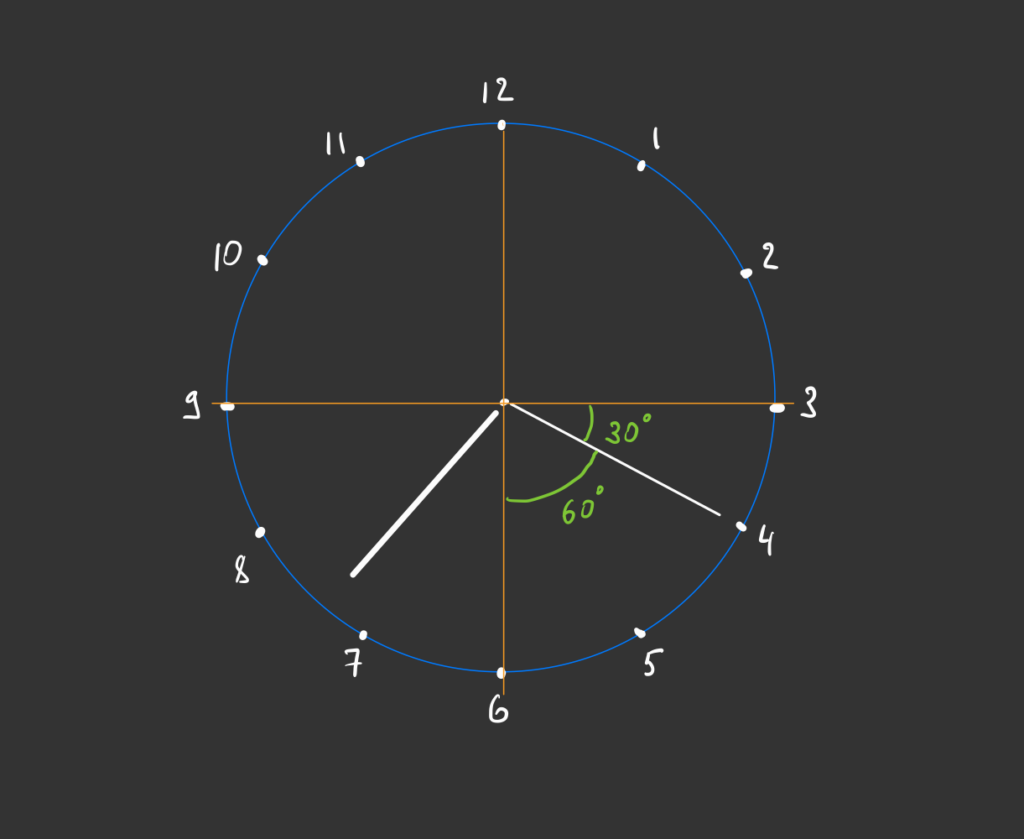
Теперь посмотрим на сектор 9—6. Если бы часовая стрелка была на 7, то она бы отклонилась от оси 12—6 тоже на 30 градусов. Но у нас двадцать минут восьмого, поэтому стрелка отодвинулась от семёрки и нам нужно понять, на сколько градусов.
Так как минутная стрелка сейчас показывает 20 минут, это значит, что прошла треть часа. Между 7 и 8 часами — 30 градусов (за такое определение геометры нас распнут, но суть ясна). За 20 минут часовая стрелка, соответственно, тоже отодвинулась от семёрки на треть углового расстояния — то есть на треть от 30 градусов.
Треть от 30 градусов — это 10 градусов. Получается, что часовая стрелка отклонилась от оси 12—6 на 30 + 10 = 40 градусов:
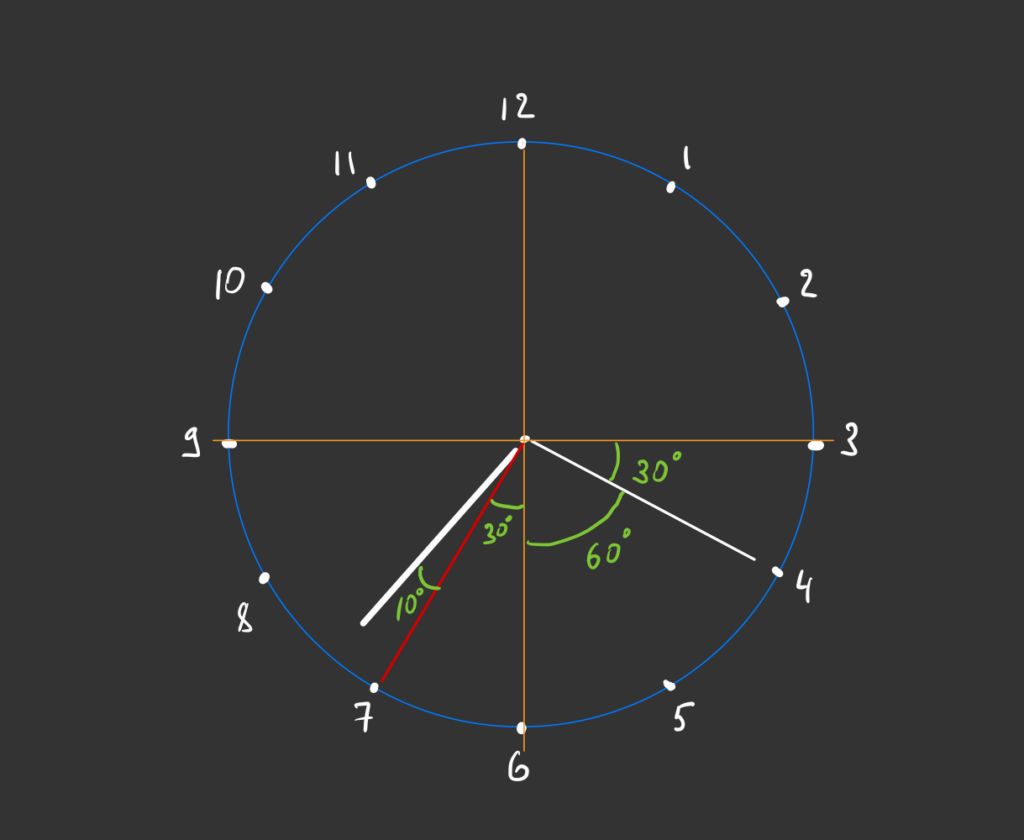
Нам остаётся только сложить оба угла, чтобы получить итоговое значение угла:
60 + 40 = 100 градусов
Но у этой задачи есть ещё и второй способ, как можно её решить, — с простыми формулами и чистой математикой. Если найдёте — поделитесь им в комментариях, чтобы другие тоже знали.