Эти задачи — одновременно простые и сложные.
Они простые по своей сути и иногда по решению. Но это не значит, что их все точно будет просто решить.
И они сложные — в той части, где нужно сначала додуматься до простого (или даже очевидного) решения. И мы любим такие задачи именно за этот кайф: поработать мозгом, чтобы тебя осенило и ты такой «Ааааа, точно, здесь же всё просто!».
В общем, развлекайтесь и тренируйте мозг. Для разминки держите задачу про шаблонное мышление.
Про шаблонное мышление
Условия этой задачи предельно просты: попробуйте по первым пяти фигурам понять, по какому шаблону строится рисунок и что должно быть на шестой картинке?
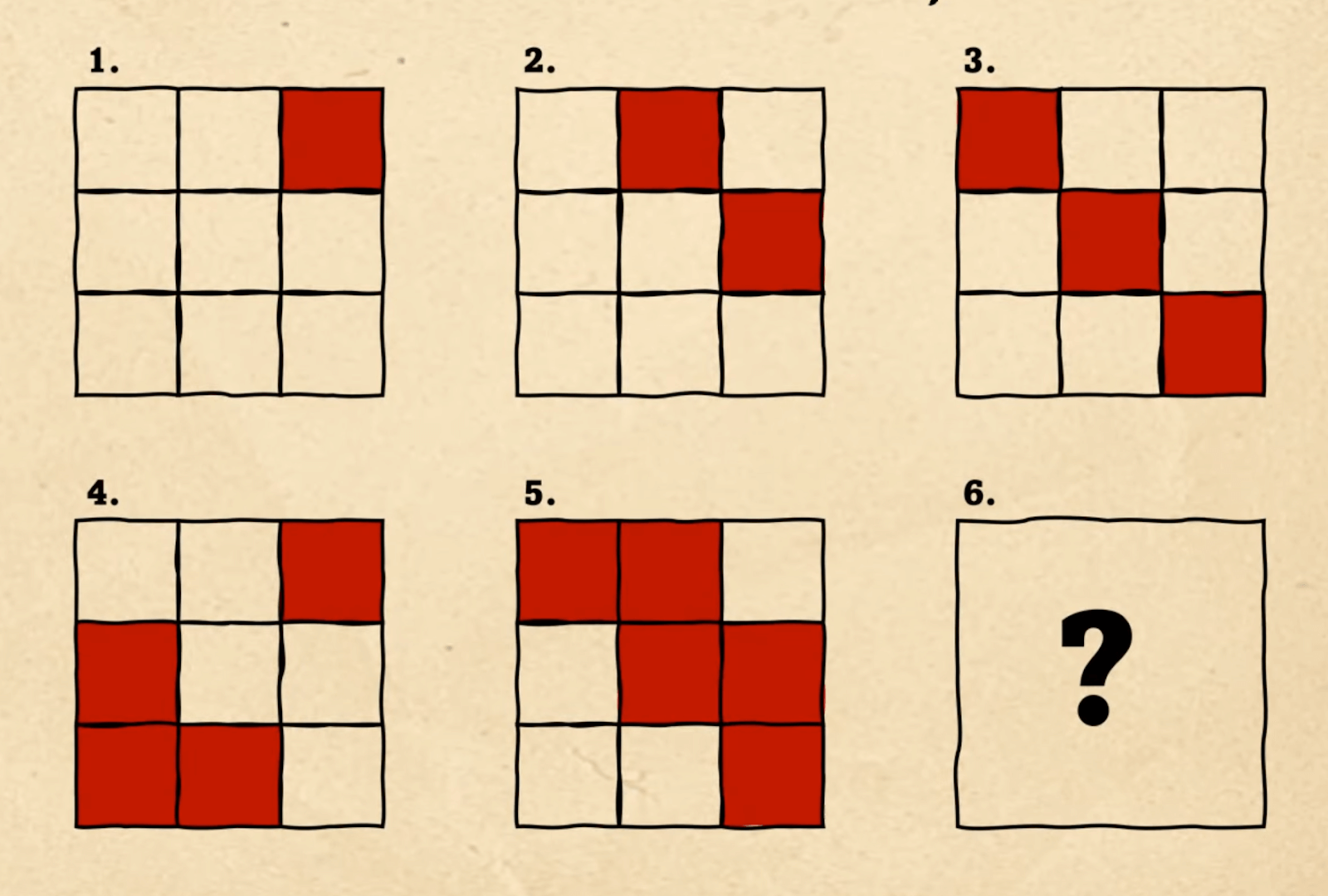
Первое, что можно заметить — что количество красных клеток в фигурах на каждом этапе увеличивается на единицу: на первом рисунке она одна, на втором две и так далее. Для наглядности поместим их рядом с фигурами:
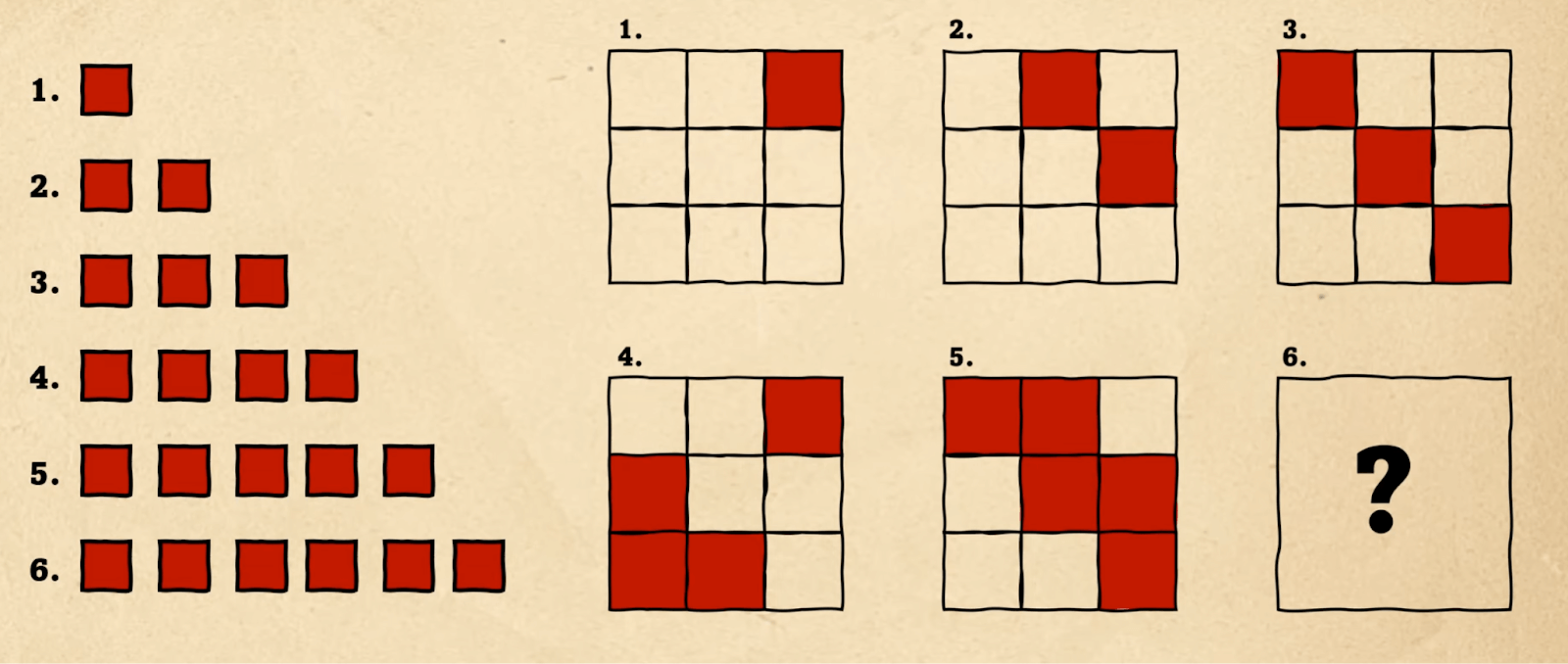
Дальше мы видим, что первые три фигуры заполняются красными клетками как бы по диагонали, слева направо. Используем это и расширим шаблон на все остальные клетки:

С первой фигурой всё просто — ставим красный квадрат ровно на первую диагональную линию:
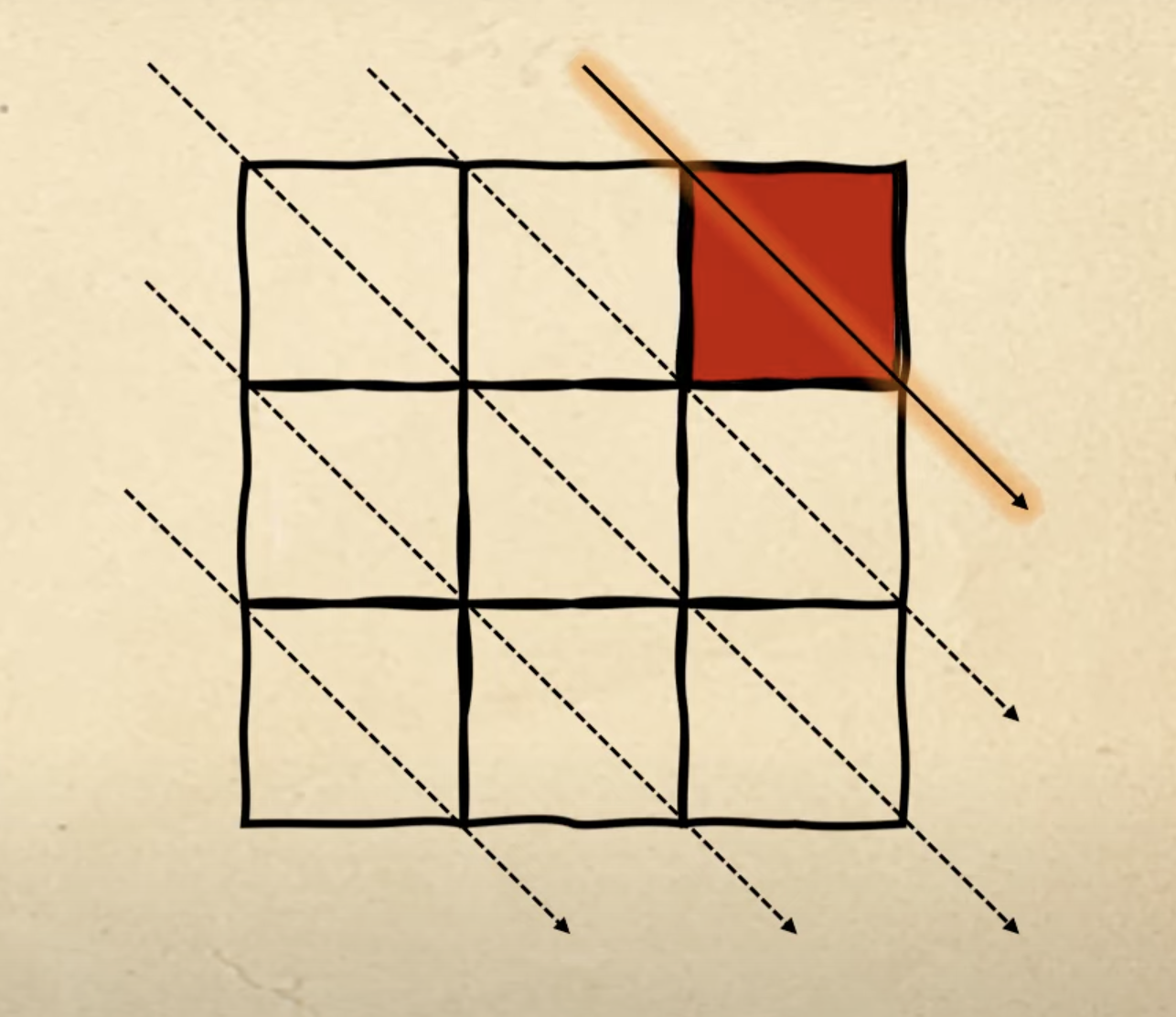
Следующая свободная диагональ, на которой мы закончили, — вторая, поэтому второй фигурой заполняем её:
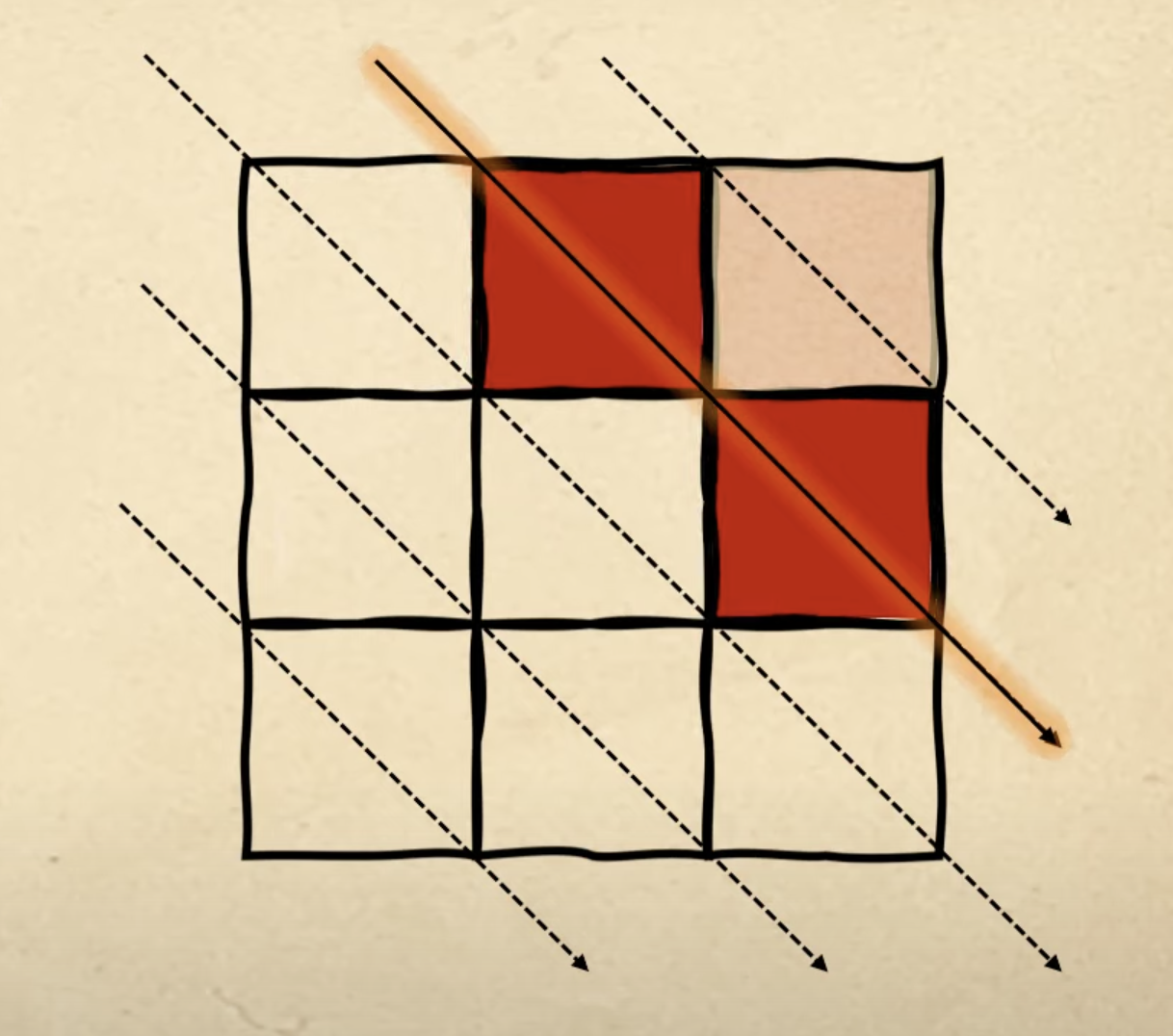
С третьей фигурой тоже всё удачно: мы закончили на второй диагонали, поэтому начинаем новую фигуру заполнять с третьей:
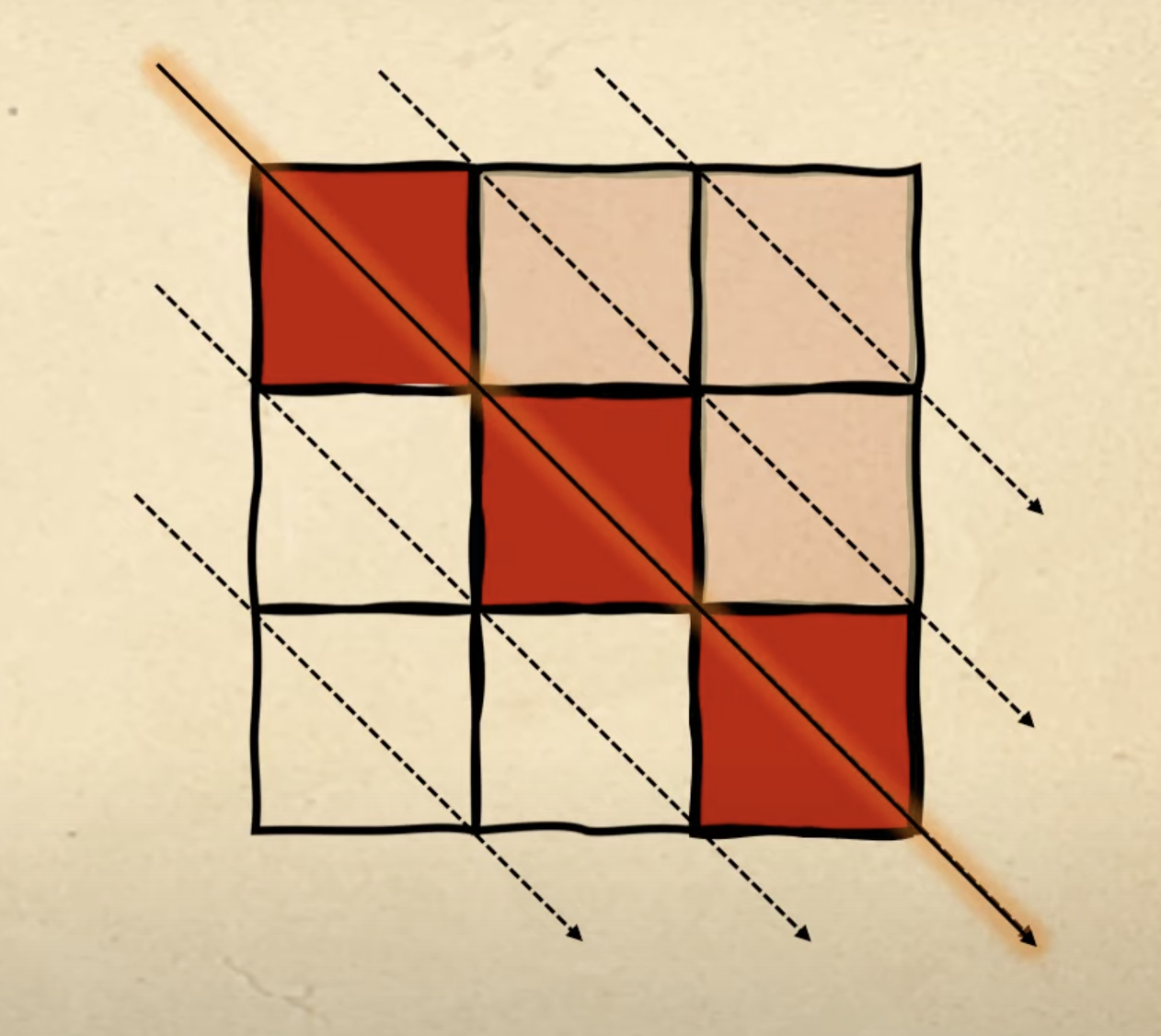
На прошлом шаге мы использовали третью диагональ, поэтому начинаем с четвёртой. Но с ней всё сложнее: на ней всего две клетки, а нам нужно разместить четыре красных квадрата:
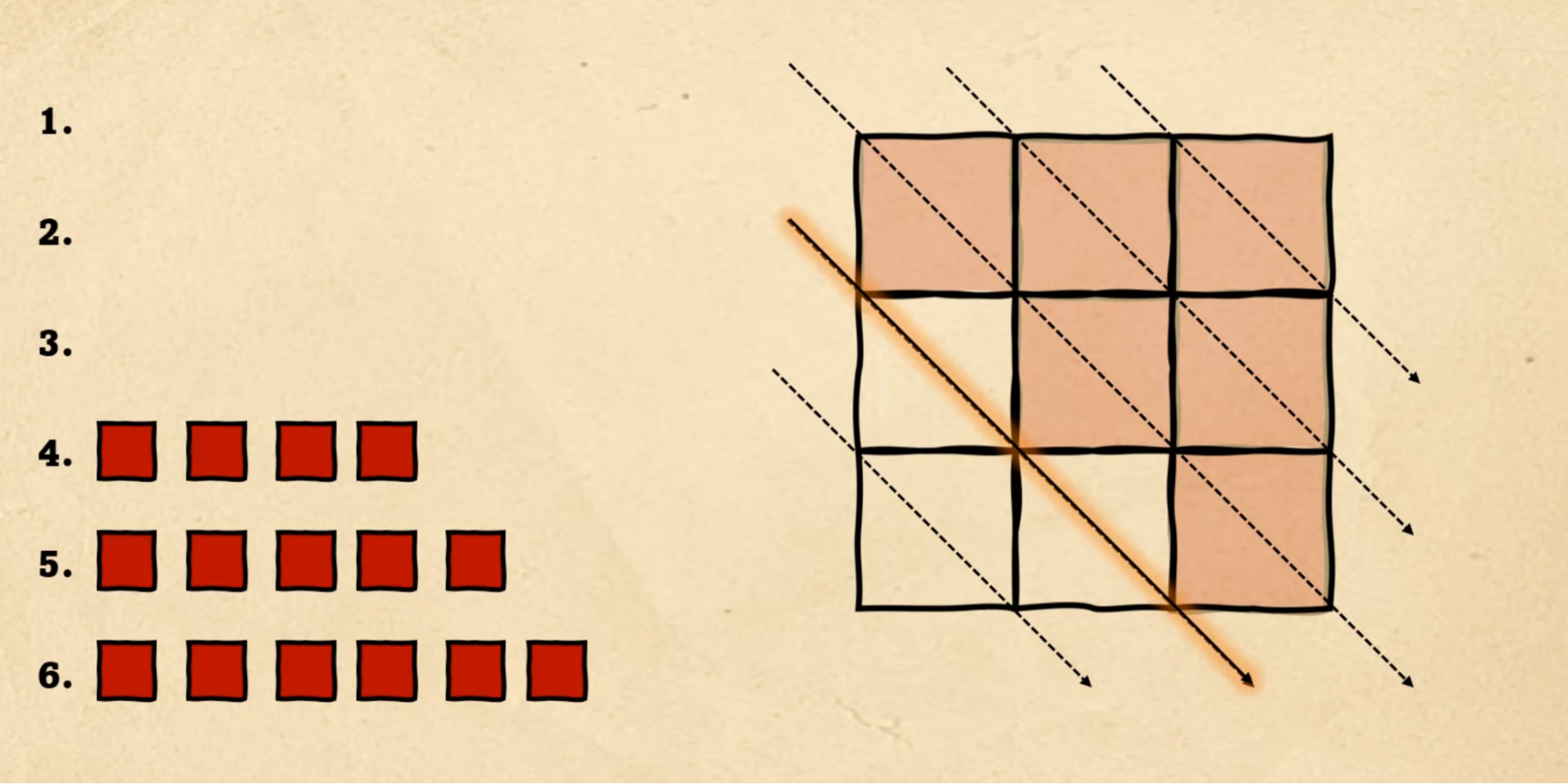
Тогда мы заполняем всю четвёртую диагональ двумя красными квадратами и переходим на пятую — туда, где станет всего один красный квадрат:
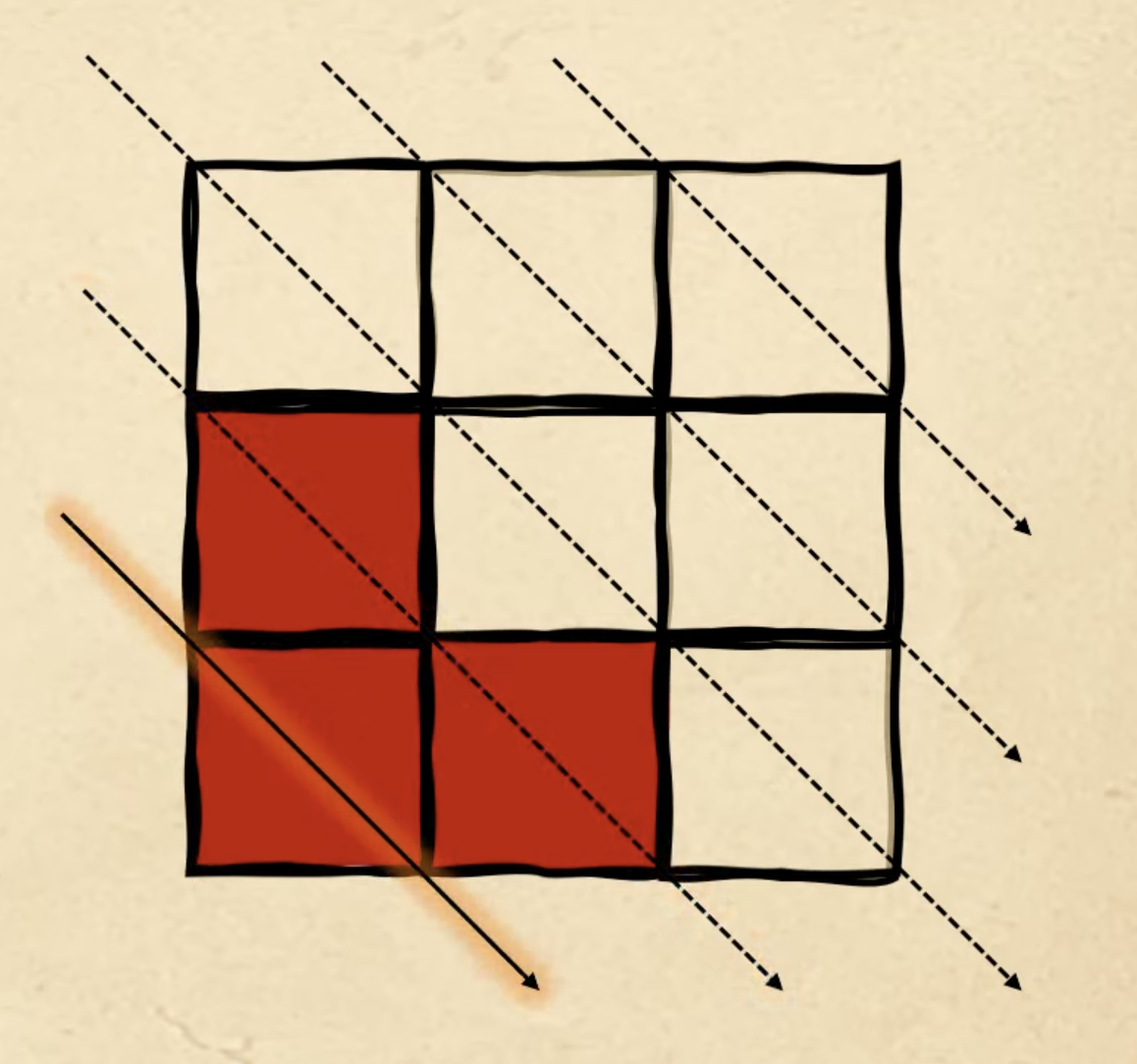
Но мы разместили на фигуре три красных квадрата, а нам нужно четыре. Возвращаемся к самому началу, к первой диагонали, и ставим туда четвёртый красный квадрат — в итоге получаем как раз нужную нам четвёртую фигуру:
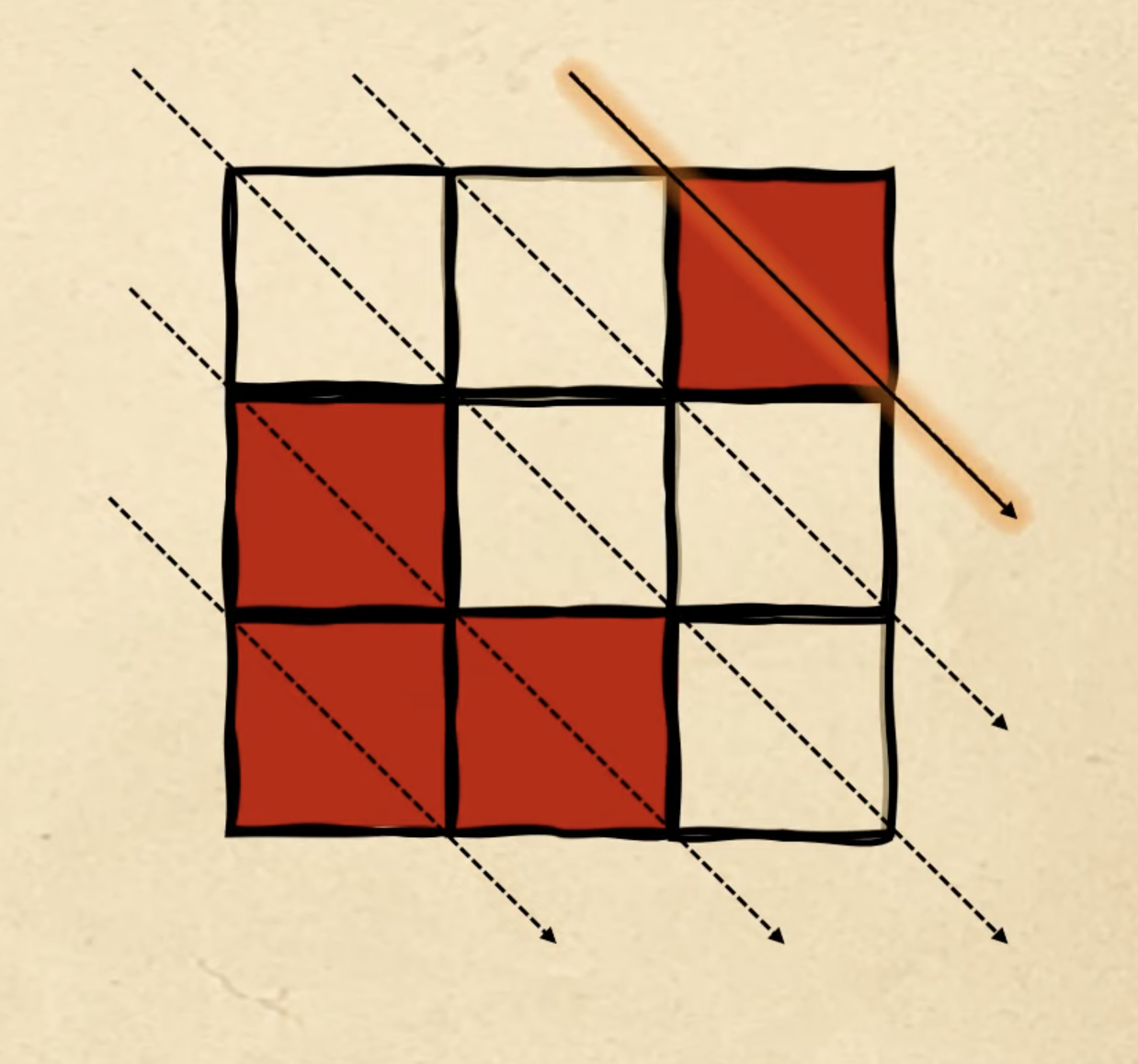
Раз мы пошли заполнять диагонали по второму кругу, придерживаемся того же принципа: начинаем с первой свободной диагонали, которую мы не использовали в прошлый раз. В четвёртой фигуре мы остановились на первой диагонали, поэтому в пятой фигуре начинаем со второй:
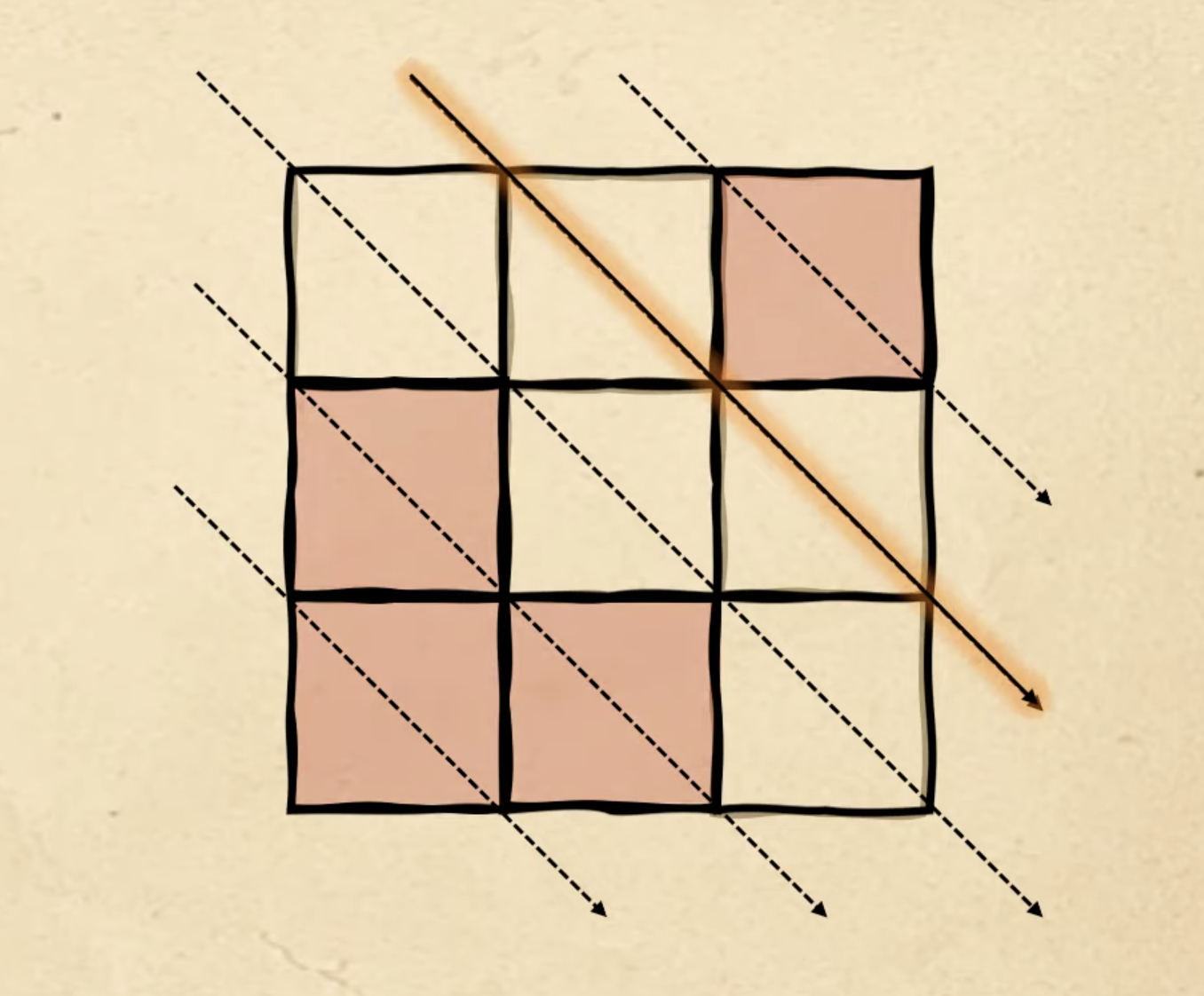
Ставим сюда два красных квадрата:
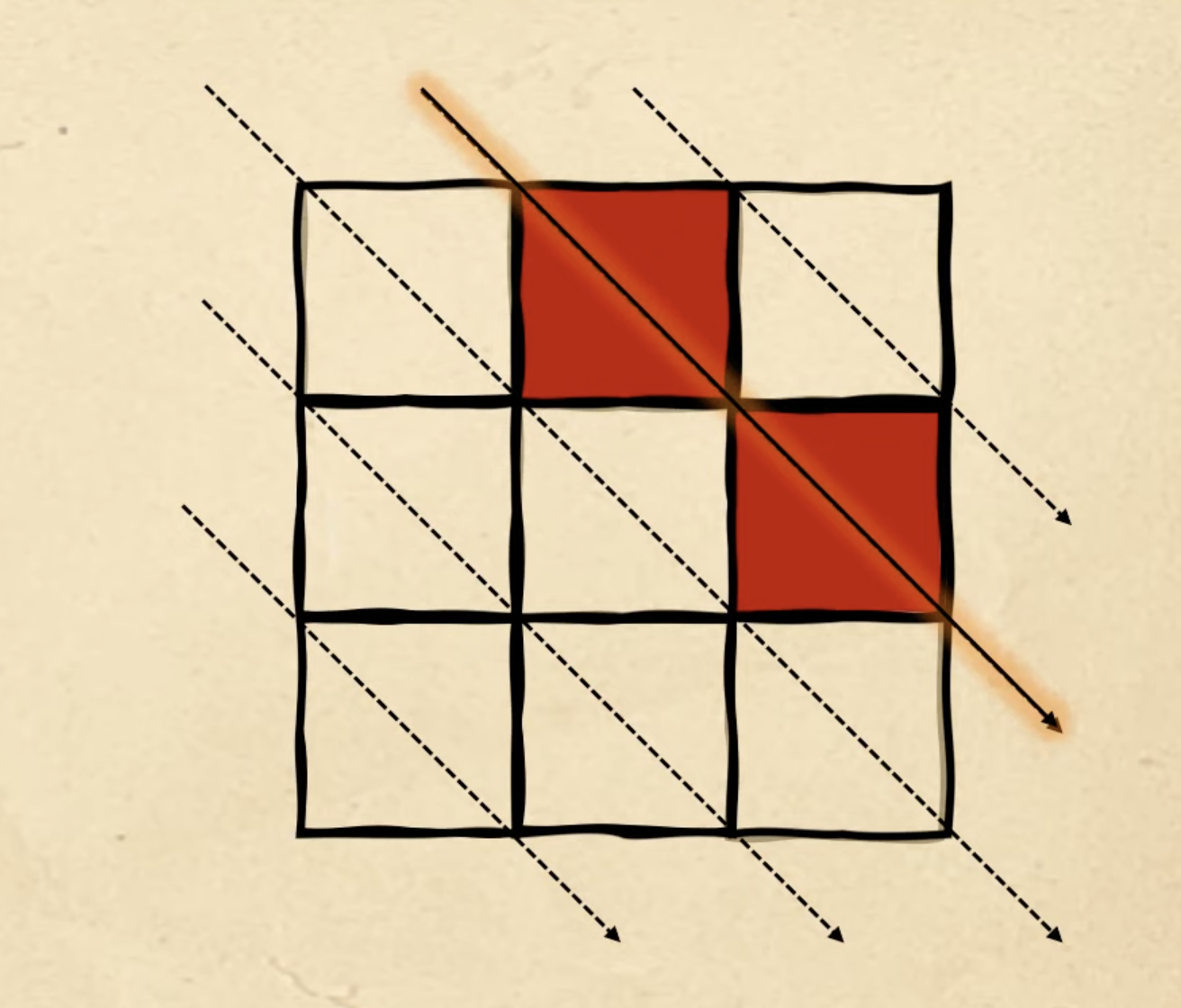
Нам нужно поставить пять квадратов, а у нас ещё осталось три. Переходим на следующую диагональ и заполняем там оставшиеся три красных квадрата — и получаем пятую фигуру из задачи:
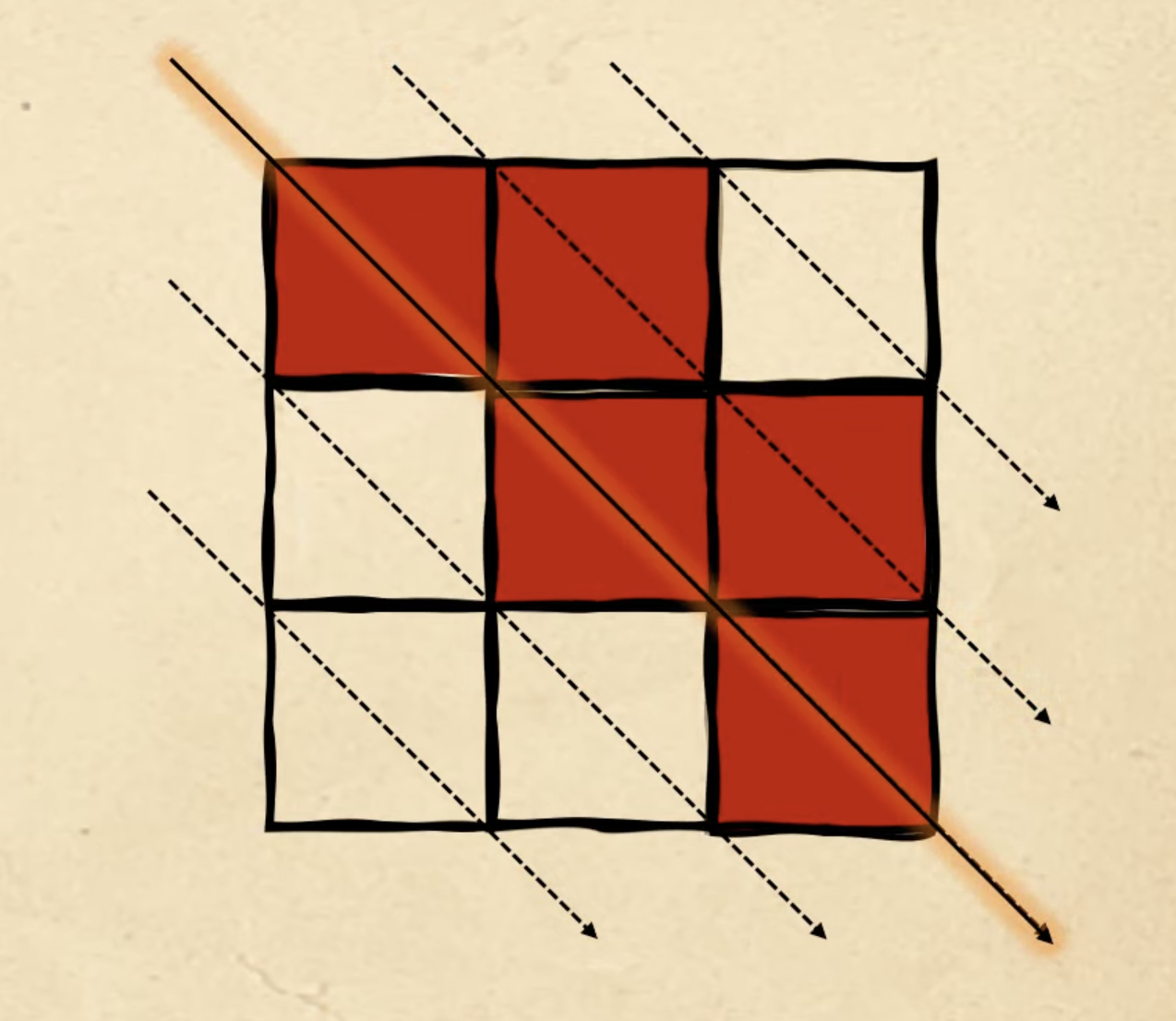
Наконец, переходим к шестой — той, что нам нужно найти. В пятой фигуре мы закончили на третьей диагонали, поэтому теперь начинаем с четвёртой:
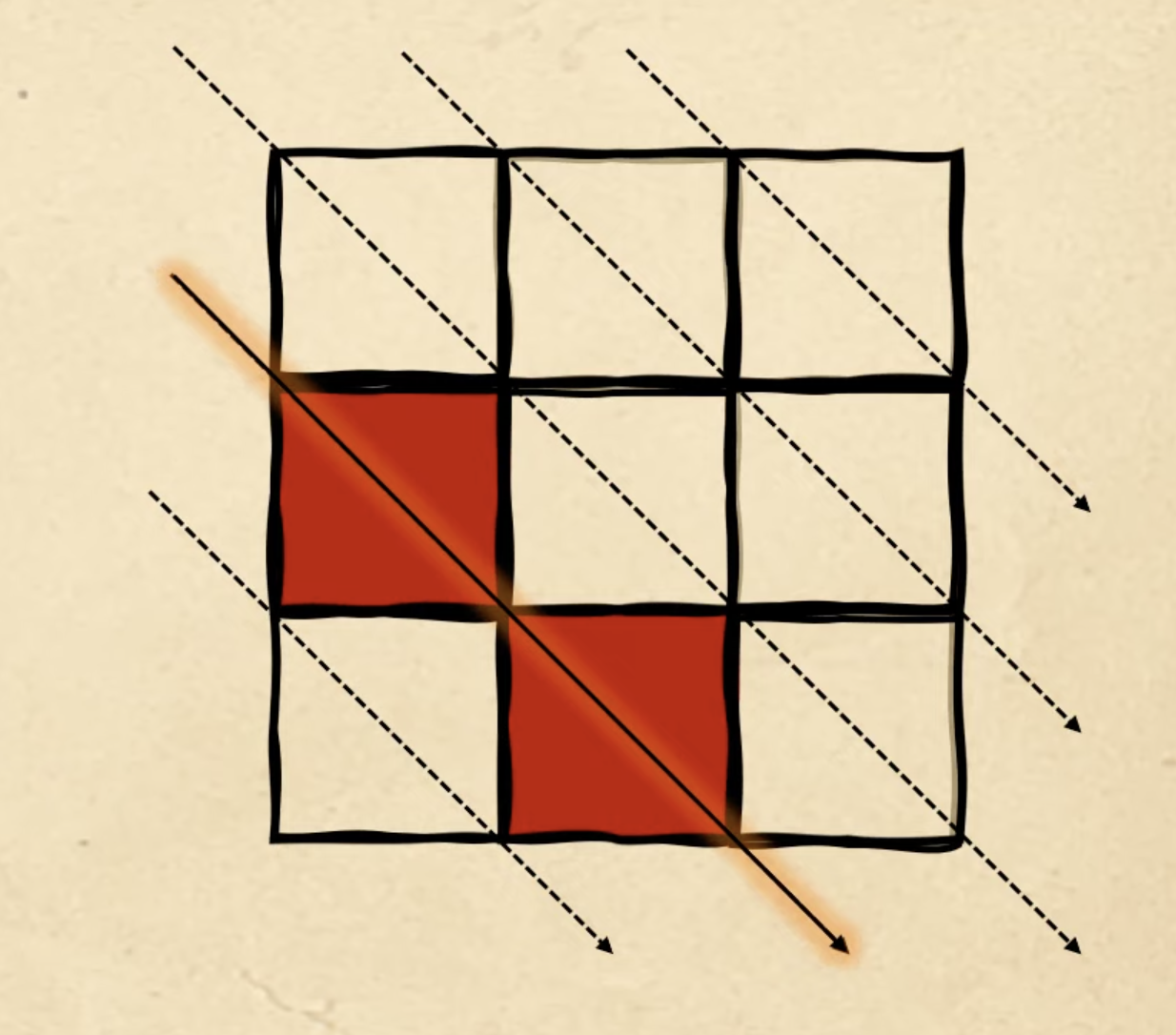
По этому же алгоритму заполняем пятую диагональ:
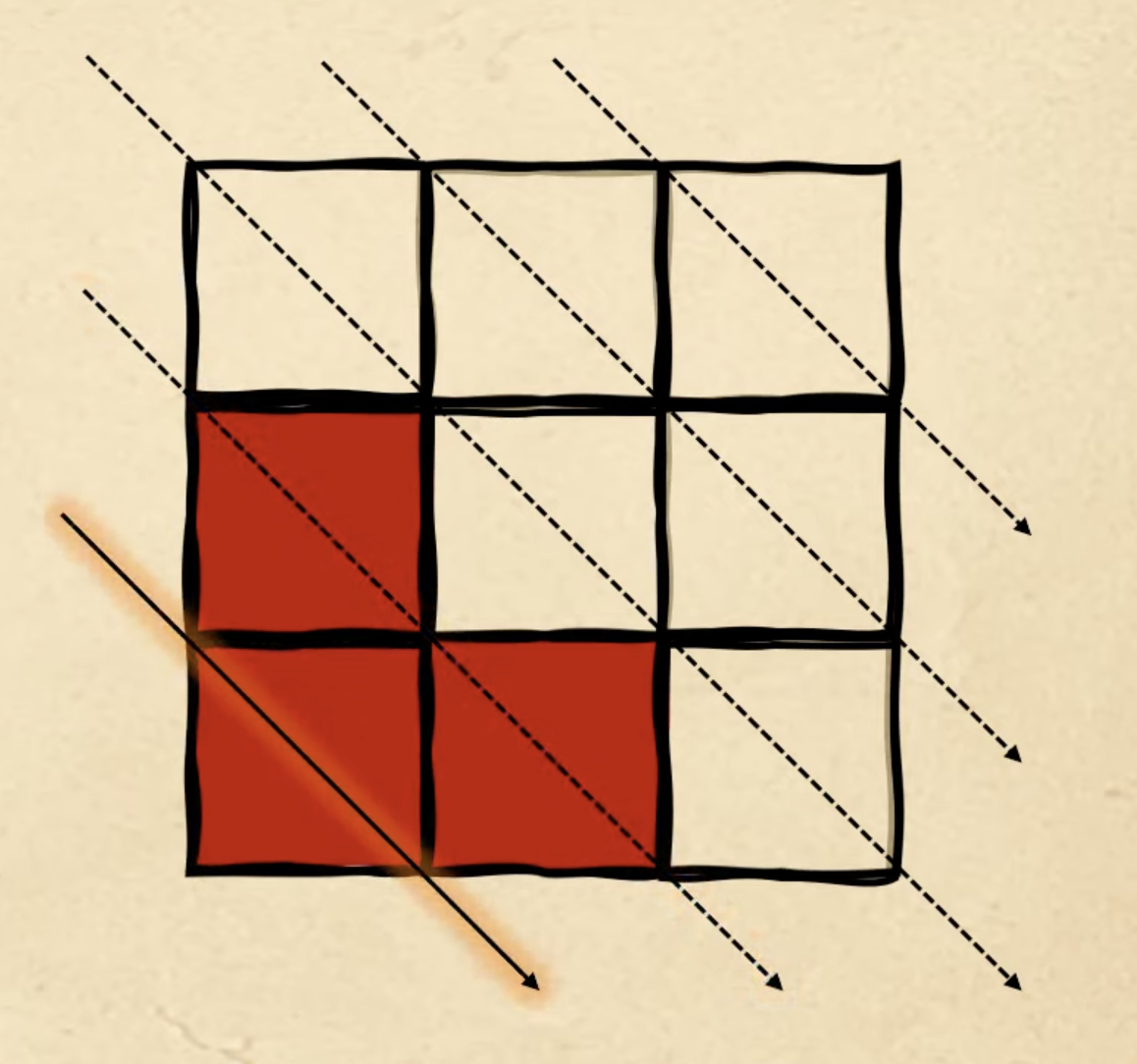
Но у нас ещё есть три красных квадрата, поэтому возвращаемся снова к первой диагонали и начинаем заполнять их оттуда:
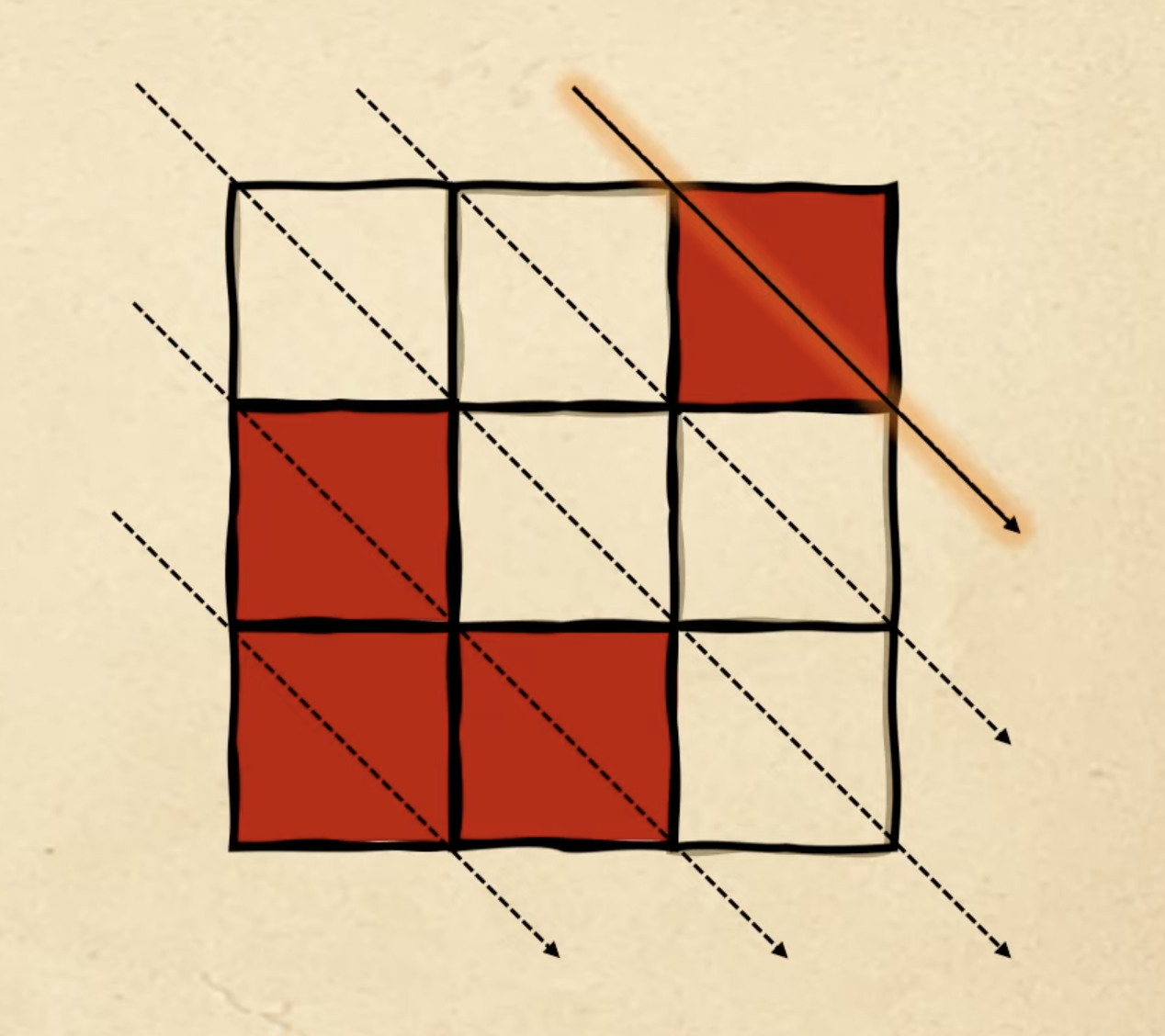
И в завершение используем вторую диагональ, чтобы поставить оставшиеся два красных квадрата. Это и будет шестая фигура:
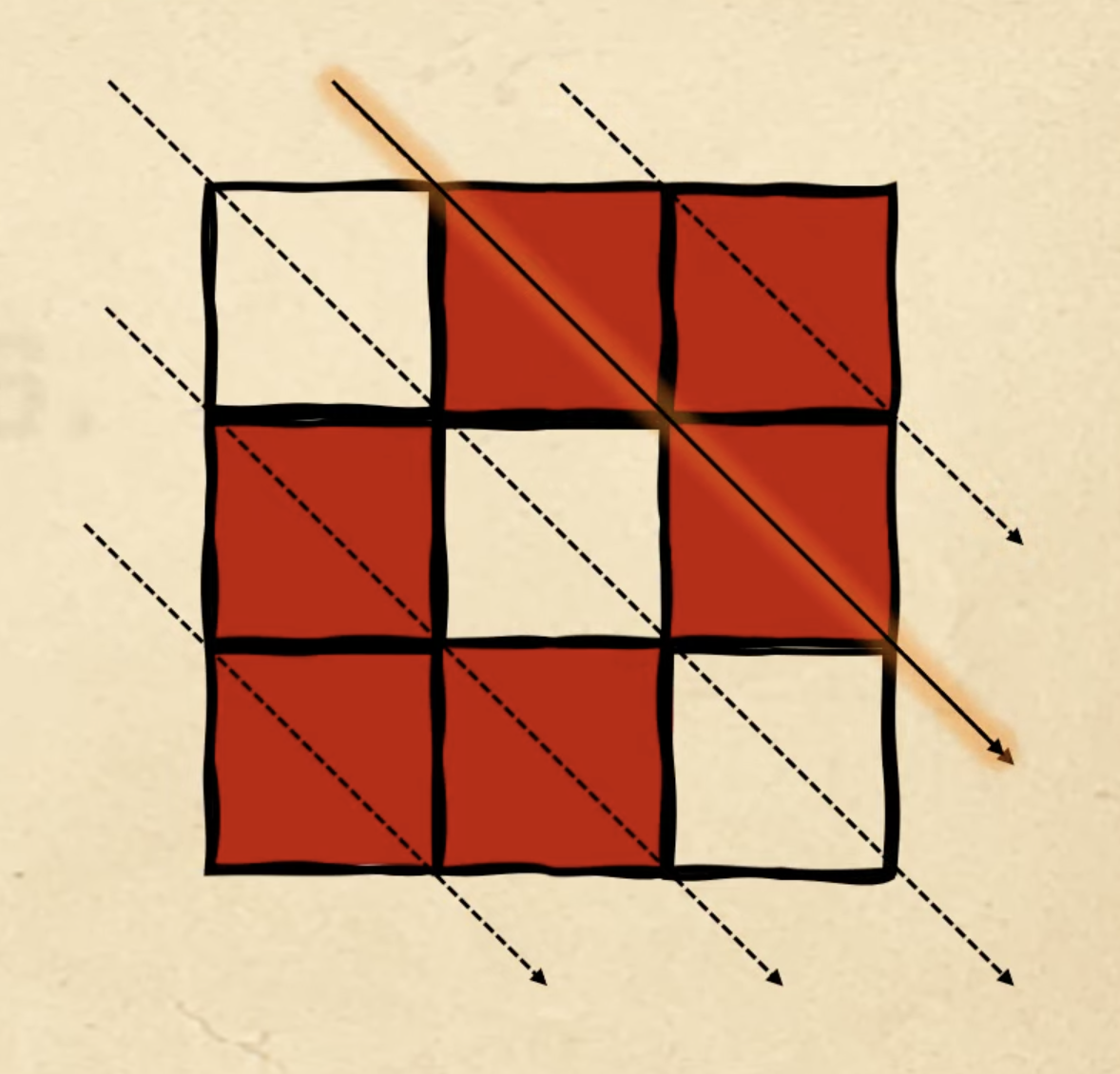
Теперь, когда вы решили задачу и поняли алгоритм, попробуйте найти 7-ю, 8-ю и 9-ю фигуру и поделитесь результатами в комментариях.
Школьная задача про числа, которую решат не все взрослые
Простая школьная задача: есть числа 6, 6, 2, 2, 8, 8, 0, 0, 0. Из них нужно составить четыре числа: одно-, двух- и трёхзначное, которые в сумме дают четвёртое трёхзначное.
Звучит просто, но с ответом могут быть сложности. Попробуйте решить эту задачку сами, а ответом поделитесь в комментариях.
Начнём с того, что представим нашу задачу визуально:

Теперь подберём варианты, при которых сумма чисел над чертой совпадёт с числом под ней. Представим, что трёхзначные числа начинаются с одной и той же цифры:
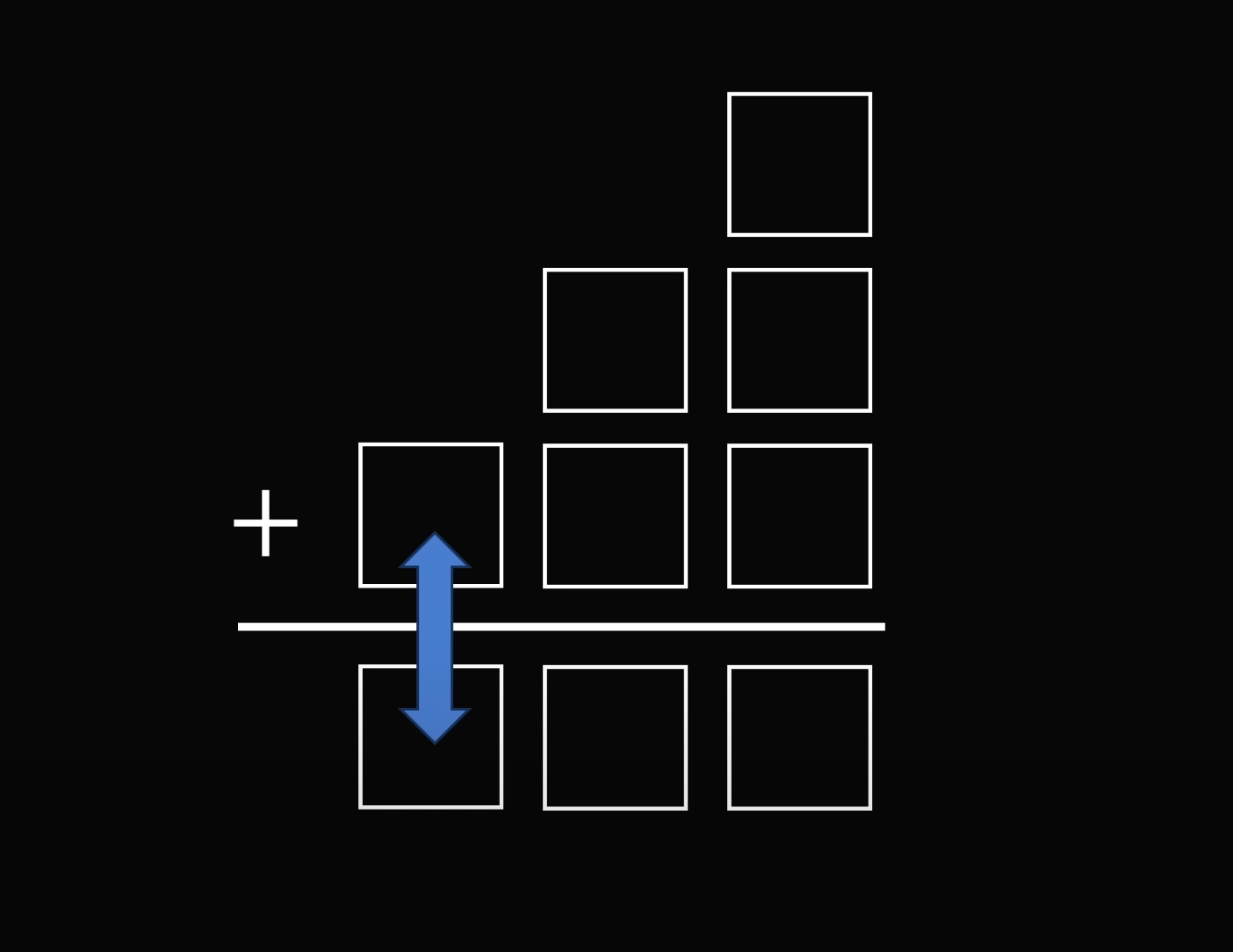
Попробуем подставить на её место шестёрку:
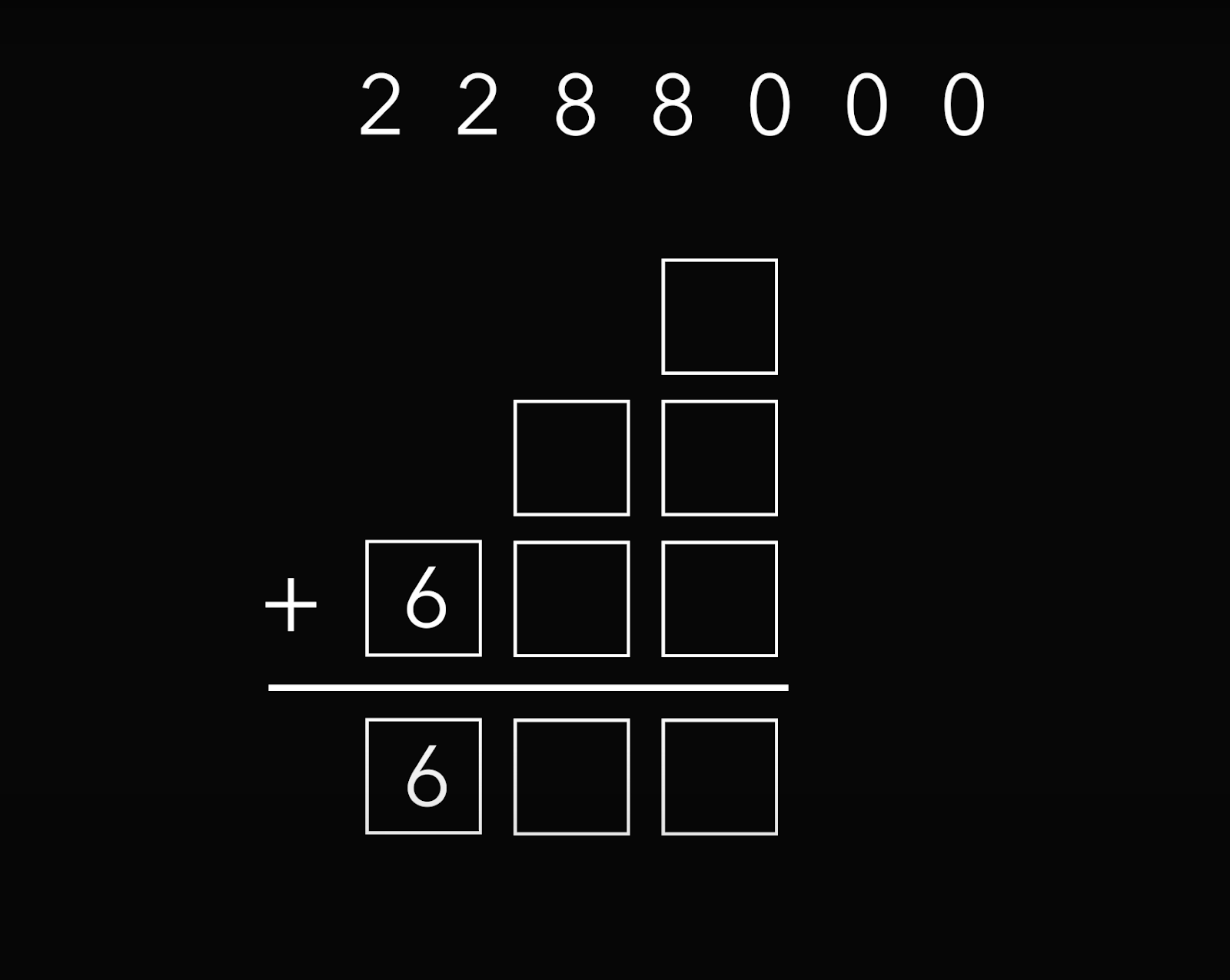
Теперь посмотрим на средний столбик:
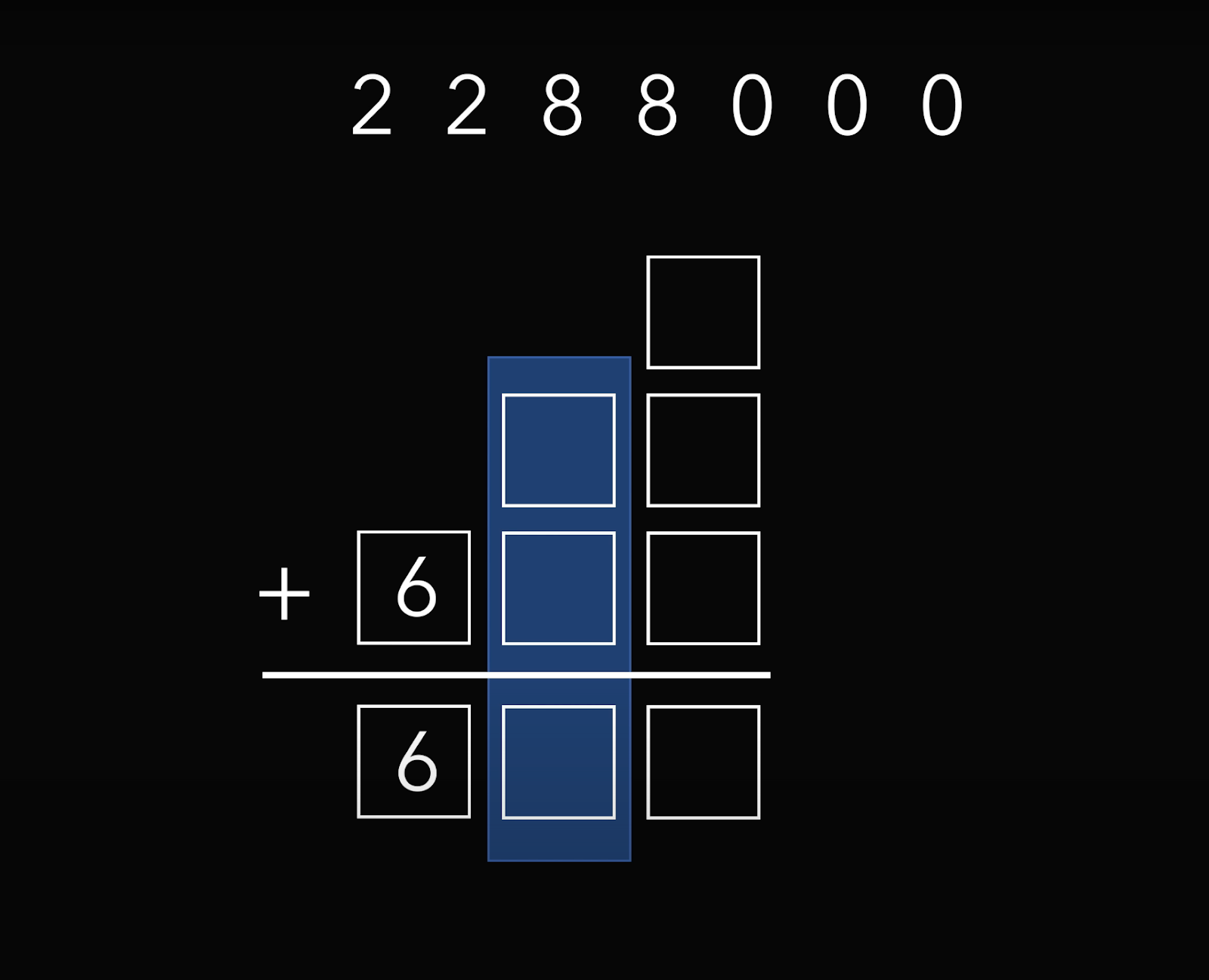
Подставим в них двойку и ноль над чертой и двойку под чертой. Это удовлетворяет нашему условию:
2 + 0 = 2

У нас остались две восьмёрки и два нуля и четыре пустые ячейки:
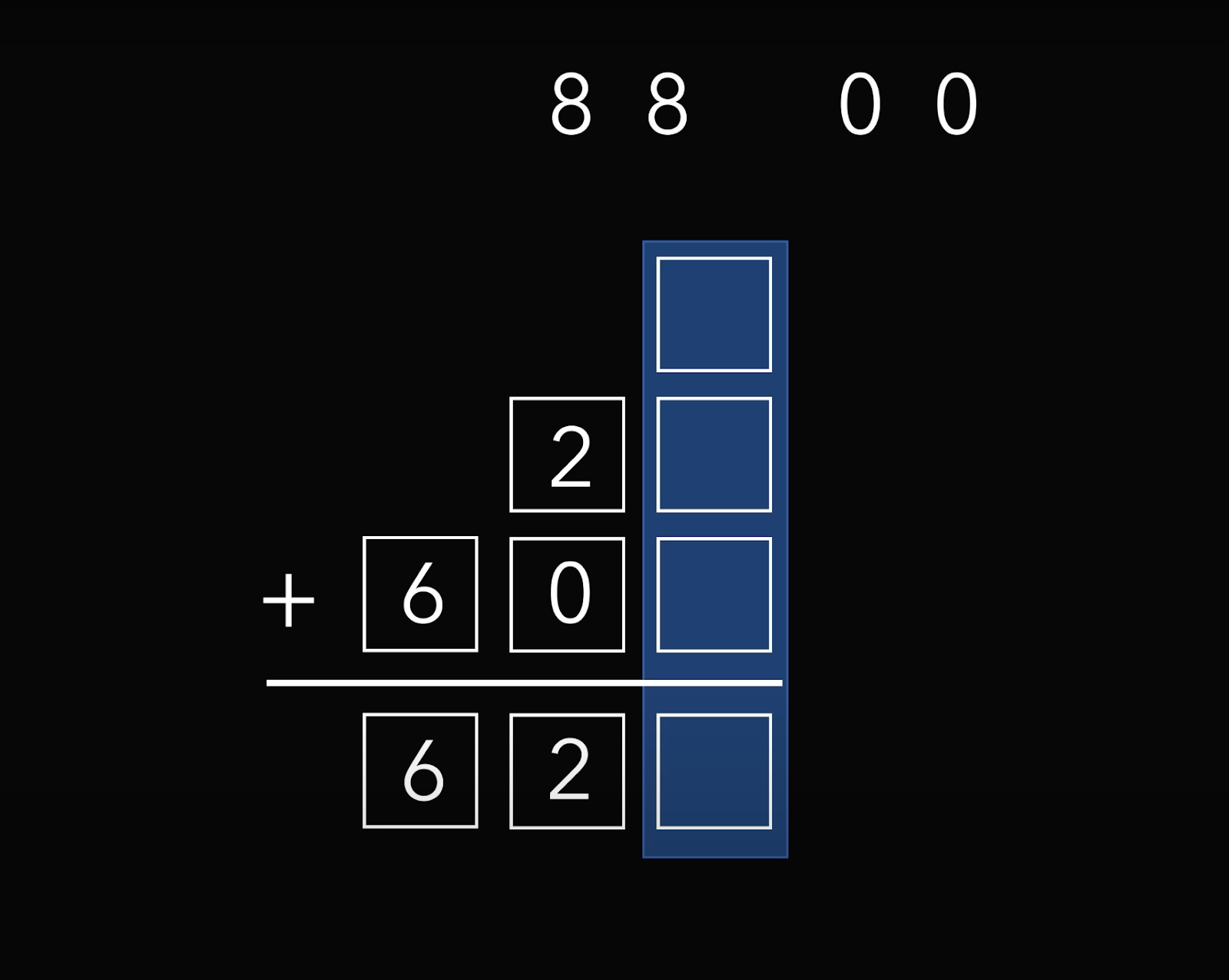
Распределим цифры так, чтобы сумма совпадала:
8 + 0 + 0 = 8
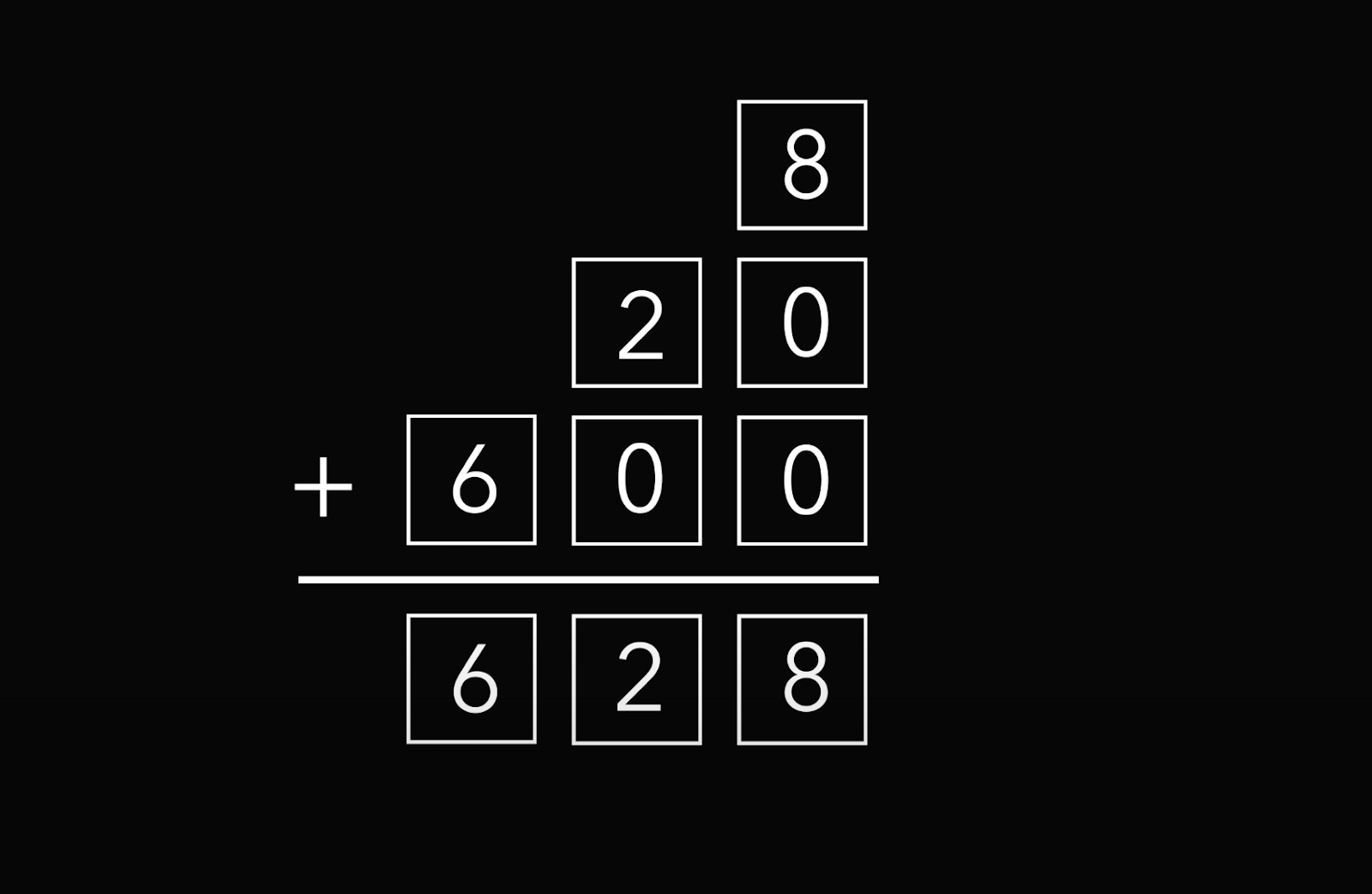
Проверяем, всё сходится:
8+ 20 + 600 = 628
Но это не единственное решение. Если присмотреться и подумать, можно найти ещё комбинации чисел, которые дадут также верную сумму. Попробуйте найти их все, теперь уже самостоятельно (и их не так много, как кажется)
Чтобы не перебирать все варианты чисел вручную, поручим это компьютеру. Для этого поступим так:
- Соберём все доступные числа в один список.
- Найдём все доступные перестановки этого списка. То, что они будут повторяться из-за одинаковых чисел, — ничего страшного, с этим разберёмся позже.
- Теперь будем перебирать все получившиеся перестановки по очереди.
- Первая цифра из очередной перестановки будет означать первое число, вторые две — второе, следующие три — третье и оставшиеся три числа сформируют результат.
- Сложим полученные числа и сравним с результатом. Если одно равно другому — мы нашли решение, выводим его на экран.
- Параллельно с этим посчитаем, сколько всего решений у нас получится.
Теперь о числах. По условию у нас складывается одно-, двух- и трёхзначное число. Можно долго спорить о том, считается ли число с нулём в начале, например, двузначным или трёхзначным, но мы решили так: не считается. Из этого и будем исходить в коде.
Для решения используем Python — в нём уже есть готовая библиотека для получения перестановок.
Как установить Python на компьютер и начать на нём писать
Прежде всего подключаем библиотеку, которая поможет нам с перестановками:
# модуль для быстрого получения всех перестановок
import itertools
Теперь заполняем стартовыми значениями нужные переменные:
# все числа из задачи
numbers = [6,6,2,2,8,8,0,0,0]
# общее количество найденных решений
count = 0
# проверенные комбинации
tested = []
# получаем все перестановки всех чисел
numbers_perm = list(itertools.permutations(numbers))Перед тем как делать цикл, подсветим два момента:
- Перед тем как составить второе и третье число, мы проверяем, первое число там ноль или нет. Если в одной из них ноль — ничего не делаем и сразу переходим к следующей перестановке. Если не ноль — всё в порядке, собираем числа. Число с результатом проверяем точно так же.
- У нас повторяются числа внутри списка, поэтому при перестановке может получиться так, что просто поменяются местами две первые шестёрки. Для компьютера это разные перестановки, для нас — нет. Чтобы избежать повторов в решении, добавим список с проверенными перестановками. Как только нашли очередное решение — заносим эту перестановку в список, а в самом начале цикла будем проверять, есть ли текущая комбинация в этом списке или нет. Если она там есть — переходим сразу к следующей, чтобы не повторяться.
Учитывая всё это, пишем основной цикл:
# перебираем все перестановки по очереди
for i in range(len(numbers_perm)):
# если такую перестановку мы уже проверяли — переходим сразу к следующей итерации цикла
if numbers_perm[i] in tested:
continue
# получаем первое число
first = numbers_perm[i][0]
# если первая цифра второго числа — ноль, то переходим к следующей итерации цикла
if numbers_perm[i][1] == 0:
continue
# получаем второе число
second = 10 * numbers_perm[i][1] + numbers_perm[i][2]
# точно так же собираем третье число
if numbers_perm[i][3] == 0:
continue
third = 100 * numbers_perm[i][3] + 10 * numbers_perm[i][4] + numbers_perm[i][5]
# и собираем результат
if numbers_perm[i][6] == 0:
continue
result = 100 * numbers_perm[i][6] + 10 * numbers_perm[i][7] + numbers_perm[i][8]
# если сумма получается верной
if first + second + third == result:
# выводим найденное решение на экран
print(str(first) + ' + ' + str(second) + ' + ' + str(third) + ' = ' + str(result))
# увеличиваем количество найденных решений на единицу
count = count + 1
# добавляем проверенную комбинацию в список
tested.append(numbers_perm[i])Последнее, что нам осталось сделать, — вывести общее количество найденных решений:
# выводим общее количество найденных решений
print('Всего решений: ' + str(count))
Запустите код, чтобы узнать, сколько же на самом деле решений имеет задача и каких. А потом сравните это с тем, что получилось у вас, когда вы решали эту задачу без кода.
# модуль для быстрого получения всех перестановок
import itertools
# все числа из задачи
numbers = [6,6,2,2,8,8,0,0,0]
# общее количество найденных решений
count = 0
# проверенные комбинации
tested = []
# получаем все перестановки всех чисел
numbers_perm = list(itertools.permutations(numbers))
# перебираем все перестановки по очереди
for i in range(len(numbers_perm)):
# если такую перестановку мы уже проверяли — переходим сразу к следующей итерации цикла
if numbers_perm[i] in tested:
continue
# получаем первое число
first = numbers_perm[i][0]
# если первая цифра второго числа — ноль, то переходим к следующей итерации цикла
if numbers_perm[i][1] == 0:
continue
# получаем второе число
second = 10 * numbers_perm[i][1] + numbers_perm[i][2]
# точно так же собираем третье число
if numbers_perm[i][3] == 0:
continue
third = 100 * numbers_perm[i][3] + 10 * numbers_perm[i][4] + numbers_perm[i][5]
# и собираем результат
if numbers_perm[i][6] == 0:
continue
result = 100 * numbers_perm[i][6] + 10 * numbers_perm[i][7] + numbers_perm[i][8]
# если сумма получается верной
if first + second + third == result:
# выводим найденное решение на экран
print(str(first) + ' + ' + str(second) + ' + ' + str(third) + ' = ' + str(result))
# увеличиваем количество найденных решений на единицу
count = count + 1
# добавляем проверенную комбинацию в список
tested.append(numbers_perm[i])
# выводим общее количество найденных решений
print('Всего решений: ' + str(count)) Сложная задача по простой математике для взрослых
Сложная задача по простой математике для взрослых Взрослая задача про монеты со сложными условиями
Взрослая задача про монеты со сложными условиями Две задачи про монеты для людей с нестандартным мышлением
Две задачи про монеты для людей с нестандартным мышлением Задача про границы, где вам нужно выйти за них, чтобы её решить
Задача про границы, где вам нужно выйти за них, чтобы её решить Самая сложная задача для школьников, которую никто не смог решить
Самая сложная задача для школьников, которую никто не смог решить Задача на логику: что в какой коробке?
Задача на логику: что в какой коробке?Сто программистов и сложный карьерный рост
В одной большой ИТ-компании работает сто программистов. В закрытой комнате в ста пронумерованных коробках случайным образом размещены карточки с номерами от 1 до 100. Программисты могут зайти в комнату по одному и открыть 50 коробок в поисках своего номера. После того как номер найден или открыта 50-я коробка, программист должен покинуть комнату.
Если свои номера найдут все сто программистов, их всех повысят. Но если хотя бы один из них не сможет найти свой номер, будут уволены все сто программистов.
Посетив комнату, программисты не могут общаться с теми, кто в ней ещё не был. Но они могут обсуждать общую стратегию до того, как попадут в комнату. Какая стратегия поисков будет наилучшей, чтобы всех программистов повысили, а не уволили?
Если программисты будут искать свой номер бессистемно, вероятность успеха каждого из них составит 50%. Тогда вероятность, что все найдут свои номера, будет слишком мала:
В = (1/2)100 = 1/1267650600228229401496703205376 = 0,0000000000000000000000000000008
Но что, если все программисты договорятся открывать коробки, начиная со своего номера и до тех пор, пока не найдут карточку, которая будет вести на исходную коробку? Представим, что в комнату вошёл программист с номером 50 и ищет свой номер таким образом:
- Открывает первой коробку №50, в ней номер 99.
- Открывает коробку №99, в ней номер 69.
- Открывает коробку №69, в ней номер 97.
- Открывает коробку №97, в ней номер 22.
- Открывает коробку №22, в ней номер 2.
- Открывает коробку №2, в ней номер 39.
- Открывает коробку №39, в ней номер 3.
- Открывает коробку №3, в ней номер 15.
- Открывает коробку №15, в ней номер 57.
- Открывает коробку №57, в ней номер 50 — номер самого программиста.
В таком случае вероятность, что все программисты найдут свои номера, вырастет до 0,31. Но почему? Сейчас объясним.
Дело в том, что номера всех программистов в пронумерованных коробках образуют какую-то зацикленную последовательность (или несколько последовательностей, но об этом позже). Простейший такой цикл может быть номером 1 в коробке №1:

Цикл чуть сложнее может состоять из двух объектов, например если в коробке №1 лежит номер 7, а в коробке №7 лежит номер 1:

Цикл может содержать три коробки, четыре и так далее. Такие зацикленные последовательности могут состоять из скольких угодно элементов. В случае с сотней коробок самая длинная последовательность может содержать их все:

Но гораздо вероятнее, что номера в сотне коробок образуют несколько зацикленных последовательностей: какие-то короче, а какие-то — длиннее:

Если открывать коробки в последовательности, при которой первая коробка будет иметь тот же номер, что и сам программист, а следующая — номер из предыдущей, есть вероятность рано или поздно найти коробку со своим номером внутри:

Но у нас есть ограничение: каждый программист может открыть только 50 коробок. Если номер программиста находится в 53-й коробке в зацикленной последовательности, программист просто не доберётся до этой коробки за отведённое число открываний.
Из этого следует, что вероятность того, что все программисты найдут свои номера по выбранной стратегии, зависит от того, есть ли в нашем множестве коробок такие последовательности, в которых 51 коробка или более. Эта вероятность равняется ⅓, но давайте в этом убедимся.
Мы можем представить зацикленную последовательность из ста коробок так:
№1 → №2 → №3 → №4 → … → №100 → №1
Но вероятнее, что последовательность будет примерно такой:
№5 → №99 → №51 → №17 → … → №63 → №5
Подойдём к процессу открывания коробок с другой стороны:
- При первом открывании мы выбираем из 100 коробок.
- При втором — из 99.
- При третьем — из 98.
… - При сотом открывании — из 1.
Получается, что общее количество вариантов перестановок номеров в коробках будет таким:
100 × 99 × 98 × … × 1 = 100!
Значит, для ста коробок у нас есть 100! вариантов образования зацикленной последовательности. При этом многие варианты фактически включают друг друга, потому что наши зацикленные последовательности имеет вид не прямых, а кругов. Например, вот эти две последовательности — одна и та же последовательность:
№5 → №99 → №51 → №17 → … → №63 → №5
№99 → №51 → №17 → … → №63 → №5 → №99
Получается, что количество уникальных зацикленных последовательностей будет равно 100!/100. Тогда вероятность того, что зацикленная последовательность будет содержать 100 коробок, можно вычислить так:
В(ЗП=100) = количество уникальных ЗП / количество перестановок = (100!/100)/100! = 1/100
Для 99 коробок вероятность будет 1/99, для 98 — 1/98 и так далее. Чтобы вычислить вероятность того, что номера в ста коробках составляют зацикленные последовательности из 50 элементов, сложим вероятности того, что эти последовательности больше: 1/51 + 1/52 + 1/53 + 1/54 … + 1/100. Получится вероятность 0,69%.

Тогда получается, что вероятность того, что номера в ста коробках образуют зацикленные последовательности из 50 и менее элементов — 0,31%:
1 — 0,69 = 0,31
И хотя 0,31 — это не так много, всё же это намного больше, чем 0,0000000000000000000000000000008.
Айтишники, мопед и летняя поездка
Андрей, Вова и Саша — три друга-айтишника. Однажды летом они решили съездить из Москвы в город Мышкин Ярославской области: там красиво и как раз проходит выставка компьютерных мышей. Ехать на поезде не хотелось, а из транспорта у них был только двухместный мопед. Но ребята молодые и спортивные и задумали план: один пойдёт пешком, а двое поедут. Стартовать из Москвы решили одновременно. За какое самое короткое время все трое доберутся до Мышкина?
Немного цифр:
- Скорость пешком — 15 км/ч.
- Скорость мопеда — 60 км/ч.
- От Москвы до Мышкина — 300 км.
Начнём с самого очевидного решения. Пусть Андрей и Вова поедут на мопеде, а Саша идёт пешком. Когда Андрей с Вовой доберутся до Мышкина, Андрей оставит там Вову и поедет обратно, в сторону Москвы, чтобы забрать Сашу:
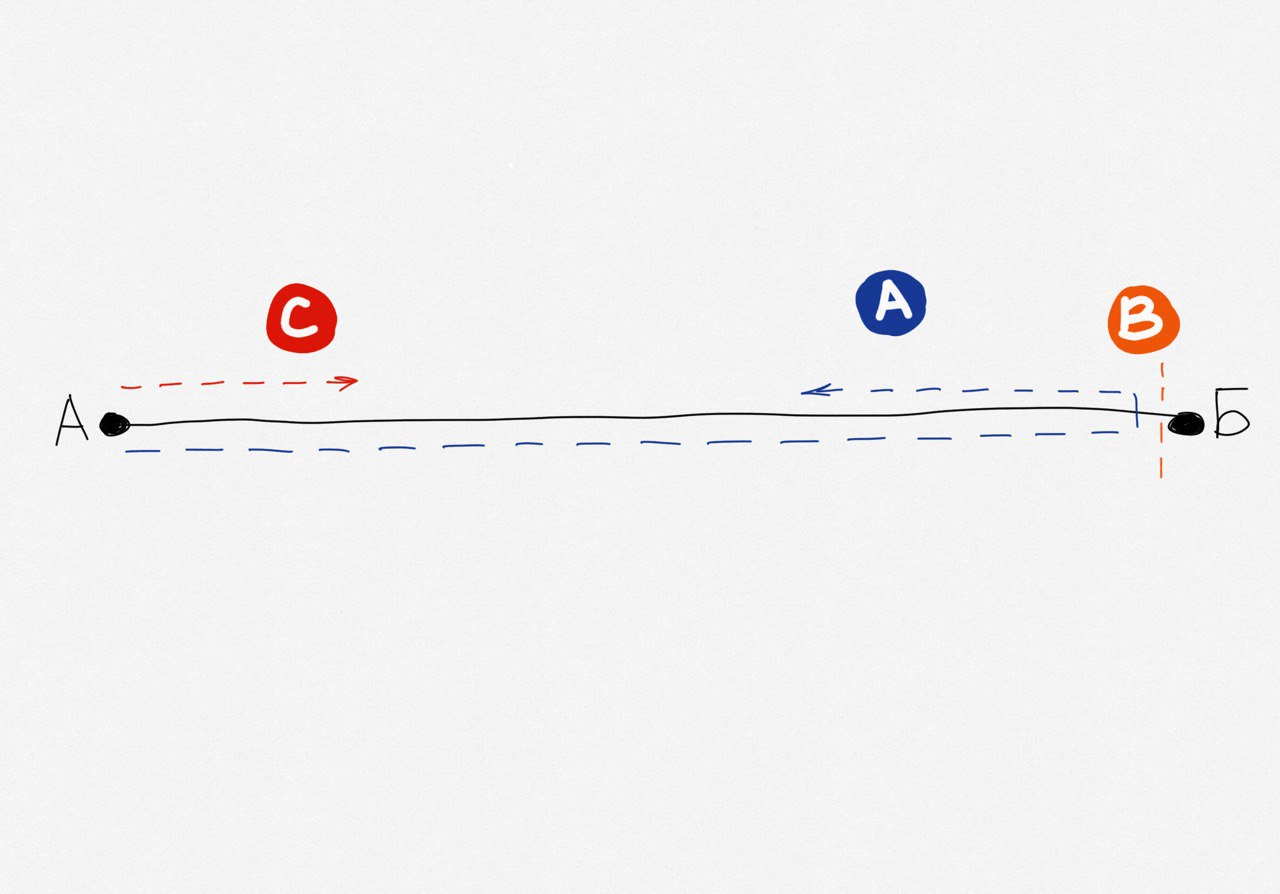
Это решение не самое оптимальное: пока Вова будет дожидаться Андрея с Сашей, он будет зря терять время и не внесёт никакого вклада в сокращение общего времени на дорогу. И если кто-либо из ребят будет ждать остальных, общее время не будет самым коротким.
Чтобы Вова мог поучаствовать в оптимизации времени, Андрею нужно оставить его недалеко от Мышкина. Тогда оставшееся расстояние Вова преодолеет пешком:
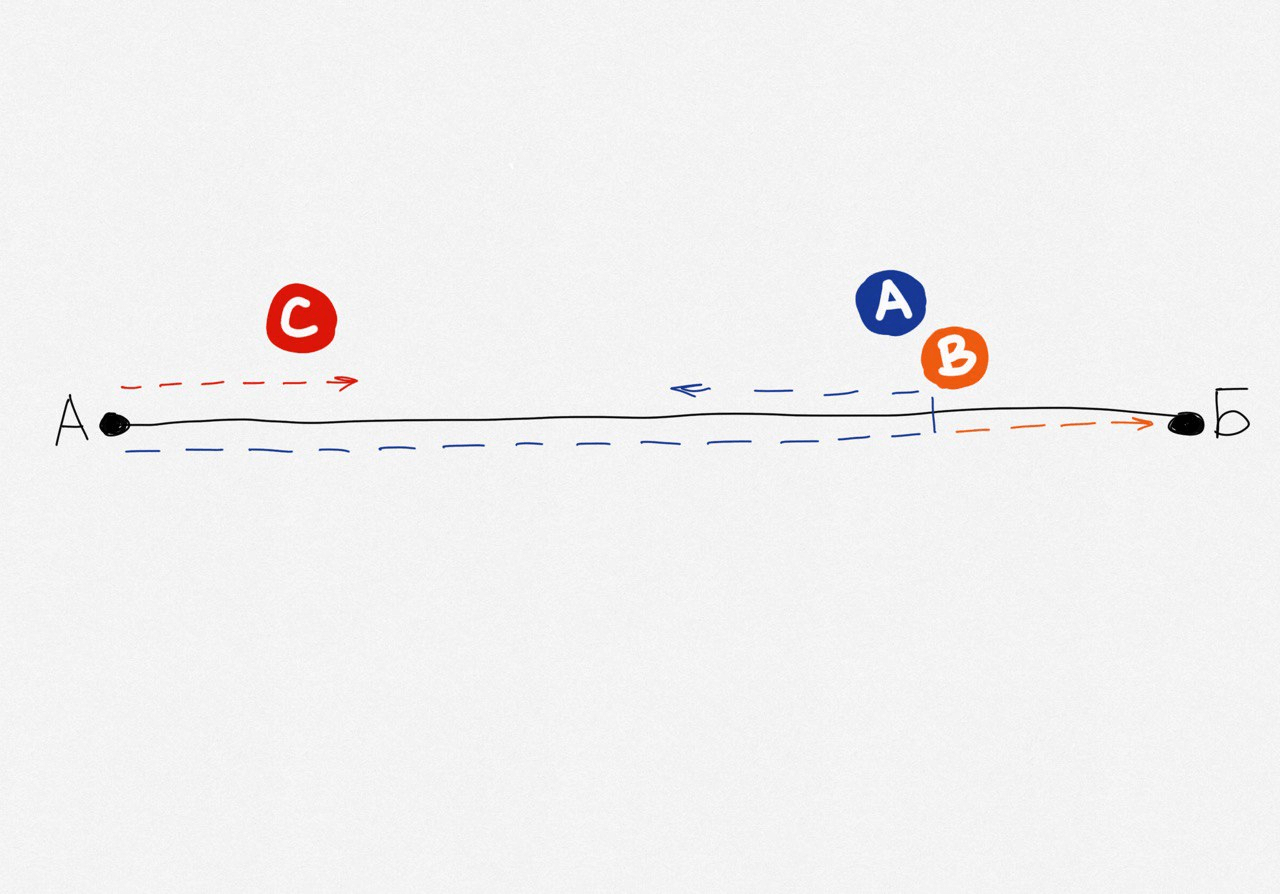
Как мы помним, общее время на дорогу может считаться самым коротким, если никто никого не дожидается. Если Вова доберётся раньше, он будет ждать Андрея с Сашей, а если позже, то Андрей и Саша будут ждать Вову.
Значит, нужно сделать так, чтобы Андрей с Сашей добрались до Мышкина одновременно с Вовой. Для этого нужно точно рассчитать точку на общем пути, где Андрей оставит Вову:
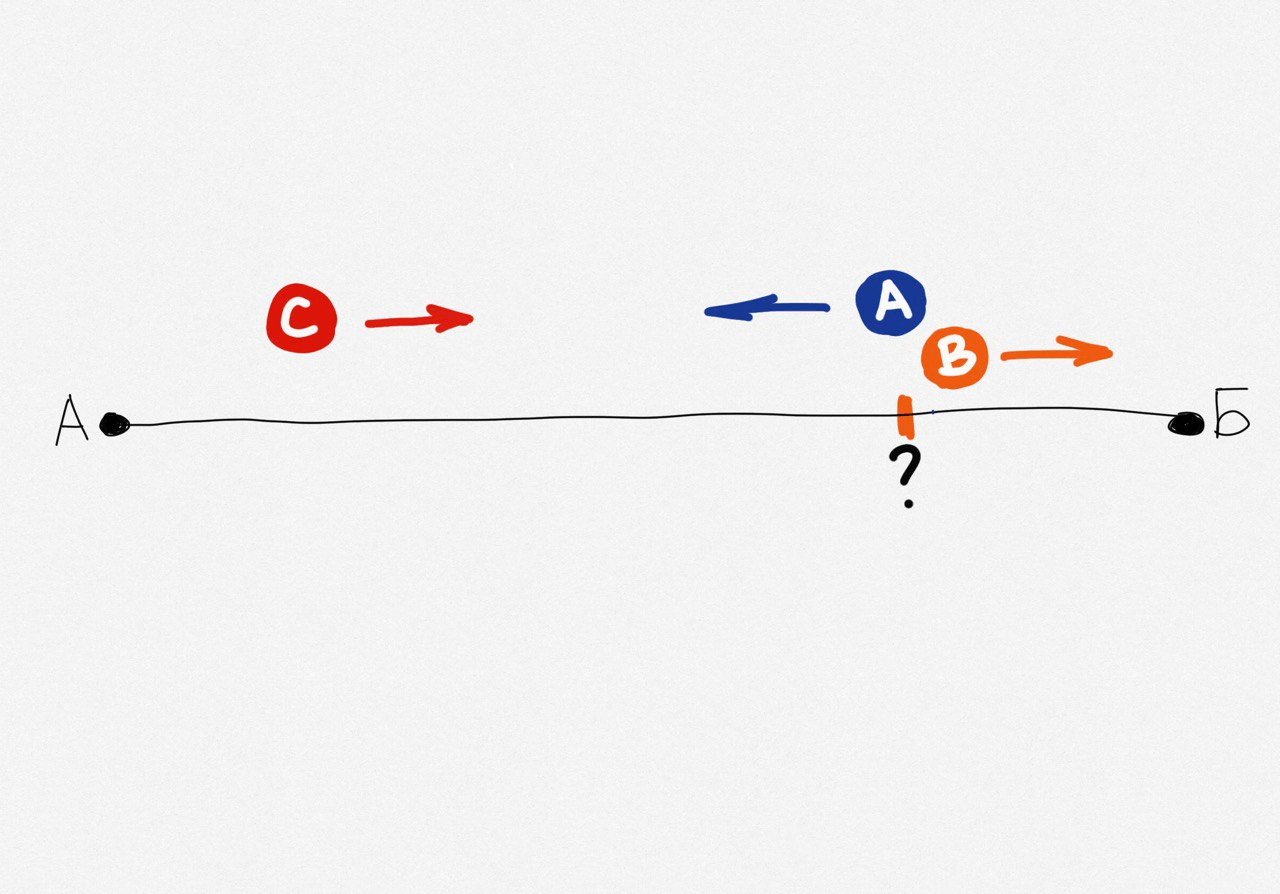
Теперь визуализируем весь план передвижений. Возьмём за А точку старта, за Б — точку финиша. В точке В1 Андрей оставит Вову. В это время Саша будет в точке С1. В точке С2 его подберёт Андрей, а Вова в этот момент достигнет точки В2:
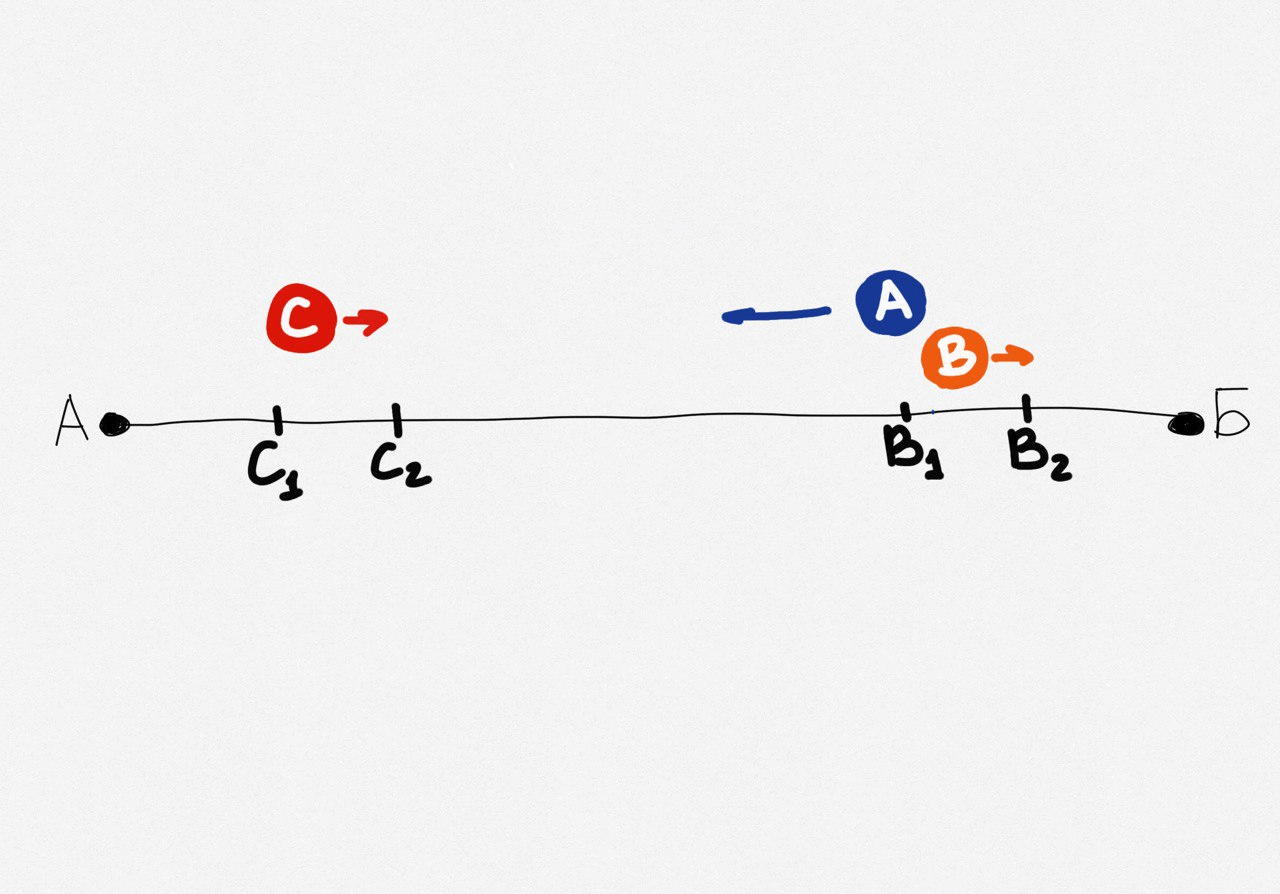
Теперь возьмём за t время, за которое Андрей вернётся на мопеде из точки В1 на точку С2, а расстояние от В1 до С2 возьмём за р:
t = В1С2/60 = р/60
За такое же время t Саша дойдёт из точки С1 до точки С2 (расстояние между ними возьмём за п):
t = С1С2/15 = п/15
За это же время t Вова дойдёт от точки В1 до В2:
t = В1В2/15
Так как в двух последних уравнениях у нас одинаковое время t и одинаковая скорость 15 км/ч, получается, что расстояние от С1 до С2 и от В1 до В2 — одинаковое:
t = п/15
Теперь на основании равенства времени t сравним расстояния р и п:
п/15 = р/60
р = 4п
Получаются такие отрезки:
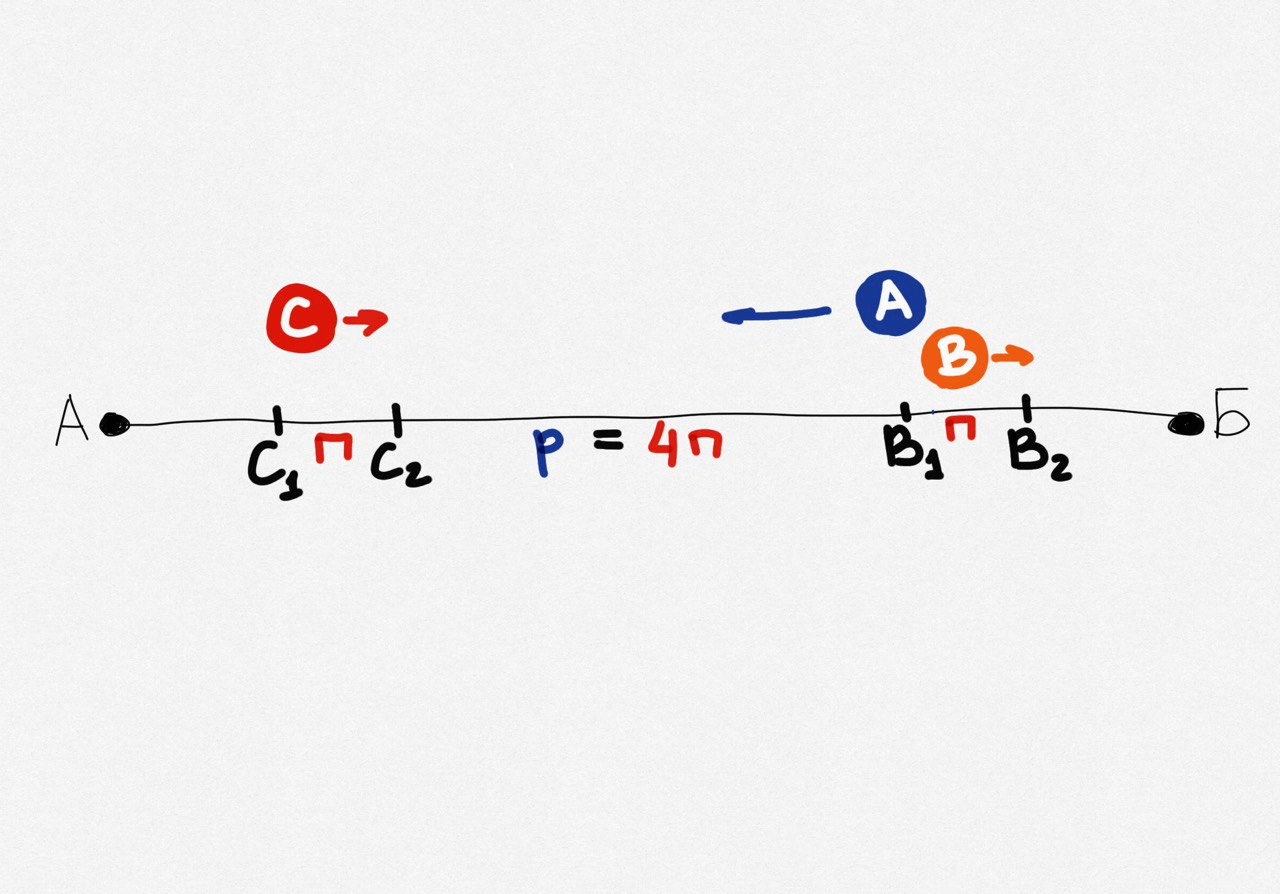
Теперь рассчитаем расстояние о, которое Вове останется пройти из точки В2 до Б. Время, за которое Андрей и Саша проедут расстояние 4п + п + о, будет равно времени, за которое Вова дойдёт расстояние о:
(4п + п + о)/60 = о/15
о = (5/3)п
Теперь наш план перемещений выглядит так:
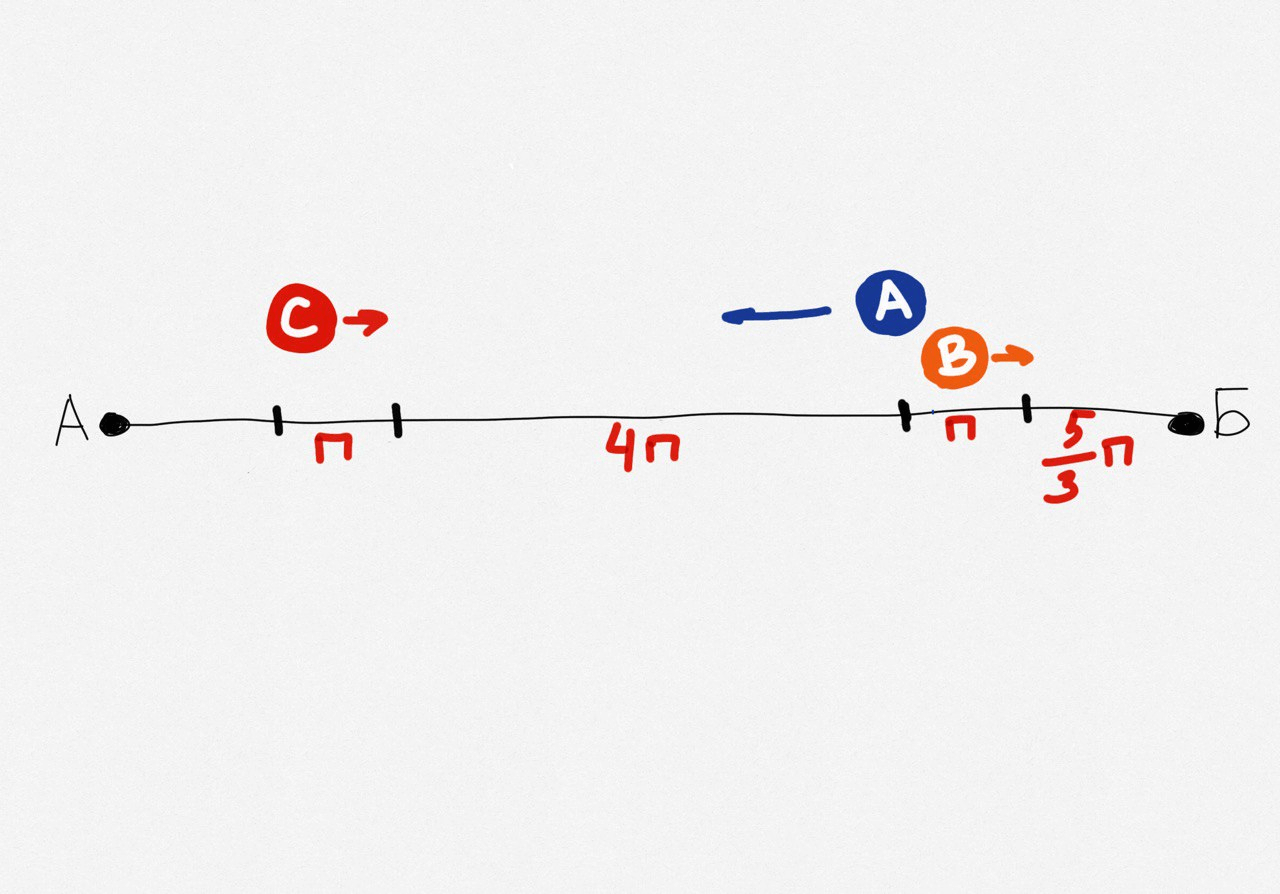
Нам осталось рассчитать расстояние н от точки старта А до С1. У нас снова получается равенство времени, за которое Саша дойдёт до точки C1, а Андрей с Вовой — доедут до точки В1:
н/15 = (н + п + 4п)/60
н = (5/3)п
Ещё раз визуализируем все пути:
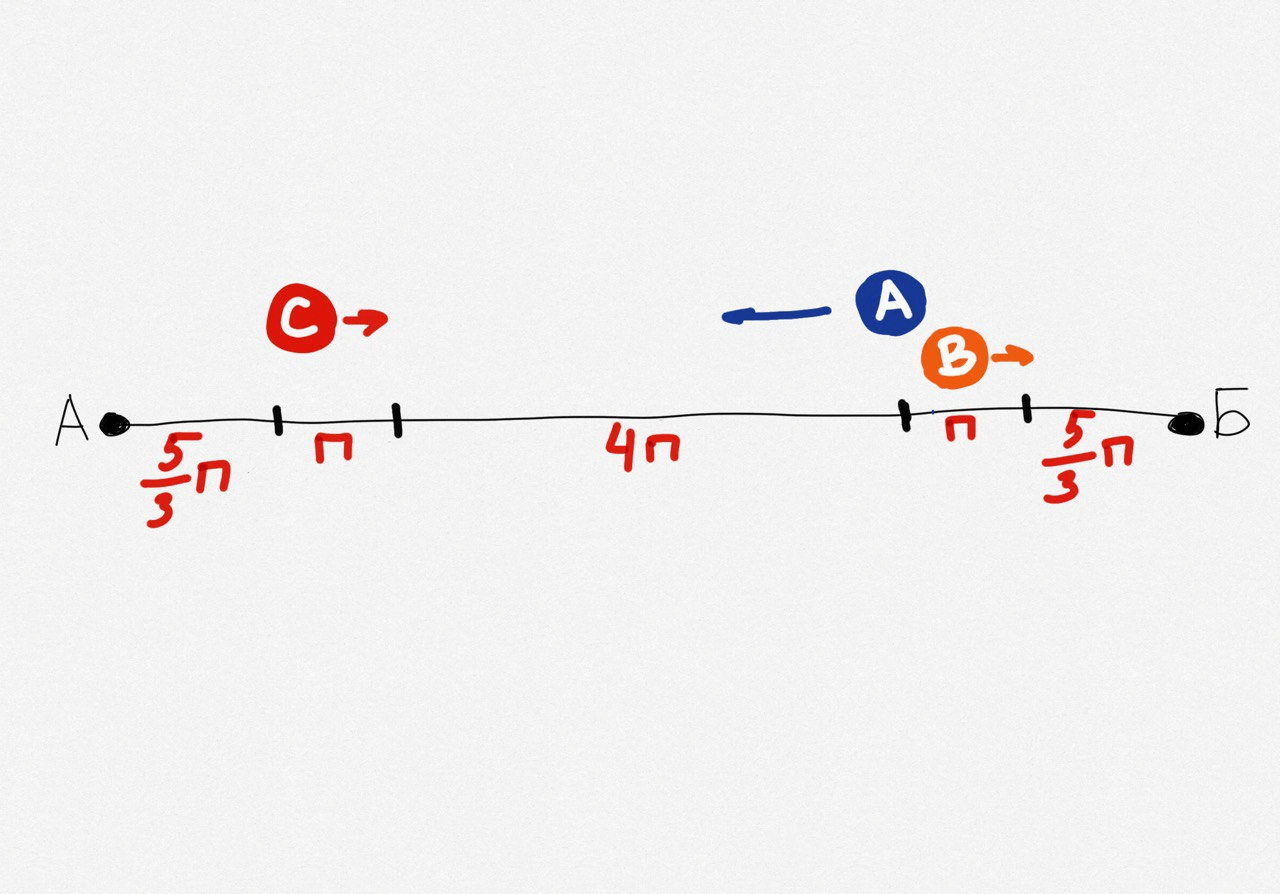
Получается такое равенство:
(5/3)п + п + 4п + п + (5/3)п = 300 км
п = 32,14 км
Подставим это значение в нашу визуализацию:
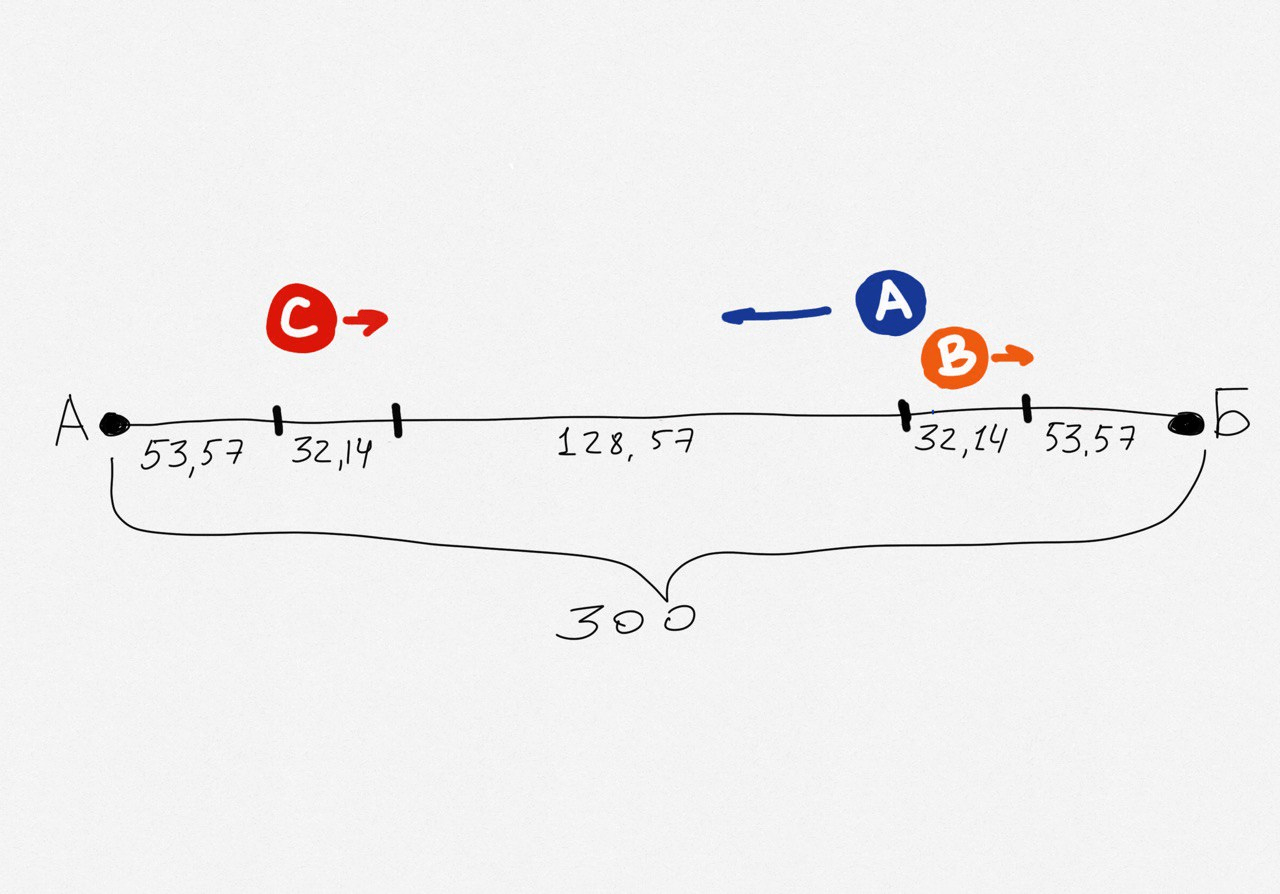
Теперь посчитаем самое короткое время, за которое все три айтишника доберутся из точки старта А до точки финиша Б. Посчитаем на примере Вовы:
t(Вова) = t(АВ1) + t(о)
t(Вова) = АВ1/60 + о/15
t(Вова) = 214,28/60 + 85,71/15
t(Вова) = 9,28 часа = 9 часов 17 минут
Получается, что самое короткое время составит примерно 9 часов, 17 минут.
Джуниоры и стартап
В один перспективный стартап одновременно взяли шесть джуниоров. Каждый месяц каждый из джуниоров может стать мидлом с вероятностью ½. Если повышение состоялось, оно уже не имеет обратной силы. Через сколько месяцев в среднем можно ожидать, что все шесть джуниоров станут мидлами?
Это задача про вероятности, поэтому вспомним основное:
Вероятность наступления какого-то события равна отношению количества нужных нам событий к общему количеству событий.
Например, вероятность выкинуть кубик с чётным числом очков считается так:
- Всего чётных граней на кубике — 3.
- Всего граней на кубике, которые могут выпасть при броске — 6.
- Вероятность выкинуть кубик с чётной гранью наверху будет равна 3 / 6 = ½
- Это значит, что с вероятностью 50% мы выкинем нужный нам результат при одном броске.
Теперь вернёмся к задаче.
Обозначим за Ах количество месяцев, которые должны пройти до того, как все джуны станут мидлами, где х — количество мидлов. В нашем случае у нас должно стать 6 мидлов, поэтому х = 6. Нам надо найти А0 — стартовую точку, которая покажет нам, сколько месяцев должно пройти, прежде чем все 6 станут мидлами.
Мы будем решать эту задачу в обратном порядке, поэтому следите за логикой.
Когда все джуны стали мидлами, это ситуация А6 — у нас 6 мидлов, а значит, 0 джунов. Получается, что А6 = 0, потому что все уже стали мидлами и не нужно ждать очередного месяца.
Теперь шагнём назад и посмотрим на ситуацию А5, когда у нас 5 мидлов и 1 джун. Вероятность того, что у нас через месяц джун станет мидлом — ½, либо станет, либо нет (и мы останемся в состоянии А5). Это значит, что количество месяцев, которое пройдёт, прежде чем этот джун станет мидлом равна:
А5 = 1 + ½ × А6 + ½ × А5, а единица здесь отвечает за месяц, который должен пройти, прежде чем любой джун станет мидлом.
Решим это уравнение. Мы выяснили, что А6 = 0, поэтому:
А5 = 1 + 0 + ½ × А5
А5 = 1 + ½ × А5 → А5 = 2
Откатимся ещё назад и посчитаем ожидаемое количество месяцев, до финала, когда у нас 4 мидла и 2 джуна — это А4. Сейчас распишем подробно решение, чтобы была понятна логика на следующих этапах.
У нас 2 джуна, каждый из которых может стать мидлом (а может и не стать). Получается, у нас 4 исхода месяца:
- Оба стали мидлами.
- Первый стал, а второй нет.
- Первый не стал, а второй стал.
- Оба не стали джунами (всё осталось как и было).
Зная это, получим формулу:
А4 = 1 (прошёл месяц) + ¼ × А6 (оба стали мидлами) + 2/4 × А5 (один стал, а другой нет) + ¼ × А4 (оба не стали)
А4 = 1 + ¼ × А6 + 2/4 × А5 + ¼ × А4 ← подставим сюда уже известные значения А6 и А5
А4 = 1 + 0 + ½ × 2 + ¼ × А4
А4 = 8/3
Откатимся снова и получим ситуацию, когда у нас 3 мидла и 3 джуна — это ситуация А3. Всего у нас может быть 8 исходов, когда кто-то становится мидлом, а кто-то нет (2³ = 8) и 4 возможных исхода:
- Все стали сразу мидлами — вероятность ⅛, и переходим в ситуацию А6.
- Двое из трёх стали мидлами — вероятность ⅜, и переходим в ситуацию А5.
- Один из трёх стал мидлом — вероятность ⅜, и переходим в ситуацию А4.
- Никто не стал мидлом — вероятность ⅛, и остаёмся в ситуации А3.
Запишем это в виде уже привычной формулы:
А3 = 1 + ⅛ × А6 + ⅜ × А5 + ⅜ × А4 + ⅛ × А3
Подставим уже известные значения А6, А5 и А4 и получим значение А3:
А3 = 22/7
Снова откатываемся назад и смотрим на ситуацию А2, когда у нас 2 мидла и 4 джуна. Теперь у нас 2⁴ = 16 возможных ситуаций и 5 разных исходов:
- Все стали мидлами — вероятность 1/16, и переходим в ситуацию А6
- Трое стали мидлами — вероятность 4/16, и переходим в ситуацию А5.
- Двое стали мидлами — вероятность 6/16, и переходим в ситуацию А4.
- Один стал мидлом — вероятность 4/16, и переходим в ситуацию А3.
- Никто не стал мидлом — вероятность 1/16, и остаёмся в ситуации А2.
Составим формулу для А2 и потом подставим уже известные значения А6 — А3:
А2 = 1 + 1/16 × А6 + 4/16 × А5 + 6/16 × А4 + 4/16 × А3 + 1/16 × А2
А2 = 368/105
Откатимся ещё на шаг назад и посмотрим на ситуацию А1, когда у нас 1 мидл и 5 джунов. Здесь 2⁵ = 32 возможных ситуаций и 6 возможных ситуаций:
- Все стали мидлами — вероятность 1/32 → А6.
- Четверо стали мидлами — вероятность 5/32 → А5.
- Трое стали мидлами — вероятность 10/32 → А4.
- Двое стали мидлами — вероятность 10/32 → А3.
- Один стал мидлом — вероятность 5/32 → А2.
- Никто не стал мидлом — вероятность 1/32, и остаёмся в ситуации А1.
Составим формулу для А1 и потом подставим уже известные значения А6—А2:
А1 = 1 + 1/32 × А6 + 5/32 × А5 + 10/32 × А4 + 10/32 × А3 + 5/32 × А2 + 1/32 × А1
А1 = 2470/651
И наконец, откатимся до стартового условия, когда у нас 0 мидлов и 6 джунов — то, что нам и нужно найти. Здесь 2⁶ = 64 возможных ситуации и 7 возможных исходов:
- Все стали мидлами → вероятность 1/64 → А6.
- Пятеро стали мидлами → вероятность 6/64 → А5.
- Четверо стали мидлами → вероятность 15/64 → А4.
- Трое стали мидлами → вероятность 20/64 → А3.
- Двое стали мидлами → вероятность151/64 → А2.
- Один стал мидлом → вероятность 6/64 → А1.
- Никто не стал мидлом → вероятность 1/64 → остаёмся в ситуации А0.
Составим формулу для А0 и потом подставим уже известные значения А6—А1:
А0 = 1 + 1/64 × А6 + 6/64 × А5 + 15/64 × А4 + 20/64 × А3 + 15/64 × А2 + 6/64 × А1 + 1/64 × А0
А0 = 7880/1953 ≈ 4,03
Получается, что ожидаемое время, когда все 6 джунов станут мидлами — 4,03 месяца. Но так как повышение происходит каждый месяц, нужно округлить до 5. Но это не значит, что через 5 месяцев все ТОЧНО станут мидлами — это лишь среднее значение вероятности, что скорее всего это произойдёт через это время.
Уф. Решили. Вы — крутые, если дочитали досюда.
День рождения двух программистов
Однажды джун и мидл поспорили о том, кто из них лучше мыслит логически. Чтобы разрешить свой спор, они позвали сеньора. Сеньор придумал для них такую задачку: «Вы оба знаете, в какой день недели вы родились, но не знаете, в какой день родился другой. Я задам вам этот вопрос по очереди. Победит тот, кто первым угадает день рождения другого».
Затем сеньор дал две подсказки: джун родился не в понедельник, а вообще дни рождения джуна и мидла идут рядом — как предыдущий или следующий. После этого сеньор спросил по очереди мидла и джуна, догадался ли каждый о дне рождения соперника. Их ответы были такими:
Мидл: Нет.
Джун: Нет.
Мидл: Нет.
Джун: Нет.
Мидл: Нет.
Джун: Да!
А вы сможете вычислить, в какой день недели родился мидл?
У нас есть 14 вариантов пар:
| Мидл | Джун | Мидл | Джун | |
| воскресенье | понедельник | среда | вторник | |
| воскресенье | суббота | четверг | пятница | |
| понедельник | воскресенье | четверг | среда | |
| понедельник | вторник | пятница | суббота | |
| вторник | среда | пятница | четверг | |
| вторник | понедельник | суббота | воскресенье | |
| среда | четверг | суббота | пятница |
Поскольку мы знаем, что джун родился не в понедельник, мы можем сразу отбросить два варианта: «воскресенье, понедельник» и «вторник, понедельник»:
| Мидл | Джун | Мидл | Джун | |
| среда | вторник | |||
| воскресенье | суббота | четверг | пятница | |
| понедельник | воскресенье | четверг | среда | |
| понедельник | вторник | пятница | суббота | |
| вторник | среда | пятница | четверг | |
| суббота | воскресенье | |||
| среда | четверг | суббота | пятница |
Если бы мидл родился в воскресенье или вторник, у него были бы соответственно однозначные варианты ответа: суббота или среда (потому что джун точно не родился в понедельник). Но мидл пока не догадался, в какой день недели родился джун (ответил «нет» в первый раз). Отбрасываем варианты «воскресенье, суббота» и «вторник, среда»:
| Мидл | Джун | Мидл | Джун | |
| среда | вторник | |||
| четверг | пятница | |||
| понедельник | воскресенье | четверг | среда | |
| понедельник | вторник | пятница | суббота | |
| пятница | четверг | |||
| суббота | воскресенье | |||
| среда | четверг | суббота | пятница |
По ответам мидла джун понимает, что мидл не родился в воскресенье и вторник. И если бы джун родился в субботу, у него был бы однозначный ответ, что мидл родился в пятницу. А если бы джун родился в среду, то он сказал бы, что мидл родился в четверг. Но джун тоже пока не догадался (ответил «нет» в первый раз). Можно отбросить варианты «пятница, суббота» и «четверг, среда»:
| Мидл | Джун | Мидл | Джун | |
| среда | вторник | |||
| четверг | пятница | |||
| понедельник | воскресенье | |||
| понедельник | вторник | |||
| пятница | четверг | |||
| суббота | воскресенье | |||
| среда | четверг | суббота | пятница |
Если бы мидл родился в четверг или пятницу, у него был бы однозначный вариант, что джун родился в пятницу или четверг (поскольку мы отмели вариант, что он родился в среду и субботу). Но раз мидл пока не догадался (ответил «нет» во второй раз), отбрасываем варианты «четверг, пятница» и «пятница, четверг»:
| Мидл | Джун | Мидл | Джун | |
| среда | вторник | |||
| понедельник | воскресенье | |||
| понедельник | вторник | |||
| суббота | воскресенье | |||
| среда | четверг | суббота | пятница |
Если бы джун родился в пятницу или четверг, у него был бы однозначный вариант, что мидл родился в субботу или среду (поскольку мы отмели вариант, что он родился в четверг). Но раз джун пока не догадался (ответил «нет» во второй раз), мы можем отбросить варианты «суббота, пятница» и «среда, четверг»:
| Мидл | Джун | Мидл | Джун | |
| среда | вторник | |||
| понедельник | воскресенье | |||
| понедельник | вторник | |||
| суббота | воскресенье | |||
Если бы мидл родился в среду или субботу, у него был бы однозначный ответ, что джун родился во вторник или воскресенье (поскольку он точно не родился в четверг или пятницу). Но мидл всё ещё не угадал день рождения джуна (ответил «нет» в третий раз). Значит, варианты «суббота, пятница» неправильный:
| Мидл | Джун | Мидл | Джун | |
| понедельник | воскресенье | |||
| понедельник | вторник | |||
Таким образом, у нас остался только один вариант: мидл родился в понедельник. Поэтому джун победил.
Задача со звёздочкой: тренер и каратист
Один каратист-программист после своего дня рождения заметил, что его возраст сейчас равен сумме цифр в возрасте его тренера. А через 5 лет возраст каратиста-программиста станет равен произведению цифр, из которых состоит возраст тренера.
Но сколько тогда лет каратисту сейчас?
На всякий случай скажем, что возраст тренера состоит из двух цифр.
У этой задачи есть два варианта решения: как её решил бы математик и как программист. Мы сэкономим время и сразу пойдём простым путём — заставим машину поработать за нас и просто посмотрим на правильный ответ. Для этого нам понадобятся гуглотаблицы или Эксель, чтобы они сами посчитали все данные.
Чтобы ничего не устанавливать дополнительно на компьютер, создадим новую таблицу по ссылке:
https://docs.google.com/spreadsheets/create
Теперь сделаем 2 колонки — возраст тренера и программиста. Так как возраст тренера состоит из двух цифр, то минимальное двузначное число это 10, а максимальное — 99. Начнём с минимального:
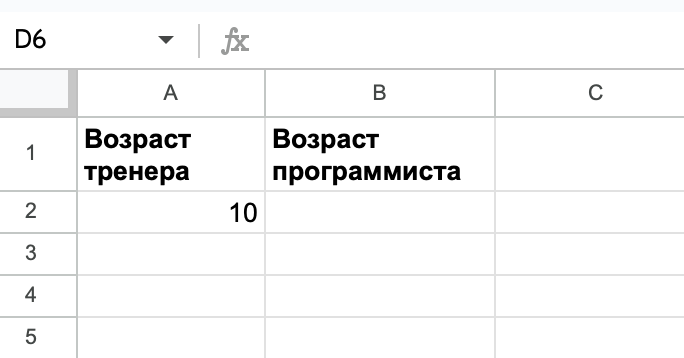
Мы не будем заполнять колонку с возрастом программиста вручную. Вместо этого мы напишем там формулу, которая сама возьмёт цифры из возраста тренера и сложит их друг с другом:
= left(A2;1) + right(A2;1)
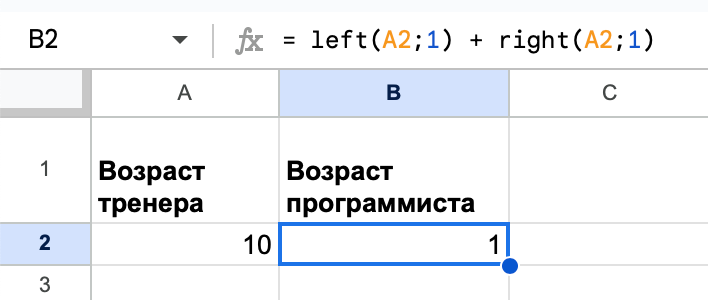
Теперь добавим ещё пару колонок с возрастом, который будет у обоих через 5 лет. С тренером сделаем просто — возьмём возраст из первой колонки и прибавим к нему 5:
= A2 + 5

А у программиста через 5 лет возраст будет равен произведению цифр возраста тренера. Используем те же команды, что и в первом случае, только будем теперь не складывать цифры, а перемножать их, чтобы получить возраст программиста:
= left(D2;1) * right(D2;1)

Но у нас уже есть исходный возраст программиста из второй колонки, поэтому мы тоже можем прибавить к нему 5 и посмотреть, сколько на самом деле ему будет лет:

Последнее, что нам осталось сделать на этом этапе, — сравнить реальный возраст программиста через 5 лет и тот, который получился перемножением цифр возраста тренера. Для этого добавим простую проверку условия: если последние две колонки равны, то выводим 1, иначе — 0.
Создаём новую колонку и пишем такую формулу:
= if(E2 = F2; 1; 0)

Так мы проверили только один возраст, когда тренеру 10 лет. Но нам нужно проверить всё от 10 до 99 лет — для этого мы напишем под возрастом тренера в новую ячейку число 11, потом выделим эти две ячейки и протянем их вниз, до 99:
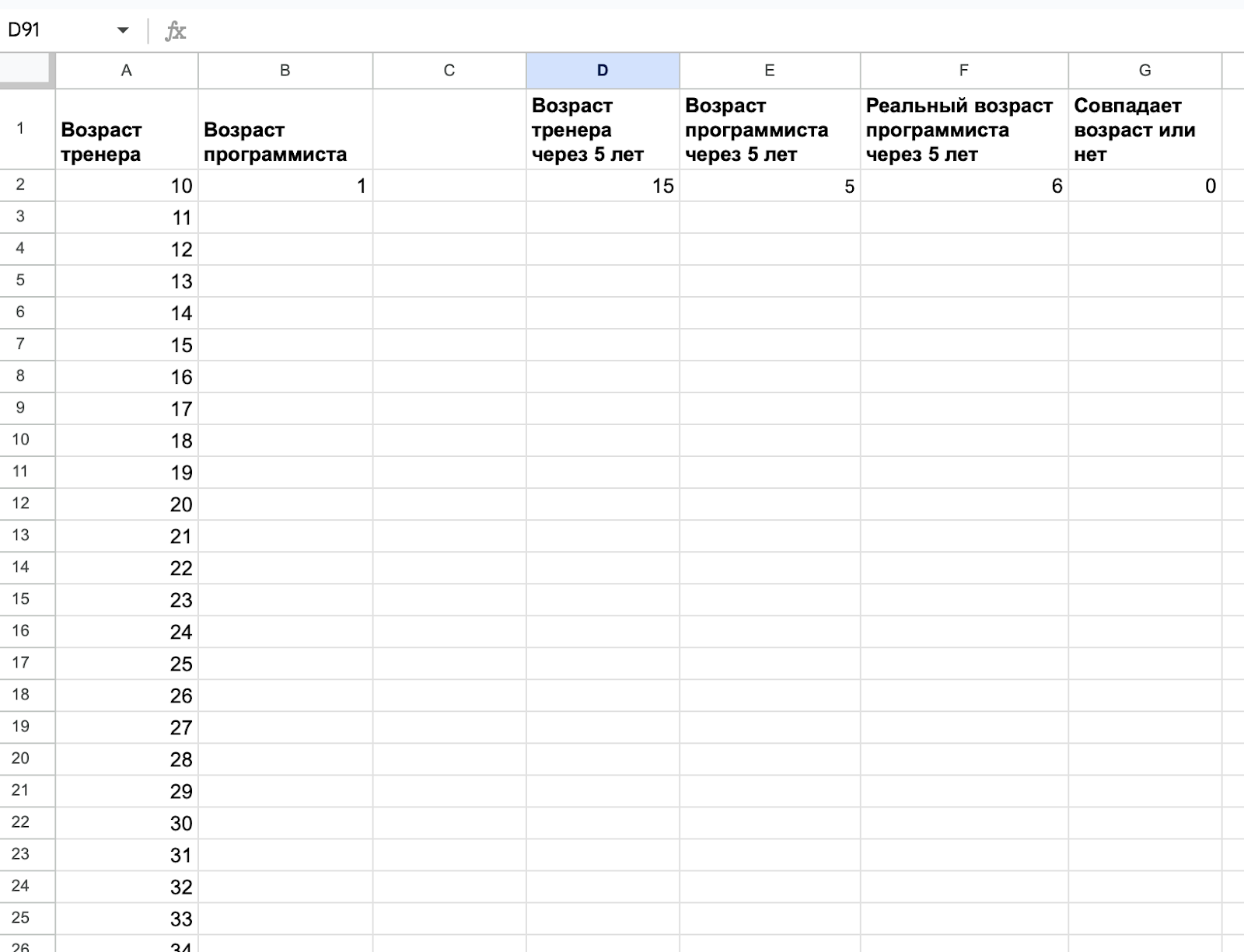
Теперь сделаем то же самое с остальными ячейками: выделим всю оставшуюся строку, начиная со второй колонки, и протянем её вниз до девяносто первой ячейки.
Выделяем…
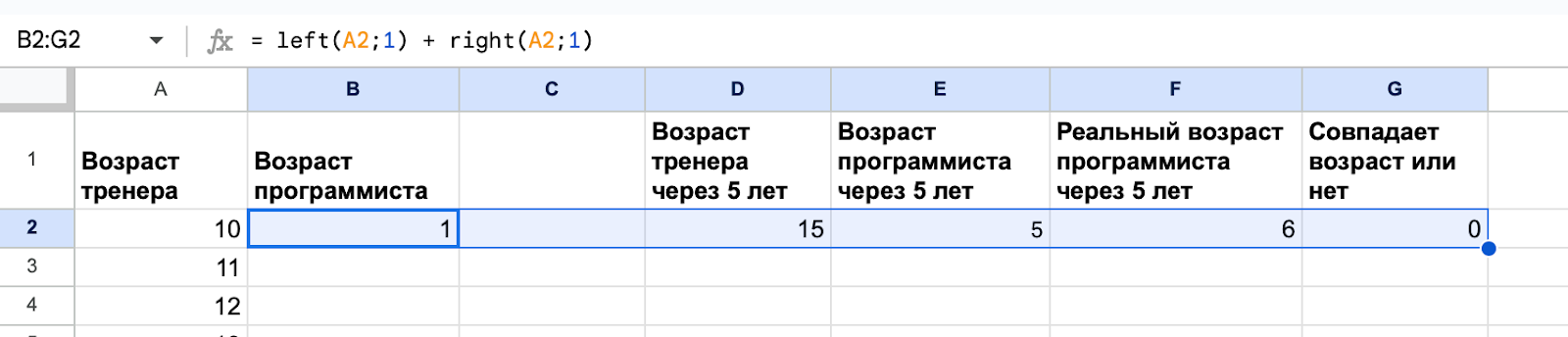
… и протягиваем вниз:
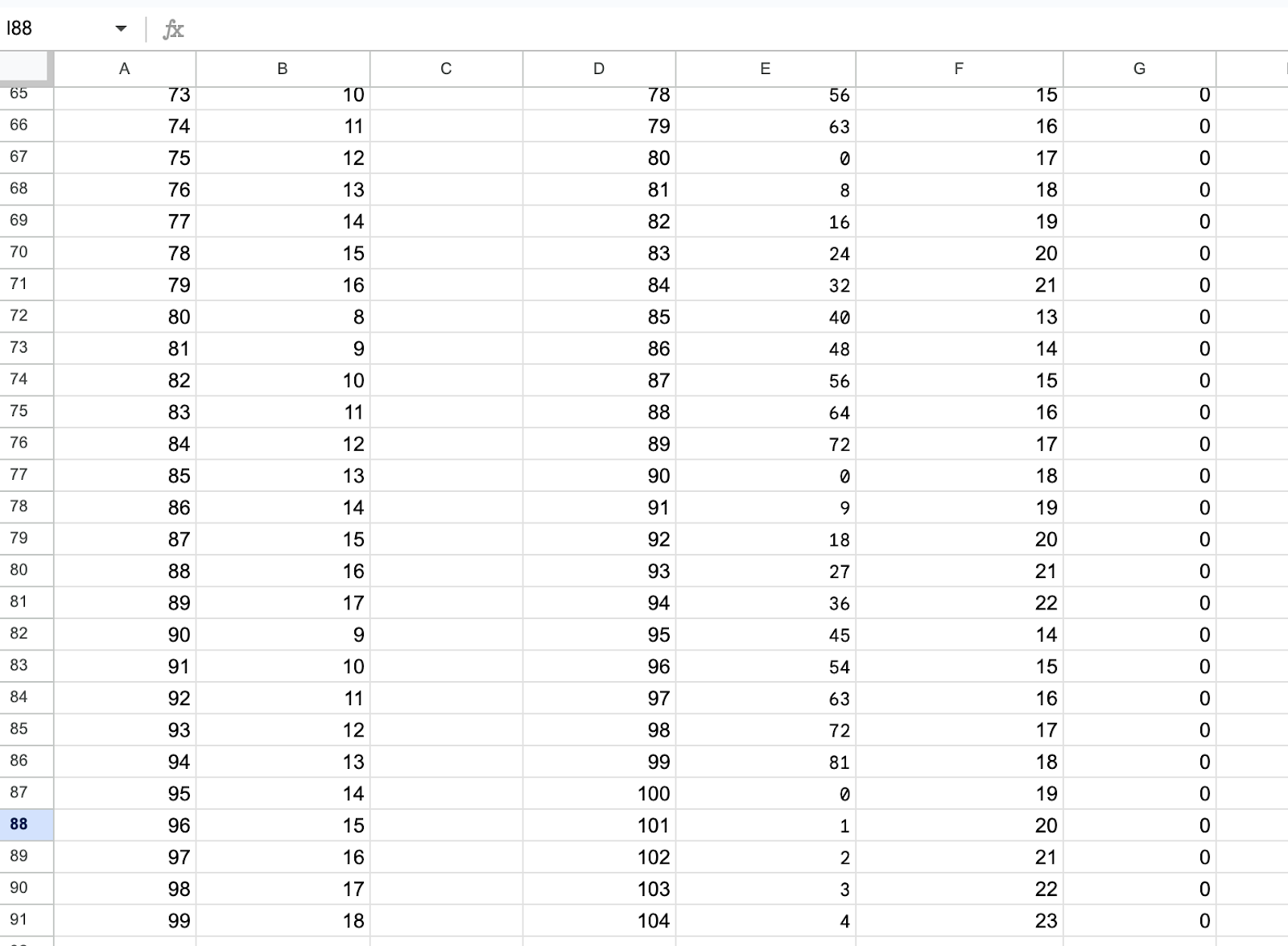
И теперь нам осталось только посмотреть на последнюю колонку и найти там единицу — признак того, что реальный возраст каратиста совпадёт с расчётным через 5 лет. Такая строка в таблице всего одна:
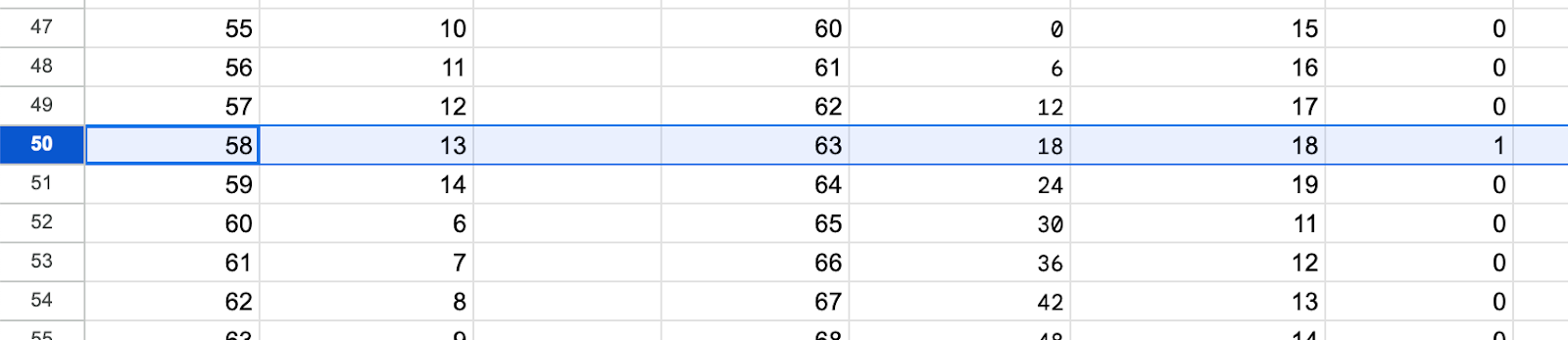
Получается, что сейчас тренеру 58 лет, а каратисту-программисту — 13. Давайте это сравним с тем, что написано в условиях:
58 → 5 + 8 = 13 — совпадает с возрастом каратиста.
Через 5 лет тренеру будет 63, а каратисту — 18, что совпадает с нашими расчётами:
63 → 6 × 3 = 18 ← 13 + 5
Вот так знание основ программирования и табличных редакторов помогает решить сложную задачу за 5 минут.