Сегодня вы получите рабочий алгоритм решения сложных задач в теории игр. От теории к реально применимой практике.
Когда мы разбирали теорию игр, то выяснили такое:
- Теория игр — это набор инструментов, которые помогают принимать взвешенные, рациональные и точные решения, а также понимать данные.
- В игре, которую мы анализируем, должно быть не меньше двух участников. У каждого должен быть свой интерес и несколько вариантов действия.
- Каждый принимает решения на основании информации о действиях других.
- Есть какие-то общие правила, которые известны всем.
С этой точки зрения большинство наших бытовых ситуаций попадает под действие теории игр. Даже обычные переговоры о зарплате или о том, где провести отпуск, — в них тоже действует теория игр.
Так вот: существует алгоритм, который позволяет принимать максимально правильные решения даже в очень сложных ситуациях. Он называется правилом минимакс.
Стратегия
В теории игр задача каждого игрока — найти стратегию, которая принесёт ему больше всего пользы.
В теории игр есть такое деление: игры с нулевой и ненулевой суммой. Игра с нулевой суммой означает, что если выиграл один, то все остальные проиграли. Большинство классических игр и много жизненных ситуаций — как раз игры с нулевой суммой. Это значит, что каждый игрок будет стремиться к тому, чтобы улучшить своё положение и тем самым ухудшить положение других игроков.
Если игрок понимает, что действия других могут ухудшить его положение, ему нужна стратегия, которая позволит снизить это влияние и как минимум закончить игру с минимальными потерями. Для этого применяется правило минимакс.
Правило минимакса
Чтобы понять, как работает правило минимакса, следите за логикой игрока:
- В одних играх есть степень поражения — например, сколько денег потерял игрок в конце игры. В других степень поражения определяется самим фактом проигрыша, без уточнения деталей, просто — выиграл или проиграл.
- Каждый другой игрок принимает решения, которые могут увеличить ваш максимально возможный проигрыш. Например, после его ходов вы можете потерять 10 или 500 очков. Максимально возможный проигрыш здесь — 500 очков.
- Наша задача — на каждом шаге принимать такие решения, чтобы минимизировать этот проигрыш. Проще говоря, сделать так, что, даже если бы мы и потеряли очки на этом ходу, то не 500, а 10 — минимальное количество из возможных.
Правило минимакс как раз и означает, что мы стремимся минимизировать максимально возможный проигрыш. Признак минимаксной стратегии звучит так:
Это лучшая минимаксная стратегия, потому что в ней даже самый плохой вариант гораздо лучше всех остальных плохих вариантов при других стратегиях.
Как работает алгоритм минимакса
Разберём работу алгоритма минимакса на примере игры в крестики-нолики. Чтобы выиграть, нужно собрать ряд по горизонтали, вертикали или диагонали. Зная это, составим такой алгоритм, когда мы играем за второго игрока:
- Первый игрок ставит крестик в любом месте поля. Всего клеток 9, одну он занял, осталось 8.
- Мы по очереди виртуально ставим нолики в оставшиеся 8 клеток и оцениваем ситуацию, выиграли ли мы или проиграли. Если непонятно — закидываем уже новую ситуацию в алгоритм и прогоняем её с новыми вводными.
- Так делаем до тех пор, пока не заполнятся все клетки — при этом у нас будет очень много вариантов и ветвлений.
- С теми ветками, где мы выиграли, каждому своему ходу в определённую клетку добавляем какое-то количество очков, а где проиграли — отнимаем такое же количество.
- После просчёта мы получим для каждой из 8 клеток, с которых начали в самом начале, свою оценку хода.
- Наконец, мы выбираем для ответного хода ту клетку, которая набрала больше всего очков, и ставим нолик туда.
Получается, что мы рекурсивно просчитываем все ходы (или на определённую глубину вложенности, если ресурсов не хватает) и оцениваем результативность каждой клетки. Клетка, которая сработает лучше всего в большинстве стратегий и ходов, и будет клеткой, куда нам нужно поставить нолик.
Если вам вдруг нужна аналогия из фильма Марвел «Война бесконечности»:
Доктор Стрэндж: Я ускорил время… Посмотрел варианты будущего, чтобы оценить все вероятные исходы конфликта.
Старлорд: И много увидел?
Доктор Стрэндж: 14 000 625.
Тони Старк: Сколько победных?
Доктор Стрэндж: Один.
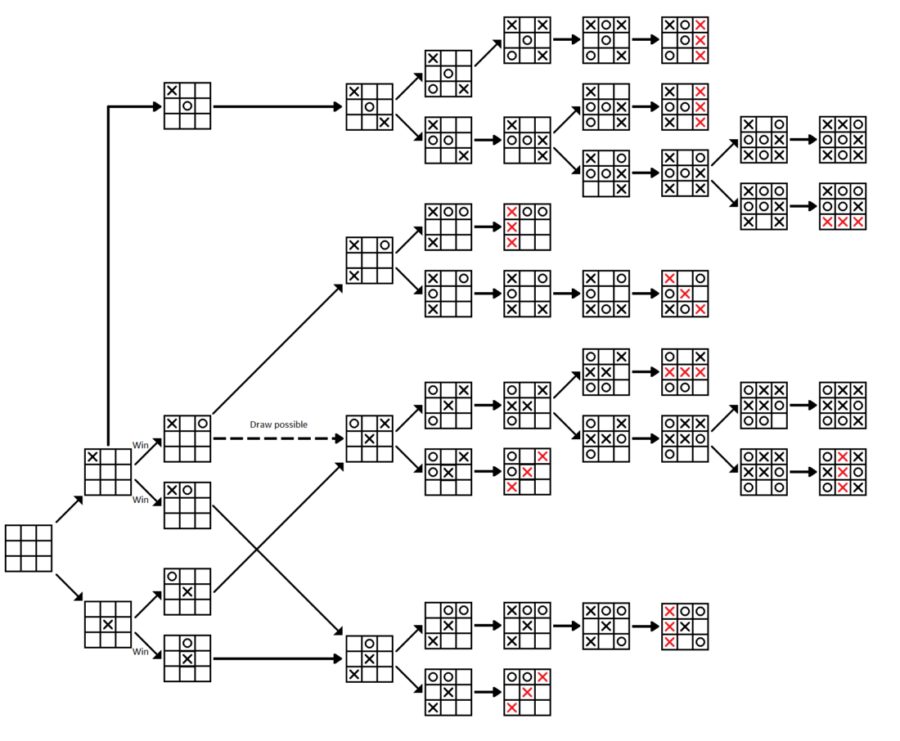
Как правило минимакса работает в жизни
Допустим, на улице в небольшом городе расположены сразу три продуктовых магазина, у которых разные владельцы. Задача каждого — получить максимум прибыли. Для этого нужно, чтобы покупки делали именно в этом магазине. Очевидное решение — немного снизить цену на базовые продукты, чтобы привлечь покупателей. Они придут за дешёвым хлебом и молоком и по пути здесь же возьмут всё остальное.
Но продавец понимает, что после этого владельцы других магазинов могут сделать то же самое или что-то другое: придумать акции или снизить цены на другие продукты. Это значит, что ему придётся делать ответный ход, чтобы удержать лидерство и приводить к себе большинство покупателей. И в ответ на этот ход конкуренты тоже сделают что-то своё.
Если у продавца есть статистика продаж, нужные цифры и показатели, он может просчитать несколько вариантов развития ситуации с некоторой глубиной, например в 2–4 хода с конкурентами. После этого он посмотрит на решения, которые встречаются чаще всего, и выберет из них те, что дают наибольший результат — это и будет оптимальным шагом в борьбе за количество покупателей.
👉 Описанная стратегия, кстати, называется максиминным алгоритмом (слова идут в обратном порядке). Это значит, что в ней нужно максимизировать минимально возможный выигрыш.
Где оно применяется в ИТ
Минимаксный алгоритм применяется почти в любых играх, когда нужно научить компьютер принимать выгодные для себя решения в зависимости от непредсказуемых действий игрока. При этом игры могут быть как обычными, например шашки или простые аркады, так и прикладными: как заключить наилучшую сделку, какую модель поведения выбрать, чтобы пройти отборочный тур, или как быть, когда невозможно что-то спрогнозировать до конца.
Что дальше
В следующей части мы проверим правило минимакса в деле — напишем игру в крестики-нолики и научим компьютер выбирать лучший ход. Подпишитесь, чтобы не пропустить продолжение.