А вот задачка на структуры данных, сортировку и алгоритмику, которая возможна только в нашей стране.
В Петербурге на улице Рубинштейна есть один бар, в который ходят лишь необщительные люди, назовём их интровертами. (На самом деле интроверты общительные, необщительность — это миф. Но это задачка, поэтому упростим.)
Интроверты садятся вдоль барной стойки, где есть 25 мест. Когда входит новый посетитель, он всегда садится у стойки как можно дальше от остальных гостей. Никто не садится на соседнее место рядом с другим интровертом: если кто-то входит и видит, что свободных мест мало, и надо сесть рядом с кем-то, то он уходит.
Бармен хочет получить как можно больше клиентов. У него есть право посадить самого первого посетителя на любое место у стойки. Куда выгоднее посадить первого интроверта с точки зрения бармена?
Для начала найдём идеальный вариант, который устроил бы бармена. Для этого нарисуем 25 квадратов в ряд и закрасим те, на которых кто-то сидит. Помните, что ни один интроверт по задаче не сядет на соседнее место к другому.
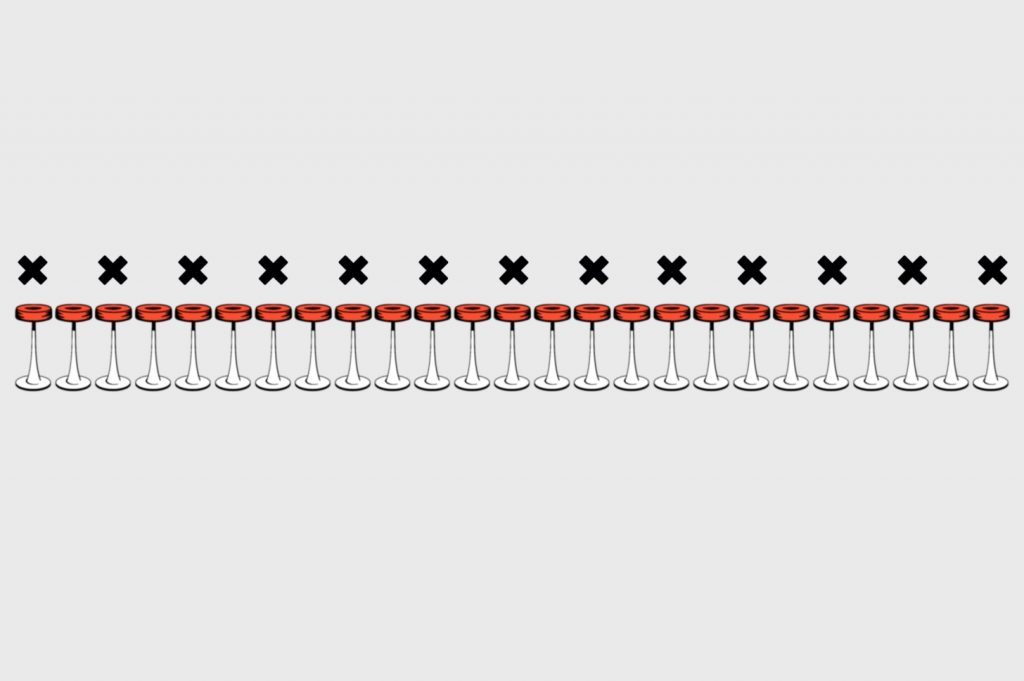
Получается, что это самая плотная рассадка, которая возможна в этом баре. Так у стойки сидят 13 человек. Осталось только найти место для самого первого посетителя.
Для начала попробуем решить эту задачу в лоб и посадим первого посетителя на первый стул:
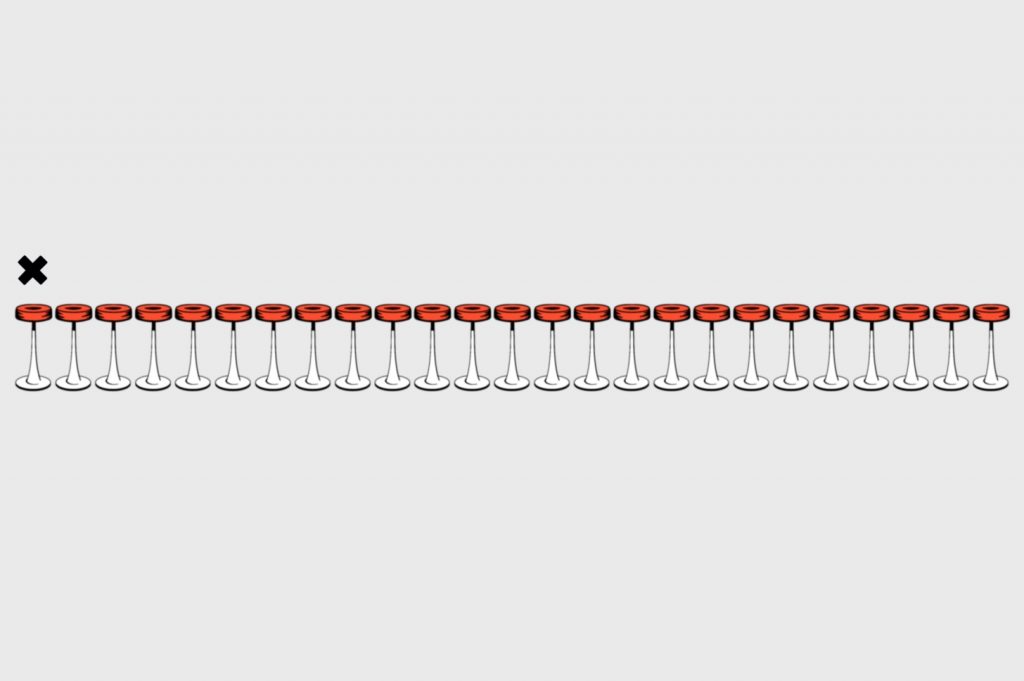
Теперь второй посетитель должен сесть на свободное место как можно дальше от него, то есть занять стул № 25:
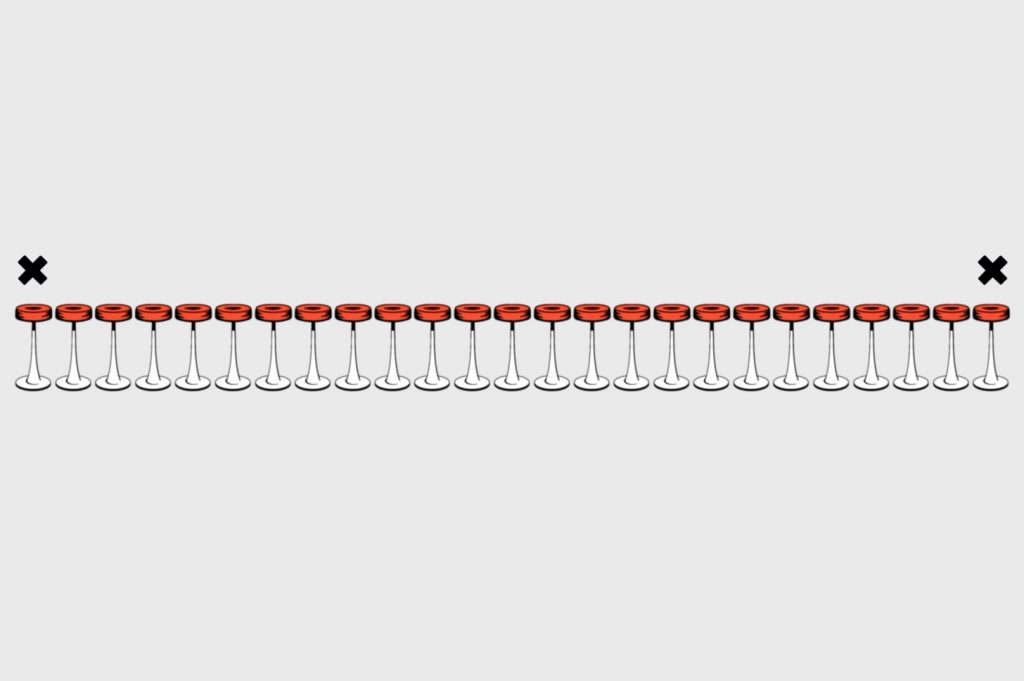
Третьему достаётся стул № 13, так как он ровно посередине между этими двумя:
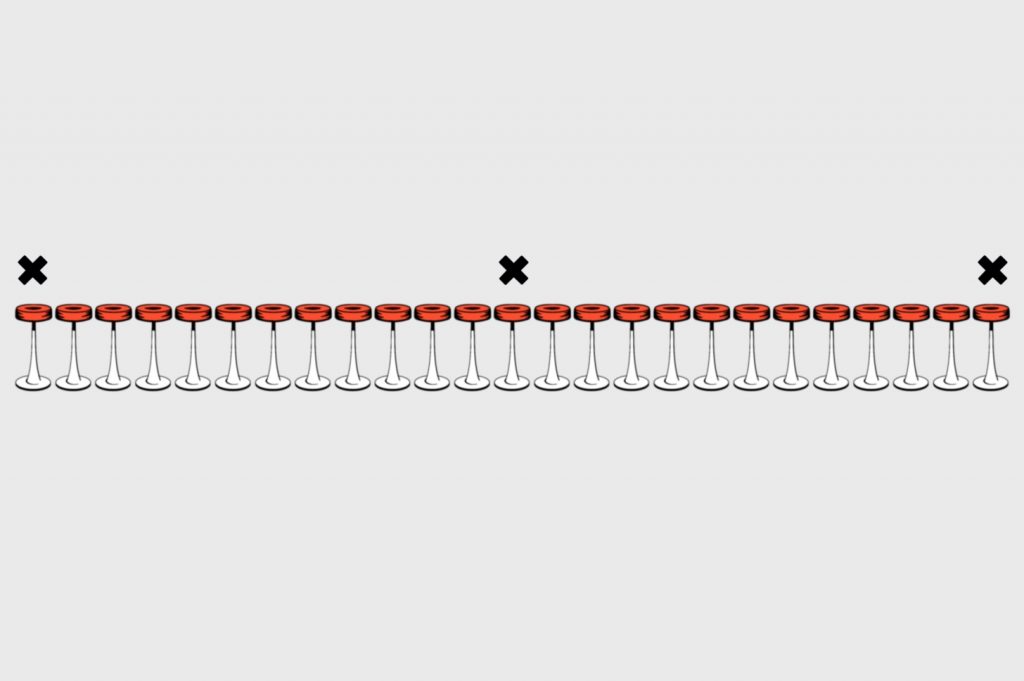
Два следующих займут свободные места точно посередине между центральным и боковыми:
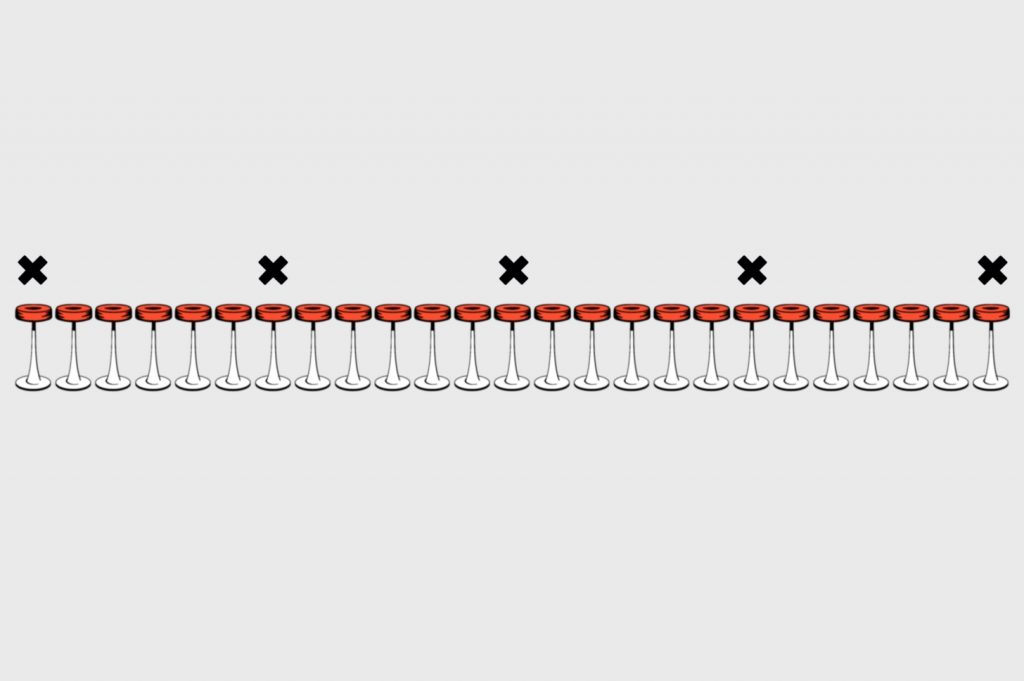
И вот тут настаёт момент истины: четыре следующих посетителя тоже сядут точно посередине между занятыми местами. Это значит, что между каждым будет по 2 пустых места:
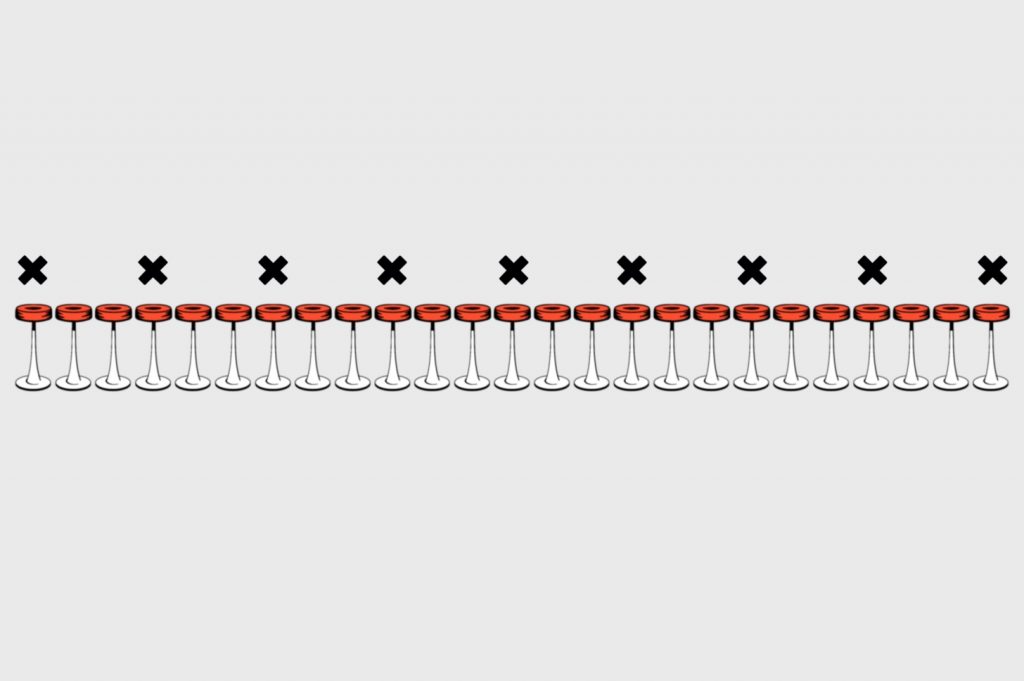
В итоге у нас занято всего 9 мест, но сесть больше никуда нельзя: у каждого свободного стула есть как минимум один занятый сосед. Значит, этот вариант не подходит. Нужен другой.
Чтобы прийти к правильному ответу, попробуем решать задачу с конца.
Вспомним идеальную рассадку:
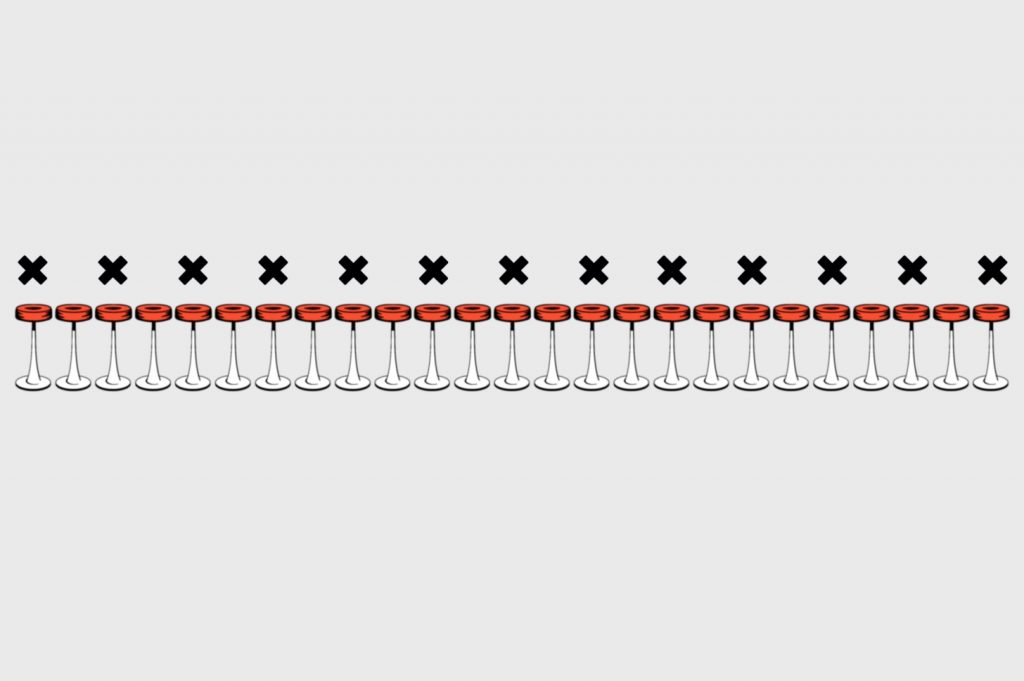
Здесь сидит максимальное количество гостей — 13, и между каждым из них есть свободное место. Отмотаем на шаг назад и посмотрим, как могли бы сидеть интроверты, чтобы новые гости сели точно между ними:
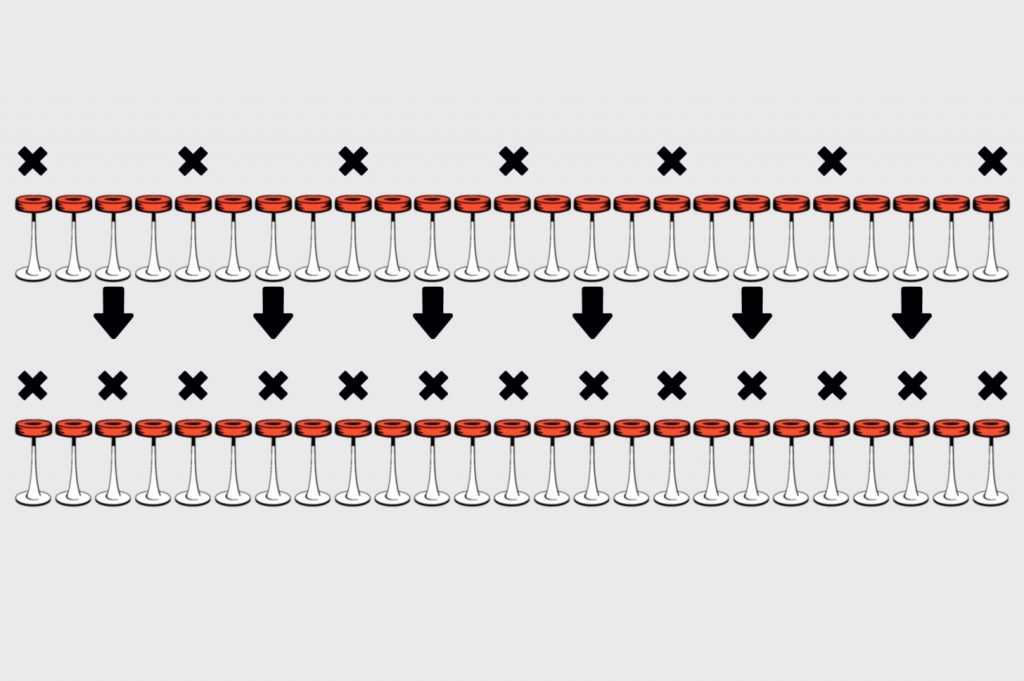
В этом случае 6 новых гостей садятся точно посередине между занятыми стульями и идеально заполняют все места.
Теперь сделаем ещё шаг назад и посмотрим, как должны сидеть гости, чтобы новые клиенты сели на нужные стулья:
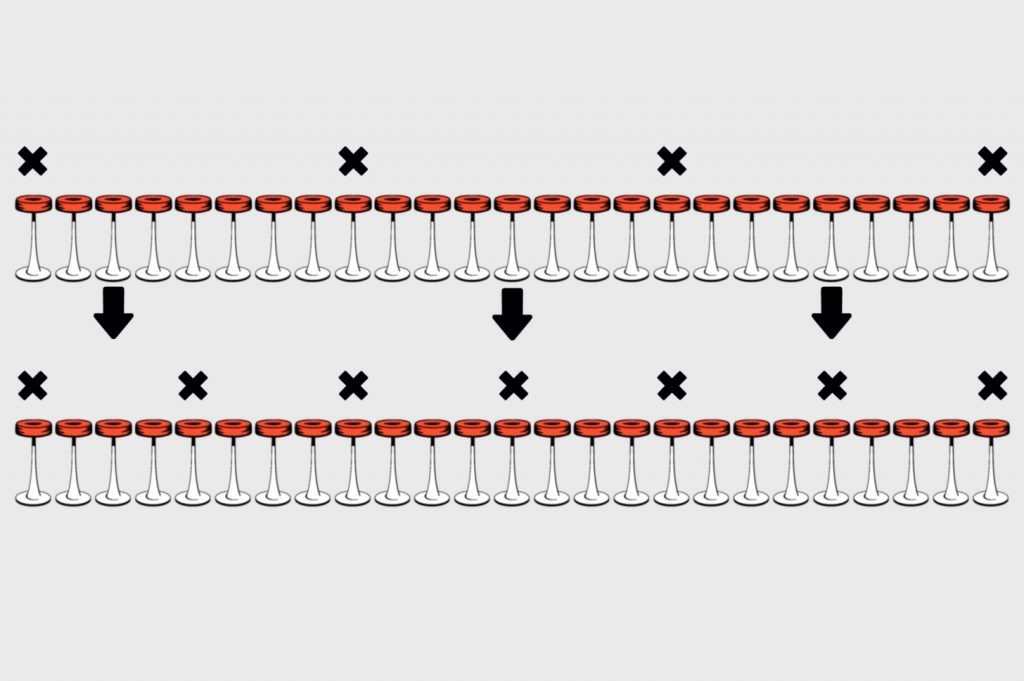
Получается, что если мы посадим первых четырёх гостей так, как на рисунке выше, то дальше всё будет хорошо. Сделаем ещё шаг назад, чтобы понять, как они смогли так сесть:
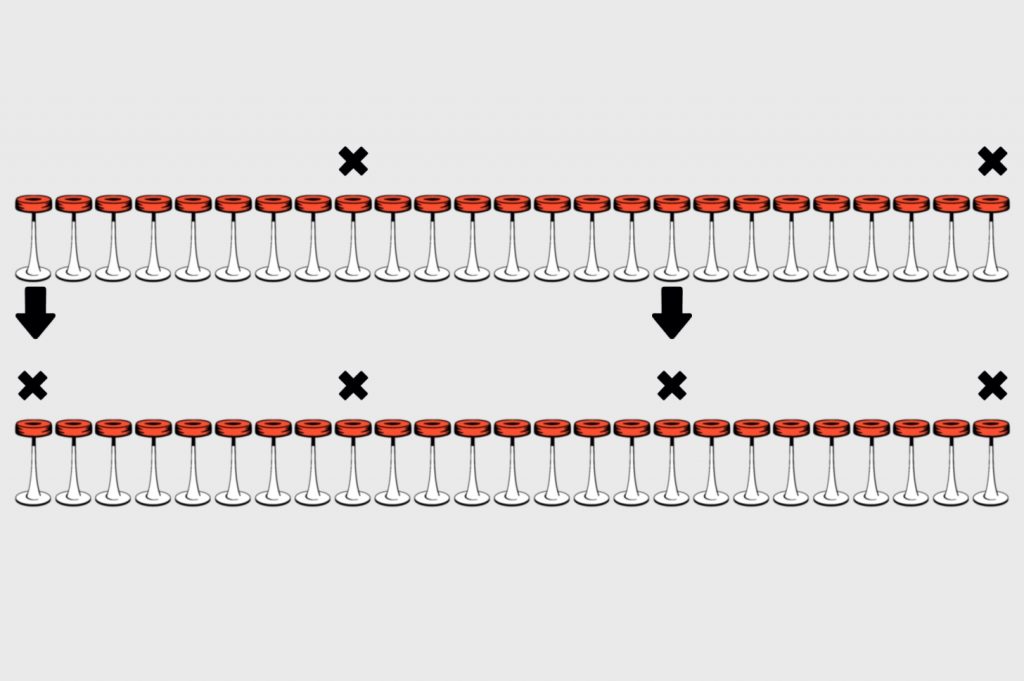
Из рисунка видно, что два новых посетителя должны сесть как можно дальше от занятых мест. Для этого один садится ровно посередине между двумя занятыми, а второй — с самого края, на первое место. Таким образом, между всеми ними будет максимально возможное расстояние. Осталось понять, как сели эти первые два интроверта.
Если бы первый гость сел с краю на стул № 25, второму бы пришлось сесть с противоположного края на стул № 1 (мы это разобрали в самом начале, в неправильном варианте). Значит, первый гость сел на стул № 9, а второму пришлось сесть максимально далеко от него — на самый последний стул:
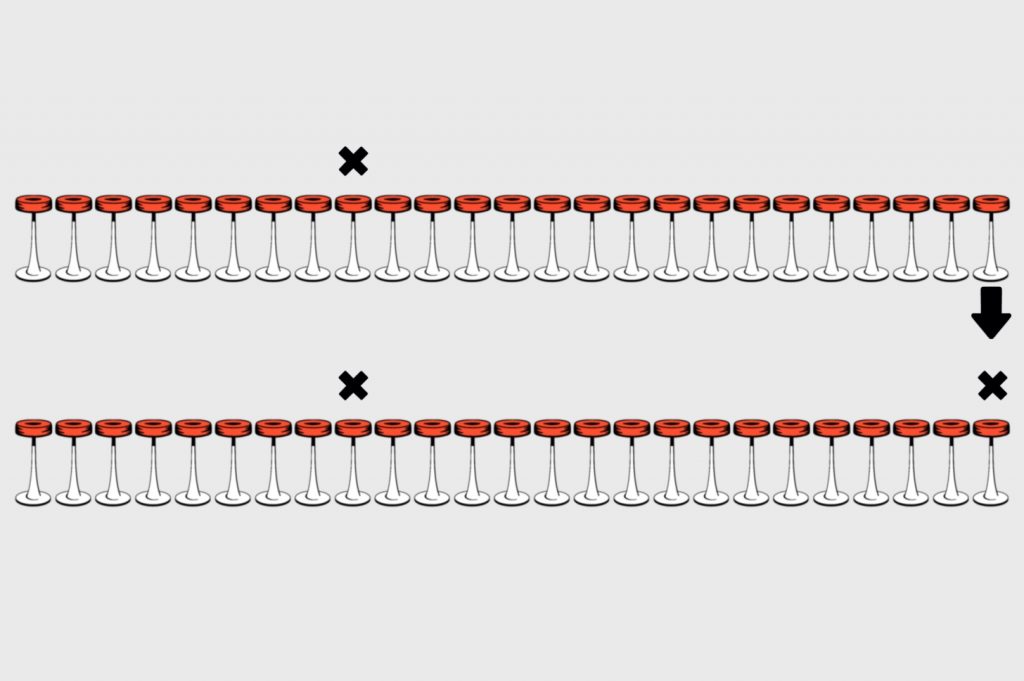
Получается, самого первого гостя бармен должен посадить на стул № 9.
Как так вышло? Просто посчитали от обратного. Программисты называют это Test-First Development, хех.