Задача из домашки для школьников начальных классов (ахахахаха, простите, но это действительно так):
Заполните пустые клетки цифрами от 0 до 9, используя каждую всего по одному разу, так, чтобы получились три верных равенства.
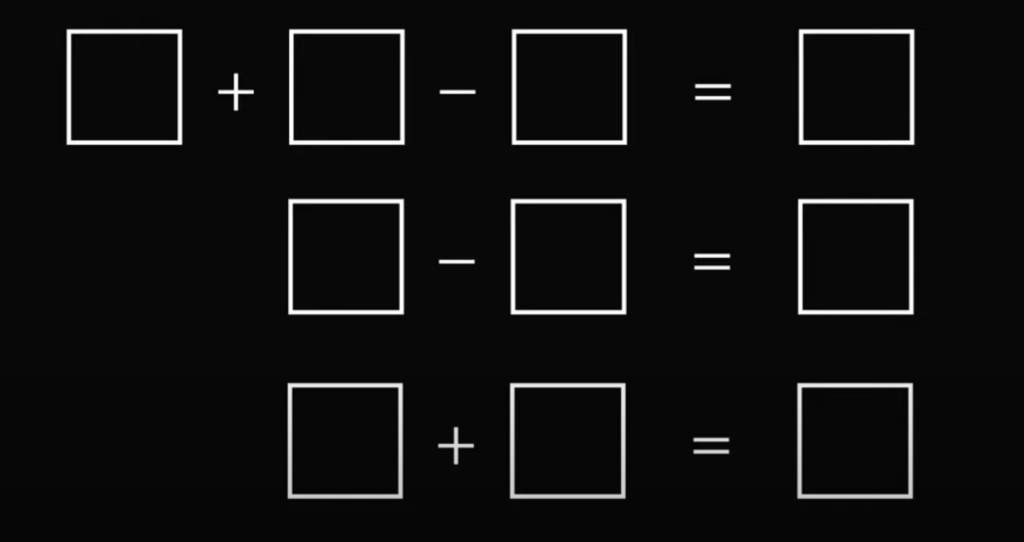
 Лучшие задачи на нестандартное и логическое мышление
Лучшие задачи на нестандартное и логическое мышление Сложная задача по простой математике для взрослых
Сложная задача по простой математике для взрослых Взрослая задача про монеты со сложными условиями
Взрослая задача про монеты со сложными условиями Две задачи про монеты для людей с нестандартным мышлением
Две задачи про монеты для людей с нестандартным мышлением Задача про границы, где вам нужно выйти за них, чтобы её решить
Задача про границы, где вам нужно выйти за них, чтобы её решить Задача на логику: что в какой коробке?
Задача на логику: что в какой коробке?Если думаете, что её можно решить простым подбором — не вопрос, но учтите, что всего там 3 628 800 комбинаций.
Удачи :)
Простого решения не будет, простите. Только сложное ↓
Сейчас будет очень нестандартное решение, мы предупредили.
Итак, представим, что вы уже провели какое-то время в попытках самостоятельно подставить разные цифры в пустые клетки, чтобы всё сошлось, но у вас не получилось. Давайте разберёмся, что могло пойти не так и что с этим делать.
Вместо того, чтобы подставлять конкретные значения, заполним квадратики буквами, где каждая буква означает какую-то цифру:
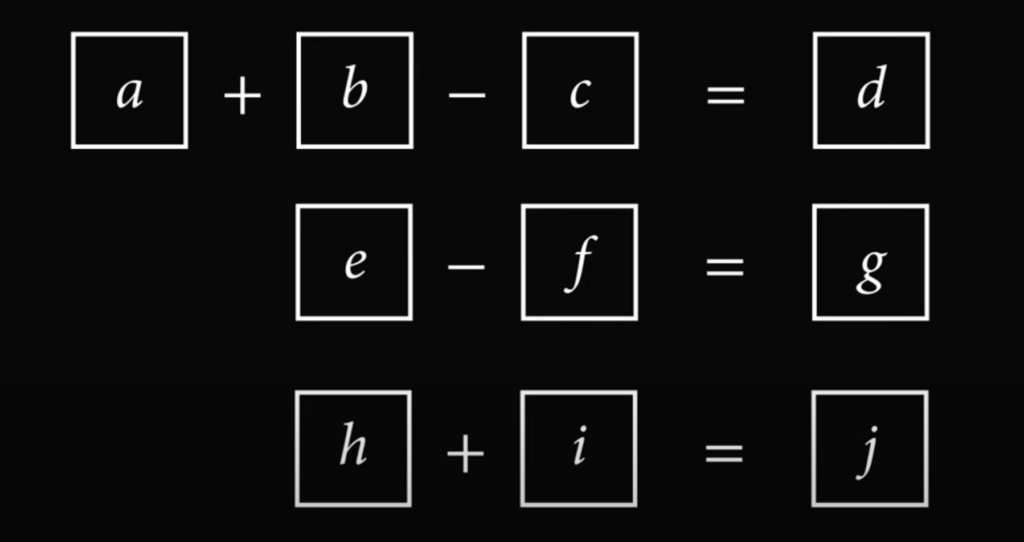
Теперь мы можем составить три равенства:
a + b − c = d
e − f = g
h + i = j
Перенесём всё так, чтобы у нас были только суммы:
a + b = c + d
e = f + g
h + i = j
Так как у нас левые и правые части равны между собой, сложим их по группам — всё, что слева, и всё, что справа. Результаты сложения, само собой, тоже будут равны между собой:
a + b + e + h + i = c + d + f + g + j (равенство 1)
Запомним это и теперь возьмём изначальные 10 цифр:
a + b + c + d + e + f + g + h + i + j
По условию это все 10 цифр от 0 до 9 — найдём тоже их сумму:
0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
Получается, что:
a + b + c + d + e + f + g + h + i + j = 45 (равенство 2)
Но мы выяснили раньше, что:
a + b + e + h + i = c + d + f + g + j
Подставим в равенство 2 вместо суммы чисел ( c + d + f + g + j) другую сумму — (a + b + e + h + i), что позволяет сделать нам равенство 1. Посмотрим, что получилось:
a + b + c + d + e + f + g + h + i + j = 45
a + b + e + h + i + (c + d + f + g + j) = 45
a + b + e + h + i + (a + b + e + h + i) = 45
2 × (a + b + e + h + i) = 45
(a + b + e + h + i) = 45 / 2 = 22,5
Но по условию у нас есть только целые цифры и сумма любых пяти из них никак не может дать в результате дробное число — 22,5.
Получается, эта задача в принципе не имеет решения!
*Как обычно бывает в школе, задание со звёздочкой: какой один знак нужно поменять между квадратами в изначальном условии, чтобы этот пример имел решение?
Ответ напишите в комментариях.










