Эта задачка на нестандартное мышление, логику и гибкость ума. Попробуйте поразмышлять над ней самостоятельно, и если не получится — открывайте наше решение. Подобные задачи здорово упорядочивают ум.
Итак, задача.
Программист сдал начальнику отчёт о выполненных задачах за год. Перед этим над ним все смеялись, потому что за любые пять месяцев подряд в течение года он закрывал меньше задач, чем надо было по плану. Но когда начальник принял отчёт, все узнали, что на самом деле программист перевыполнил план и получил премию.
Как это могло произойти?
Эта задача из тех, где мы уже знаем ответ, но не знаем решения. Наша цель — придумать такое решение, чтобы оно полностью подходило по условиям и приводило к нужному ответу.
В нашем случае нужно подобрать такое количество выполненных задач и задач из трекера, чтобы за каждые 5 месяцев подряд сумма задач из трекера была больше, а за год — меньше, чем количество выполненных. Или если посмотреть наоборот: чтобы за каждые пять месяцев подряд сумма выполненных задач была меньше плана, а по итогам года — больше.
Допустим, мидл каждый месяц выполнял по 10 задач, а сколько нужно было — мы не знаем. Тогда его работа выглядит так:

Получается, что за год он сделал 120 задач, и в трекере должно получиться меньше, чем 120.
Теперь посмотрим на нижний ряд — количество задач в трекере на этот месяц. Наш период — 5 месяцев, поэтому посмотрим, как можно сделать так, чтобы эти периоды пересекались как можно меньше:
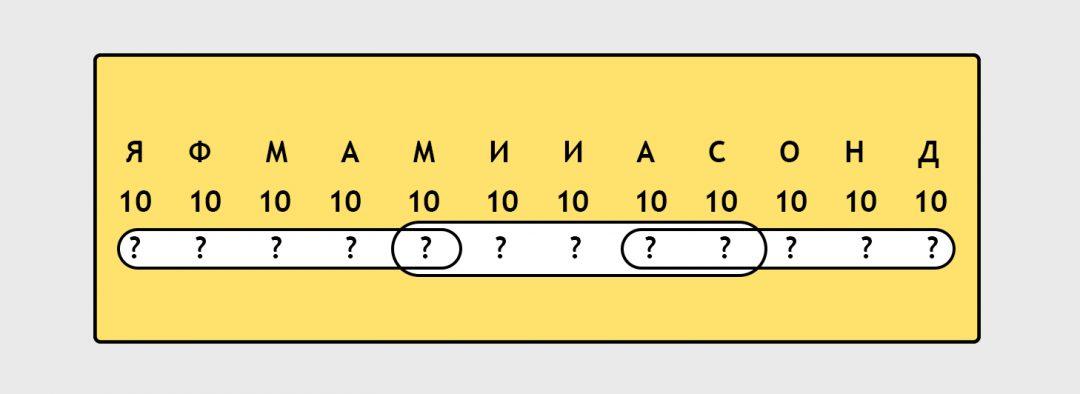
В точках пересечения у нас будет математическая магия, поэтому запомним, на каких местах они получились. В идеале нам нужно получить такую картину: в этих точках пересечения стоят большие числа, а во всех остальных — единицы, чтобы при сдвигании периода влево или вправо они как можно меньше влияли на общую сумму. Проставим единицы в начале и конце и посмотрим, что получилось:

Теперь возьмём первые 5 месяцев: выполнено 50 задач, а поставлено — 4. Нам нужно, чтобы за 5 месяцев поставленных было больше, чем выполненных, значит нам нужно число, больше, чем 50, значит это будет 51. Считаем, что будет на месте первого знака вопроса: 51 − 4 = 47. Подставляем это число на место первого знака вопроса:

То же самое делаем с правой стороны:
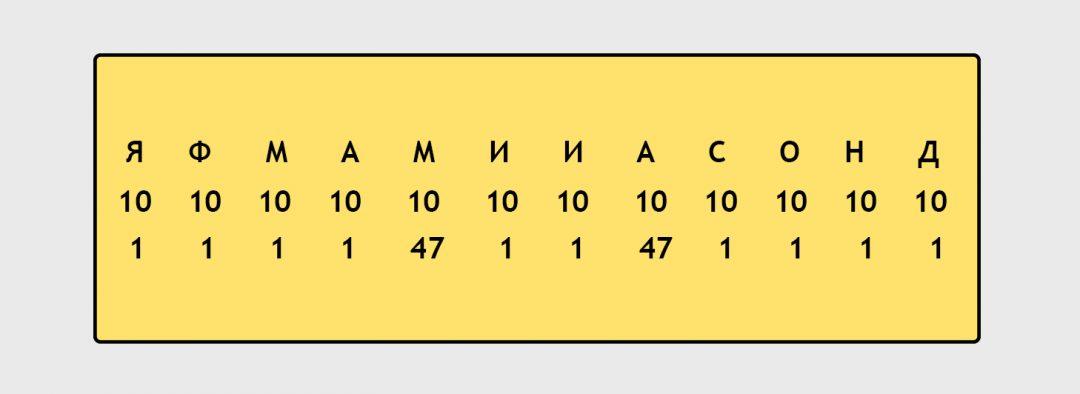
Красиво и симметрично. Обратите внимание, что в период с мая по сентябрь мидлу поставили 97 задач, а он сделал всего 50. Теперь проверяем, что у нас получается по итогу года.
Выполнено: 10 × 12 = 120 задач
Поставлено в баг-трекере: 1 + 1 + 1 + 1 + 47 + 1 + 1 + 47 + 1 + 1 + 1 + 1 = 104 задачи.
То, что нам нужно: за любые 5 месяцев мидл делал меньше, чем нужно, а за год — сделал больше и перевыполнил план. Красавчик. Математик. Логик. Практик.