Помните задачу про мышей и испорченную партию лекарства? Там у нас было 10 мышей и 1000 пробирок. В одной из пробирок яд. Нужно проверить, в какой пробирке яд, за минимальное количество дней.
Классическое решение — начать делить пробирки по количеству мышей. Например, сначала разделить пробирки на 10 групп по 100; взять из каждой по капле; скормить мышам. Одна мышь умрёт — тогда эту группу пробирок делим снова на оставшихся мышей. Так за три-четыре деления мы найдём пробирку с ядом.
Но что если отравленную пробирку надо найти за одно измерение? Возможно ли это? Давайте посмотрим.
Чтобы найти пробирку с ядом за один день, нам надо призвать на помощь двоичную систему счисления. Но для начала разберёмся с привычной — десятичной.
Десятичная система счисления
Она самая знакомая из всех, и мы ей пользуемся каждый день. В её основе — 10 цифр, от 0 до 9, поэтому она и называется десятичной.
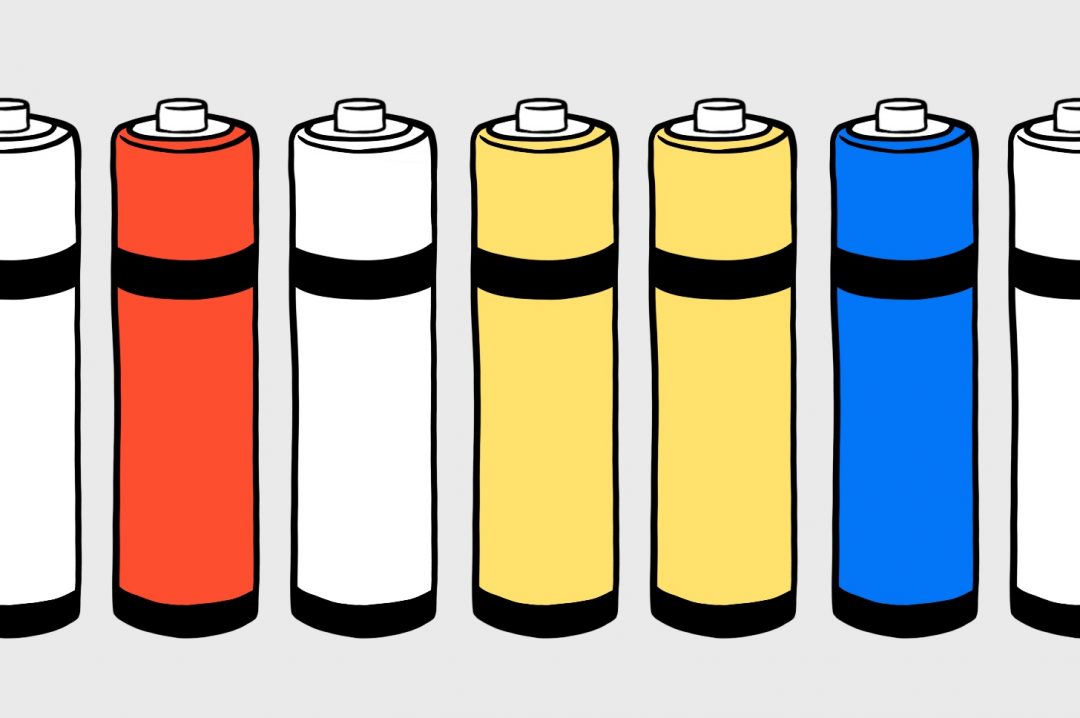
Мы пользуемся десятичной системой, особо не рефлексируя. Например, мы видим число 436 — мы автоматически его раскладываем: четыре сотни + три десятка + шесть.
Только что мы разложили число на разряды: 4 — это разряд сотен, 3 — разряд десятков, 6 — разряд единиц. Получается, что:
436 = (4 × 100) + (3 × 10) + (6 × 1)
436 = (4 × 10²) + (3 × 10¹) + (6 × 10 в нулевой степени)
Получается, что наша десятичная запись числа — это просто краткая форма записи длинного выражения, где какие-то числа умножаются на десятки в разных степенях.
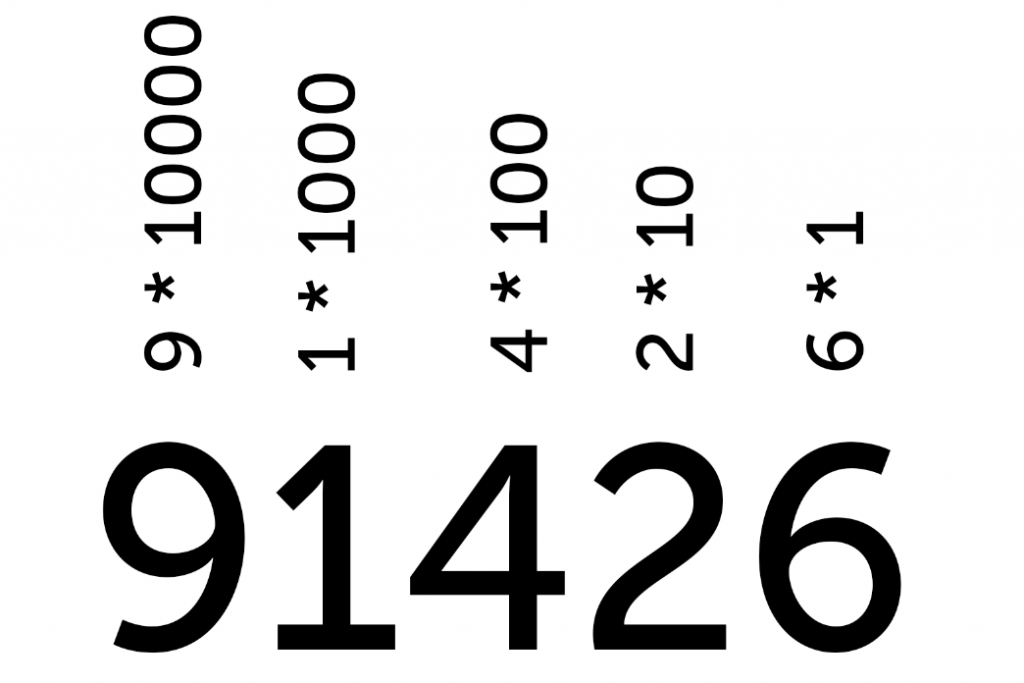
Двоичная система
Двоичная система — это то же самое, только вместо десятки — двойка. Вместо степеней десятки мы используем степени двойки. Вместо десяти цифр от 0 до 9 мы используем две: 0 и 1.
Чтобы перевести числа из двоичной системы счисления в десятичную, нужно то же самое, что и раньше: возводить двойку в степень разряда и умножать на 0 или 1. Рассмотрим на примере:
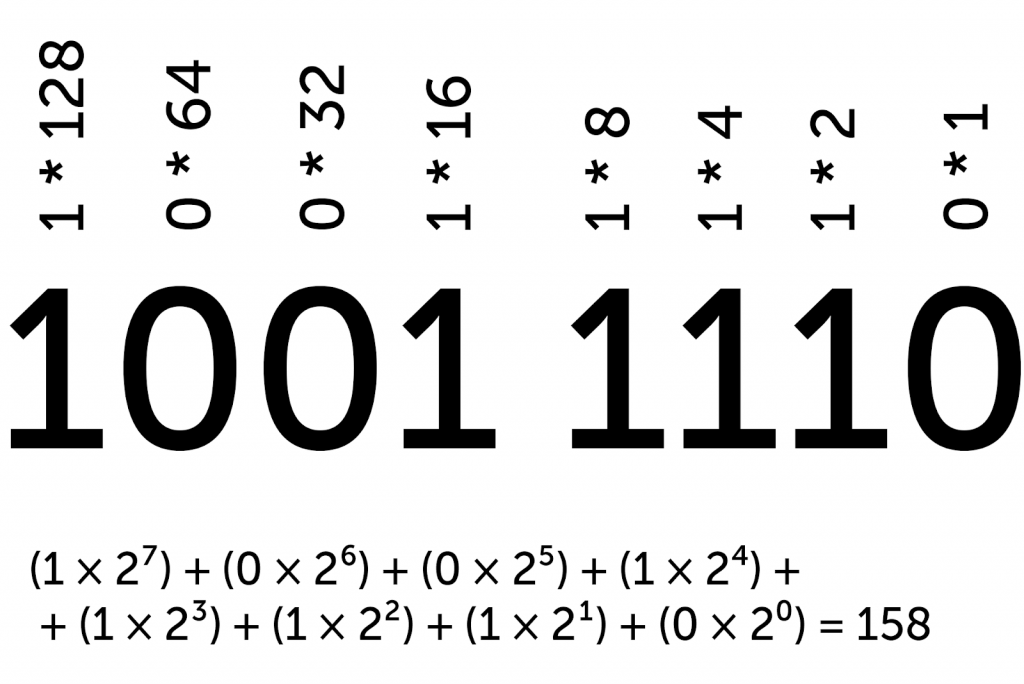
Любое десятичное число можно представить в виде двоичного, и наоборот. Теперь попробуем использовать это знание в решении задачи.
Битовая глубина
У нас 1000 пробирок. Запишем это число в двоичной системе счисления:
1000 в десятичной = 1111101000 в двоичной
Это максимальное число, которое нам понадобится при нумерации, и оно состоит из 10 нолей и единиц. Получается, что битовая глубина решения этой задачи — 10. А у нас как раз 10 мышей. Это и будем использовать при расчётах.
Немного магии
Зная, что у нас 10 бит на число, пронумеруем каждую пробирку таким образом:
1 — 0000000001
2 — 0000000010
3 — 0000000011
4 — 0000000100
...
999 — 1111100111
1000 — 1111101000
Затем расставляем мышей в клетки по порядку, чтобы они никуда не бегали и всегда оставались на своих местах. Пусть клетки стоят слева направо.
А теперь начинается магия. Берём каждую пробирку и смотрим, на каких местах стоят единицы. Мышам в этих клетках даём каплю вещества:
первая пробирка: 0000000001 — даём каплю мыши в самой правой клетке
вторая пробирка: 0000000010 — даём каплю мыши во второй клетке справа
третья пробирка: 0000000011 — даём по капле двум мышам из первой и второй клеток справа
четвёртая пробирка: 0000000100 — даём каплю мыши в третьей клетке справа
...
999 пробирка: 1111100111 — даём по капле мышам из первых пяти клеток слева, пропускаем две клетки, дальше капаем трём оставшимся
Таким образом, каждая пробирка получила свою уникальную комбинацию из мышей. И на следующий день, когда часть мышей умрёт, мы сразу узнаем номер пробирки с ядом: оставшихся в живых мышей запишем как 0, а погибших — как 1.
Например, наутро мы заметили, что шесть мышей слева и одна справа живы, остальные три мертвы. Запишем это в двоичной системе:
0000001110
Переведём вручную или на калькуляторе это в десятичную систему и получим число 14. Это и есть номер нашей пробирки с ядом.
В чём секрет
Секрет в том, что комбинация нолей и единиц уникальна для каждой пробирки. И раз мы даём по капле тем мышам, которые соответствуют единице, то если в них будет яд, помечать их тоже надо единицами, чтобы восстановить картину. Комбинация погибших мышей из-за своей уникальности и укажет нам на номер пробирки с ядом.