Представьте, что вам предложили пари:
- Вы выбираете один из двух вариантов игры с мячом.
- Футболист играет в предложенную вами игру.
- Если футболист выигрывает, вы и футболист получаете деньги. Если нет — никто ничего не получает.
Первый вариант игры — ударить по мячу один раз. Если мяч попадёт в ворота — вы выиграли.
Второй вариант игры — ударить по мячу три раза. Если хотя бы два раза из трёх мяч попал в ворота — вы выиграли.
За выигрыш в любом варианте вам заплатят 50 000 рублей. Какой вариант игры лучше выбрать и почему? Вы знаете, что в среднем футболист забивает три мяча из пяти, но в истории игрока бывало и много непопаданий подряд.
Вероятность
В таких задачах всё зависит от вероятностей — насколько возможно, что это всё произойдёт. Вероятность чаще всего измеряется в процентах: чем они выше, тем вероятнее случится нужное нам событие. Например, когда мы подкидываем монету, вероятность того, что выпадет орёл — 50%. Это значит, что в половине случаев действительно выпадет орёл. А вероятность бросить кубик и сразу получить 6 очков — около 17% или ⅙ , потому что у кубика 6 равноценных граней.
Давайте обозначим символом р вероятность того, что футболист при любом ударе забивает гол в ворота. Получается, в первом варианте наши шансы получить деньги тоже равны р, потому что футболист должен забить с первого раза. Так как вероятность — это число от 0% до 100% (это то же самое, что от 0 до 1), мы имеем два выражения:
р — вероятность, что футболист попадёт в ворота.
(1 — р) — вероятность, что футболист промахнётся.
Если мы выбрали первую игру с одним ударом, вероятность выигрыша равна вероятности попадания в ворота, то есть р. Зная, что футболист попадает три раза из пяти, мы можем смело сказать: вероятность выигрыша в первой игре — 60%. Неплохая вероятность и пока всё очевидно.
А что со второй игрой? Стоит ли пробовать её, если мы знаем вероятность победы в первой? Давайте хотя бы сравним.
Для второго варианта игры есть восемь разных путей развития событий — комбинаций попаданий и непопаданий в ворота. Давайте занесём их в таблицу, и если в какой-то попытке мы попали в ворота — поставим на этом месте галочку. Рядом запишем значения вероятностей этих событий. Вероятности перемножаются:
| Первый удар | Второй | Третий | Вероятность | Выиграли? |
| (1 - p) × (1 - p) × (1 - p) | Нет | |||
| ✓ | (1 - p) × (1 - p) × р | Нет | ||
| ✓ | (1 - p) × p × (1 - p) | Нет | ||
| ✓ | ✓ | (1 - p) × р × р | Да | |
| ✓ | p × (1 - p) × (1 - p) | Нет | ||
| ✓ | ✓ | p × (1 - p) × р | Да | |
| ✓ | ✓ | p × p × (1 - p) | Да | |
| ✓ | ✓ | ✓ | p × p × p | Да |
В таблице приведены все варианты развития событий, никаких других быть не может. Судя по таблице, из восьми вариантов развития событий мы выигрываем в четырёх. Рассмотрим варианты выигрыша.
В трёх выигрышных случаях футболист промахивается один раз. Вероятности у этих трёх сценариев:
(1 — p) × р × р
p × (1 — p) × р
p × p × (1 — p)
Заметили, что все эти формулы можно привести к одному виду?
p × p × (1 — p)
А эта формула, в свою очередь, приводится к такому виду:
p × p × (1 — p)
p² × (1 — p)
p² — p³
В четвёртом призовом случае вы забьёте мяч три раза подряд, и вероятность этого такая:
p × p × p = p³
Чтобы узнать общую вероятность выигрыша, нужно сложить первые три и четвёртую. Для этого достаточно математики седьмого класса. Сделаем это пошагово:
(p² — p³) × 3 + p³
3p² — 3p³ + p³
3p² — 2p³ — это вероятность нашего выигрыша во второй игре.
Мы помним, что вероятность выигрыша в первой игре равна p. Осталось выяснить, что в нашем случае больше: р или 3р² — 2р³. Та игра, где вероятность выше, нам и нужна.
Математическое ожидание
Давайте на секунду забудем, что мы знаем точность нашего футболиста. Мы не в курсе, что он забивает 3 пенальти из 5. Мы лишь знаем, что его вероятность попадания в ворота равна р, при этом если p = 0, мы ничего не выиграем, а если p = 100% (то есть 1), мы точно выиграем 50 000 рублей. Осталось понять, какова вероятность выигрыша в промежуточных сценариях между 0% и 100%. Для этого понадобится математическое ожидание.
Математическое ожидание — это произведение результата на вероятность его получения. В нашем случае — произведение денежного приза на вероятность его получения. Это число не имеет никакого отношения к реальности — по правилам игры при точности футболиста 50% мы не получим 25 000 рублей. Мы считаем математическое ожидание, только чтобы оценить свои шансы.
В первом варианте игры наше математическое ожидание равно 50 000 × р, во втором оно же равно 50 000 × (3р² — 2р³).
Чтобы понять, какое ожидание лучше, давайте нарисуем два графика. Они покажут зависимость результата математического ожидания каждого случая от вероятности того, что футболист забьёт гол. Проще говоря, мы возьмём вероятность гола в 1% и посмотрим, чему будет равно математическое ожидание в обоих случаях. Потом возьмём вероятность 2% и тоже посмотрим на результат ожидания. Потом вероятности 3%, 4%, 5% и так далее. Когда дойдём до 100%, картина будет ясна:
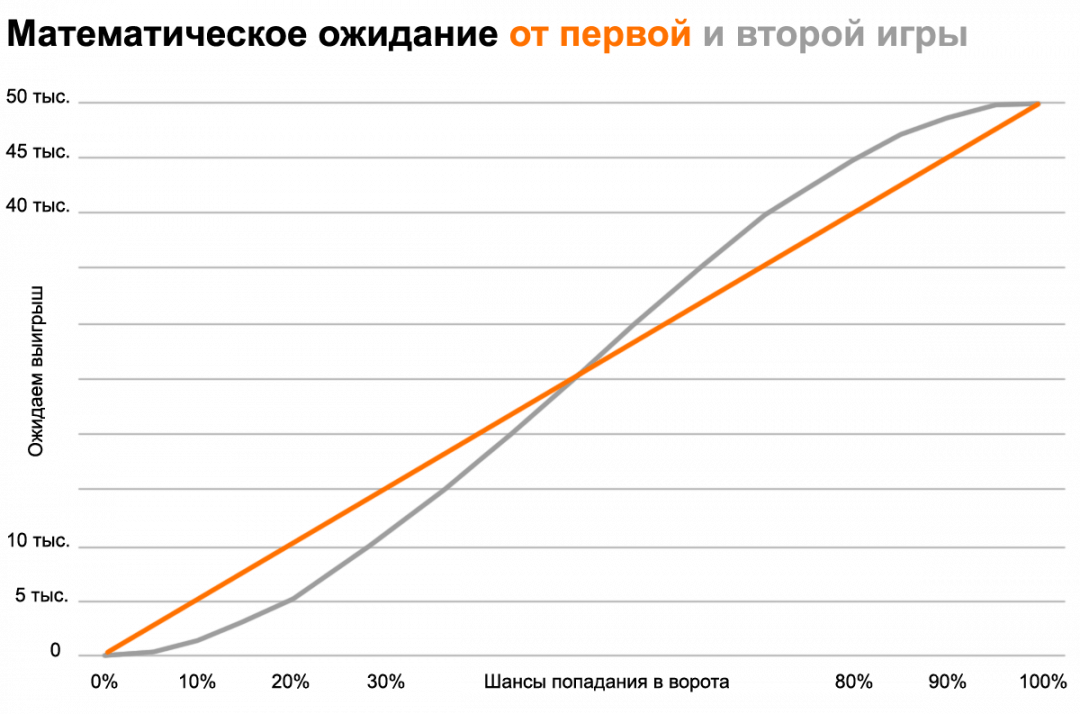
Оранжевая линия показывает график математического ожидания от первого варианта игры. Тут всё понятно: чем точнее футболист бьёт по воротам, тем больше вероятность, что мы выиграем, связь линейная.
Серая линия показывает наши шансы в варианте игры с тремя ударами. Тут начинается самое интересное:
Если точность футболиста меньше 50%, то наше математическое ожидание от второго варианта игры ниже, чем от первого. То есть мазила скорее промахнётся, чем попадёт. И с точки зрения теории вероятностей лучше бы он ударил один раз, чем три.
Если точность футболиста больше 50%, то первая игра даёт более низкое математическое ожидание, чем вторая.
Графики пересекаются ровно посередине, в вероятности 50%. Это значит, что если бы у нашего футболиста всегда было 5 попаданий из десяти, то вероятность выиграть в любой из двух игр у нас одинаковая.
Это можно объяснить ещё и так. Если футболист забивает плохо, то на победу можно не рассчитывать. Максимум, что случится — вам повезёт, и футболист при ударе случайно забьёт гол. Так как такая удача случится, скорее всего, только один раз, то и выбрать в этом случае нужно вариант с одним ударом. А если футболист в целом неплох, то во второй игре у него больше шансов реабилитироваться и отыграться, поэтому нужно ставить на вторую игру.
И финальный штрих: так как мы знаем, что p = 60%, нам очень легко получить математические ожидания от двух игр, зная все вероятности:
Первая игра. Матожидание = 50 000 × 0,6 = 30 000
Вторая игра. Матожидание = 50 000 × (3 × 0,62 — 2 × 0,63) = 32 400
Матожидание от второй игры немного выше, чем от первой. Мы, конечно, не получим этих денег именно в таком виде. Но по этому числу мы видим, что вторая игра с точки зрения вероятностей нам выгоднее.
Важное о вероятностях
Рассчитывая вероятности, помните, что вероятность — это не гарантия. В момент игры может подуть сильный ветер, начаться дождь или футболист может быть мотивирован специально мазать мимо ворот (такое сплошь и рядом в теории игр). Вероятности работают только на больших выборках и в строго контролируемых условиях.
Например, нам могут предложить сыграть 100 игр в одинаковых условиях, давая футболисту возможность достаточно отдыхать после каждой игры. Тогда математическое ожидание будет иметь практический смысл.
Но если нам предложат 100 игр подряд на открытом воздухе, после каждой из которых футболист не будет отдыхать, то мы получим как минимум два эффекта:
- футболист будет уставать, его показатель точности со временем снизится;
- за время ста игр может смениться температура воздуха и ветер, что повлияет на точность.
Поэтому математическое ожидание не является гарантией выигрыша. Чем применять матожидание в ставках на спорт или в казино, лучше найти высокооплачиваемую работу программистом.