Мы начали разбирать большую дисциплину — алгоритмы и структуры данных. В прошлый раз рассказали в общих чертах про несколько основных видов алгоритмов, а сегодня возьмём конкретно один из них — алгоритмы сортировки. Разберём их подробнее: зачем нужны, в чём принцип работы и какие механизмы там используются.
Напомним: что такое алгоритмы
Алгоритм — это пошаговая операция, которая должна привести к какому-то результату.
Такие операции могут быть в обычной жизни. Например, упрощённый алгоритм написания статьи в журнал «Код» будет выглядеть так:
- Выбрать тему для статьи.
- Собрать источники информации.
- Составить план.
- Написать драфт статьи.
- Подобрать иллюстрации.
- Утвердить финальную версию с главным редактором.
- Передать статью в вёрстку.
Компьютерные алгоритмы работают по такому же принципу, только решают задачи в коде, а не реальности. Мы пишем набор указаний для компьютера, программа им следует и выдаёт результат. Чтобы результат соответствовал ожиданиям, нужно написать работающий алгоритм с правильными действиями.
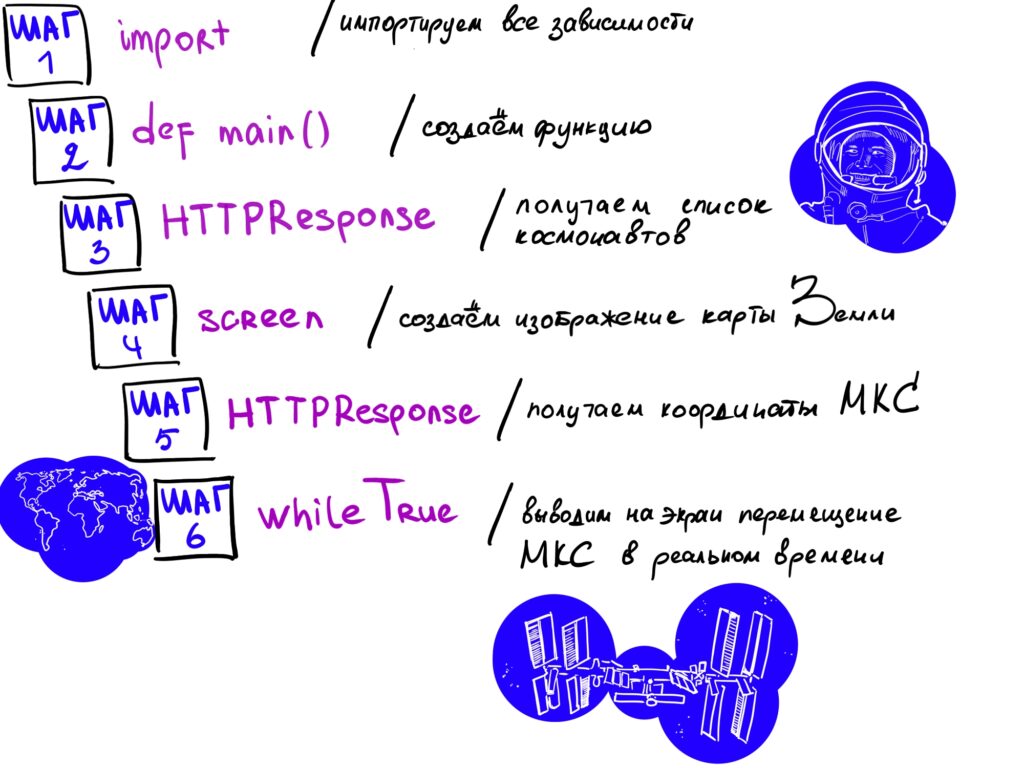
Вот как может выглядеть упрощённый и вольно записанный алгоритм работы программы, которая отображает на карте Земли перемещение МКС в реальном времени (этот проект мы тоже делали в «Коде», посмотрите, там много интересного):
Зачем нужны алгоритмы
Любая программа — какой-то алгоритм по работе с кусочками памяти компьютера, структурами данных.
Но когда говорят о компьютерных алгоритмах, обычно имеют в виду шаблонные шаги, которые можно применить для решения уже устоявшихся задач: сортировки большого количества данных, поиска нужного элемента и других.
Как считается сложность алгоритмов (и алгоритмов сортировки тоже)
У всех алгоритмов есть основная оценка — сложность, которая обозначается большой буквой O. Это категория скорости увеличения времени работы алгоритма при увеличении входных данных задачи.
Например, простой алгоритм по получению элемента по номеру из списка будет иметь сложность, равную 1. Сколько бы элементов не было в списке, получение одного из них всегда займёт ровно одно действие. Сложность такого алгоритма записывается так: O(1).
Если для получения результата алгоритму нужно обработать каждый элемент массива, то его сложность будет равна количеству элементов. Сколько элементов — столько и действий. Это сложность O(n).
В алгоритмах сортировки всё работает точно так же: зная оценку сложности алгоритма, мы можем заранее понять, будет ли он работать достаточно быстро для нашей задачи или лучше выбрать другой алгоритм.
Вот основные категории сложности алгоритмов:
- О(1) — константная сложность, которая всегда равна одному количеству действий;
- О(n) — линейная сложность, равна количеству входных элементов;
- О(log n) — логарифмическая сложность, считается как логарифм от количества входных данных;
- О(n2) — квадратичная сложность, равна квадрату количества элементов на входе;
- О(n3) — кубическая сложность, растёт в кубической прогрессии;
- О(n!) — факториальная сложность, растёт быстрее всех других вариантов.
Если у алгоритмов одинаковые сложности, это не значит, что они работают одинаково. Но график зависимости времени работы от количества входных данных чаще всего у них будет одинаковый.
Что делают алгоритмы сортировки
Сортировочные алгоритмы расставляют элементы в наборе данных по какому-то признаку: возрастанию, цвету, алфавиту.
Во всех популярных языках программирования, таких как Python, JavaScript или C++, есть встроенные функции сортировки. Но иногда такие готовые решения не подходят, например они могут быть недостаточно эффективными или не работать со сложными типами данных.
Самый простой вариант алгоритма расставляет предметы по одному признаку. Но часто у элементов может быть больше одной характеристики для сортировки:
- Книги можно расставлять по автору, жанру или цвету обложки.
- Игры в базах данных можно отсортировать по названию, дате выхода, компании-разработчику или издателю.
- Товары на маркетплейсах можно расположить по цене, дате доставки, рейтингу популярности среди покупателей.
Для работы с несколькими признаками алгоритмы сортировки используют индексы — маркировки товара по каждой характеристике. Это немного усложняет работу и делает программу медленнее, но в итоге поиск занимает меньше времени.
Алгоритмы сортировки на практике
Часто говорят, что польза от алгоритмов сортировки в том, что их знание поможет получить работу, показав эти знания на собеседовании. Но в реальности всё немного сложнее.
Даже если в реальном коде эти алгоритмы применяются редко, они помогают начать думать как разработчик и в целом лучше понимать принципы работы компьютерных программ.
Также алгоритмы сортировки или их принципы всё же используются для решения разных задач:
- в базах данных — для упорядочивания и ускорения чтения записей;
- для сортировки потоковых данных, когда обычная сортировка не подходит;
- в анализе больших данных и машинном обучении — для предварительной обработки данных;
- в компьютерной графике — для упорядочивания объектов для рендеринга.
А ещё новые алгоритмы сортировки часто появлялись как решение настоящих практических задач, например:
- Сортировка Radix Sort появилась в конце 1800-х годов для физической сортировки перфокарт для переписи США. Она всё ещё используется из-за своей скорости.
- Сортировку слиянием изобрёл Джон фон Нейман для проверки компьютерных моделей.
- Timsort был изобретён для Python для быстрой сортировки последовательностей с учётом преимуществ других моделей.
- Интроспективная сортировка появилась как способ использовать скорость быстрой сортировки без худшего случая, когда входные данные требуют максимально возможного количества времени и ресурсов. Для быстрой сортировки худший случай приравнивает её по производительности к сортировке пузырьком.
- Исследование ограничений сортировки Shellsort было сложной математической проблемой, работа с ним продвигала науку.
Какие подходы используют алгоритмы сортировки
Каждая технология использует какую-то основную идею. Часто похожие подходы в разных алгоритмах говорят о том, что они имеют одинаковую сложность.
Вот несколько подходов, которые реализованы в некоторых популярных алгоритмах сортировки.
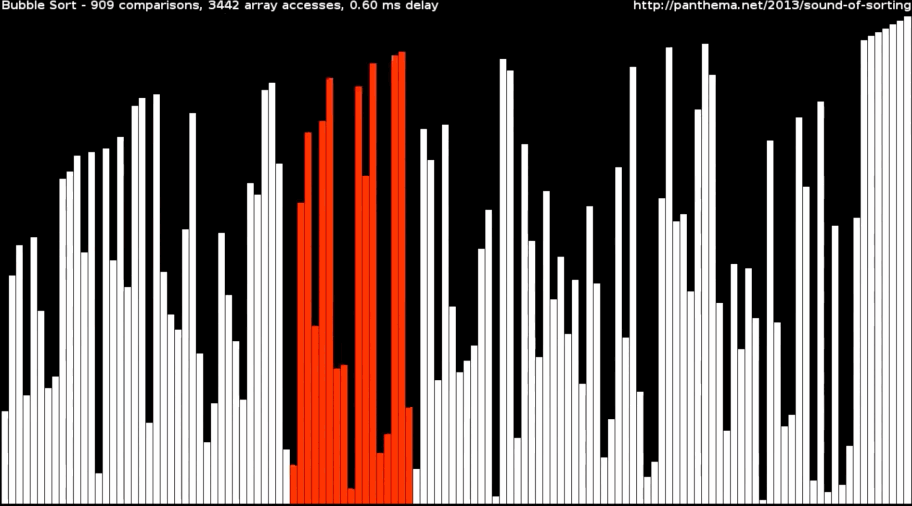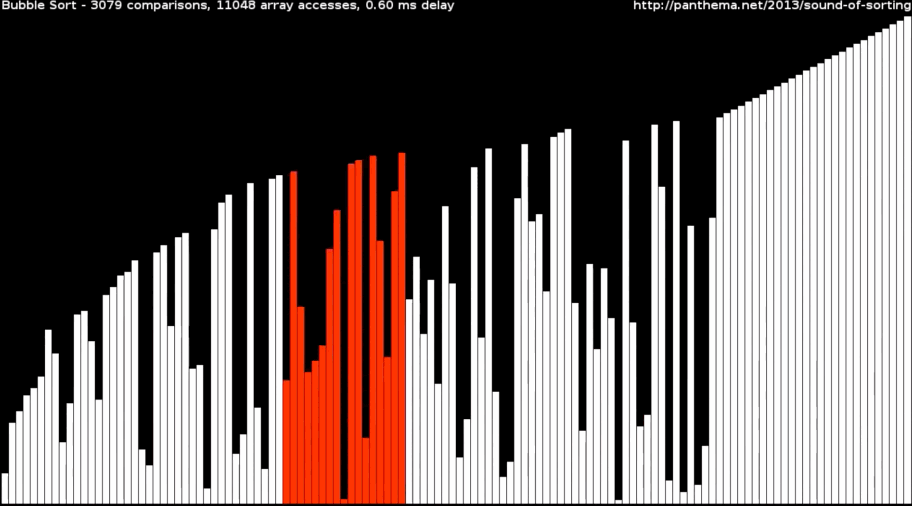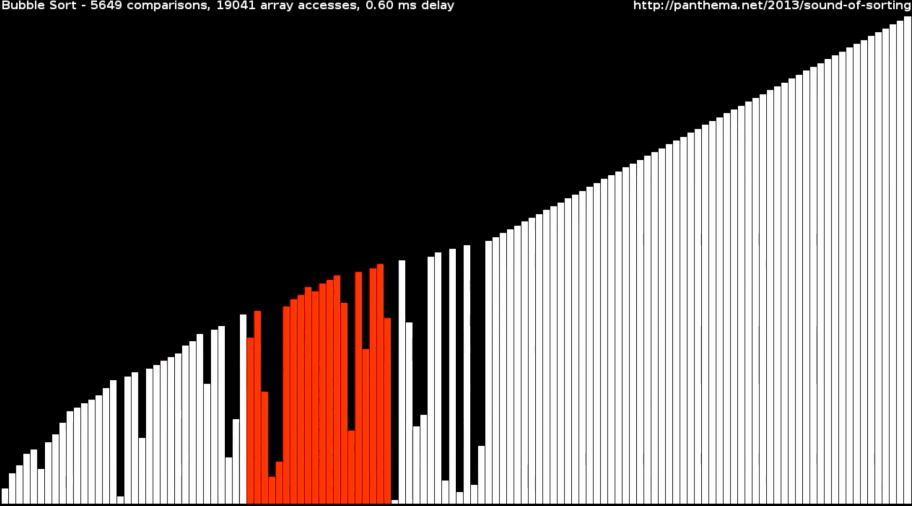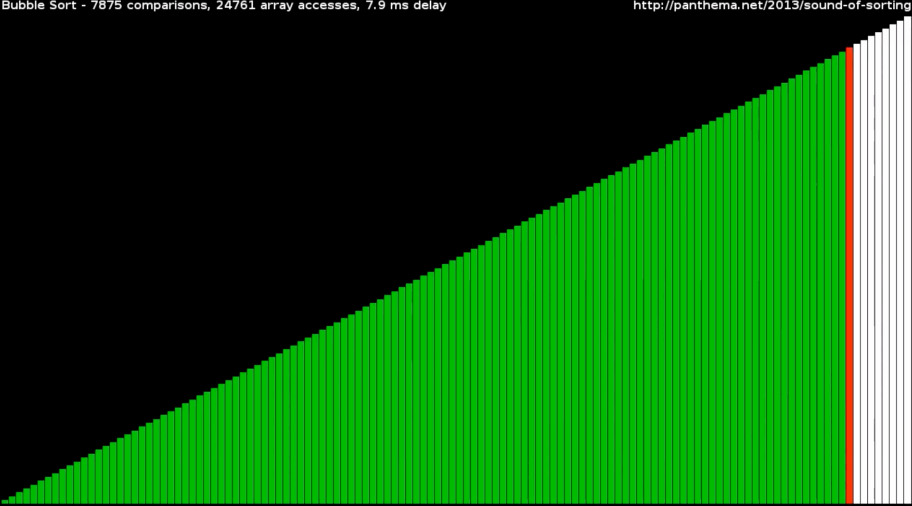
Инкрементальный подход. Суть в том, что мы постепенно строим частичное решение. Алгоритм циклично проходит по массиву данных, которые нужно отсортировать, и за один раз помещает одно значение в правильную позицию. Получается, что за каждый проход по массиву количество неотсортированных данных уменьшается на 1, а отсортированных, наоборот, увеличивается на 1.
Так работают сортировки пузырьком и выбором, если взять массив разных чисел и визуализировать их в виде столбиков разных размеров:
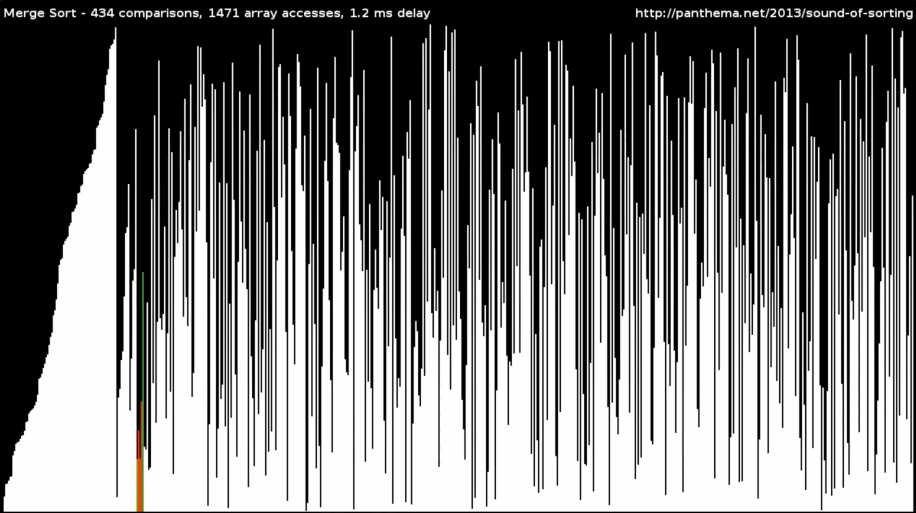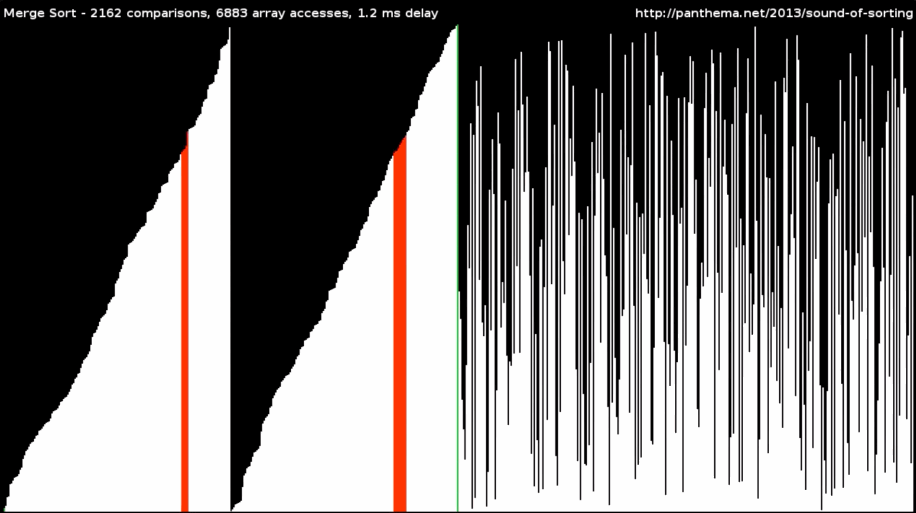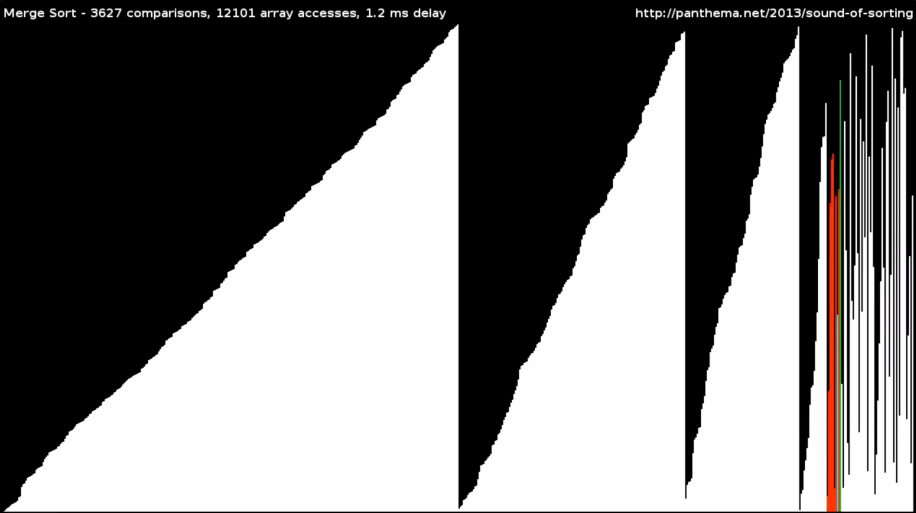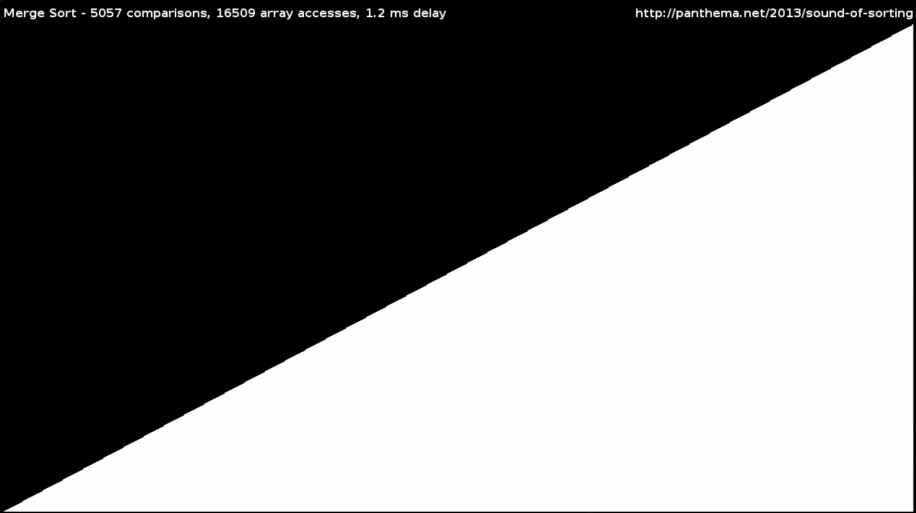
Разделяй и властвуй. Это принцип, при котором задача разделяется на небольшие подзадачи, после чего каждая из них решается отдельно. После этого решения совмещаются, чаще всего с помощью рекурсии. Рекурсия, если вкратце, — функция, которая вызывает сама себя до тех пор, пока не будет выполняться какое-то исходное условие. Например, пока все элементы не будут стоять по порядку.
Так работают сортировка слиянием и быстрая сортировка:
Разделение данных по признакам. Этот приём не работает с данными напрямую, а делит их по некоторым группам и работает уже с ними.
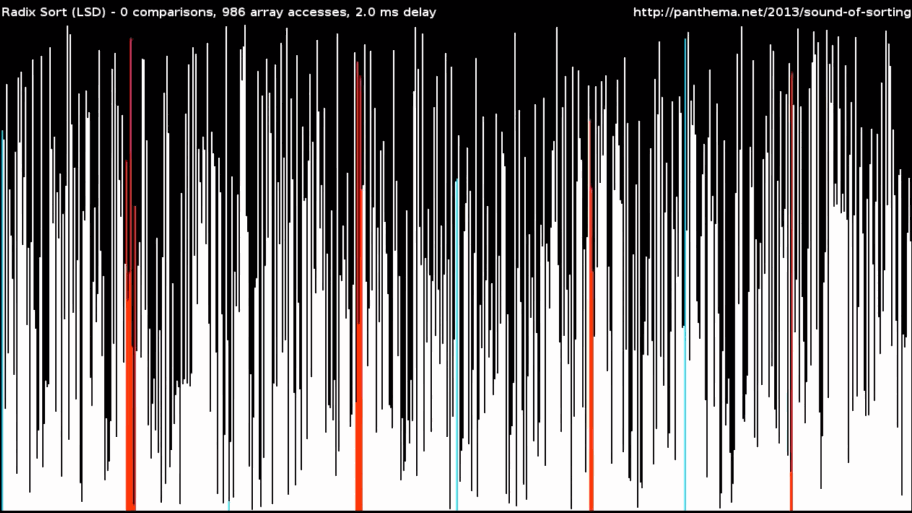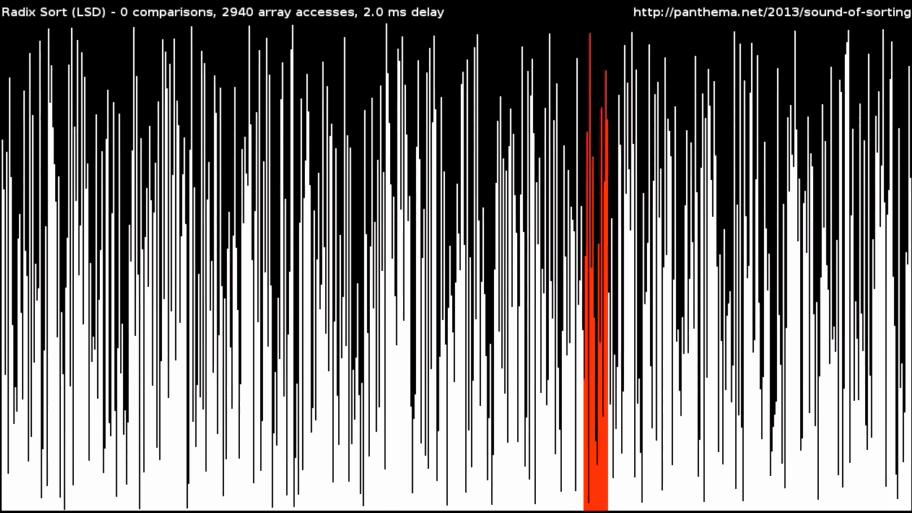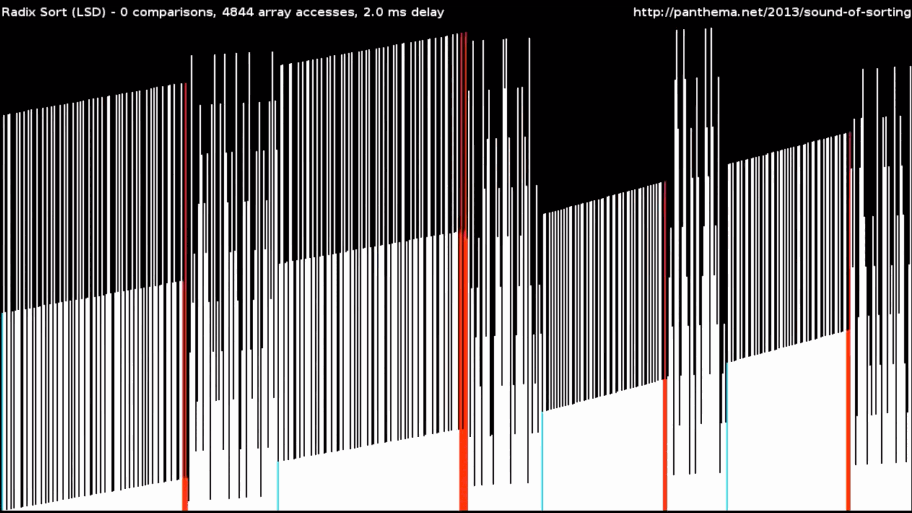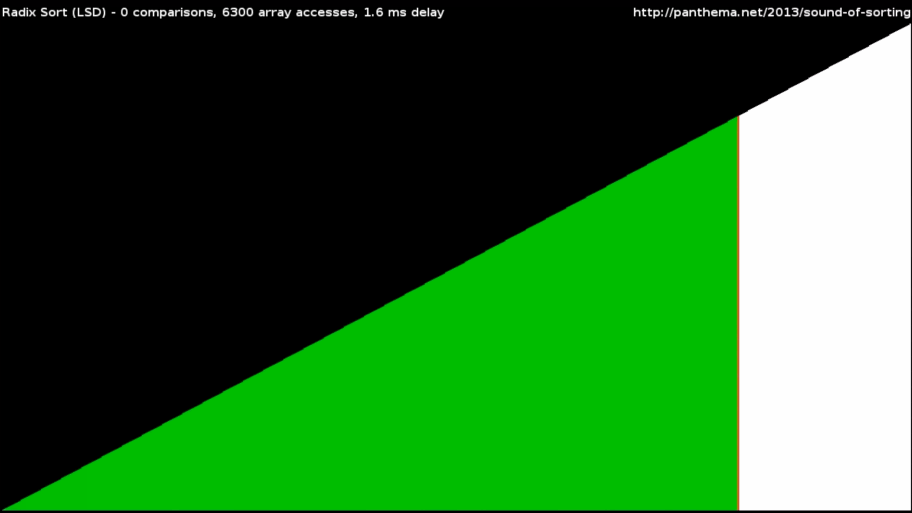
Пример — поразрядная сортировка, или Radix Sort. Этот алгоритм делит массив числовых данных по основаниям и разрядам и расставляет элементы в несколько подходов. Предварительное разделение позволяет работать быстро:
С чего начать учить
Мы уже разобрали подробно много алгоритмов сортировки, для начала почитайте про них:
Если все статьи вы уже перечитали и вам всё мало, пройдите курс по алгоритмам и структурам данных от Практикума. Там вы научитесь применять алгоритмы в коде и подготовитесь к техническому собеседованию.
Первый модуль — бесплатно.