Сегодня расскажем о регрессионном анализе. Этот метод используется в статистике и аналитике для прогнозирования — он помогает разобраться, как один показатель зависит от другого: есть ли между ними прямая связь, косвенная, ещё какая-то более сложная зависимость или они вообще не связаны.
Понимание методов анализа полезно не только аналитикам и специалистам Data Science, но и всем, кто работает с данными.
Определение регрессионного анализа
Официальное определение звучит так:
Набор статистических методов исследования влияния одной или нескольких независимых переменных X1, X2, … Xp на зависимую переменную Y.
Простой смысл в том, что у нас несколько X-показателей, которые можно менять и смотреть, что от этого будет с показателем Y. Статистический регрессионный анализ заключается в определении этой зависимости, есть она или нет, а если есть — то как одно влияет на другое.
Основные понятия
Чтобы было яснее, разберём несколько основных терминов регрессионного анализа. Для наглядности рассматривать будем связь зарплаты и работы.
Зависимая, или целевая, переменная — это наша цель, меняющийся показатель. Весь смысл регрессионного анализа в том, чтобы понять, как именно она меняется. Если мы изучаем зависимость зарплаты от работы, то зарплата будет нашей целевой переменной.
Независимая переменная, предиктор или фактор — это всё разные названия показателей, которые можно менять и следить за изменением целевой переменной. Например, можно работать больше, меньше или вообще сменить работу — и смотреть на результаты в зависимой переменной.
Свободный член, константа — показатель, который не меняется в конкретном случае. Например, мы строим модель годового дохода человека, который держит портфель акций. При этом какой бы ни была связь работы и зарплаты, к финальному доходу будет всегда прибавляться небольшой процент от инвестиций. В другой модели этих инвестиций может не быть.
Коэффициенты регрессии показывают, как сильно изменится зависимая переменная при изменении независимой на единицу. Например, коэффициент 2 показывает, что с каждым годом зарплата увеличивается на 2 независимых переменных.
Ошибкой в регрессионном анализе называют разницу между показаниями истинного результата и модели анализа. Если модель предсказала зарплату в 1 000 единиц, а на деле вышло только 950, то ошибка будет равна 50.
Модель регрессии — математическое уравнение, которое описывает связь независимой и зависимой переменных. В общем виде выглядит примерно так:
Y = a + bX + ϵ
Что есть что в этом уравнении:
Y— зависимая переменная;a— свободный член;b— коэффициент;X— независимая переменная;ϵ(читается как «эпсилон») — ошибка.
Цели и задачи регрессионного анализа
Конечной целью регрессионного анализа должен быть достоверный прогноз. Он будет заключаться в понимании: как вырастет или упадёт объём продаж, изменится ли успеваемость студентов в группе или что будет с рынком акций компании.
Для этого нужно решить несколько задач.
- Вывести модель. Это может быть уравнение, которое покажет связи между зависимыми и независимыми переменными, или программа с нужными функциями.
- Найти связанные между собой параметры модели.
- Объяснить, как именно они между собой связаны.
- Проанализировать ошибки.
- Проверить качество модели и оценить, насколько хорошо она предсказывает действительные показатели, и понимать связи между переменными.
Методы регрессионного анализа
Есть несколько основных методов, которые используют для построения модели.
Все методы различаются, потому что каждая ситуация тоже немного индивидуальная. Данные ведут себя по-разному, поэтому решение о том, какой метод подойдёт лучше всего для отдельной задачи, должен принимать опытный аналитик.
Иногда разные методы нужно совмещать, потому что каждый в отдельности приносит переменный успех. Поэтому чем больше техник знает специалист по работе с данными, тем глубже будет анализ.
Линейный регрессионный анализ
Самый простой метод, где мы пытаемся провести прямую линию через данные, чтобы показать, как целевая переменная напрямую зависит от другой или других.
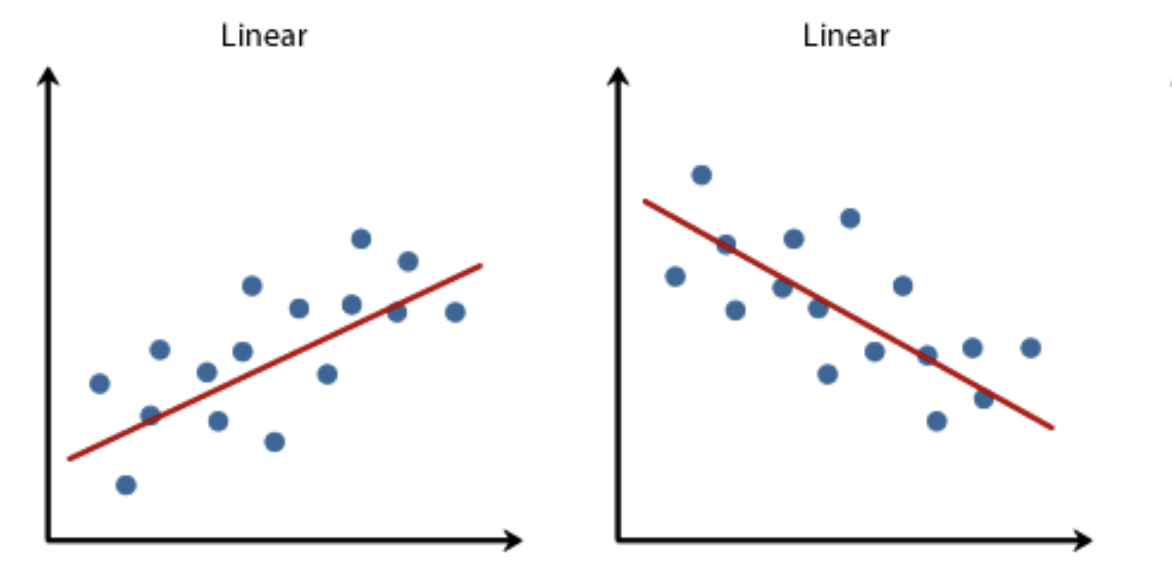
Если взять пример с работой, графиком будет являться прямая линия, которая ясно показывает: каждый год зарплата увеличивается на определённую сумму.
Полиномиальный регрессионный анализ
Более сложный метод описания зависимости, когда она не укладывается в прямую линию. Полиномиальная регрессия позволяет строить более гибкие линии.
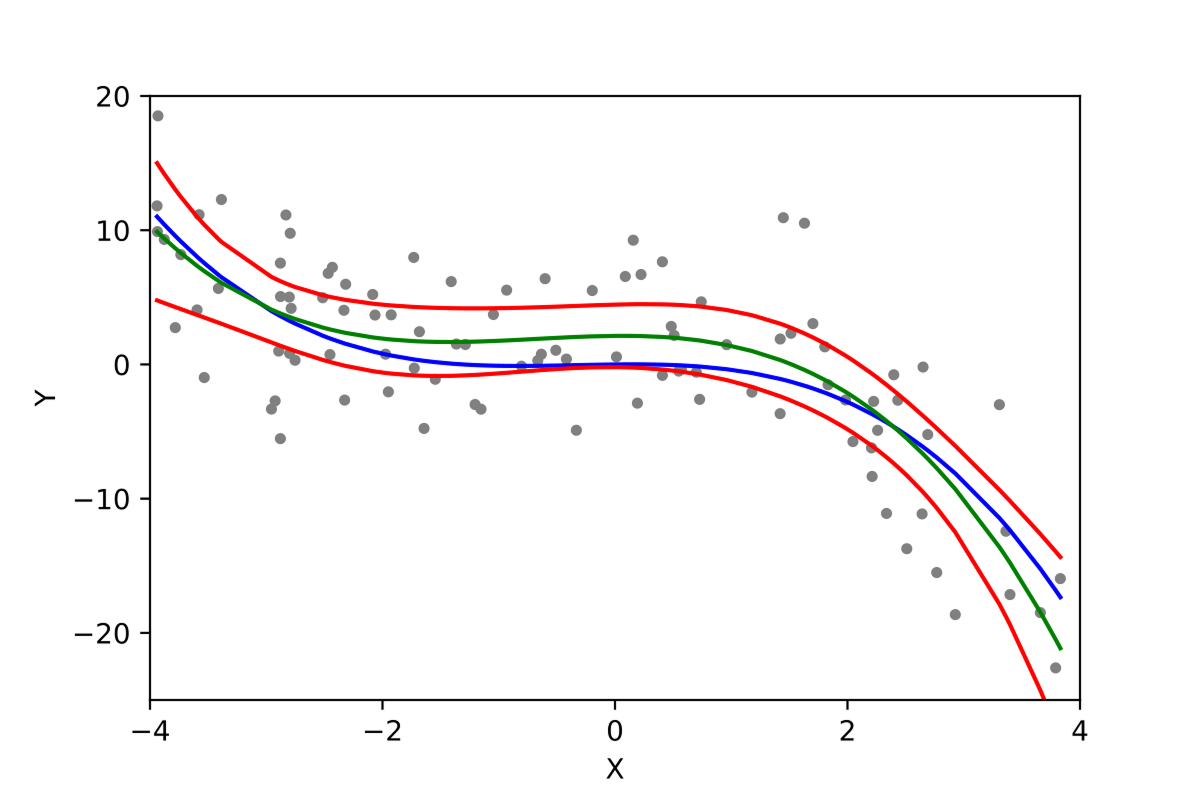
Пример: зависимость урожайности от количества удобрений. Сначала урожайность растёт, но если удобрений слишком много, начинает падать. Полиномиальная регрессия покажет эту кривую.
Гребневый регрессионный анализ
Этот метод хорошо работает, когда у вас много переменных и некоторые из них могут быть не очень важными. Гребневая регрессия будет штрафовать модель за использование слишком больших значений переменных, чтобы упростить её. Штрафовать — значит просто ограничивать рост переменных.
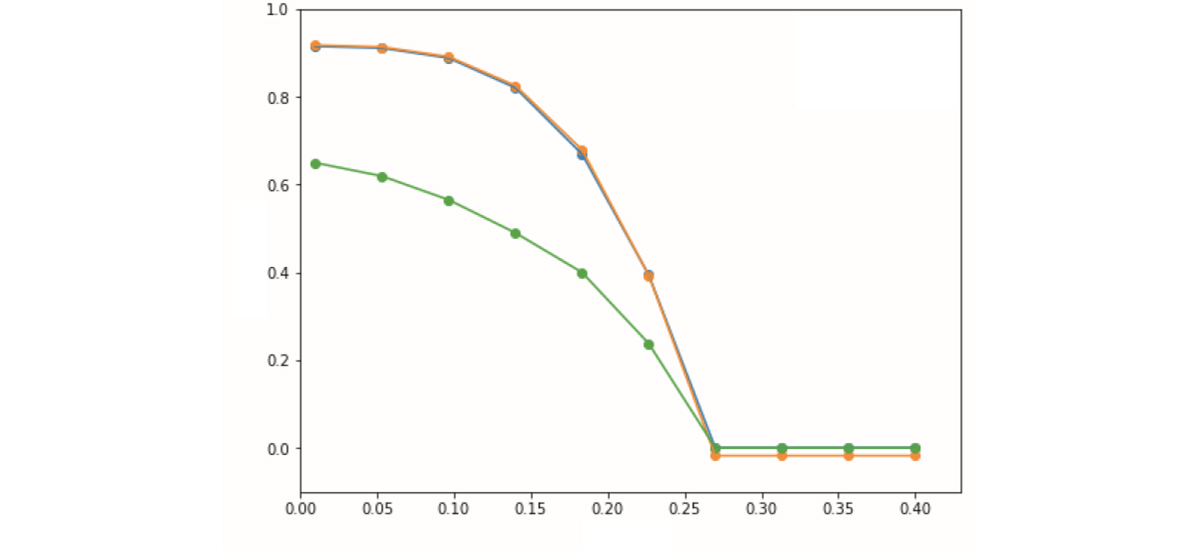
На графике гребневого анализа видно, как некоторые коэффициенты уменьшаются, но не обнуляются совсем. Это потому, что метод использует квадраты коэффициентов, которые могут быть только положительными:
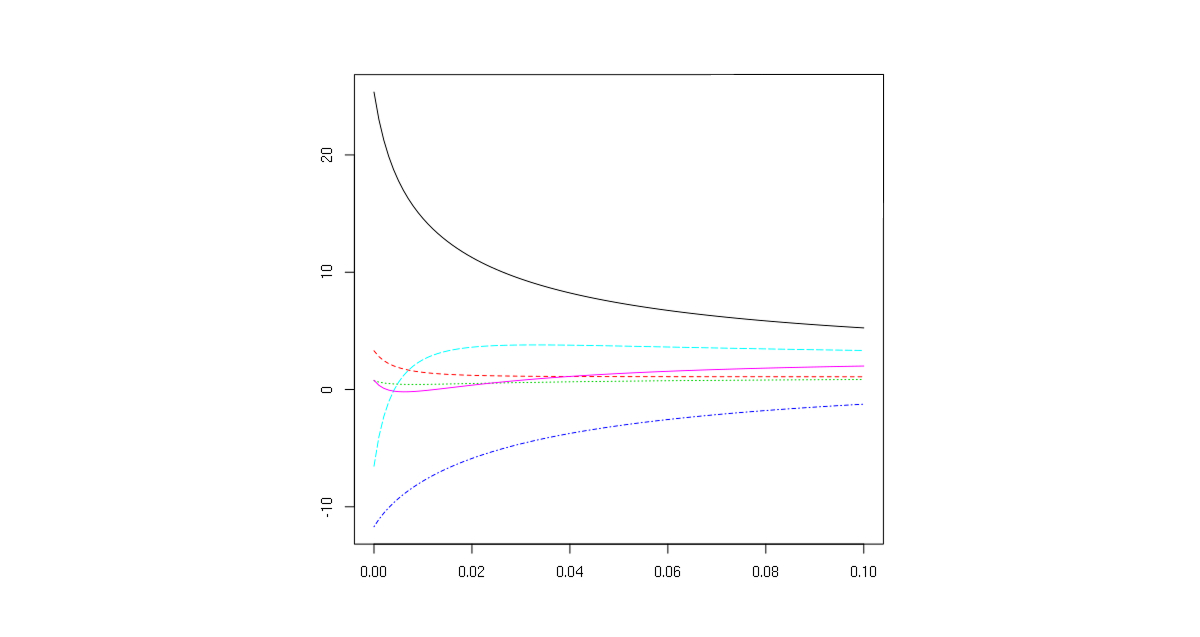
Примером такого метода будет модель прогнозирования цен на недвижимость. На это влияет много факторов: район, количество комнат, год постройки. Влияние части этих факторов можно снизить, если стартовая модель получается слишком уж сложной.
Метод лассо
Похож на гребневую регрессию, но в этом методе некоторые коэффициенты могут обнулиться окончательно. Получается, что метод будет позволять отбрасывать не важные по его мнению коэффициенты.
В примере с ценой дома метод лассо может решить, что год постройки не важен, и полностью исключить эту переменную из модели.
Эластичная сеть
Комбинация гребневой регрессии и метода лассо. Модель одновременно штрафует за сложность модели и отбрасывает неважные переменные.
Графики лассо и эластичной сети похожи:
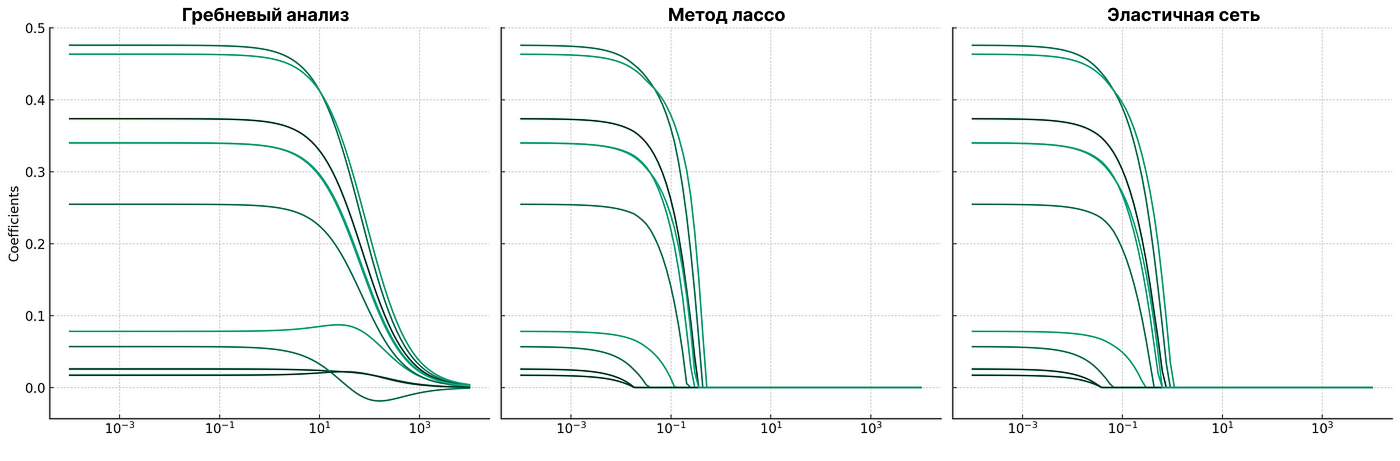
Методы гребневой регрессии, лассо и эластичной сети можно проиллюстрировать на примере укладывания чемодана:
- Гребневая регрессия позволяет укладывать вещи более компактно.
- Метод лассо выкидывает наименее нужные вещи.
- Эластичная сеть совмещает оба подхода: эффективнее укладывает вещи и выбрасывает ненужные.
Этапы проведения регрессионного анализа
Чтобы получить рабочую модель, которая приносит реальные результаты, нужно пройти несколько этапов.
Мы расскажем о них в контексте программирования, потому что наш журнал — про разработку. Но регрессионный анализ можно проводить и вручную с использованием математических формул, если это позволяют задачи и объём данных.
Сбор и подготовка данных. Для анализа нужно подготовить все данные, с которыми будет работать модель. Чаще всего 80% из них пойдут на обучение, а ещё 20% — на финальное тестирование, чтобы убедиться в работоспособности программы. Парето тут ни при чём, это совпадение.
После сбора данных их нужно очистить: удалить случайные, дублирующиеся и пропущенные величины, обработать аномальные показатели.
Очищенные данные нужно привести к одному виду, то есть стандартизировать. Это ускорит работу программы с ними и улучшит финальные результаты.
Построение модели. Чтобы построить модель, нужно выбрать один из методов анализа. После подбора данных с использованием современных фреймворков машинного обучения построить и обучить модель можно за несколько строк кода.
Оценка модели. После готовности модели её нужно протестировать и зафиксировать метрики. Некоторые из них показывают разницу между реальными показателями и теми, что предсказывает программа, другие измеряют скорость работы.
Интерпретация результатов. Это финальная часть, когда аналитики и инженеры выявляют зависимость целевых показателей от независимых. После этого у специалистов должны появиться ответы на вопросы, из-за которых понадобилось провести анализ.
Примеры использования регрессионного анализа
Регрессионный анализ может использоваться в разных областях. Вот четыре примера.
Прогнозирование показателей. Это могут быть показатели продаж на основе уже существующих исторических данных с учётом рекламных расходов, сезонности и других независимых факторов.
Оценка эффективности маркетинга. Можно оценить, как разные маркетинговые каналы влияют на продажи, и сравнить социальные сети, имейл-рассылки, контекстную рекламу и другие площадки. Анализ поможет оптимизировать стратегию.
Оценка риска. Например, банки могут предсказать вероятность банкротства заёмщика на основе его кредитной истории, дохода и других факторов, которые в регрессионном анализе называются независимыми переменными.
Ценообразование активов. Регрессионный анализ помогает определить, как разные факторы влияют на стоимость активов, например акций или недвижимости.
Различия между регрессией и корреляцией
Эти две вещи похожи, потому что обе показывают связь переменных.
Но корреляция только показывает силу и направление связи между переменными и не позволяет строить прогнозы.
- Корреляция: «Чем больше рекламных расходов, тем выше продажи».
- Регрессия: «Если увеличить рекламные расходы на 100 000 рублей в месяц, продажи вырастут на 500 единиц».
Применение регрессионного анализа в Data Science
Прогнозные модели — основной продукт специалистов Data Science. Поэтому регрессивный анализ здорово помогает им в этой задаче и других, например в анализе влияния на целевую переменную и оптимизации бизнес-процессов.