Мы недавно писали о теории игр — разделе математики, который позволяет принимать решения в разных ситуациях. Автор теории игр — математик Джон фон Нейман, и под игрой он понимал любую ситуацию, в которой выполняются такие условия:
- В ней не меньше двух участников.
- У каждого участника свой интерес.
- У каждого участника есть несколько вариантов действий.
- Каждый принимает решения на основании информации о действиях других.
- Есть какие-то общие правила, которые известны всем. Они могут меняться, сокращаться или расширяться, но они быстро становятся известны всем.
С этой точки зрения большинство наших бытовых ситуаций попадает под действие теории игр. Даже обычные переговоры о зарплате или о том, где провести отпуск, — в них тоже действует теория игр.
Одна из самых известных ситуаций в теории игр — дилемма заключённого. В ней нет правильных или неправильных решений, и каждый выбирает сам, что ему делать, но некоторые решения могут сделать ситуацию в итоге лучше или хуже. Про это и поговорим.
Что такое дилемма заключённого
Оригинальная ситуация, с которой всё началось, описывается так:
- Есть два преступника, их поймала полиция в одно и то же время за очень похожие преступления.
- У полиции есть подозрение, что они действовали в сговоре. Чтобы докопаться до сути, преступников развели по разным камерам и сказали им условия.
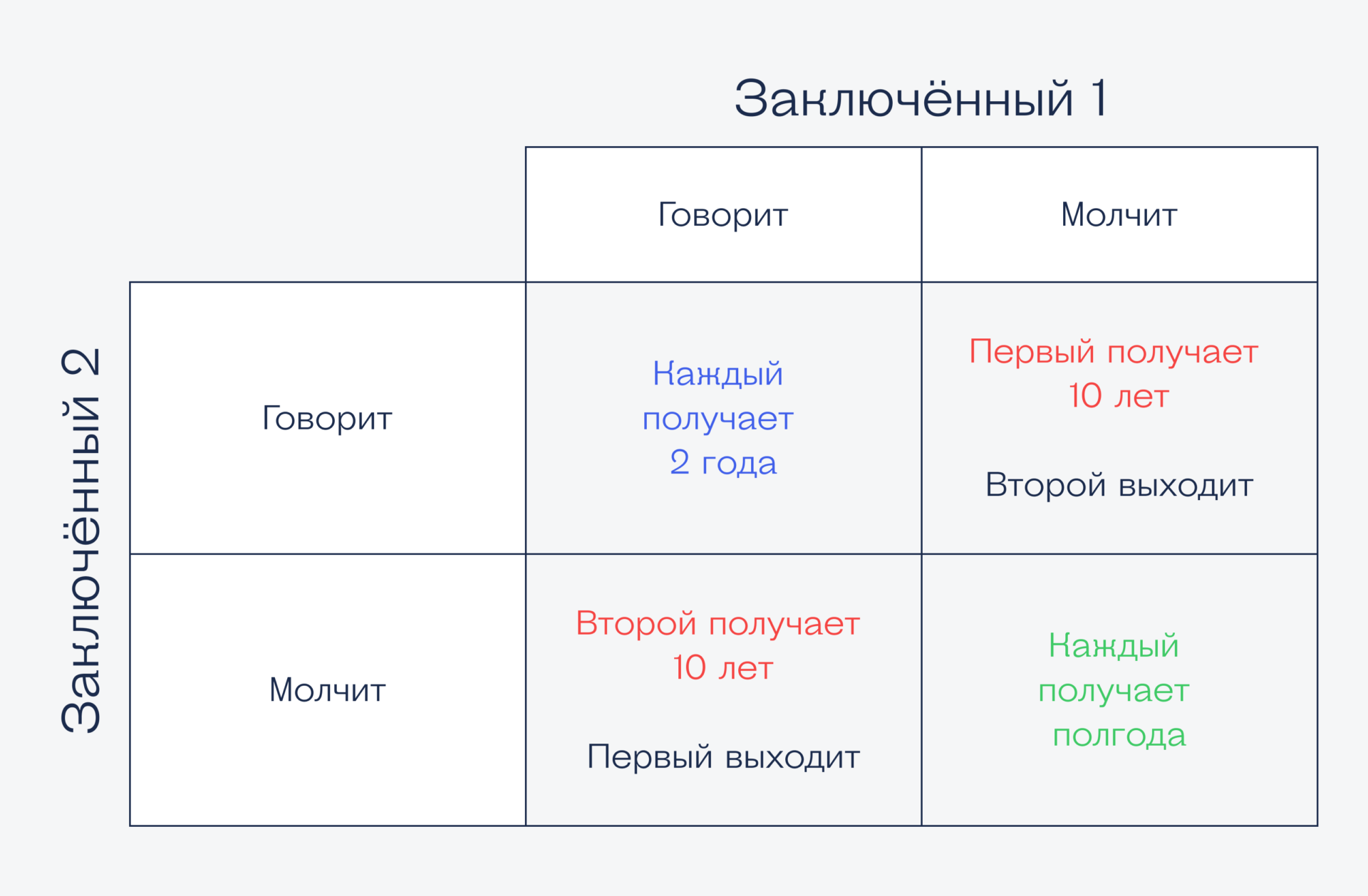
- Если один из них даёт показания на другого, а другой молчит, то тот, кто молчит, получает 10 лет, а первого освобождают.
- Если оба дают показания на другого, то каждый получает по 2 года
- Если оба молчат, то полиция остаётся без доказательств и каждый получает полгода тюрьмы.
- Преступники не могут заранее пообщаться между собой и принять совместное решение, каждый выбирает сам, что ему делать.
👉 Какое решение выгоднее всего принять каждому из них?
Чтобы было понятнее, нарисуем картинку — на ней пересечение решений даст общий результат:
В чём сложность
В дилемме заключённого всё зависит от того, с какой стороны рассматривать эту ситуацию.
Если смотреть с точки зрения заключённого, то его задача — сделать свой срок как можно короче, а в идеальной ситуации выйти вообще без отбывания срока. С этой точки зрения самый плохой вариант — получить 10 лет, когда заключённый молчит, а второй даёт против него показания. Во всех остальных вариантах срок меньше:
- если первый даёт показания и второй тоже их даёт, оба получают по 2 года;
- если первый даёт показания, а второй нет, то первый сразу выходит (идеальная ситуация).
Получается, что, выбрав стратегию «говорить», первый заключённый выйдет на свободу с вероятностью 50% — для него это намного лучше, чем любая вероятность получить 10 лет. Другой заключённый рассуждает так же и тоже выбирает стратегию «говорить». В итоге оба получают по 2 года.
Но если смотреть на эксперимент с точки зрения группы, то ситуация становится совсем другой — чтобы каждый получил минимальный срок, оба должны молчать. Дилемма как раз и заключается в том, что каждый не знает, что выберет другой — идеальный вариант для обоих сразу или только для себя. Если один выберет стратегию «молчать», надеясь, что второй тоже так сделает, то второй может подумать на шаг вперёд и выберет стратегию «говорить» — и выйдет совсем без срока.
Какое решение выбрать
У дилеммы заключённого нет правильного или неправильного решения — всё зависит от того, с какой вероятностью и какой вариант будет приемлемым для каждого участника:
- Если заключённому нужно выйти поскорее любой ценой — он выберет «говорить».
- Если они оба рационально и логически мыслят без влияния эмоций — они выберут «молчать».
- Если заключённому не хочется получить максимальный срок — он выберет «говорить».
В жизни всё ещё сложнее: на выбор влияет дружба, личные отношения, обязательства, внешние факторы и много чего ещё. И простой логикой или математикой тут не справиться — нужно учесть слишком много всего, чтобы принять правильное для себя решение.
Есть ситуации, где можно заранее просчитать риски, вероятности и влияние внешних переменных — в этом случае можно построить математическую модель и рассчитать вероятности успеха при разных стратегиях. Но любая модель — это просто модель, в жизни всё гораздо сложнее.
Где это встречается в жизни
Дилемма заключённого — одна из самых частых ситуаций из теории игр, которая встречается в жизни. Вот некоторые примеры, где ситуация устроена точно так же:
Цены в соседних магазинах. Владельцы могут договориться, слегка повысить вдвоём цены и получить больше прибыли. А может повысить один из них, и если второй не повысит, то при той же посещаемости первый заработает больше, а второй — нет. Ещё может оказаться так, что при повышении цен у первого все пойдут ко второму — это риск, который тоже нужно просчитать.
Бизнес-сделки. Бывает так, что две компании хотят заключить одинаковый контракт с заказчиком. Если оба будут работать сообща, по-партнёрски, то компания разделит контракт пополам и каждый получит одинаковую долю прибыли. Если одна компания будет играть честно, а другая нет (например, подставит компанию-конкурента), то контракт получит та, что будет играть нечестно. А если играть нечестно будут оба, то заказчик, скорее всего, выберет какую-то третью компанию вместо этих двух.
Такие же ситуации есть в экономике, политике, психологии, социологии и в других областях. Можно просчитать некоторые из них и найти оптимальную модель поведения, но чаще всего всё зависит от того, какую стратегию выберет второй игрок.
Что дальше
В следующий раз попробуем написать код, который моделирует дилемму заключённого и предлагает разные решения в зависимости от рисков и начальных условий.