Друзья решили открыть кафе и стали продавать с кофе пончики, рогалики, пиццу и мороженое. Через месяц получилась такая статистика:
- пончики покупают 65% посетителей;
- рогалики — 80%;
- пиццу — 80%;
- мороженое — 90%.
Маркетолог увидел, что как минимум 65% посетителей покупают все эти продукты, и предложил продавать набор из всех четырёх компонентов, чтобы увеличить выручку. Но аналитик сказал, что на самом деле таких покупателей меньше, и доказал это за 5 минут.
Так сколько людей покупают все 4 перекуса?
Чтобы было проще, нарисуем кружочками процентное соотношение всех, кто покупает каждый продукт. Один кружочек — 5%:

Маркетолог думал так: раз 65% покупателей — это минимальное количество среди всех покупателей, то это значит, что эти же 65% точно покупают все 4 продукта:

Но на самом деле это не так. Чтобы выяснить реальное количество таких покупателей, нам нужно рассмотреть самый негативный сценарий — когда покупатели максимально не пересекаются по продуктам.
Начнём с рогаликов: возьмём 20% тех, кто их не покупает и сдвинем влево так, чтобы они закончились ровно под теми кружочками, которые не покупают пончики. Для этого берём этих покупателей…

…и сдвигаем их левее, чтобы они заканчивались там, где заканчиваются покупатели пончиков:

То же самое сделаем с пиццей — передвинем серые кружки левее, чтобы они закончились там, где начинаются серые у рогаликов:

И, наконец, проделаем это с мороженым:

Теперь посмотрим на процент тех, кто гарантированно покупает все 4 продукта — это всего первые три кружка, то есть 15%:

Второй способ решения — использовать круги Эйлера (осторожно, Википедия). С их помощью мы сможем найти пересечения между разными группами покупателей и найти тех, кто берёт все продукты.
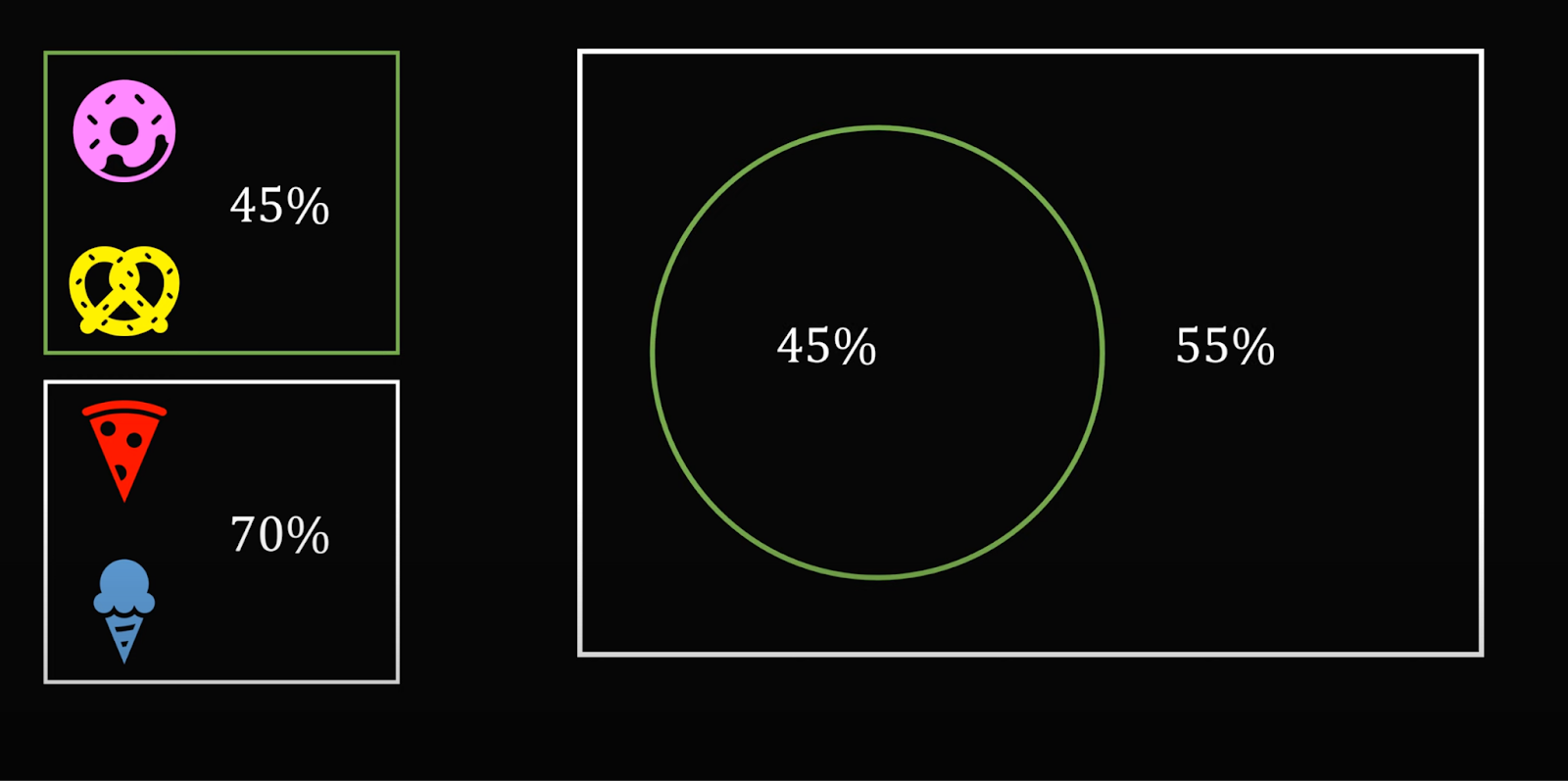
Начнём с пары «пончик — рогалик». Мы знаем, что пончики покупают 65% посетителей — это значит, что 35% их не берут:
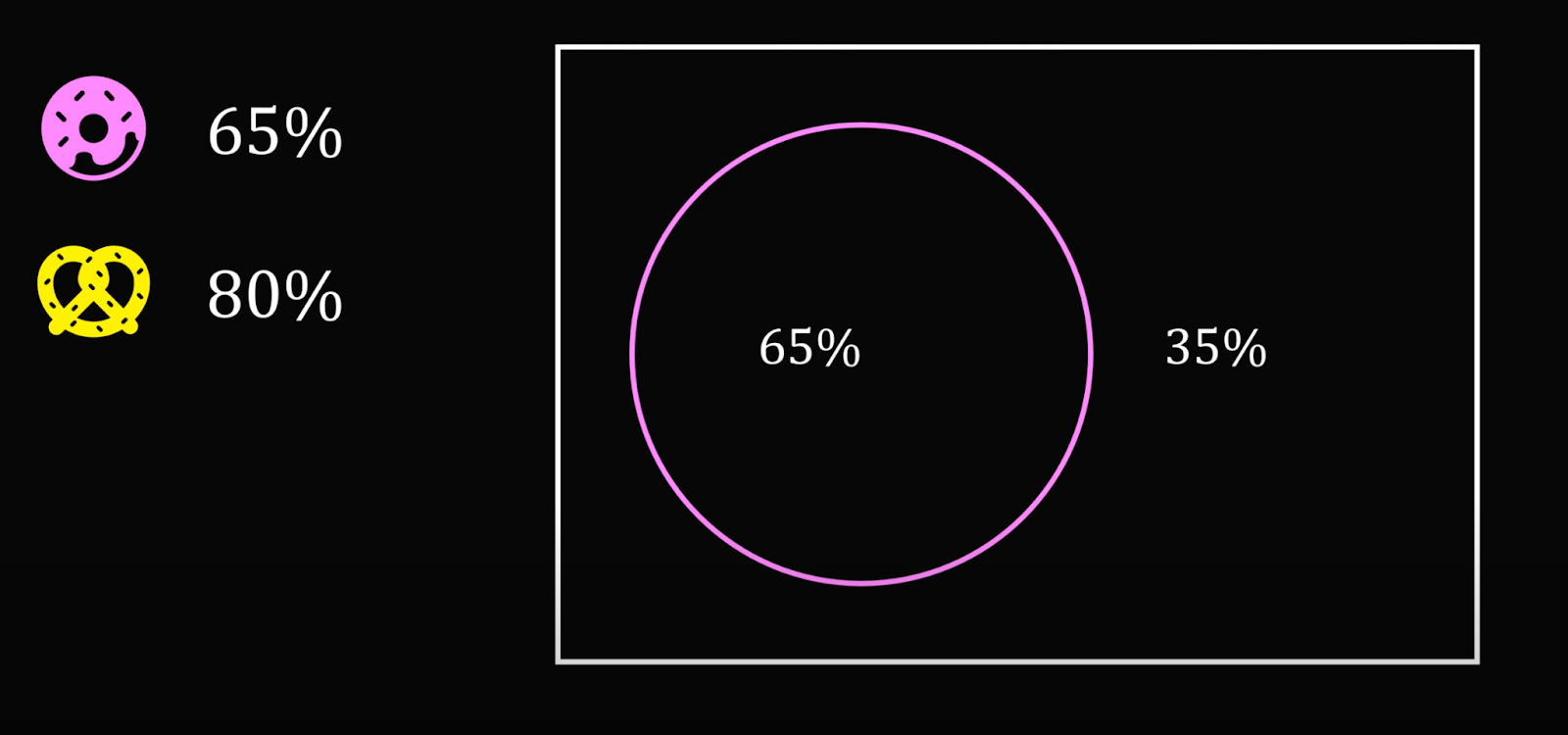
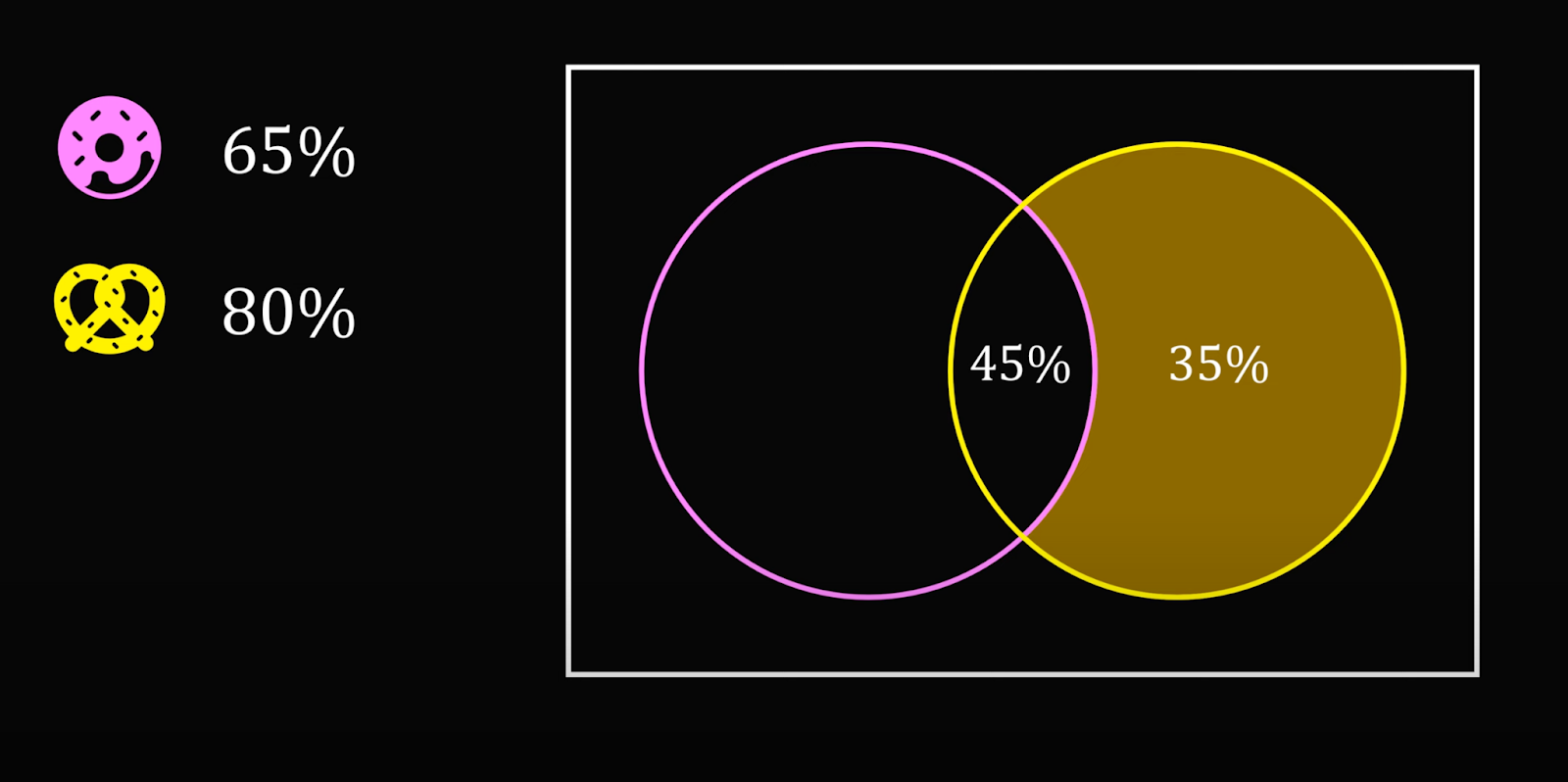
Эти 35% могут также не входить в число тех, кто берёт рогалики, — исходим из этого, чтобы найти минимально возможное пересечение. Получается, что раз 80% посетителей берут рогалики и 35% из них не берут пончики, то в этой паре только 45% посетителей берут и то и другое:
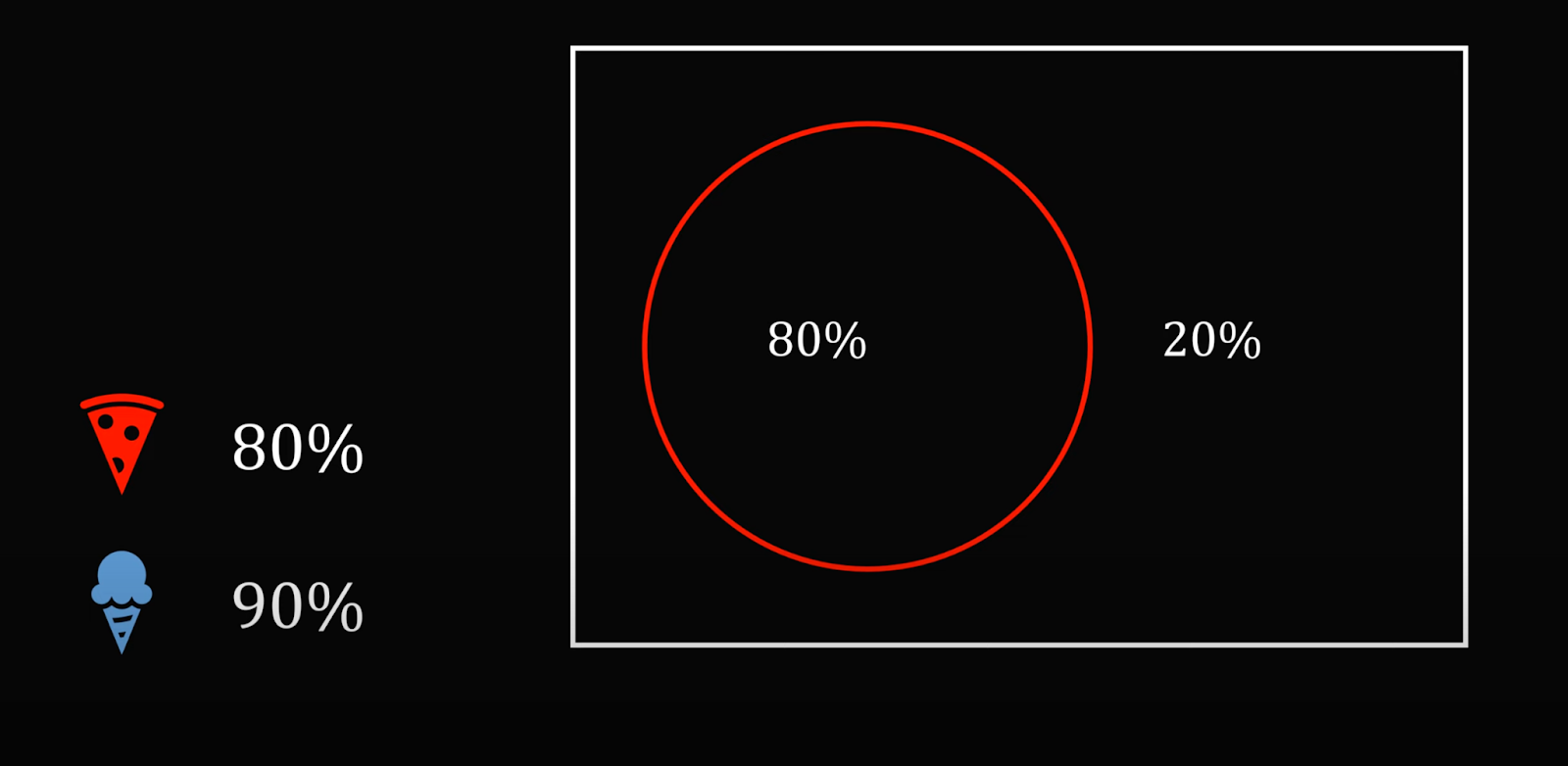
Теперь сделаем то же самое с парой «пицца — мороженое». Если 80% берут пиццу, то 20% её не покупают:
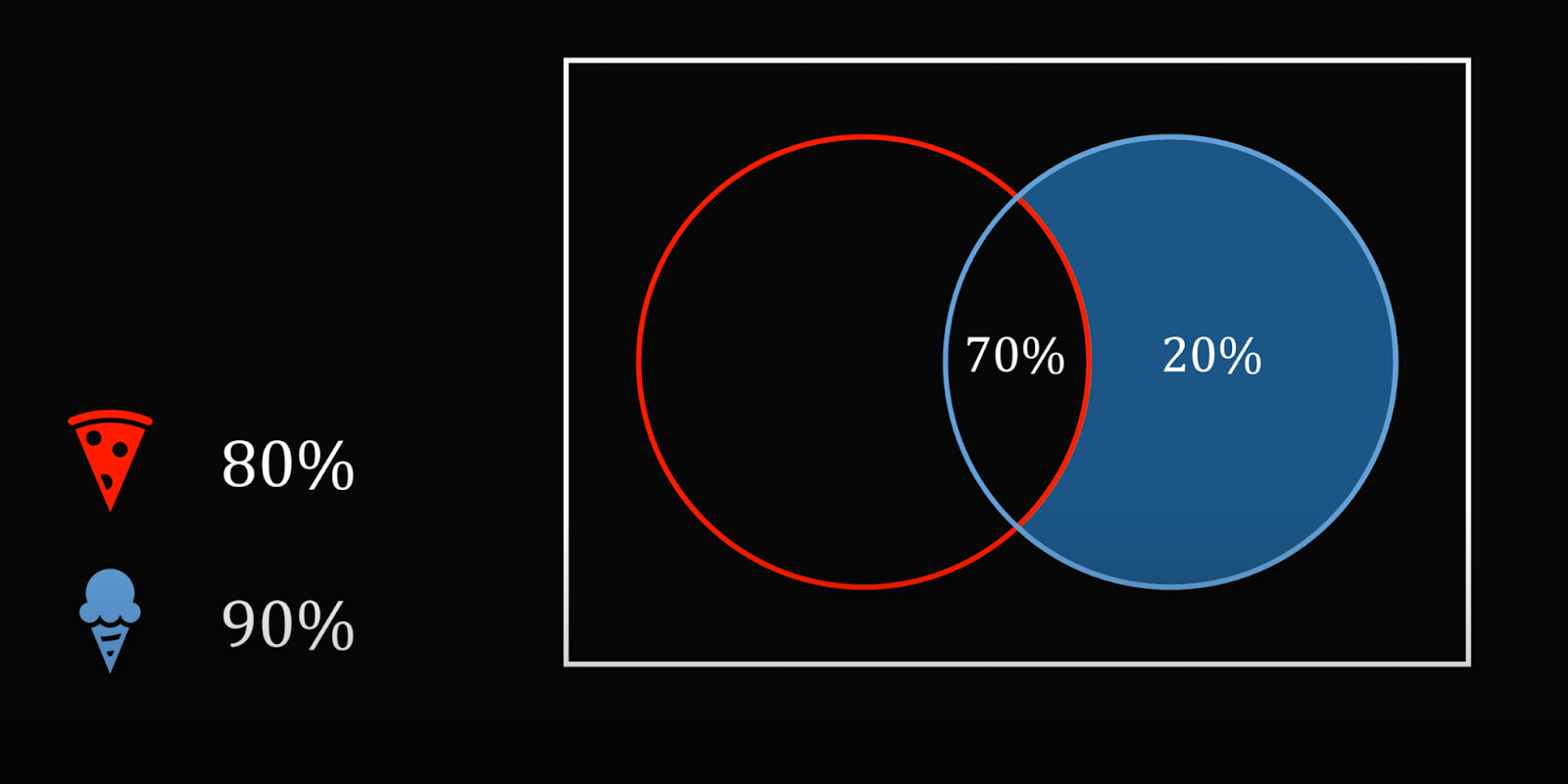
Соответственно, из 90% тех, кто берёт мороженое, 20% не берут пиццу. Значит, тех, кто покупает и пиццу, и мороженое, — 90% − 20% = 70%:
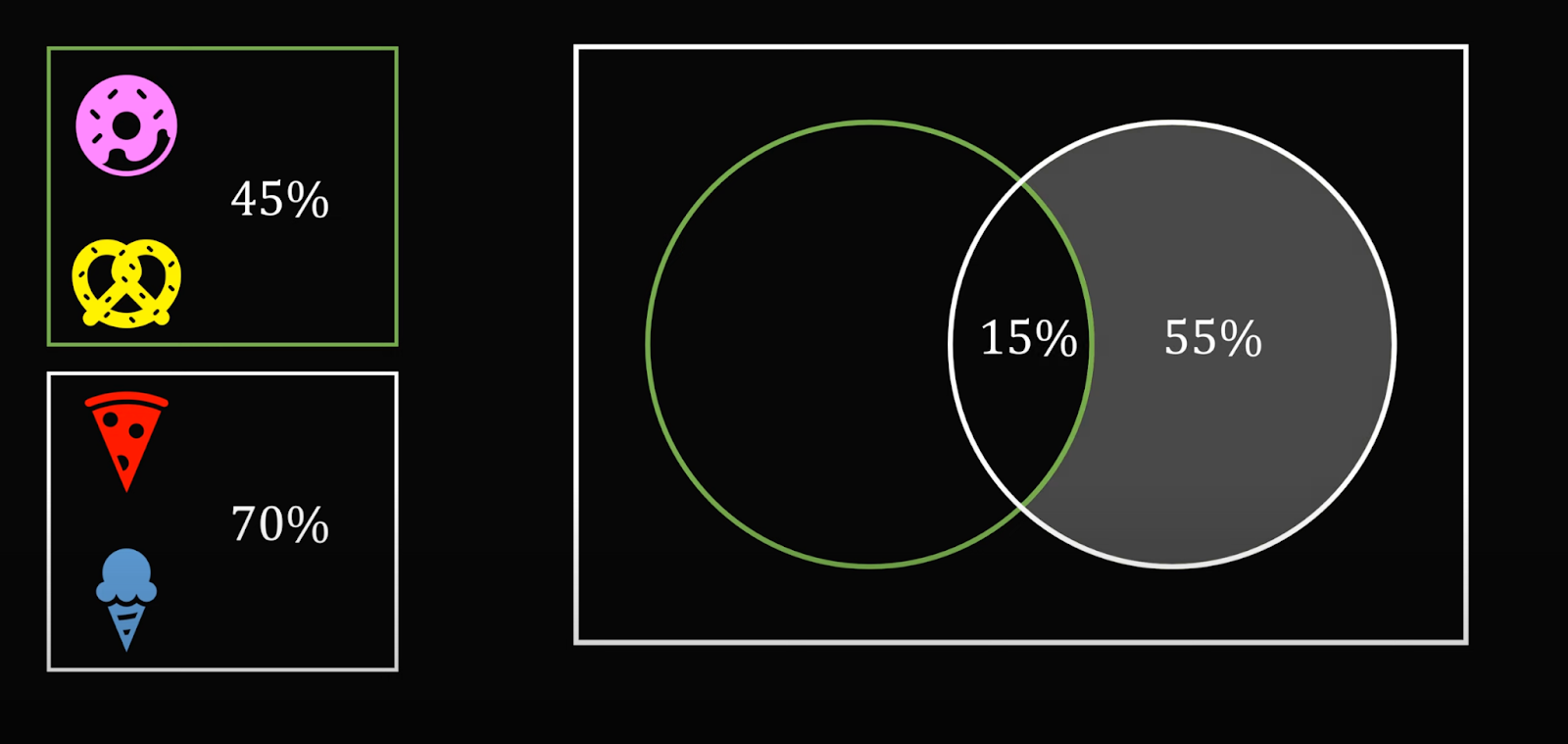
Наконец, объединим эти две группы в одну, чтобы найти общее пересечение — тех, кто покупает все четыре продукта. Для этого сделаем то же самое: если пончик и рогалик берут 45%, то 55% покупателей их не берут:
Добавим сюда тех, кто берёт пиццу и мороженое, — их 70%. А раз 55% не берут пончик и рогалик, получается, что тех, кто берёт все четыре продукта, — 70% − 55% = 15%:
Используем матлогику для решения. Чтобы найти размер пересечения двух множеств, используется такая формула:
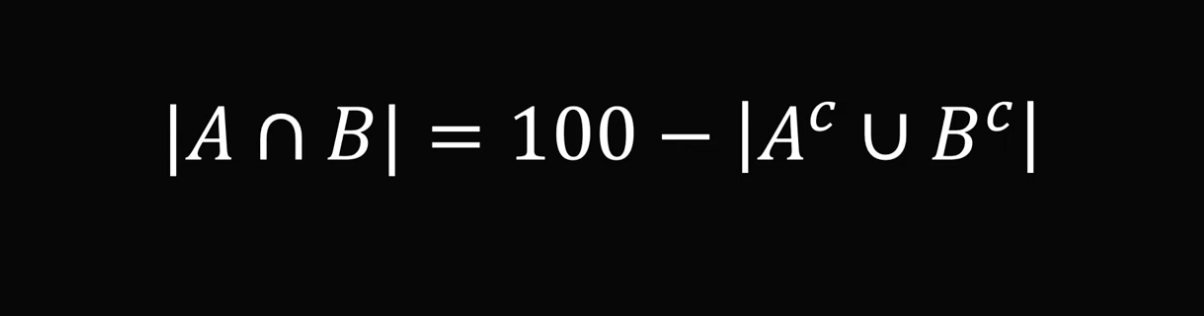
В переводе на русский это значит: чтобы найти процентное пересечение двух множеств, нужно от ста отнять объединение дополнений этих множеств. Дополнение — это то количество, которое не хватает множеству до 100%.
Например, для пересечения пончиков и рогаликов это работает так:
100% − (35% [не хватает пончикам до сотни] + 20% [не хватает рогаликам до сотни]);
100% − 55% = 45% — именно такой результат мы получили в решении с кругами.
Обозначим буквами все продукты:

Теперь используем ту же формулу, чтобы посчитать общее пересечение четырёх множеств:
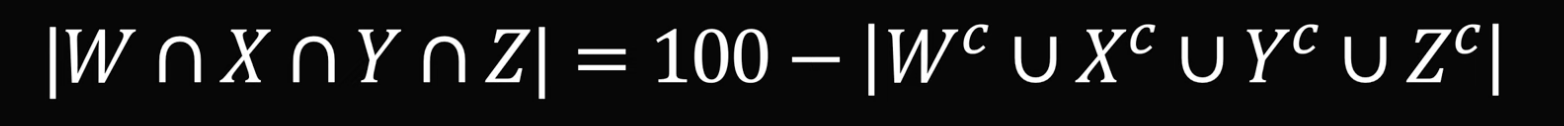
Подставим цифры вместо дополнений и раскроем скобки:
100 − 35 − 20 − 20 − 10 = 15
Получается, что эти множества пересекаются как минимум на 15%, а это значит, что реальных покупателей, которые берут все четыре продукта, — 15%.














