Используйте этот набор задач на вероятности, чтобы проверить себя и друзей. Есть вероятность, что после этого они перестанут быть вашими друзьями.
Футболист против законов математики
Представьте, что вам предложили пари:
- Вы выбираете один из двух вариантов игры с мячом.
- Футболист играет в предложенную вами игру.
- Если футболист выигрывает, вы и футболист получаете деньги. Если нет — никто ничего не получает.
Первый вариант игры — ударить по мячу один раз. Если мяч попадёт в ворота — вы выиграли.
Второй вариант игры — ударить по мячу три раза. Если хотя бы два раза из трёх мяч попал в ворота — вы выиграли.
За выигрыш в любом варианте вам заплатят 50 000 рублей. Какой вариант игры лучше выбрать и почему? Вы знаете, что в среднем футболист забивает три мяча из пяти, но в истории игрока бывало и много непопаданий подряд.
Вероятность
В таких задачах всё зависит от вероятностей — насколько возможно, что это всё произойдёт. Вероятность чаще всего измеряется в процентах: чем они выше, тем вероятнее случится нужное нам событие. Например, когда мы подкидываем монету, вероятность того, что выпадет орёл — 50%. Это значит, что в половине случаев действительно выпадет орёл. А вероятность бросить кубик и сразу получить 6 очков — около 17% или ⅙ , потому что у кубика 6 равноценных граней.
Давайте обозначим символом р вероятность того, что футболист при любом ударе забивает гол в ворота. Получается, в первом варианте наши шансы получить деньги тоже равны р, потому что футболист должен забить с первого раза. Так как вероятность — это число от 0% до 100% (это то же самое, что от 0 до 1), мы имеем два выражения:
р — вероятность, что футболист попадёт в ворота.
(1 — р) — вероятность, что футболист промахнётся.
Если мы выбрали первую игру с одним ударом, вероятность выигрыша равна вероятности попадания в ворота, то есть р. Зная, что футболист попадает три раза из пяти, мы можем смело сказать: вероятность выигрыша в первой игре — 60%. Неплохая вероятность и пока всё очевидно.
А что со второй игрой? Стоит ли пробовать её, если мы знаем вероятность победы в первой? Давайте хотя бы сравним.
Для второго варианта игры есть восемь разных путей развития событий — комбинаций попаданий и непопаданий в ворота. Давайте занесём их в таблицу, и если в какой-то попытке мы попали в ворота — поставим на этом месте галочку. Рядом запишем значения вероятностей этих событий. Вероятности перемножаются:
| Первый удар | Второй | Третий | Вероятность | Выиграли? |
| (1 - p) × (1 - p) × (1 - p) | Нет | |||
| ✓ | (1 - p) × (1 - p) × р | Нет | ||
| ✓ | (1 - p) × p × (1 - p) | Нет | ||
| ✓ | ✓ | (1 - p) × р × р | Да | |
| ✓ | p × (1 - p) × (1 - p) | Нет | ||
| ✓ | ✓ | p × (1 - p) × р | Да | |
| ✓ | ✓ | p × p × (1 - p) | Да | |
| ✓ | ✓ | ✓ | p × p × p | Да |
В таблице приведены все варианты развития событий, никаких других быть не может. Судя по таблице, из восьми вариантов развития событий мы выигрываем в четырёх. Рассмотрим варианты выигрыша.
В трёх выигрышных случаях футболист промахивается один раз. Вероятности у этих трёх сценариев:
(1 — p) × р × р
p × (1 — p) × р
p × p × (1 — p)
Заметили, что все эти формулы можно привести к одному виду?
p × p × (1 — p)
А эта формула, в свою очередь, приводится к такому виду:
p × p × (1 — p)
p² × (1 — p)
p² — p³
В четвёртом призовом случае вы забьёте мяч три раза подряд, и вероятность этого такая:
p × p × p = p³
Чтобы узнать общую вероятность выигрыша, нужно сложить первые три и четвёртую. Для этого достаточно математики седьмого класса. Сделаем это пошагово:
(p² — p³) × 3 + p³
3p² — 3p³ + p³
3p² — 2p³ — это вероятность нашего выигрыша во второй игре.
Мы помним, что вероятность выигрыша в первой игре равна p. Осталось выяснить, что в нашем случае больше: р или 3р² — 2р³. Та игра, где вероятность выше, нам и нужна.
Математическое ожидание
Давайте на секунду забудем, что мы знаем точность нашего футболиста. Мы не в курсе, что он забивает 3 пенальти из 5. Мы лишь знаем, что его вероятность попадания в ворота равна р, при этом если p = 0, мы ничего не выиграем, а если p = 100% (то есть 1), мы точно выиграем 50 000 рублей. Осталось понять, какова вероятность выигрыша в промежуточных сценариях между 0% и 100%. Для этого понадобится математическое ожидание.
Математическое ожидание — это произведение результата на вероятность его получения. В нашем случае — произведение денежного приза на вероятность его получения. Это число не имеет никакого отношения к реальности — по правилам игры при точности футболиста 50% мы не получим 25 000 рублей. Мы считаем математическое ожидание, только чтобы оценить свои шансы.
В первом варианте игры наше математическое ожидание равно 50 000 × р, во втором оно же равно 50 000 × (3р² — 2р³).
Чтобы понять, какое ожидание лучше, давайте нарисуем два графика. Они покажут зависимость результата математического ожидания каждого случая от вероятности того, что футболист забьёт гол. Проще говоря, мы возьмём вероятность гола в 1% и посмотрим, чему будет равно математическое ожидание в обоих случаях. Потом возьмём вероятность 2% и тоже посмотрим на результат ожидания. Потом вероятности 3%, 4%, 5% и так далее. Когда дойдём до 100%, картина будет ясна:
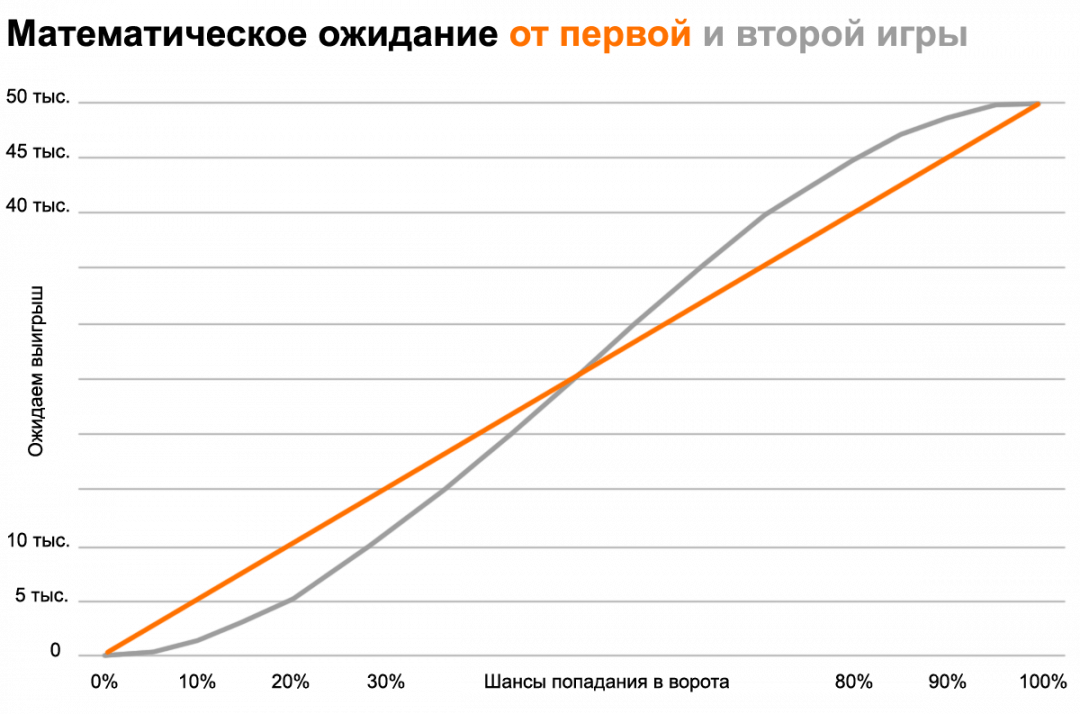
Оранжевая линия показывает график математического ожидания от первого варианта игры. Тут всё понятно: чем точнее футболист бьёт по воротам, тем больше вероятность, что мы выиграем, связь линейная.
Серая линия показывает наши шансы в варианте игры с тремя ударами. Тут начинается самое интересное:
Если точность футболиста меньше 50%, то наше математическое ожидание от второго варианта игры ниже, чем от первого. То есть мазила скорее промахнётся, чем попадёт. И с точки зрения теории вероятностей лучше бы он ударил один раз, чем три.
Если точность футболиста больше 50%, то первая игра даёт более низкое математическое ожидание, чем вторая.
Графики пересекаются ровно посередине, в вероятности 50%. Это значит, что если бы у нашего футболиста всегда было 5 попаданий из десяти, то вероятность выиграть в любой из двух игр у нас одинаковая.
Это можно объяснить ещё и так. Если футболист забивает плохо, то на победу можно не рассчитывать. Максимум, что случится — вам повезёт, и футболист при ударе случайно забьёт гол. Так как такая удача случится, скорее всего, только один раз, то и выбрать в этом случае нужно вариант с одним ударом. А если футболист в целом неплох, то во второй игре у него больше шансов реабилитироваться и отыграться, поэтому нужно ставить на вторую игру.
И финальный штрих: так как мы знаем, что p = 60%, нам очень легко получить математические ожидания от двух игр, зная все вероятности:
Первая игра. Матожидание = 50 000 × 0,6 = 30 000
Вторая игра. Матожидание = 50 000 × (3 × 0,62 — 2 × 0,63) = 32 400
Матожидание от второй игры немного выше, чем от первой. Мы, конечно, не получим этих денег именно в таком виде. Но по этому числу мы видим, что вторая игра с точки зрения вероятностей нам выгоднее.
Рассчитывая вероятности, помните, что вероятность — это не гарантия. В момент игры может подуть сильный ветер, начаться дождь или футболист может быть мотивирован специально мазать мимо ворот (такое сплошь и рядом в теории игр). Вероятности работают только на больших выборках и в строго контролируемых условиях.
Например, нам могут предложить сыграть 100 игр в одинаковых условиях, давая футболисту возможность достаточно отдыхать после каждой игры. Тогда математическое ожидание будет иметь практический смысл.
Но если нам предложат 100 игр подряд на открытом воздухе, после каждой из которых футболист не будет отдыхать, то мы получим как минимум два эффекта:
- футболист будет уставать, его показатель точности со временем снизится;
- за время ста игр может смениться температура воздуха и ветер, что повлияет на точность.
Поэтому математическое ожидание не является гарантией выигрыша. Чем применять матожидание в ставках на спорт или в казино, лучше найти высокооплачиваемую работу программистом.
Морфеус и математика против агентов Матрицы
Однажды агенты Матрицы поймали Морфеуса и дали ему выбирать его же таблетки — красные или синие. Красная возвращает Морфеуса в реальный мир, а синяя навсегда оставляет его внутри Матрицы и в руках агентов. Выбор происходит так: Морфеус сам берёт 50 красных и 50 синих таблеток, как угодно раскладывает их по двум одинаковым коробкам, а потом агент Матрицы сам выбирает любую коробку и не глядя достаёт оттуда случайную таблетку.
Как Морфеусу нужно разложить все таблетки по коробкам, чтобы максимально увеличить свои шансы на возвращение в реальность?
Если сложить все таблетки в одну коробку, то шанс вытянуть красную будет 50/100 или 50%. Такая же вероятность будет, если разложить синие и красные таблетки по коробкам максимально равномерно: 25/50 в каждой коробке. Наша задача — увеличить эту вероятность.
Чтобы это сделать, Морфеус должен в одну коробку положить только одну красную таблетку, а в другую коробку — все остальные таблетки вместе. Теперь посчитаем новые вероятности.
Шанс, что агент выберет коробку, где лежит только одна таблетка, — 50%, потому что коробки одинаковые. А шанс вытянуть красную таблетку, когда в коробке и так только одна красная, — 100%. Получаем, что общая вероятность спасения Морфеуса в этом случае:
0,5 (вероятность выбора коробки) × 1 (вероятность вытянуть красную таблетку) = 0,5, или 50%.
Посчитаем шансы для другого случая. Вторую коробку тоже вытянут с вероятностью 0,5, как и в первом случае. Но вероятность вытянуть одну красную таблетку из 99, где 49 из них тоже красные, равна 49/99 или ~0,495. Перемножаем, чтобы получить общую вероятность спастись в этом случае:
0,5 (вероятность выбора коробки) × 0,495 (вероятность вытянуть красную таблетку) = 0,2475, или 24,75%.
Чтобы узнать общую вероятность на спасение в обоих случаях, складываем вероятности в каждом случае:
Общая вероятность = вероятность в первом случае + вероятность во втором случае.
Общая вероятность = 50% + 24,75% = 74,75%.
Получается, что Морфеусу удалось повысить свои шансы на спасение почти в полтора раза!
Задача про секс и математику
У одного молодого человека было две подруги, они жили в противоположных концах города — на востоке и западе. Парень работал в центре. Каждый день после работы он спускался в метро и садился на первый приходящий поезд. В какую сторону поедет поезд — к той девушке он и отправлялся.
Количество поездов в каждую сторону одинаковое, но парень стал замечать, что в какое бы время он ни выходил с работы, к западной девушке он приезжал в три раза чаще, чем к той, что жила на востоке. Он подумал, что это судьба, и женился на ней.
А действительно ли это судьба или она тут ни при чём? Почему так произошло?
Допустим, у нас поезд отходит каждые две минуты с каждой платформы без перерывов — для чистоты эксперимента допустим также, что у нас круглосуточное метро. А дальше всё дело в интервалах между отправлениями с разных платформ.
Первый поезд на запад у нас будет отходить в начале каждого целого двухминутного отрезка: в 0 минут, 2 минуты, 4 минуты и так далее. Запишем время отправления в минутах и секундах:
0:00
2:00
4:00…
А вот поезд на восток пусть отходит со смещением в 30 секунд относительно западного:
0:30
2:30
4:30…
И там, и там интервал между поездами в одном направлении одинаковый — 2 минуты. Но получается, что после того, как ушёл поезд на запад, у парня есть 30 секунд, чтобы дождаться поезда на восток, если он не успел на первый. А вот потом у него будет целых полторы минуты после отправления восточного, чтобы уехать на запад!
Это значит, что если он каждый раз случайно приходит на станцию, то он должен попасть в 30-секундный интервал, чтобы уехать на восток, или попасть в 90-секундный интервал, чтобы уехать на запад. А раз второй интервал в 3 раза больше первого, то и попадать в него и уезжать на запад парень будет в 3 раза чаще.
Иногда судьба — это простая математика.
Новая должность и выбор зарплаты
Однажды программист устраивался на работу, где ему предложили самому выбрать себе зарплату. Но сделали это хитро, так, чтобы сразу проверить его профпригодность: дали на выбор два конверта.
В каждом конверте лежат листочки с офферами — это документ, где написано предложение с должностью, условиями работы и зарплатой. Два конверта — два оффера. Конверты запечатаны.
В одном оффере денег в два раза больше, чем в другом, но никто не знает, где какая сумма. Программисту можно открыть один конверт, прочитать оффер и решить — оставить этот конверт или выбрать другой. Подскажите программисту, что лучше: оставить этот, выбрать другой или без разницы?
Решение обычного человека
Если рассуждать с позиции простого здравого смысла, решение будет таким: игнорируем эти тупые игры, открываем оба конверта, и если среди них есть здравый оффер — соглашаемся, а нет — до свидания. Ишь чего вздумали!
Можно ещё сказать: «Мне не подходят оба оффера, но если вы готовы предложить мне сумму этих двух офферов, позвоните. Мой номер — произведение первых 10 простых чисел...»
Но можно подойти к решению с точки зрения математики и статистики.
Решение программиста
Чтобы узнать правильный ответ, нам понадобится математическое ожидание — мы уже рассказывали про него выше в задаче про футболиста.
Допустим, что программист выбрал один конверт и обнаружил в нём оффер на Х рублей. Значит, в другом конверте будет оффер либо на 0,5Х рублей, либо на 2Х рублей.
Посчитаем математическое ожидание при выборе того или иного решения. Вероятность нахождения большей или меньшей суммы одинаково и равно 50% или 0,5. Значит, если в конверте лежит 0,5Х рублей, матожидание для него будет равно 0,5Х × 0,5 = 0,25Х. А если там лежит 2Х рублей, то математическое ожидание будет такое: 2Х × 0,5 = Х.
Теперь сложим эти числа, чтобы узнать общее матожидание, если мы выберем другой конверт вместо открытого: 0,25Х + Х = 1,25Х.
В открытом конверте у нас всегда оффер на Х рублей. 1,25X > X, поэтому, с точки зрения математики, выгоднее выбрать второй конверт, так как суммарная вероятность получить больше денег будет выше.
Также важно помнить, что мы говорим о математическом ожидании и статистике: всё это работает на сотнях и тысячах конвертов, если усреднить результат. В отдельном конкретном случае это рассуждение не имеет смысла.
Как выиграть в соревнованиях, когда играешь хуже всех
Андрей, Вова и Сергей участвуют в соревнованиях на мячах, их цель — кинуть мяч так, чтобы попасть в любого соперника. В кого попали — выбывает. Все кидают строго по очереди.
Все знают, что вероятность того, что Андрей попадёт в цель с первого раза, равна 0,3. Вероятность того, что попадёт Сергей — 0,5, а Вова вообще никогда не промахивается, у него вероятность 1,0.
Участники по очереди кидают мяч друг в друга, самостоятельно выбирая цель, до тех поp, пока не останется только один человек.
Как Андрею увеличить свои шансы на победу, если он кидает мяч первым, но делает это хуже всех?
Сначала попытайтесь решить задачу самостоятельно, а если зайдёте в тупик — открывайте решение.
Оптимальное решение — специально кинуть мяч в сторону от всех, чтобы целенаправленно промахнуться. Следите за цифрами.
Если Андрей кидает мяч в Вову, то попадает с вероятностью 0,3 и выиграет, но после этого Сергей кинет в Андрея с вероятностью 0,5. Чтобы Андрей победил, Сергей должен промахнуться, а Андрей в ответ — попасть. Вероятность такого исхода = 0,3 × 0,5 = 0,15. А общая вероятность победить у Андрея с такой стратегией равна:
0,3 × 0,15 = 0,045
Если Андрей кидает первый мяч в Сергея и попадает с той же вероятностью 0,3, то следующим броском Вова попадает в Андрея, потому что никогда не промахивается. В этой ветке событий Андрей проиграл вообще без шансов выиграть. Если же Андрей промахивается, то Вова будет кидать в Сергея (чтобы выбить наиболее сильного соперника), и, как всегда, попадёт. Тогда Андрей следующим броском выбивает Вову с вероятностью 0,3. Считаем общую вероятность выигрыша:
Андрей кидает в Сергея и попадает: шансов на выигрыш — 0.
Или
Андрей кидает в Сергея и промахивается — вероятность 0,7.
Вова кидает в Сергея и попадает — вероятность 1.
Андрей кидает в Вову и попадает — вероятность 0,3.
Вероятность выиграть в таком случае — 0,7 × 1 × 0,3 = 0,21.
Общая вероятность победить по итогам двух вариантов развития: 0 + 0,21 = 0,21.
А вот если Андрей специально промахивается, то события развиваются так (исходя из здравого смысла у остальных соперников).
Вове невыгодно кидать мяч в Андрея, потому что когда он выйдет из игры, Сергей выбьет Вову с вероятностью 0,5. Вове выгоднее кинуть мяч и точно попасть в Сергея, потому что у Андрея вероятность на победу всего 0,3.
Получается, что Вова кидает мяч в Сергея, выбивает его, а затем Андрей кидает в Вову и выигрывает с вероятностью 0,3. Запишем это:
Андрей специально промахивается — вероятность 1.
Вова попадает в Сергея — вероятность 1.
Андрей попадает в Вову — вероятность 0,3.
Общая вероятность события: 1 × 1 × 0,3 = 0,3.
Получается, что максимальные шансы на победу у Андрея только тогда, когда он специально промахнётся. Звучит странно, но цифры есть цифры.