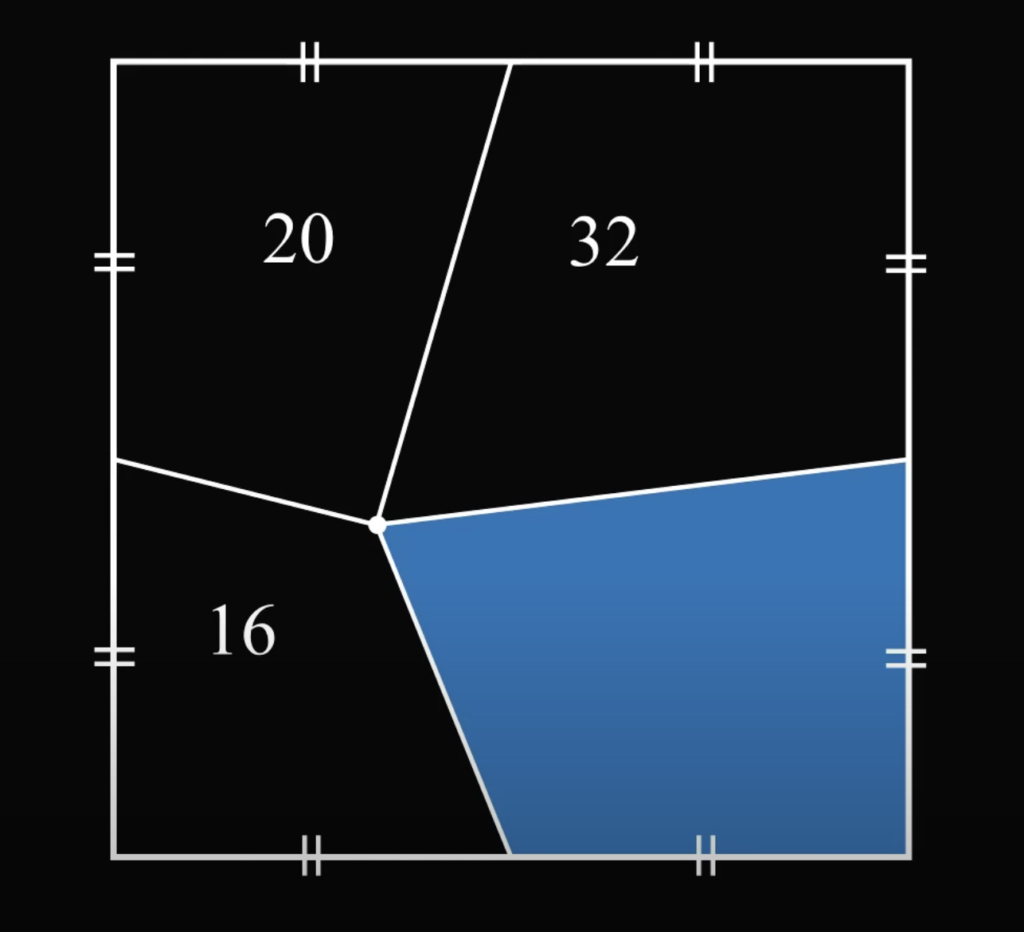
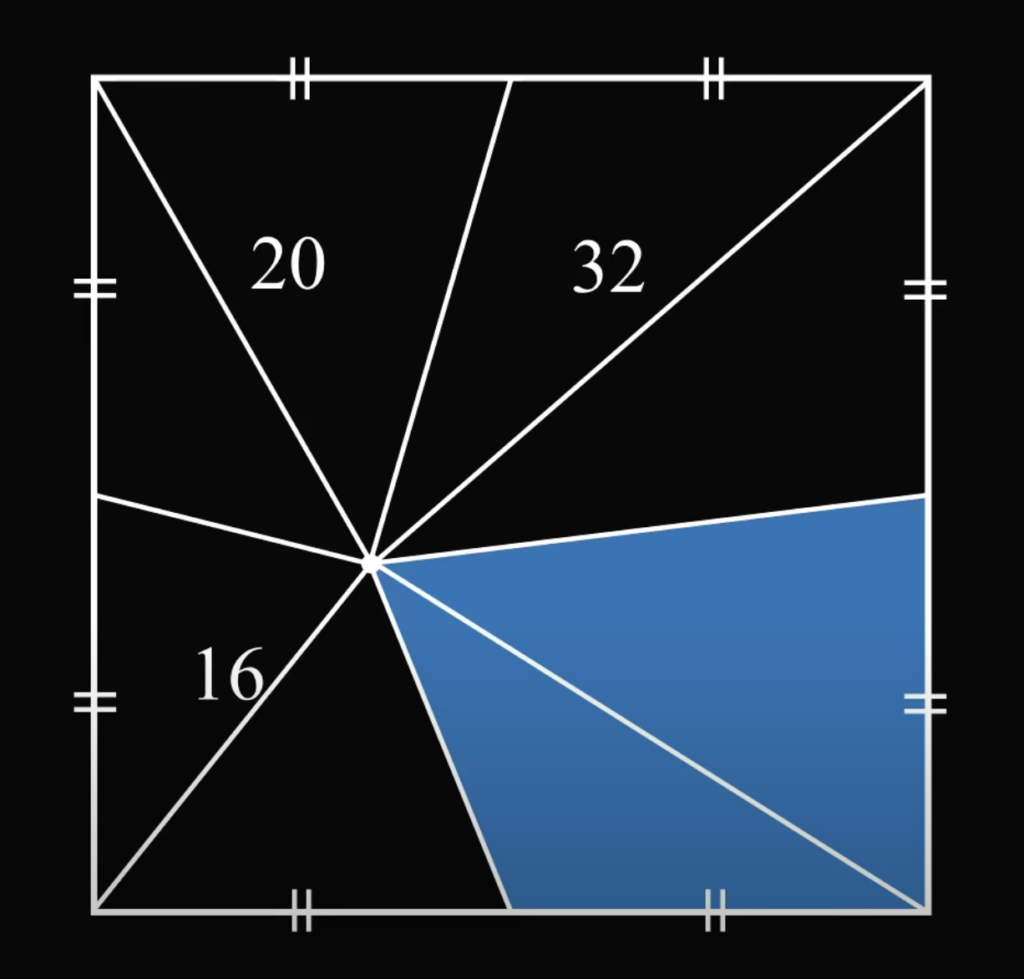
Сразу к делу: есть квадрат, в котором отметили середину каждой стороны. После этого взяли какую-то точку внутри квадрата и провели от неё линии как раз к серединам квадрата, а затем измерили площади получившихся фигур — всех, кроме одной. Как это выглядит и какие там площади — на картинке ниже, а вот вопрос:
какая площадь у оставшейся части?
Если прошло 5 минут, а вы всё ещё не знаете, как подступиться к задаче, загляните в подсказку: возможно, она натолкнёт на нужные мысли.
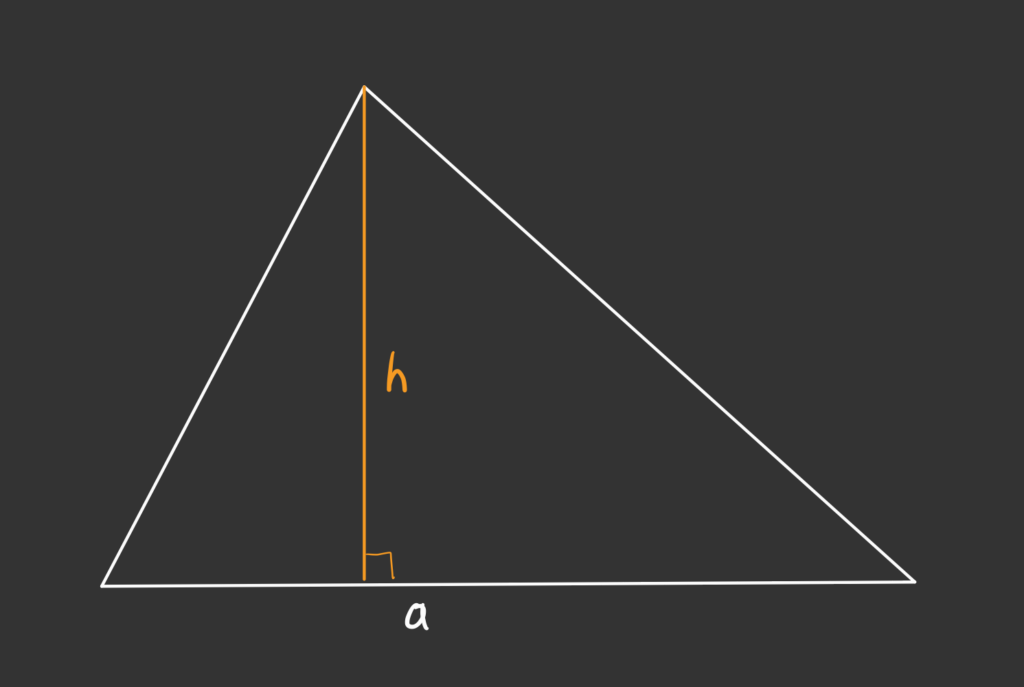
Здесь не будет помощи с решением, но будет про другое: как найти площадь треугольника.
Если что — площадь треугольника равна половине произведения его основания на высоту:
S = ½ (a × h)
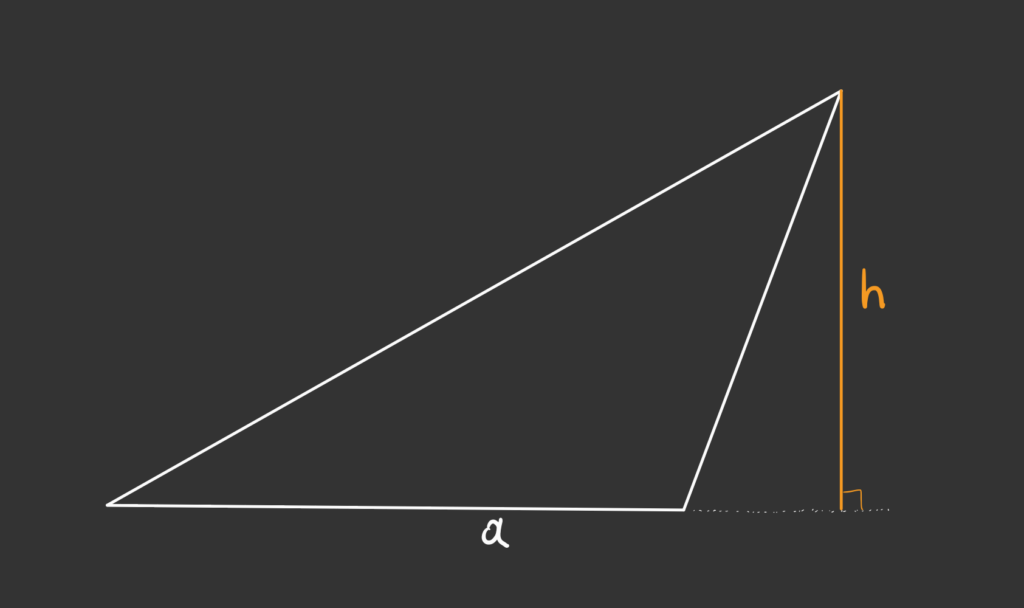
При этом правило работает, даже если высота будет измеряться снаружи треугольника, например как тут:
Если не заглядывали в подсказку — сначала почитайте её, а потом возвращайтесь сюда, знания оттуда нам пригодятся в решении.
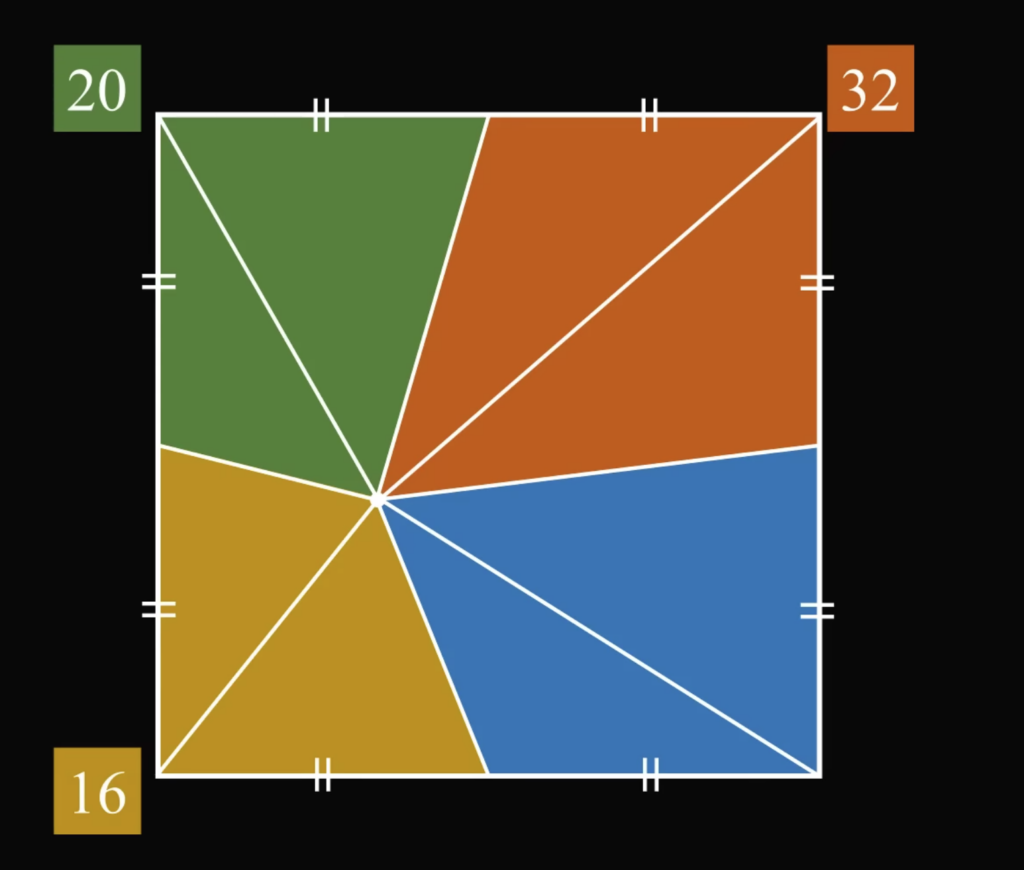
Итак, первое, что мы делаем — проводим до внутренней точки диагонали из углов квадрата, чтобы получилось 8 треугольников:
Затем, чтобы было проще ориентироваться, покрасим изначальные области в разные цвета:
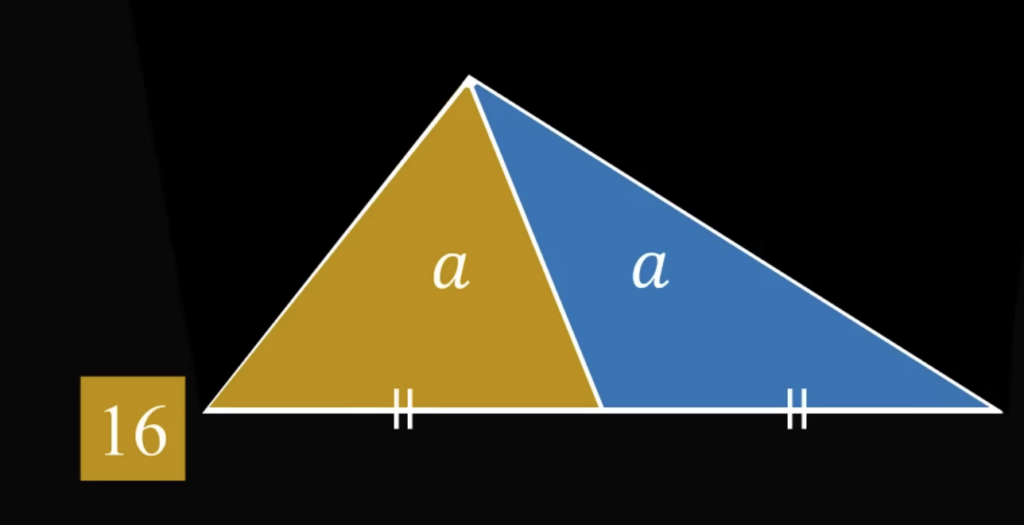
А теперь начинается важная геометрическая магия, следите за руками. Мы берём нижние два треугольника:
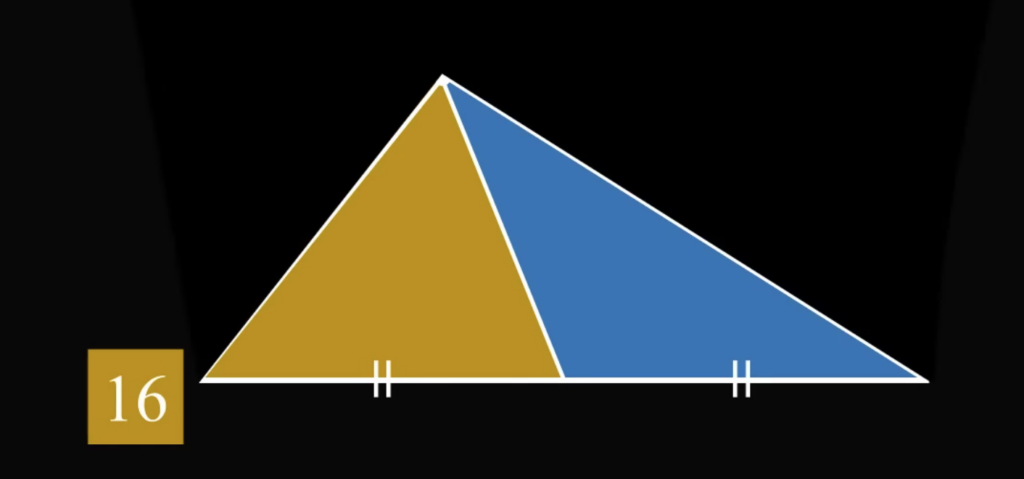
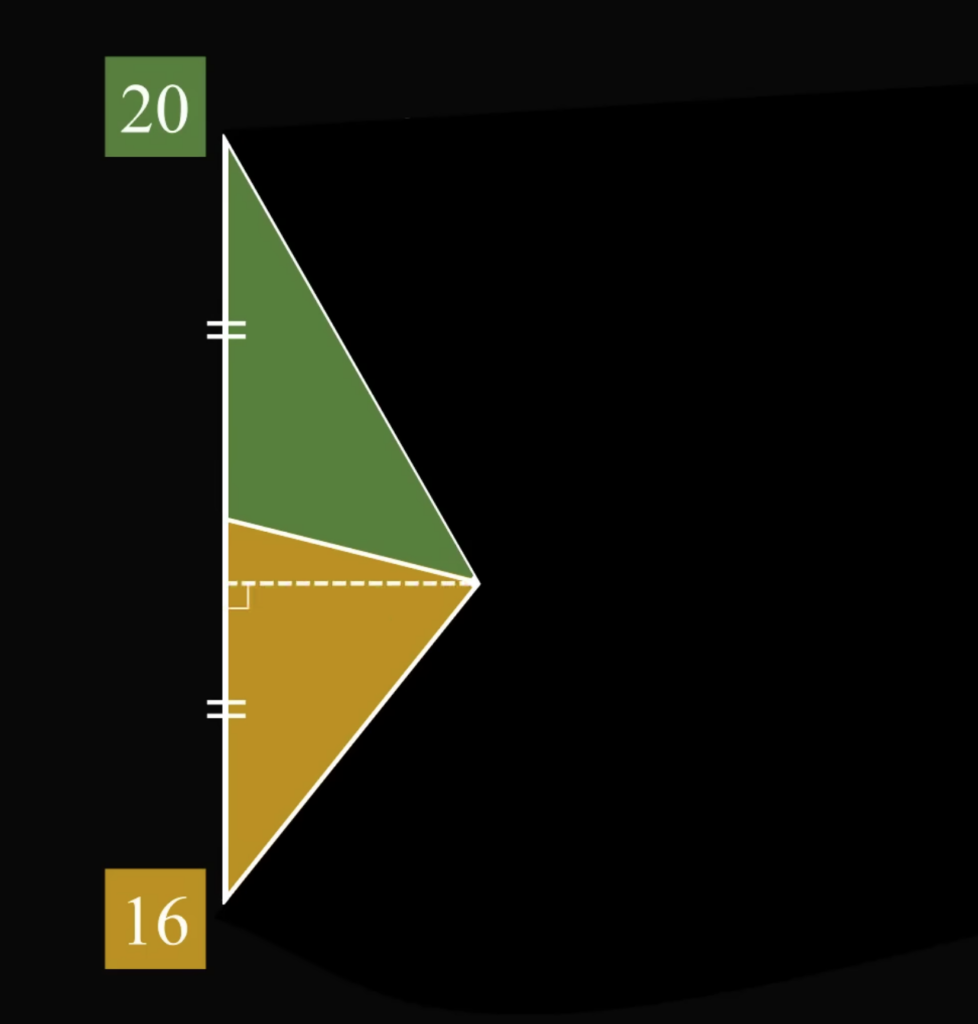
Так как мы проводили первые линии к точке внутри квадрата от середины каждой стороны, то основания этих треугольников будут равны. Но и высота у этих треугольников тоже одинаковая (у одного она получается внутренней, а у другого — внешней):
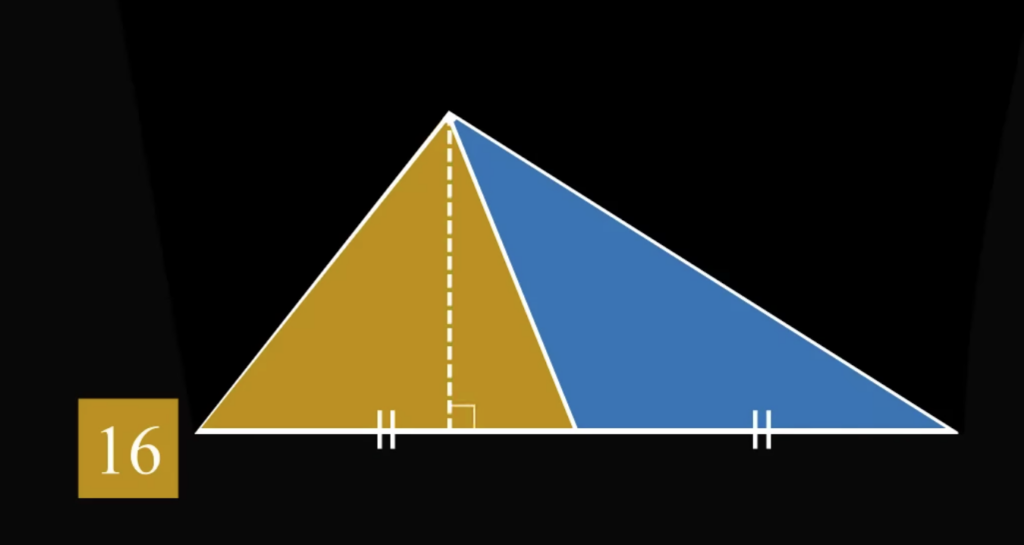
Так как высота и основание у обоих треугольников одинаковые, то и площадь у них тоже будет одинаковая. Обозначим её за a:
Точно так же сделаем со всеми остальными парами треугольников. Покажем на примере левых: у них тоже одинаковое основание и высота, а значит, и площадь тоже одинаковая — обозначим её за b.
Пару итераций спустя получаем такое:
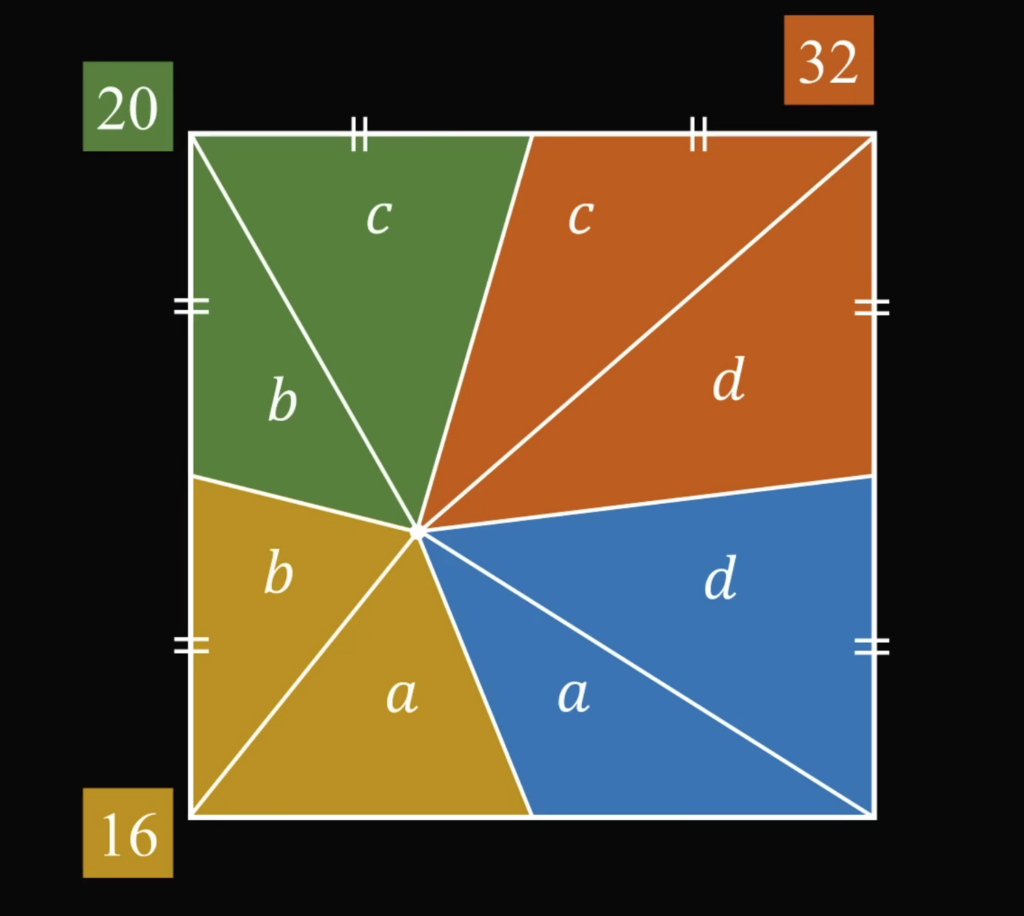
Мы не знаем, чему равны значения a, b, c и d, но мы знаем, чему равна сумма пар разных треугольников — по условию. Например, сумма b и с равна 20. Зная это, составим четыре равенства:
a + b = 16
c + d = 32
b + c = 20
a + d = ❓
Сложим попарно два равенства:
a + b + c + d = 16 + 32
b + c + a + d = 20 + ❓
Теперь смотрите: в обоих случаях у нас получился один и тот же набор переменных, только в разном порядке. А раз так, то можно записать выражение в таком виде:
a + b + c + d = b + c + a + d
Но мы уже знаем, чему равны пары (a + b), (c + d) и (b + c), поэтому заменим их числами:
16 + 32 = 20 + a + d
48 − 20 = a + d
a + d = 28
Это и есть ответ — 28. Если вы его нашли сами — поздравляем, вы крутые!