Сегодня разбираем квантовые компьютеры и основные проблемы, которые они могут создать для обычного шифрования. Это сложная тема, поэтому мы расскажем упрощённо и сокращённо, чтобы читать было интересно и понятно.
Если коротко — квантовые компьютеры уже есть, но пока ничего не изменилось и вряд ли сильно изменится в ближайшие 5–10 лет. Резких скачков в жизни обычного человека точно не произойдёт.
Если хотите длинную версию — читайте дальше.
Что такое квантовый компьютер
Квантовый компьютер нужен для особенных задач и не похож на обычные компьютеры. Выглядит он примерно так:

Нельзя сказать, что квантовый компьютер — это следующий шаг в развитии классических компьютеров. Квантовые технологии работают в миллиарды раз быстрее для одних задач, но остаются на том же уровне или даже бесполезны для других.
Почему так: в обычных компьютерах всё построено на битах, а в квантовых — на кубитах, то есть квантовых битах (от английского q-bit или qubit).
Бит всегда имеет стабильное состояние — 0 или 1. Миллиарды последовательностей нулей и единиц создают работу всех программ, интерфейсов и вообще всего, что происходит внутри машины, и того, что в результате мы видим на экране.
Кубит не имеет чёткого состояния, пока мы его не измерим. Можно сказать, что это как кот Шрёдингера — до измерения состояния он может быть равен как 0, так и 1. А точное значение мы узнаем только в момент измерения. Добро пожаловать в квантовый мир :)
Другой пример — монетка. Если бит всегда будет орлом или решкой, то кубит будет этой монеткой в момент подброса. Мы не знаем, чему он равен, до падения и остановки.
Ещё кубитная логика очень хрупкая. При изготовлении современных кремниевых процессоров легко получить брак от любой вибрации на производстве. Квантовые биты меньше и нестабильнее кремниевых битов во много раз — любой шум или тепловое воздействие оказывает влияние на их состояние.
Из-за такой неопределённости кубиты не приносят пользы во многих простых вещах, которые требуют работы со стабильными долговременными битами или уже оптимизированы. Это, например, обычные арифметические операции, просмотр видео с YouTube или хранение записей в базах данных.
Зато квантовый компьютер может делать то, с чем обычные машины практически не справляются или справляются очень медленно: они умеют моделировать системы и находить правильные ответы, когда нужно работать одновременно с огромным количеством неупорядоченных данных.
Что такое квантовая суперпозиция
Это состояние, когда что-то находится одновременно во всех своих состояниях. Пока кубит не измерили, он находится в суперпозиции — равен и 0, и 1.
Суперпозиция — причина того, почему кубиты умеют делать некоторые вычисления намного быстрее обычных компьютеров.
Пример: у нас есть 4 пары битов в разных комбинациях: 00, 01, 10, 11. Нужно найти пару, которая подходит для решения нашей задачи, например для последнего элемента пароля.
Обычные компьютеры будут искать нужную пару битов обычным перебором, проверяя все варианты по очереди:
00, 01, 10, 11
В квантовых компьютерах все состояния будут проверяться одновременно. В записи это будет выглядеть так:
|ψ⟩ = |00⟩ + |01⟩ + |10⟩ + |11⟩
Что за обозначения:
∣ψ⟩обозначает квантовое состояние суперпозиции, читается как «пси».|00⟩ + |01⟩ + |10⟩ + |11⟩обозначает набор всех возможных состояний пары битов. В реальной записи перед каждым состоянием обычно ставится ещё индекс обозначения вероятности выпадения каждого из них при измерении.
Насколько хорошо нужно в этом разбираться, чтобы понять
Разбираться глубоко нужно только тем, кто серьёзно с этим работает. Всем остальным — в зависимости от интереса и области использования.
Не понимать что-то в математике и физике — это нормально, потому что даже сами математики и физики многого не понимают. А кванты и их взаимодействие — это вообще одна из самых сложных тем. Уравнения в этой области можно решать только приближённо, получить точные результаты не могут даже специалисты и авторы теорий и гипотез. Если не верите — почитайте про сильное ядерное взаимодействие и гипотезу Янга — Миллса, за решение которой вам заплатят миллион долларов в американском математическом институте Клэя.
Аналогия из программирования
В обычном программировании тоже есть технологии и приёмы, которые можно сравнить с обычными и квантовыми компьютерами. Один из таких примеров — синхронное и асинхронное программирование.
Когда процессор обрабатывает тяжёлые математические операции или воспроизводит потоковое видео, он постоянно находится в рабочем состоянии. Это нормально, так и должно быть при работе компьютера.
Но иногда компьютер отправляет запрос в какую-нибудь внешнюю систему, такую как база данных или внешний жёсткий диск. Во время ожидания он может продолжать работать, а может просто ждать ответа и ничего не делать. Тогда получается время простоя.
Если компьютер выполняет все операции последовательно и не использует появившееся свободное время, то управляющая им программа написана синхронным кодом. Если компьютер параллельно с ожиданием ответа от других систем выполняет другие функции, такая программа будет асинхронной.
Как и квантовые компьютеры, асинхронный код может сильно ускорить работу при выполнении определённых задач, но будет бесполезен при использовании там, где уже всё оптимизировано.
В чём суть обычного шифрования
Большинство современных протоколов шифрования основано на принципе P ≠ NP. Это означает, что для сложных задач есть простой и быстрый способ проверки решения, но нет быстрого способа нахождения этого решения.
Пример — кроссворды судоку. Их долго решать, особенно если они большие. Зато проверить правильность решения, можно быстро, это вполне реально сделать даже в уме:
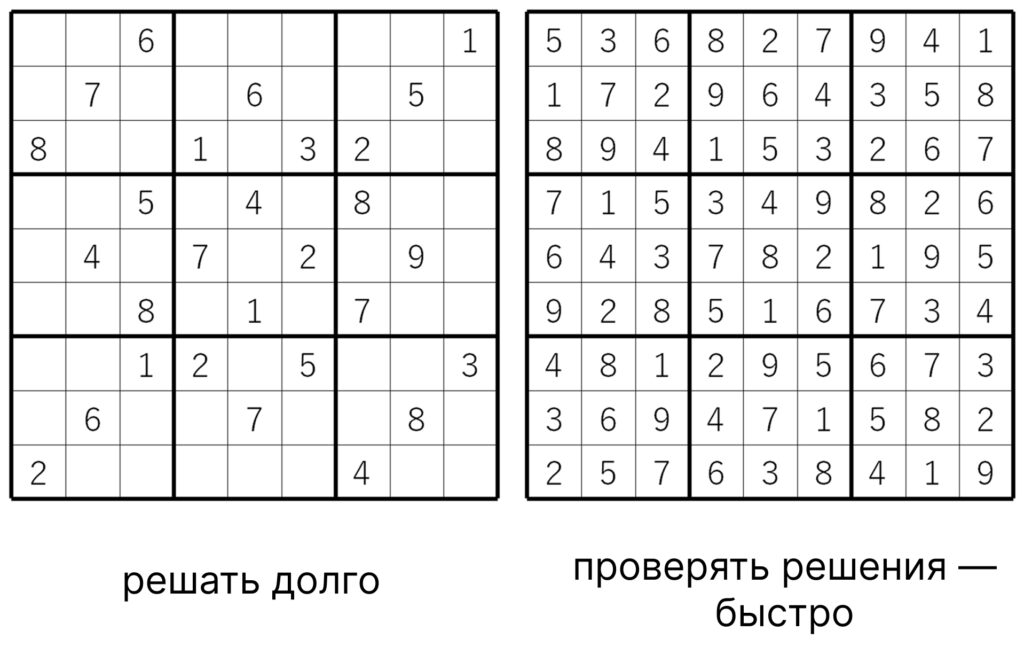
На практике для шифрования чаще всего применяется протокол RSA. В чём его суть:
- Берутся два больших простых числа
АиB(то есть те, что можно разделить без остатка только на 1 и на само себя). - Эти числа перемножаются и получается третье число
C. - Выбирают ещё одно целое число
eтак, чтобы, кроме единицы, у него не было общих делителей, с произведением(A − 1) × (B − 1). - После этого вычисляется
dпо такому правилу: при умножении наeи делении на число(A − 1) × (B − 1)оно даёт остаток 1. - Пара (
e,C) будет публичным ключом, а пара (d,C) — приватным. - Сообщения шифруются публичным ключом, а расшифровываются — приватным.
Почему это надёжно
Чтобы подобрать приватный ключ, нужно вычислить множители большого числа. Это одна из NP-задач — решения можно быстро проверить, но чтобы найти два простых множителя для действительно большого числа, обычным компьютерам понадобятся миллиарды лет.
Есть теория, которая известна как P = NP. Смысл в том, что для всех сложных задач, решения которых можно быстро проверить, есть такой же быстрый способ найти это решение. Это ещё одна из гипотез, за доказательство или опровержение которых положена премия в миллион долларов.
Большинство математиков считают, что эта гипотеза всё-таки неверная и сложные задачи — сложные по-настоящему. Но если вдруг окажется, что нет, придётся искать другой способ шифрования.
Где применяется обычное шифрование
RSA или его модификации используются сегодня почти везде:
- В банковских транзакциях.
- Для цифровых подписей.
- При авторизации пользователей в приложениях.
- Для шифрования сообщений в мессенджерах.
- Во время передачи файлов.
Почему квантовый компьютер может быстро взломать обычные методы шифрования — в теории
Поиск нужного объекта в огромном количестве неупорядоченной информации — это как раз то, что хорошо умеют квантовые компьютеры.
Обычный компьютер будет взламывать шифр RSA методом подбора: подставлять одно значение за другим и проверять, подходят они или нет. Квантовый компьютер будет проверять сразу много значений одновременно, а перед этим сузит область поиска оптимальным способом.
Для нахождения правильных множителей большого числа с использованием суперпозиции кубитов существует алгоритм Шора, который упрощённо работает так:
- У нас есть большое число
C, множители которого нужно найти для взлома шифра. - Мы берём любое число
Xи проверяем, есть ли у него общий множитель с числомC. Почти наверняка такого множителя не будет, иначе получится, что мы раскрыли шифр случайно с первого раза. - Используя неправильную догадку с числом
X, алгоритм Шора может предложить другие два числа, которые с гораздо большей вероятностью окажутся ключами шифра. Для этого берётся за основу такое предположение:X ^ p = 1 (mod C).
На последней формуле остановимся подробнее. У нас есть случайное число X, которое не является множителем конечного большого произведения C. Но для этого числа существует другое число p — и если X возвести в степень p, а потом разделить на C, то мы должны получить в остатке 1.
Если это не так, берём другое случайное число и повторяем процесс. Если так, идём дальше.
У нас есть степень p. Что нужно сделать:
- Возвести
Xв степеньp / 2и вычислить ещё два числа, добавив и отняв единицу. ПолучаемX ^ p / 2 + 1иX ^ p / 2 - 1. - Для каждой пары из этих чисел по отдельности и большого числа
Снужно вычислить наибольший общий делитель (НОД). Для этого есть простой приём, который называется алгоритм Евклида и не требует квантовых вычислений. - С высокой долей вероятности эти два НОД будут нужными ключами-множителями для финального числа
С— а именно это нужно для взлома.
Основная сложность для понимания этого алгоритма в том, что нам нужно найти такую степень p, при возведении в которую число из первоначальной догадки будет подходить к условию: разделив это число в степени p на большое число (множители которого мы ищем), в остатке получим 1.
Обычный компьютер может сделать это только методом перебора, но у квантовых вычислений есть особый приём, в котором скрыта вся магия — это функция Оракула.
Смысл Оракула в том, что он как бы принимает на вход условие, которому должен удовлетворять финальный ответ, а потом проверяет суперпозицию всех возможных ответов одновременно. Он не тратит время на измерения — то есть реальные вычисление и проверку результатов, — а проверяет, насколько близок каждый вариант к правильному. После такой поверхностной проверки мы получаем вероятность, какой из возможных ответов, скорее всего, нам подходит. Это как вероятность значения кубита, который в 33% будет равен 0, а в 67% — 1.
Это звучит непонятно, и объяснение работы Оракула действительно длинное и сложное. Мы расскажем о нём подробнее в отдельной статье, а пока просто запомните:
Квантовые вычисления позволяют находить правильный ответ среди миллионов, глядя на все варианты сразу
Поэтому на то, что обычному компьютеру нужны миллиарды лет, квантовым компьютерам потребуется несколько дней или часов.
Квантовые компьютеры уже существуют и взламывают шифры?
Существуют, но пока современному шифрованию ничего не грозит. Пока что современные технологии не научились создавать квантовые компьютеры достаточной мощности.
Даже в офисах IBM, где квантовые компьютеры хранятся в специальных условиях под температурой около −273° по Цельсию, пока не получается сохранить достаточно долгое время большое количество кубитов — они слишком нестабильные, могут ошибаться, ими сложно управлять. Ещё время жизни кубитов очень короткое, и его не хватает для сложных долгих вычислений, которые потребуются для взлома современного шифра RSA.
Почему, даже если появятся мощные квантовые компьютеры, шифрование никуда не денется
Хотя достаточно мощных для взлома современных шифров квантовых компьютеров пока нет, уже понятно, что современному шифрованию нужно двигаться вперёд и заранее быть готовыми к взлому через алгоритм Шора.
Поэтому во многих современных сервисах и приложениях уже сейчас начинают разрабатывать и внедрять новые методы шифрования. Например, в мессенджере Signal уже сейчас используют протокол шифрования, который называется «Постквантовый Диффи — Хеллманн», и в будущем он должен быть устойчив к кубитам.
Бонус для читателей
Если вам интересно погрузиться в мир ИТ и при этом немного сэкономить, держите наш промокод на курсы Практикума. Он даст вам скидку при оплате, поможет с льготной ипотекой и даст безлимит на маркетплейсах. Ладно, окей, это просто скидка, без остального, но хорошая.