Нерешённые математические задачи, на которых можно заработать

Математикам не дают Нобелевскую премию (по личным причинам), но они могут заработать на задачах тысячелетия. Так называются семь математических проблем, за решение каждой из которых Математический институт Клэя предлагает награду в один миллион долларов США. Одна проблема уже решена, осталось шесть. Сегодня изучим первые три из оставшихся.

Почему назначают награду за решение

Математический институт Клэя в Кембридже не занимается обучением, но поощряет развитие математики. Институт выделяет гранты и премии, а в 2000 году определил семь задач, или гипотез, решив которые, можно значительно продвинуть развитие науки. Решить — значит опровергнуть гипотезу или доказать её или то, что она недоказуема. Словом, получить какой-то однозначный ответ, который поможет математике развиваться дальше. За это и платят.

Расскажите в комментариях, что думаете о такой практике — платить за решение этих задач. Нам действительно интересно.

Что уже решили: гипотеза Пуанкаре

Это задача из топологии — раздела геометрии о свойствах фигур. Вот как она звучит на сложном языке: 

Всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере.

Разберём это утверждение на составляющие:

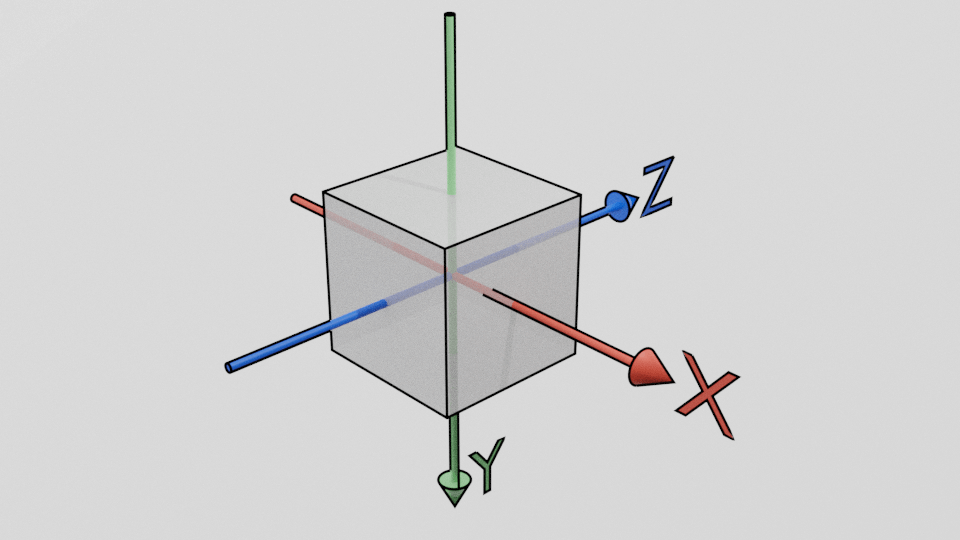
• Трёхмерное многообразие — это любой трёхмерный объект: шар, куб, тор (бублик), кружка, колонна. У этих объектов есть координаты по 3 осям:

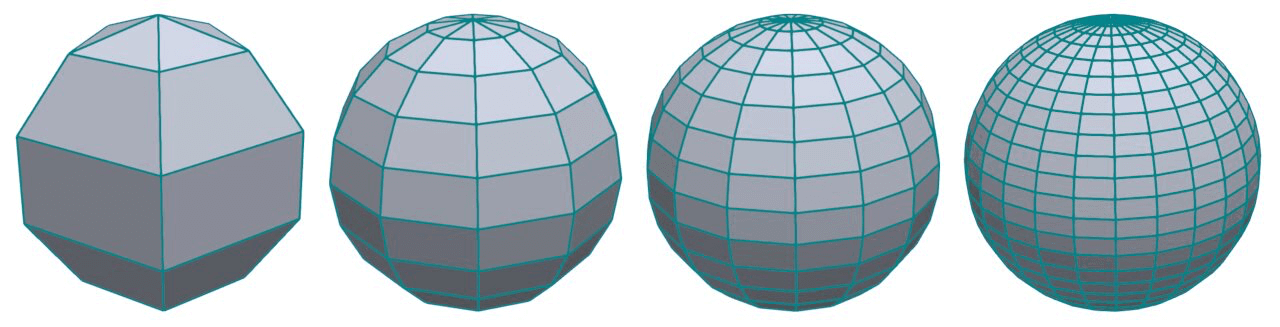
• Односвязность означает, что у объекта нет сквозных отверстий. Например, у сферы, куба и колонны нет отверстия, а у тора и кружки есть. Это можно выразить математически. Для объектов без отверстия всегда верно такое правило:

количество вершин — количество рёбер + количество граней = 2

Правило проверяется для любого объекта, даже сферы, если представить её в виде множества граней:

• Компактность состоит в том, что один объект может поместиться в другой. Например, сфера может быть помещена в куб. Некомпактные пространства тоже бывают, но сейчас мы эту тему затрагивать не будем — и так много сложного.
• Гомеоморфность — это свойство фигур или тел быть «похожими». Иными словами, если представить объект как кусок пластилина, то его можно скомкать и вылепить из него другой объект, не разрезая и не склеивая. Объём и остальное при этом не меняются:

Проще говоря, гипотеза Пуанкаре утверждает, что если у объекта изначально не было отверстия, то из него можно вылепить сферу. А если было — то тор, или бублик. Сложно ли было решить эту задачу? Анри Пуанкаре сформулировал её в 1904 году, а россиянин Григорий Перельман доказал в 2003-м, используя работы другого математика, Ричарда Гамильтона. На решение ушло почти сто лет, а некоторые современные математики говорят, что до сих пор его не понимают.

Равенство классов P и NP

Эта гипотеза — про алгоритмы. На всякий случай напомним, что алгоритм — это последовательность действий, которая приводит к нужному результату. 

Для понимания задачи равенства P и NP нужно понять, почему одни алгоритмы сложнее других. Сложность алгоритма — это зависимость скорости поиска решения от количества входных данных. Если с увеличением таких данных скорость поиска решения растёт не очень быстро, такие алгоритмы называются простыми. А если скорость увеличивается резко — это сложные алгоритмы.

Например, в задаче 128 элементов. Если к ней можно применить алгоритм со сложностью log2n, то log2128 = 7, то есть результат будет получен за 7 действий. А если взять алгоритм со сложностью факториала n!, то для решения понадобится такое количество действий:

385620482362580421735677065923463640617493109590223590278828403276373402575165543560686168588507361534030051833058916347592172932262498857766114955245039357760034644709279247692495585280000000000000000000000000000000

Так выглядит таблица, где зелёным цветом выделены простые алгоритмы, а красным — сложные:

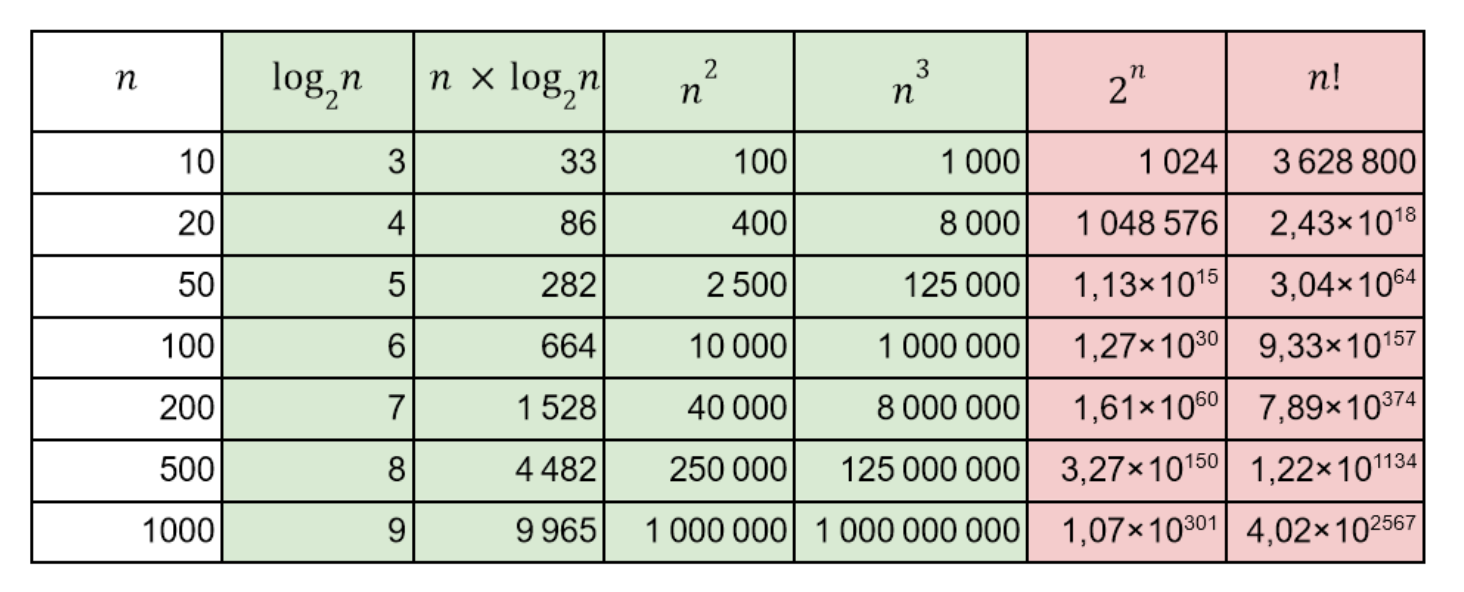
Для всех простых алгоритмов количество действий для решения можно задать формулой через многочлен, или полином. Например, через такой: 

10n² + 20n + 30 = количество действий для решения

Здесь мы увеличиваем количество входных данных n, и сложность растёт по формуле полинома. Если задачу можно решить алгоритмом такого вида, она называется полиномиальной, или задачей класса P.

Для второго класса задач сложность растёт намного быстрее. Пример такой задачи — кроссворды судоку. Чем больше столбцов и строк в таблице с числами, тем сложнее решить кроссворд. Простого способа решения для них нет — по крайней мере, оно неизвестно.

При этом проверить решение можно довольно быстро, поэтому говорят, что решение проверяется за полиномиальное время. Такие задачи называются недетерминированными полиномиальными, или задачами класса NP: за P-время можно проверить решение, но неизвестно, можно ли его найти.

Класс NP включает в себя класс P, потому что все P-задачи можно проверить за P-время. 

Для доказательства гипотезы нужно доказать и обратное:

Все задачи класса NP равны задачам класса P

Если это предположение правильное, то для любой NP-задачи — даже для судоку с миллионом полей — есть простой алгоритм решения.

Осталось разобрать ещё одно: NP-полные задачи. Это задачи, к которым сводится любая задача класса NP. Поэтому, если вы найдёте простой алгоритм для одной из NP-полных задач (осторожно, Википедия) — решите все и получите миллион долларов. Например, задача о рюкзаке: как уложить как можно больше ценных вещей в рюкзак при условии, что вместимость рюкзака ограничена?

Если однажды окажется, что NP-задачи можно решить каким-то простым алгоритмом за полиномиальное время, это разрушит всю конфиденциальность: банковские счета, аккаунты в интернете и всё, что защищено шифрованием. Это потому, что большинство алгоритмов шифрования — тоже NP-задачи. Разгадывать их долго, а проверять просто. Но скорее всего, волноваться об этом не стоит. Большинство математиков говорят, что сложные задачи на самом деле сложные, и простых решений для них нет.

Гипотеза Ходжа

Эта задача алгебраической геометрии сформулирована в 1941 году Уильямом Ходжем. Алгебраическое уравнение — это математическое равенство с многочленами. К ним относятся линейные и квадратные уравнения, которые мы решали в школе, например x + 3 = 5. 

У уравнения есть степень — это количество элементов. Уравнение 7-й степени может выглядеть так:

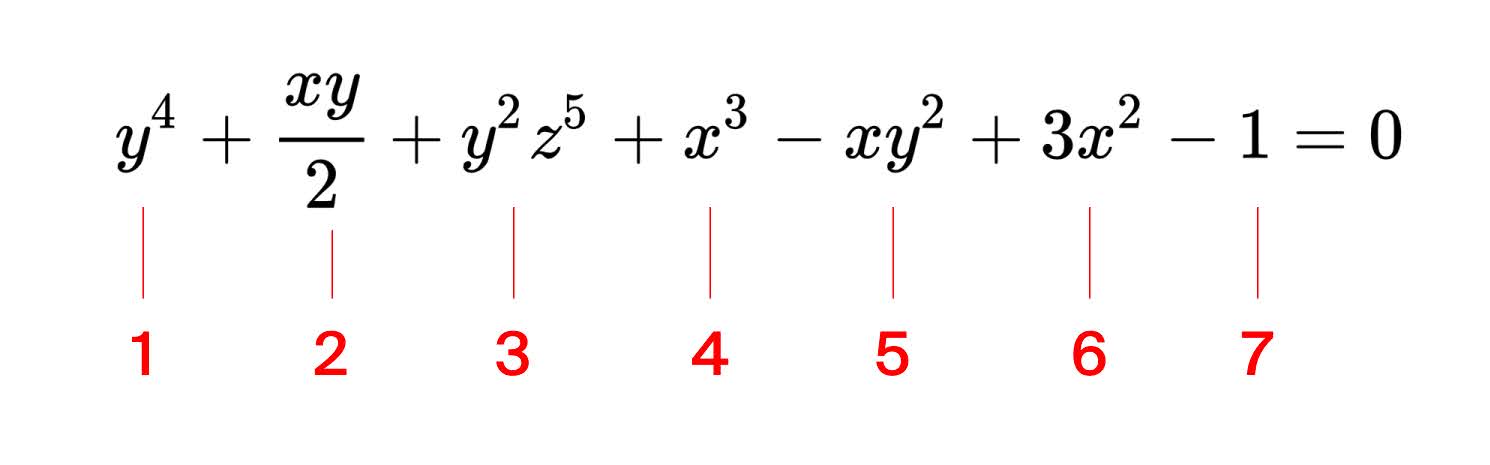
Ещё можно сказать, что это алгебраическое уравнение 7-й степени от 3 переменных: x, y, z. У такого уравнения может быть не одно решение, а множество. Например, для уравнения x + y = 10 будет бесконечное множество решений.

Множествами решений уравнений можно описывать фигуры. Вот уравнение для сферы:

(x – a)² + (y – b)² = r²

Алгебраическая геометрия изучает геометрические фигуры, которые можно задать множеством решений алгебраического уравнения. Такие фигуры называются алгебраическими многообразиями. Пример алгебраического многообразия — поверхность Тольятти, которая задана уравнением 5-й степени:

Если объект слишком сложен, форму и её уравнение можно разбить на несколько и изучать их по отдельности. Ходж предположил, что для отдельного типа алгебраических многообразий, которые называются проективными, это верно всегда. Заумным языком гипотеза Ходжа звучит так:

Для проективных алгебраических многообразий циклы Ходжа являются комбинациями алгебраических циклов

Для доказательства или опровержения нужно выяснить, до какой степени можно разбивать формы объектов и их уравнения, чтобы эти фрагменты соответствовали общей сложной форме? Некоторые математики считают, что сегодня решить эту задачу невозможно: необходимо более подробно изучить саму алгебраическую геометрию.

Гипотеза Римана

Это теория о простых числах. Давайте вспомним:

Но чтобы понять, о чём речь, нужно разобрать ещё два вида чисел: мнимые и комплéксные.

Мнимые числа обозначаются в формулах буквой i и существуют только как абстракции. Обычно говорят про конкретное число — мнимую единицу, которая обозначается буквой i и квадратный корень которой равен -1. Если видите в формуле i2— знайте, что это отрицательная единица:

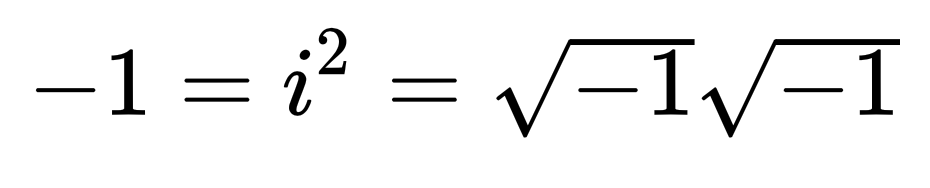
Комплéксные числа обычно обозначают буквой z. Они состоят из двух обычных действительных чисел a и b и одного мнимого и выглядят так:

z = a + bi

Часть a называют вещественной, а bi — мнимой. Если b будет равно 0, то всё комплéксное число равно вещественной части a.

Ни мнимые, ни комплéксные числа нельзя хоть как-то изобразить для более простого понимания. Это то же самое, что пытаться показать четырёхмерный мир.

Теперь попытаемся понять, как это всё связано с простыми числами. Проблема в том, что до сих пор неясно, по какому правилу они встречаются, если считать от единицы до бесконечности. Кажется, что никакой закономерности нет:

Функцию для описания появления простых чисел называют пи-функцией и обозначают как π(x). Единого описания пи-функции нет. Можно только построить её график для любого отрезка натуральных чисел, например от 1 до 60:

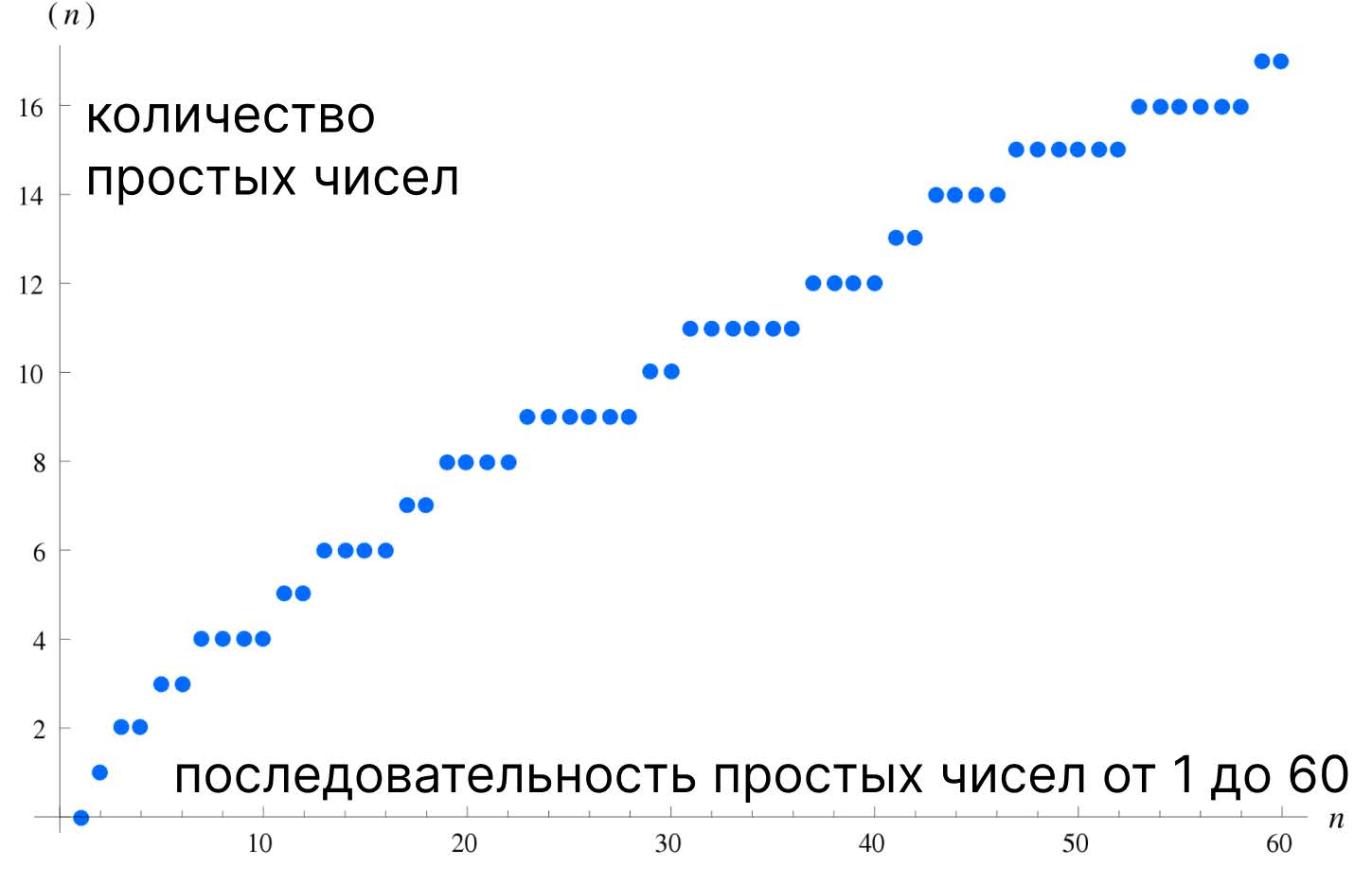
Математик Бернхард Риман заметил сходство распределения простых чисел на пи-функции и функции, которую сегодня называют дзета-функцией Римана. Её обозначают строчной буквой ζ, и выглядит она так: 

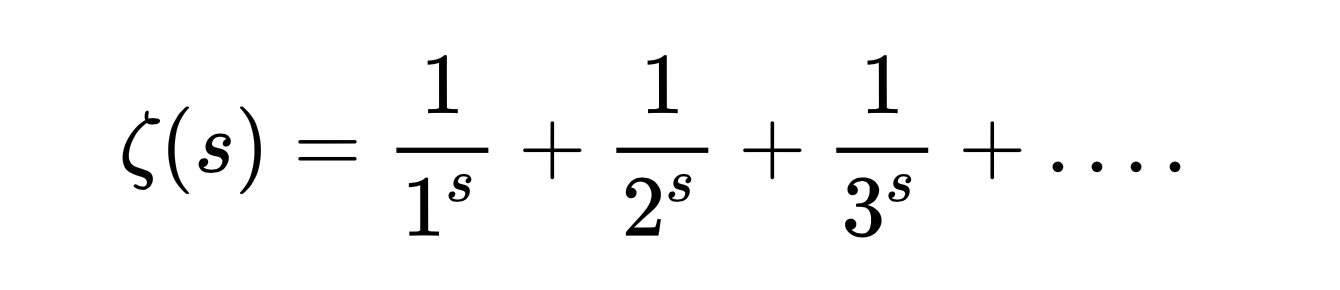
Переменная s в дзета-функции — комплéксное число. Если мы посмотрим на график дзета-функции Римана, то увидим точки, в которых она равна нулю — в этих точках s чаще всего равен отрицательным чётным числам:

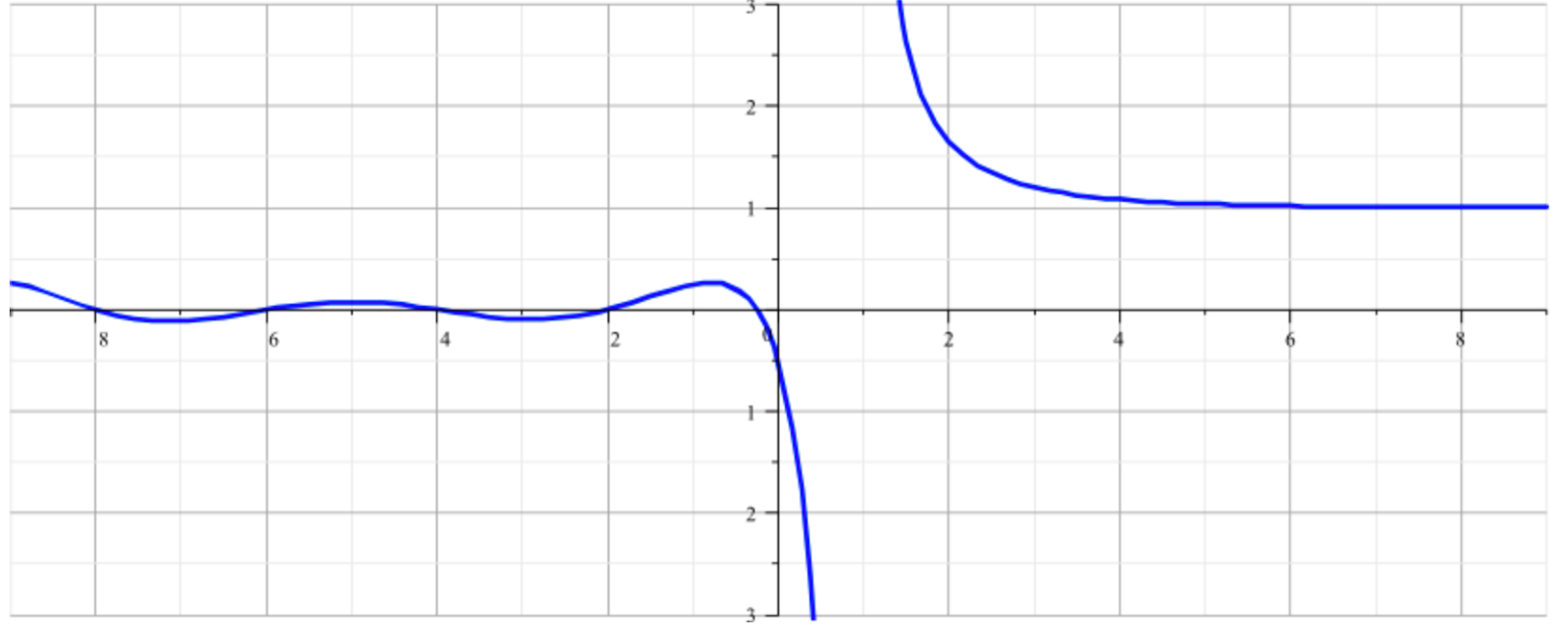
Эти видимые нули называются тривиальными нулями функции. Их довольно легко выявить — достаточно подставлять вместо s обычные числа. Но нам интересны нетривиальные нули: точки, где s принимает значения от 0 до 1, а дзета-функция при этом равна нулю. Оказывается, бывает и такое — уже найдено 10¹³ нетривиальных нулей.

Функция равна нулю в точках пересечения вещественной и мнимой частей, когда вещественная часть равна 1/2. Чему равна мнимая часть, точно сказать нельзя, потому что её невозможно выразить числом.

Так выглядит график, где красным показана вещественная часть комплéксного числа s, а синим — мнимая:

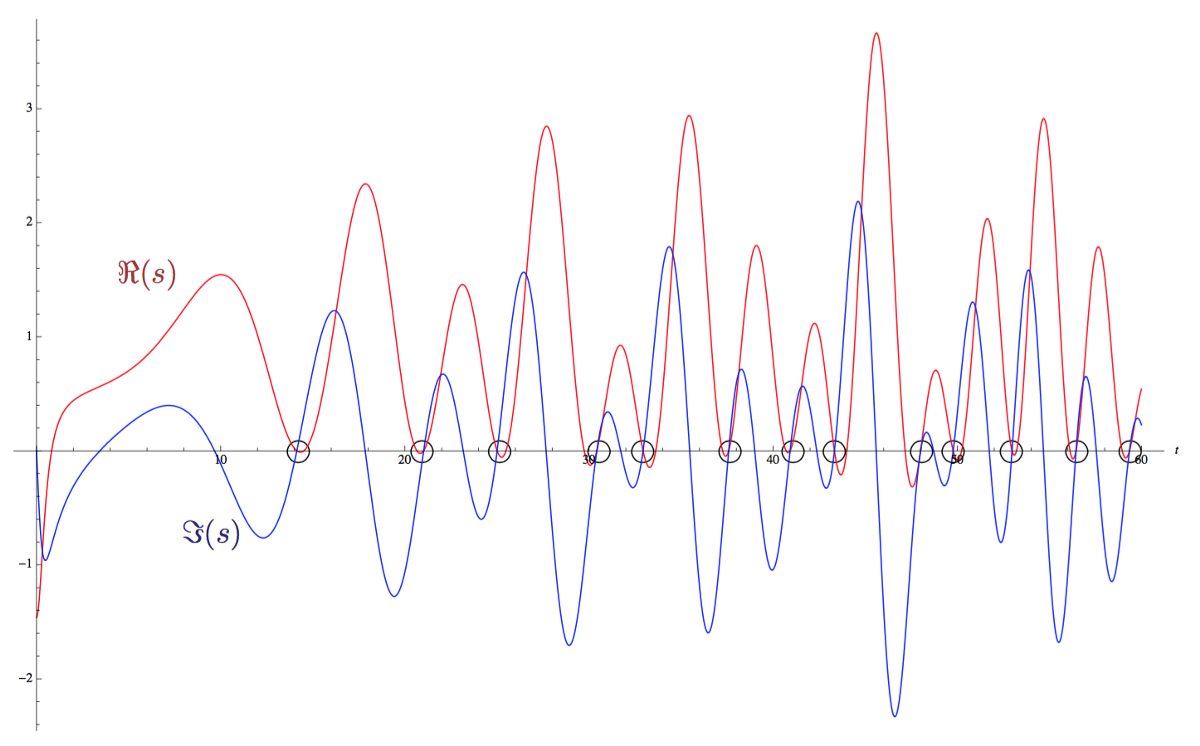
Теперь, наконец, мы можем попытаться понять гипотезу Римана:

Все нетривиальные нули дзета-функции имеют вещественную часть, равную 1/2

Это значит, что если ζ(s) = 0 на отрезке s от нуля до единицы, то s обязательно будет иметь вид 1/2 + bi.

В гипотезе Римана нет ни слова про простые числа. Но Риман предположил, что распределение нетривиальных нулей повторяет распределение простых чисел. Это подтвердится, если все нетривиальные нули дзета-функции действительно имеют вещественную часть, равную 1/2. Докажете это — миллион ваш.

Как хорошо нужно знать математику для решения

Нерешённые математические задачи остаются нерешёнными не потому, что в мире не хватает хороших математиков. Просто для ответа на них нужно время и особенный взгляд какого-то конкретного математика. А все усилия, которые тратят учёные для поиска решения, помогают двигать вперёд всю науку.

Главное, что задачи института Клэя вдохновляют на изучение разных разделов математики. Возможно, одна из задач ждёт именно вас :-)