В прошлый раз мы начали рассказывать про задачи тысячелетия — семь математических проблем, за решение каждой из которых Математический институт Клэя обещает миллион долларов США. Мы уже разобрали четыре из них, сегодня рассмотрим ещё две.
Кратко напомним, о чём речь:
- Институт Клэя в Кембридже поощряет развитие математики, выделяет гранты и премии. В 2000 году он объявил награду в один миллион долларов США за решение любой из 7 научных проблем. Для этого нужно найти однозначный ответ на гипотезу или вопрос — подтвердить, опровергнуть или доказать, что решения нет.
- Пока решена только одна задача — гипотеза Пуанкаре, которая уже не гипотеза, а теорема. Решил её россиянин Григорий Перельман.
- В прошлый раз мы рассказали про теорему Пуанкаре, гипотезы Ходжа и Римана и равенство классов P и NP.
Это очень крутая математика, так что, если вам что-то непонятно, это нормально, мы тоже долго разбирались. Но даже изучение того, как устроены такие теоремы и в чём их задача, развивает нестандартное мышление, которое необходимо программистам. Если вам интересно что-то более практичное и связанное с ИТ, попробуйте сделать свой конвертер из Markdown в Word.
Уравнение Навье — Стокса
Это задача из гидродинамики — раздела физики, который изучает движение жидкостей и газа и их взаимодействие с твёрдыми телами. Уравнение Навье — Стокса описывает движение жидкости, и вывели его Анри Навье и Джордж Стокс независимо друг от друга в разное время, поэтому уравнение носит их общее имя.
Вот что нужно кратко разобрать для понимания, о чём речь:
- производные,
- дифференциалы,
- дифференциальные уравнения,
- второй закон Ньютона.
Для решения этого не хватит, но за это мы не берёмся.
Производная показывает скорость роста функции и обозначается апострофом: x'. Чтоб посчитать производную, нужно умножить выражение на собственную степень, а саму степень уменьшить на 1. Например, (x2)' = 2 * x2-1 = 2x. Для производных суммы, разности и других выражений есть свои правила подсчёта, но для понимания задачи это необязательно.
Вот пример использования производной: допустим, каждый день мы читаем по одной главе из книги. Это стабильное движение, в котором ничего не меняется. Получается, что наша функция всегда равна тому числу, которое мы поставили изначально. Производная от постоянного равна 0, потому что роста нет:
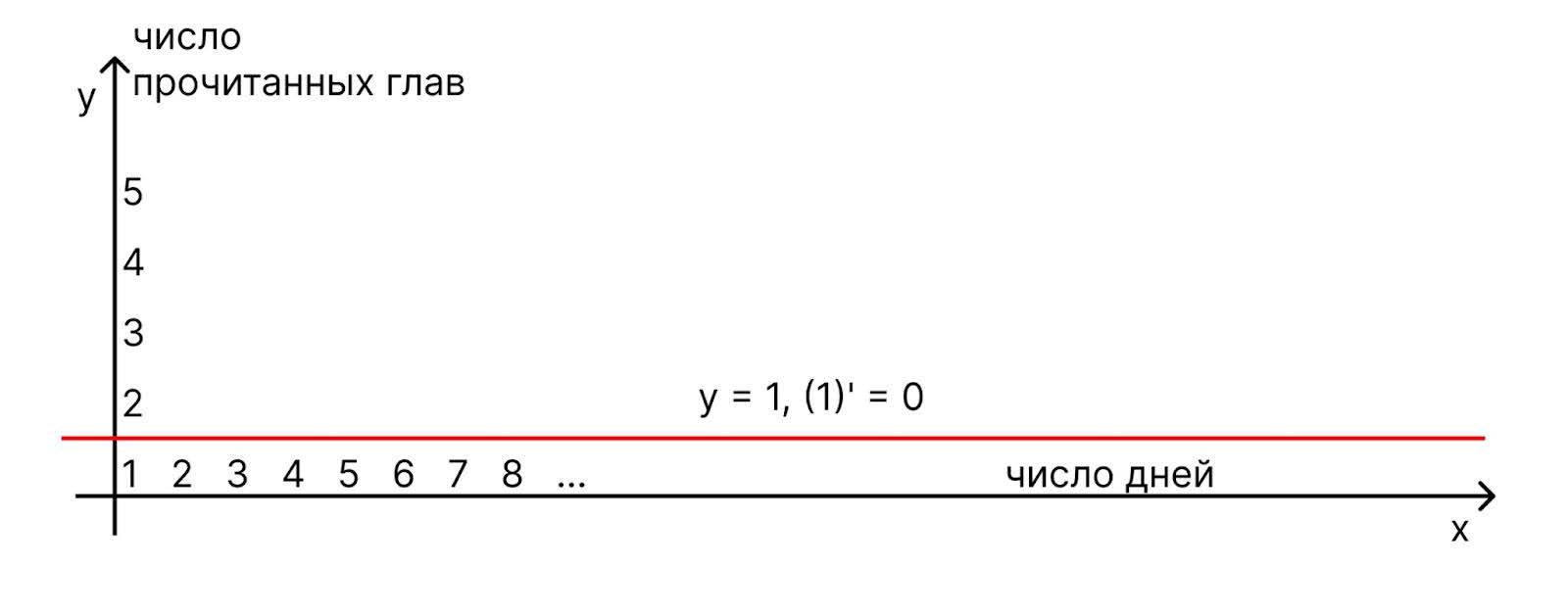
Если мы читаем каждый день на одну главу больше, чем вчера, получается тоже стабильно, но есть скорость роста: 1, 2, 3, 4, 5 глав — и так постоянно. Скорость роста в нашем случае равна 1. Зная эту зависимость, можно прогнозировать, сколько глав мы будем читать в день через месяц, если поддерживать такой темп:
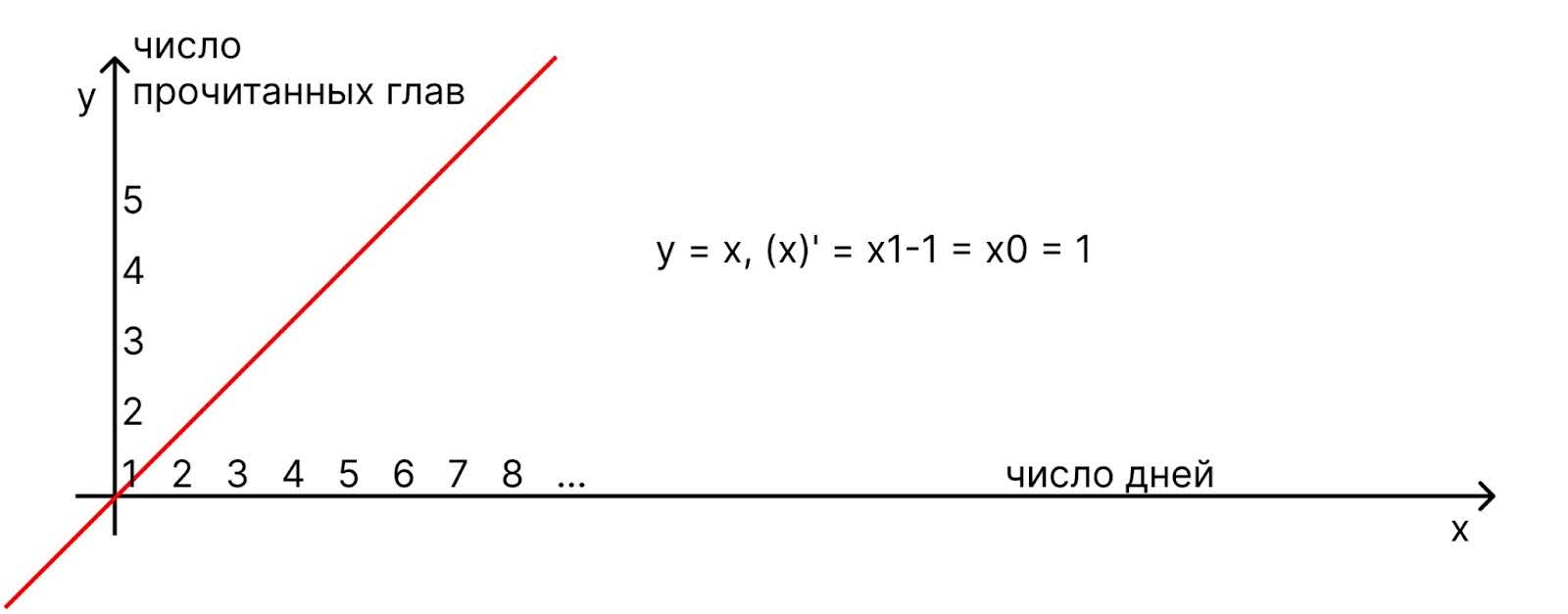
Если читать каждый день разное количество глав, то простым уравнением такое движение не задать. Но если у нас всё-таки получится, то можно будет посчитать от него производную и узнать, чему будет равен результат в какой-то момент в будущем.
Вот ещё два факта, которые понадобятся для понимания уравнения Навье — Стокса:
- Можно посчитать производную от производной. Это будет производная второго порядка:
x''. - Иногда в функции больше одного аргумента. Производная такой функции называется частной и считается для каждого аргумента отдельно.
Дифференциал — это увеличение сложной функции на каком-то участке аргумента, если бы функция была простой, линейной. То есть это линейное приращение функции. Звучит непонятно, но вот посмотрите: у нас есть график функции — какая-то кривая красная линия. Мы её сильно упростили и построили зелёную прямую. Она проходит по касательной из любой нужной нам точки:
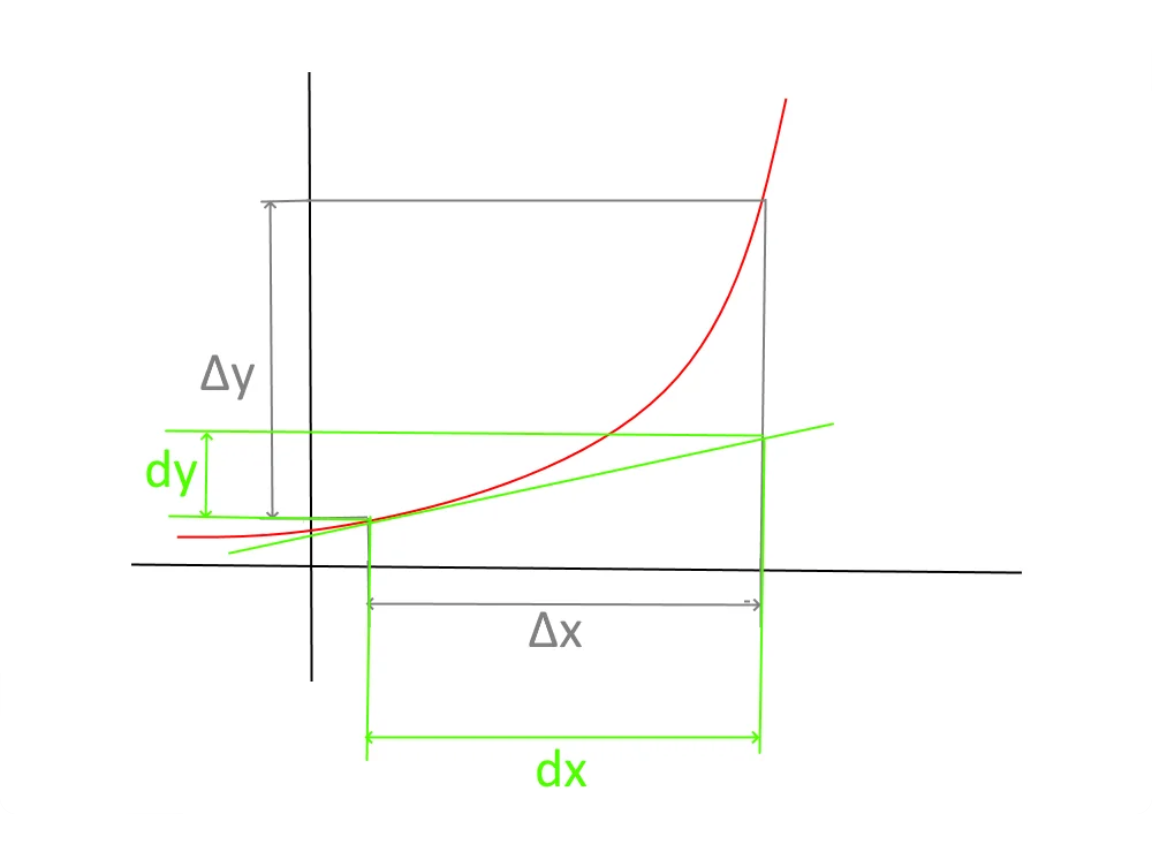
Δx (читается «дельта-икс») — это участок аргумента, на котором мы построили дифференциал аргумента dx и дифференциал функции dy. Конечно, линейное изменение dy мало похоже на реальное изменение Δy. Но если бы мы взяли участок Δx поменьше, то и разница была бы не такая большая. Иногда это важно, потому что позволяет упрощённо посчитать скорость роста, то есть упрощённую производную:
Δy/Δx = примерное значение производной функции f'(x)
Дифференциальные уравнения — это уравнения, которые, кроме функции, содержат её производные или дифференциалы. В нём будут обозначения вида y' или Δy и Δx. У дифференциального уравнения тоже есть порядок: он равен самому высокому порядку входящих в него производных. В отличие от уравнений, где мы ищем неизвестные, в дифференциальном нужно найти функцию.
Вот пример дифференциального уравнения. В него входят производные второго порядка и первого. Второго больше, поэтому всё уравнение тоже второго порядка:
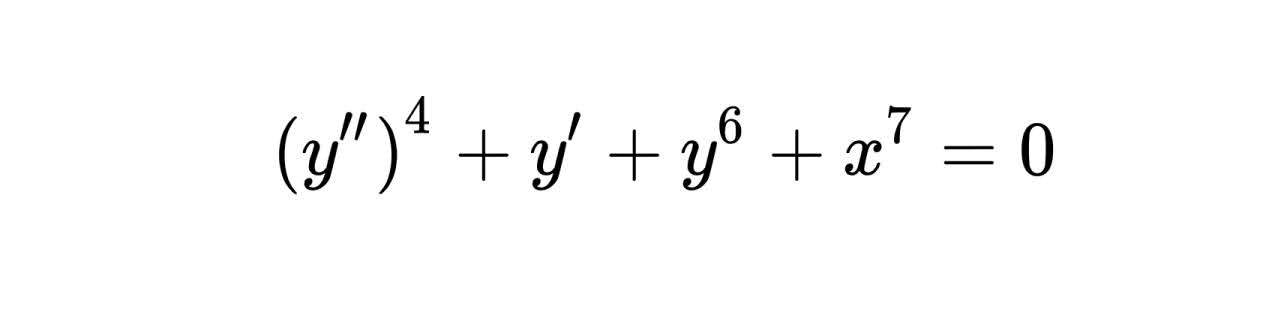
Второй закон Ньютона звучит так:
Величина силы, действующая на тело, равна произведению массы тела на ускорение, которое получает тело, когда на него начинает действовать сила.
Это значит, что если какой-то объект движется с изменением скорости, то на него действует какая-то сила. Например, шарик катится по земле, замедляется и останавливается. Изменение в скорости вызвано силой гравитации и трения. То, что шарик вообще покатился, тоже вызвано внешней силой: это мы его подтолкнули. Так выглядит формула второго закона Ньютона:
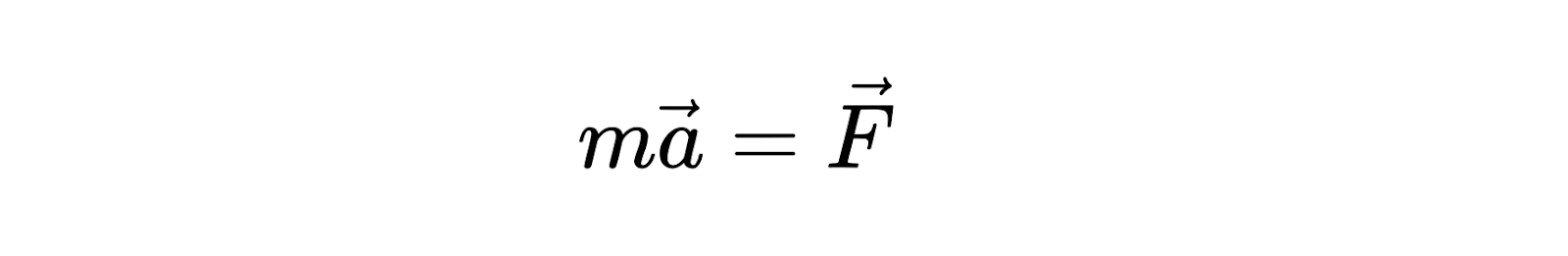
В ней три составляющие:
- m — масса тела;
- а — ускорение;
- F — сумма всех сил, действующих на тело.
Стрелочки над ускорением a и силой F означают, что у них есть направление — такие величины называются векторными.
Теперь перейдём к проблеме тысячелетия. Можно сказать, что уравнение Навье — Стокса — это как второй закон Ньютона, только в применении к несжимаемым вязким ньютоновским жидкостям с такими свойствами:
- вязкая жидкость сопротивляется, когда её перемещают;
- несжимаемая не меняет плотность при давлении;
- ньютоновская продолжает течь даже под действием сил минимальной величины — главное, чтобы силы были ненулевые.
Примеры жидкостей разной вязкости — мёд, кленовый сироп, кукурузный сироп и жидкое мыло:

Если речь идёт о шарике или падающем с дерева яблоке, к ним отлично подходит второй закон Ньютона. Нам важна не их внутренняя структура, а только масса. В любой точке яблока или шарика скорость и ускорение будут одинаковыми.
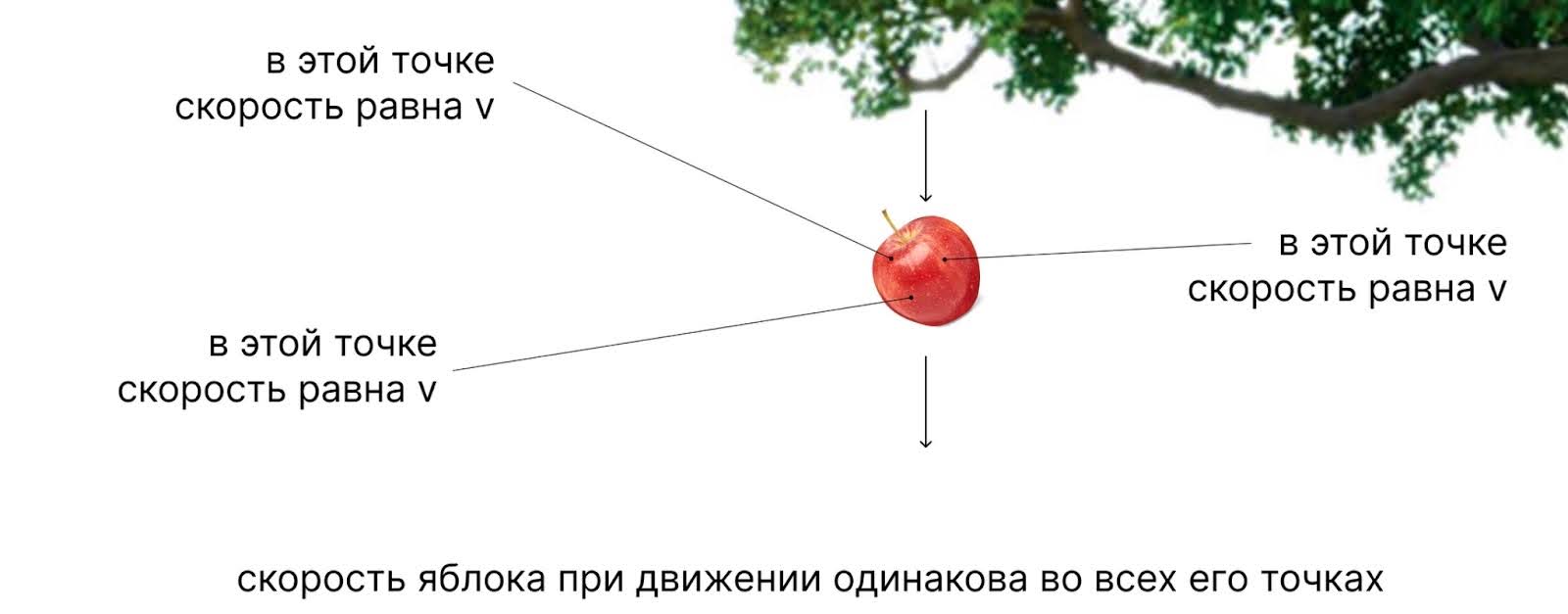
Жидкость течёт неоднородно, давление и скорость в разных точках различаются:

Уравнение Навье — Стокса описывает движение жидкости в любых условиях. Это очень реалистичная сложная формула, поэтому в ней учитывается много деталей. Вместо простой формулы закона Ньютона получилось дифференциальное уравнение с двумя неизвестными функциями — каждая больше чем с одним аргументом. Математически правильно назвать его дифференциальным уравнением в частных производных.
Разбирать подробно уравнение этой задачи тысячелетия мы не станем, но выглядит оно так:
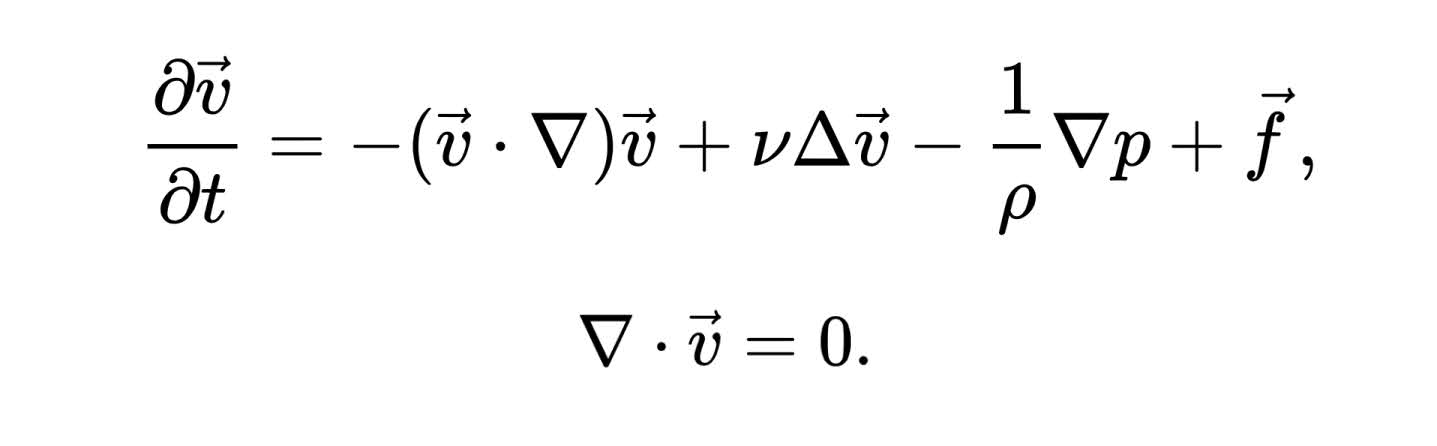
Неизвестные функции в уравнении — скорость и давление. Уравнение несжимаемости идёт отдельно — внизу после запятой.
Для решения задачи института Клэя нужно ответить на вопрос:
Если известно начальное состояние жидкости, есть ли решение для любого будущего момента времени?
Задача очень абстрактная, для неё даже не требуется явного решения. Просто сказать — да или нет. Ну и доказать, конечно.
Гипотеза Бёрча — Свиннертон-Дайера
Это задача из алгебраической геометрии про эллиптические кривые. Возможно, она самая сложная задача для понимания из всех в списке Института Клэя. Задача затрагивает и теорию чисел, и алгебраическую геометрию, и топологию, и даже модульную арифметику. Попробуем разобрать, что нужно для её понимания:
- степень уравнения;
- эллиптические кривые;
- род и ранг кривой;
- гипотеза Морделла;
- сравнение по модулю.
Степенью уравнения называют наивысшую степень неизвестного. Например:
x + 15 = 20— уравнение первой степени (линейное);x2 + 5x - 3 = 0— уравнение второй степени (квадратное);x3 = 13— уравнение третьей степени (кубическое).
График линейной функции от уравнения первой степени будет прямой линией:
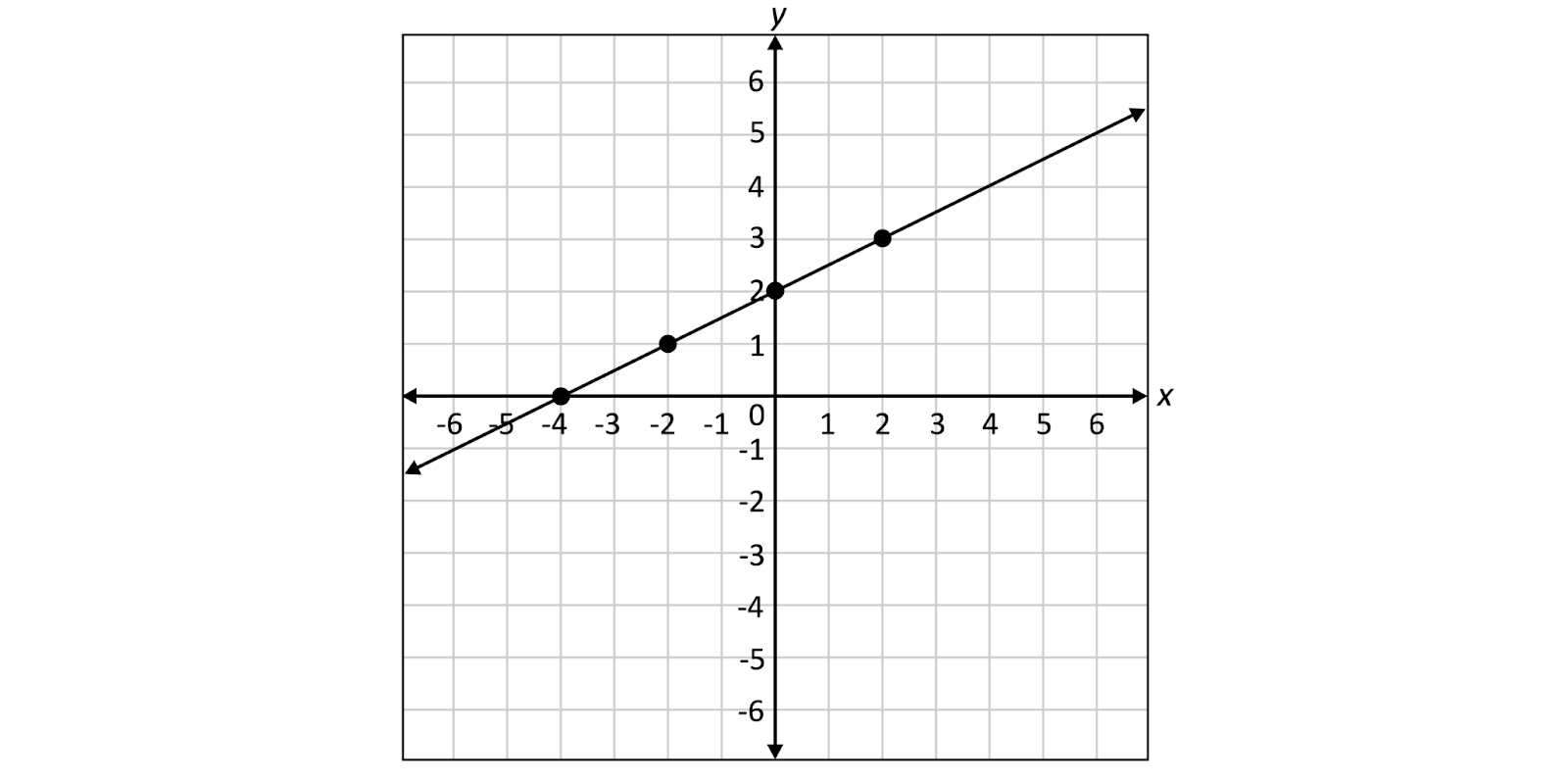
Кривые, которые получаются от графиков квадратных уравнений, называются кониками. Они повторяют разрез конуса в разных местах, в результате чего образуются параболы, эллипсы, окружности и гиперболы:
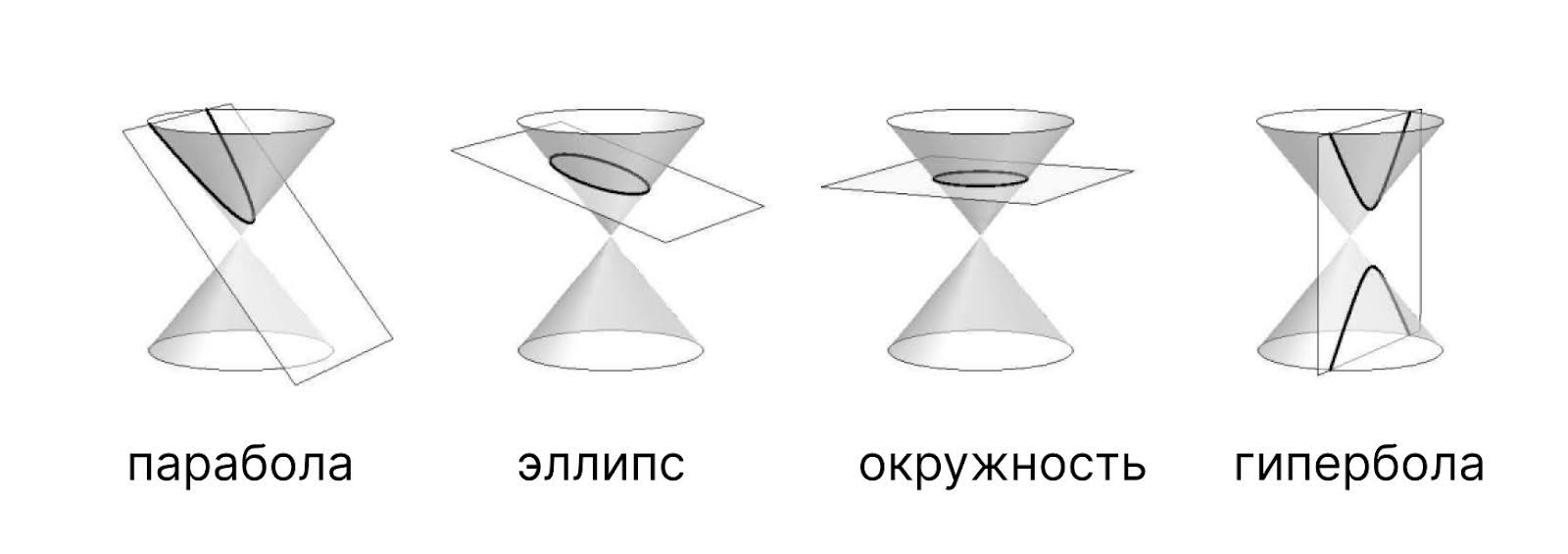
Эллиптические кривые — это графики функций кубических уравнений одного определённого вида: y2 = x3 + ax + b. Этот вид уравнений называется уравнениями Вейерштрасса. Выглядеть они могут по-разному, например так:
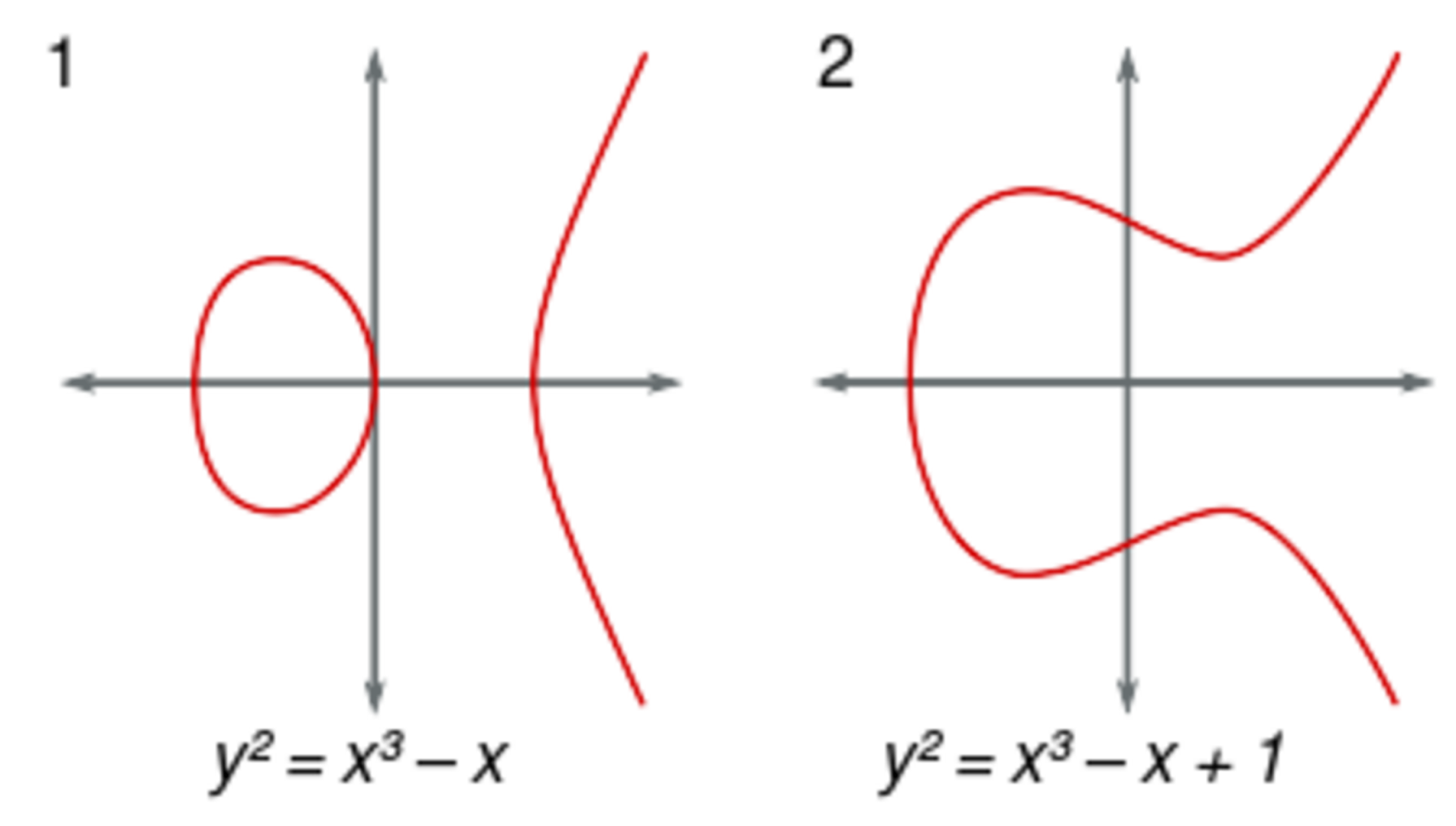
Ещё раз: все эти кривые — на самом деле уравнения, поэтому у них есть корни.
В теореме Бёрча — Свиннертон-Дайера много говорится конкретно про рациональные корни, поэтому быстро напомним, что это:
- Рациональные числа можно представить в виде обычной дроби из целых чисел:
1/2,3/3,15/1,13/17. - Иррациональные числа нельзя представить в виде обычной дроби:
√2,число π,число Эйлера e.
Когда говорят, что уравнение или кривая имеет бесконечное число рациональных точек или решений, имеют в виду, что для решения подходит бесконечное количество рациональных чисел.
Род и ранг кривой — ещё два понятия, которые нужны нам для теоремы. Сначала род. В прошлой статье мы немного рассказали про свойства трёхмерных фигур. Что нужно знать сейчас:
- Фигуры, как и кривые, можно описывать уравнениями.
- Бывают фигуры с отверстиями. Пример — тор, математический бублик. У тора есть отверстие, а у куба или сферы нет. Количество отверстий фигуры называют родом. Род сферы равен 0, а род тора равен 1.
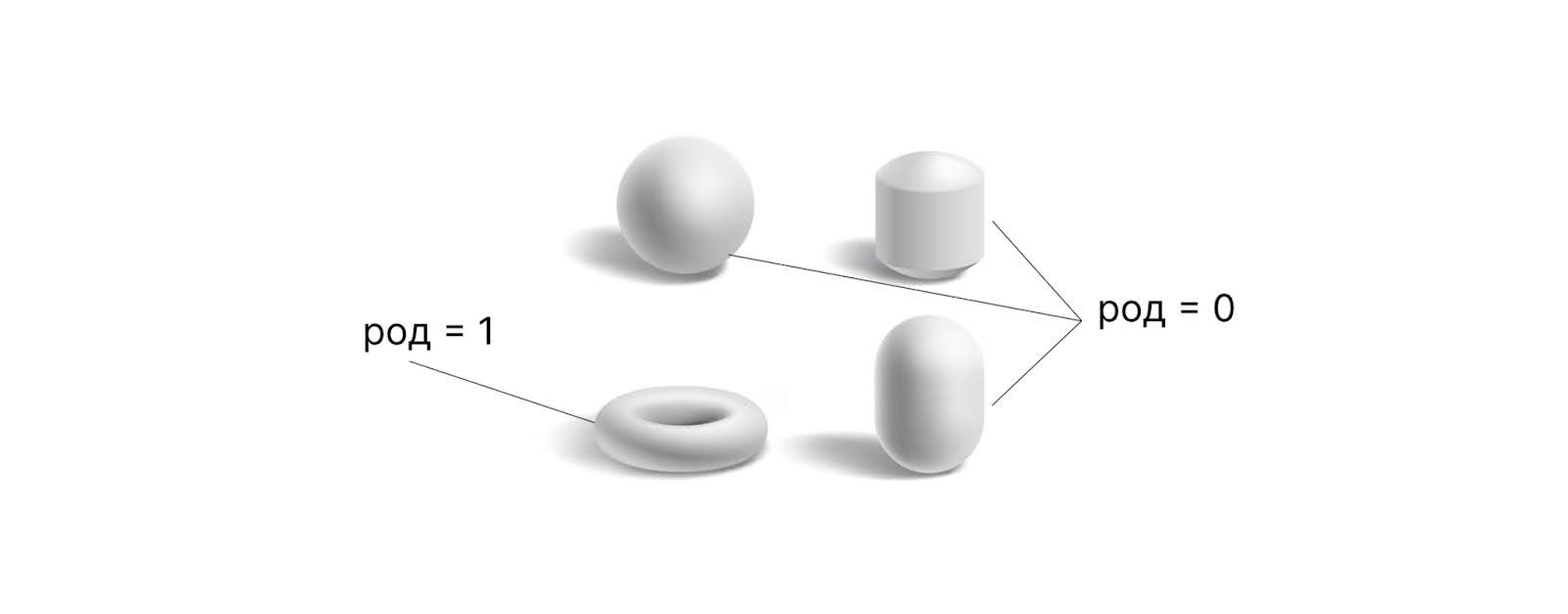
Гипотеза Морделла гласит:
- количество рациональных точек для уравнения фигуры зависит от её рода;
- фигуре с родом, равным 1, может соответствовать эллиптическая кривая с ограниченным количеством рациональных точек.
Род эллиптических кривых всегда равен 1. Это связано не с отверстиями на графике, а со связью между фигурами и кривыми. Важное и неочевидное следствие гипотезы Морделла состоит в том, что если мы знаем несколько рациональных корней такой эллиптической кривой, то можем найти все.
Но у эллиптической кривой может не быть рациональных точек, такая вероятность тоже есть. Поэтому сложность в том, чтобы понять, что у кривой конечное количество рациональных точек. У эллиптических кривых есть важное свойство: если мы проведём на графике прямую, пересекающую кривую в двух рациональных точках, то третья точка пересечения тоже будет рациональной:
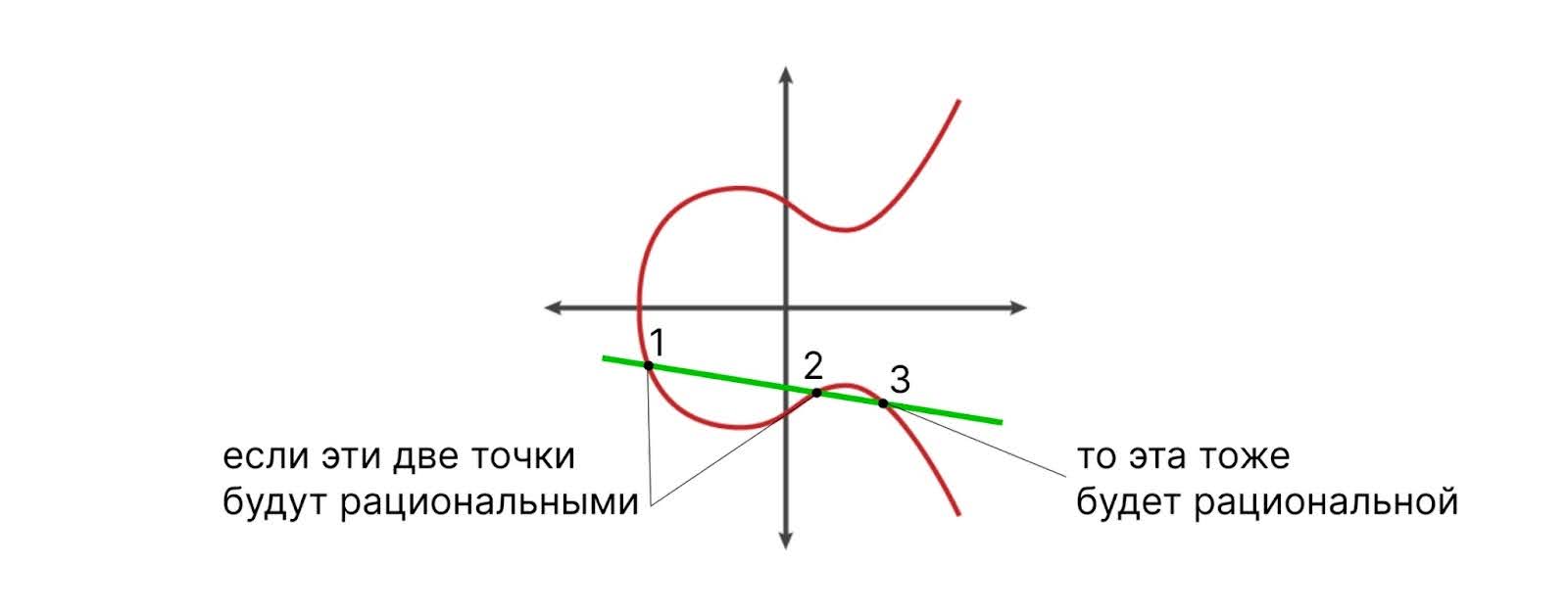
При этом необязательно, что для определения всех рациональных точек нам хватит только первых двух.
Ранг кривой — это количество необходимых известных рациональных точек для определения всех остальных. Но общего алгоритма для вычисления этого минимального количества нет.
Сравнение по модулю — самая сложная часть. Для анализа эллиптических кривых анализируют их решения через простые числа. Это сложный процесс, вот основной алгоритм и правила:
- выбираем уравнение эллиптической кривой для анализа, для примера возьмём
y2 = x3 - 5x; - берём простое число, например 5;
xиyв нашем уравнении должны принимать значения от 0 до 4, потому что последнее число диапазона меньше простого числа на 1;- берём все значения от 0 до 4 по порядку, подставляем в уравнение и считаем.
На этом месте остановимся. Мы подставили на место x настоящее число и подсчитали правую часть уравнения. От результата зависит, сколько решений имеет эллиптическая кривая для конкретного x (именно для него, а не для всего простого числа 5).
Если получилось, что y2 = 0, то у кривой есть одно решение. Тогда говорят, что для x = 0 есть одно решение по модулю 5.
Теперь допустим, что у нас получилось что-то другое. Например, для x = 2 получаем, что y2 = 3. Нужно проверить: возможно ли, что есть натуральное число от 0 до 4, которое при возведении в квадрат и делении на 5 (это наше простое число) даст тот же остаток, что и 3 при делении на 5?
Математически это записывается так: y2 ≡ 3 (mod 5). Тройное равно означает «тождественно равно», а mod 5 — по модулю 5. Если выражение неверно, то для выбранного x решений нет. Если верно, то решениями будут все y, при которых это тождественное равенство выполняется.
Смотрим, что получается у нас. Проверяем правую часть: остаток от деления 3 на 5 равен 3. Теперь подставляем на место y числа от 0 до 4:
- 02 = 0 при делении на 5 даёт 0, остаток тоже 0;
- 12 = 1 при делении на 5 даст 0, остаток 1;
- 22 = 4 при делении на 5 даст 0, остаток 4;
- 32 = 9 при делении на 5 даст 1, остаток 4;
- 42 = 16 при делении на 5 даст 3, остаток 1.
Ни одно число из списка не даёт тот же остаток, что 3, поэтому для x = 2 решений нет.
Когда мы прошли весь список от 0 до 4, нужно посчитать количество существующих решений. Это количество будет соответствовать одному простому числу — в нашем случае 5. Если проверить таким модульным анализом список простых чисел, например от 0 до 1 000 000, то можно составить таблицу, где под каждым простым числом будет количество решений для конкретного уравнения эллиптической кривой:
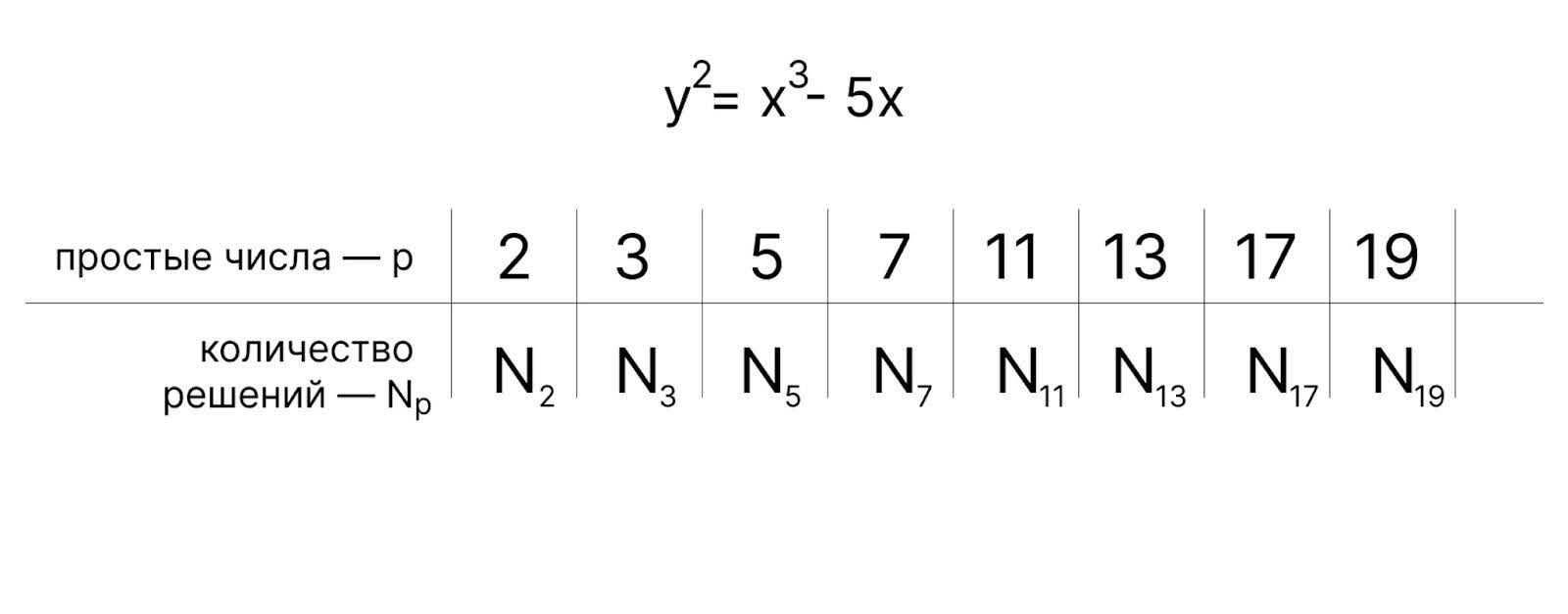
Вот в чём состоит открытие, которое сделали два английских математика Брайан Бёрч и Питер Свиннертон-Дайер. Если построить график, где по горизонтальной оси откладывать простые числа p, а по вертикальной — количество решений Np, то график будет выглядеть как набор точек, но примерный наклон этого графика равен рангу эллиптической кривой, над которой провели анализ по модулю:
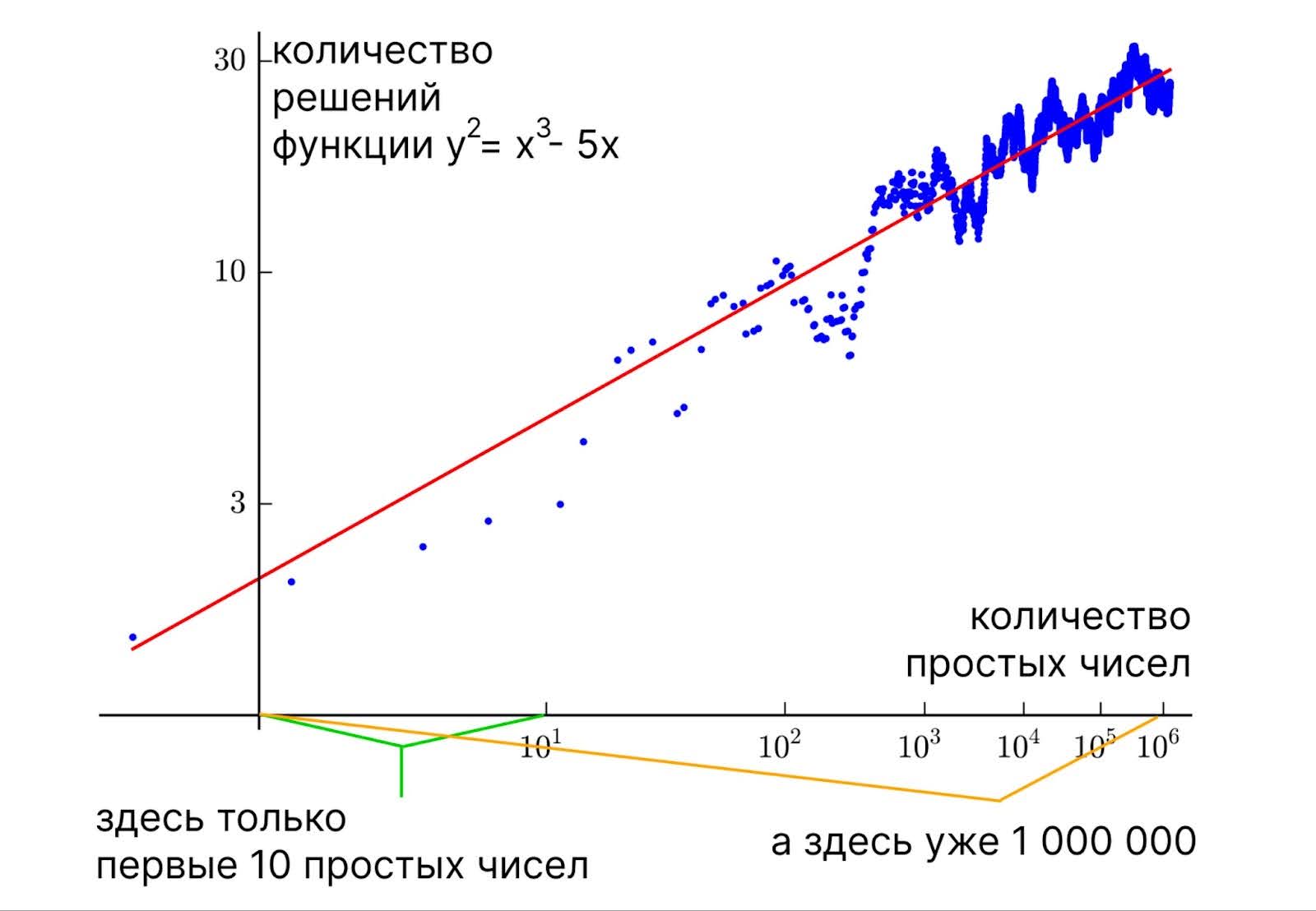
Наклон на этом графике равен 1. Ранг кривой — тоже 1. Если на этом месте вам всё ещё хочется знать, что нужно доказать, то вам в Институт Клэя:
Для решения нужно подтвердить или опровергнуть, что наклон графика анализа решений по модулю простых чисел всегда равен рангу кривой.
Что осталось
Осталась ещё одна задача в списке Института Клэя, которую мы не разобрали: теория Янга — Миллса. Это самая объёмная проблема, поэтому о ней расскажем в следующий раз.













