Один джуниор пришёл на собеседование в крупную ИТ-компанию, и ему дали тест из 50 вопросов. За каждый правильный ответ он получал 9 баллов, а за каждый неправильный отнимали 17 баллов. Если же просто пропустить вопрос, то за него ничего не давали и не списывали.
Чтобы устроиться на работу, нужно или набрать 170 баллов в тесте, или дать больше 30 правильных ответов. Джуниор набрал 153 балла, при этом он точно знал, что как минимум в одном вопросе он ошибся.
Взяли ли его на работу?
Мы не знаем, как отвечал джуниор, поэтому обозначим всё так:
x — количество правильных ответов
y — количество неправильных ответов
z — сколько вопросов осталось без ответа.
При этом мы помним, что джуниор точно ошибся как минимум в одном вопросе, поэтому игрек у нас будет больше либо равен единице.
Зная, что всего вопросов было 50, можем составить уравнение: x + y + z = 50.
Так как за каждый правильный ответ джуниор получал 9 баллов, а за неправильный снималось 17, составим второе уравнение: 9x − 17y + 0z = 153.
Получаем систему из двух уравнений:
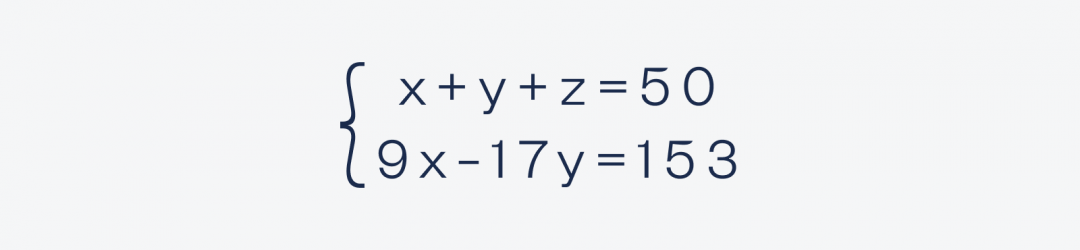
Второе уравнение выглядит проще, поэтому займёмся им.
9x − 17y = 153
9x − 153 = 17y ← вынесем здесь 9 за скобки, как множитель в левой стороне
9(x − 17) = 17y
В последнем уравнении видно, что левая часть делится на 9 без остатка (потому что там есть множитель 9). Это значит, что 17y тоже должно делиться на 9 без остатка, а раз 17 на 9 не делится, то делится игрек. Получается, что он может быть равен 9, 18, 27, 36 или 45 (больше быть не может, потому что общее число вопросов у нас 50).
Проверим все эти числа по очереди.
✅ Если y = 9, то (x − 17) = 17 (мы используем последний вид второго уравнения), а значит, x = 34. Если x = 34, то z = 50 − 34 − 9 = 7. Вроде сходится, но надо проверить остальное.
❌ Если y = 18 = 9 × 2, то (x − 17) = 17 × 2, а значит, x = 51. Но число вопросов у нас 50, поэтому y = 18 не подходит.
❌ Если y = 27 = 9 × 3, то (x − 17) = 17 × 3, а значит, x = 68. Но число вопросов у нас 50, поэтому y = 27 не подходит.
❌ Видно, что с ростом игрека у нас начинает сильно расти x, который давно выбился за допустимые 50 вопросов, поэтому остальные варианты (36 и 45) тоже не подходят.
А раз так, то остаётся только один, самый первый вариант, где x = 34. Этого достаточно, чтобы джуниора взяли на работу.