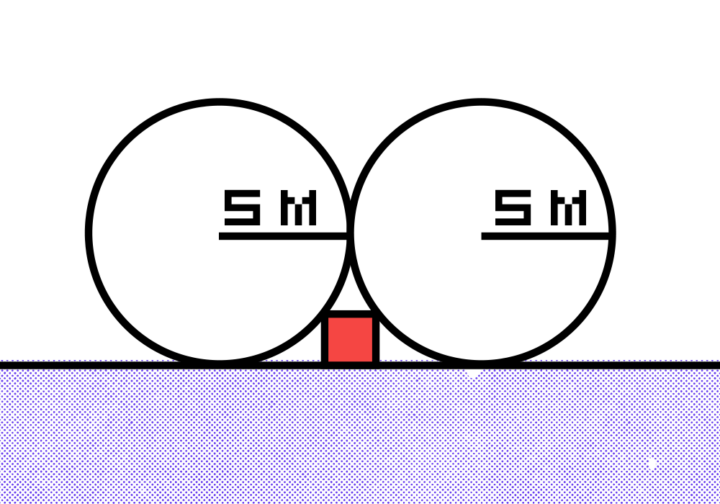
Недавно в сети завирусилась задачка про два круга и квадрат. Всё веселье в том, что она кажется очень сложной, но на самом деле решается довольно просто. Если сможете решить её, не заглядывая в наши подсказки, — приходите в ИТ, вы там точно будете на своём месте.
Теперь сама задачка.
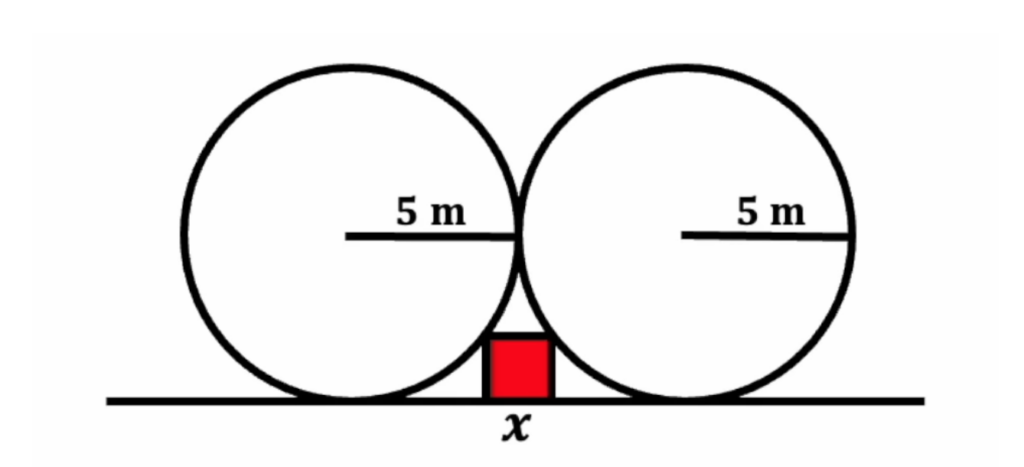
Есть два круга, которые стоят рядом на горизонтальной линии и касаются друг друга. Радиус каждого круга — 5 метров. Внизу под ними вписали квадрат, чтобы он касался кругов верхними углами. Нужно найти площадь этого квадрата.
На первый взгляд кажется, что для решения нужно знать много сложных формул из тригонометрии, синусы и вот это вот всё. Но на самом деле всё гораздо проще, следите за руками.
Первым делом опускаем перпендикуляр вниз из центра круга и потом проводим вторую линию — от центра до точки, где квадрат касается круга:
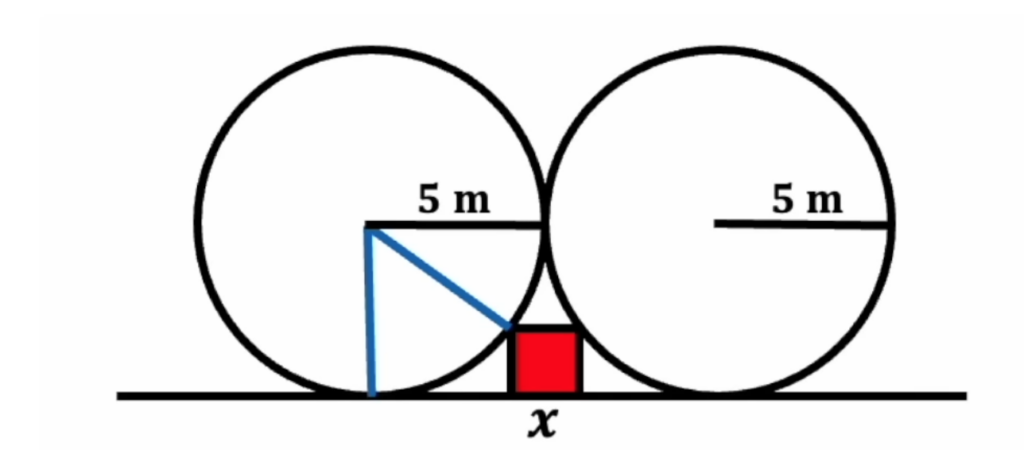
Все линии, которые исходят из центра круга и касаются его внешней стороны — это радиусы, поэтому каждая новая линия тоже имеет длину 5 метров. А раз мы опустили первую линию перпендикулярно линии, на которой стоит круг (как раз в точку касания основания), то этот угол равен 90 градусов:
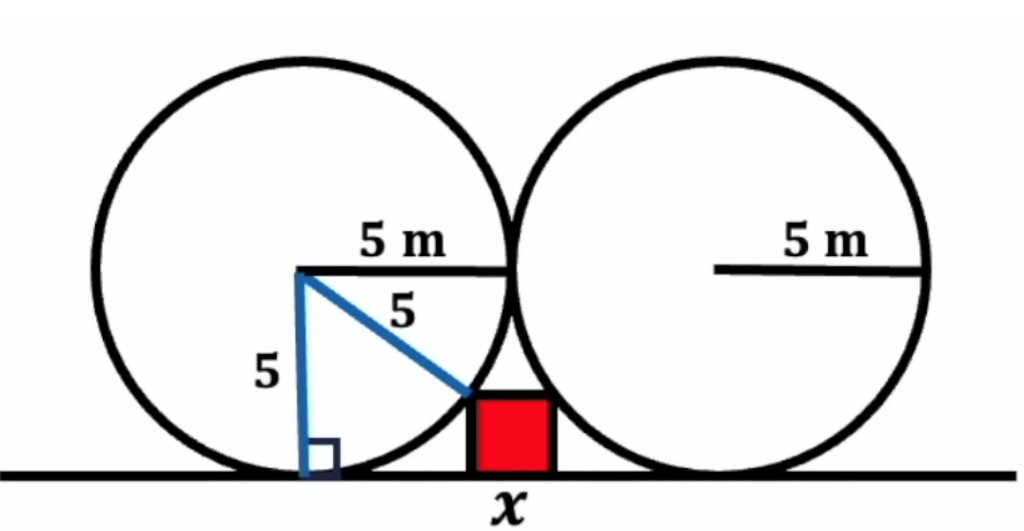
Теперь проведём от точки касания квадрата линию (зелёную), которая будет параллельна основанию до пересечения с нижним радиусом. В итоге мы получим угол тоже в 90 градусов между зелёной линией и радиусом. А раз так, то расстояние от точки пересечения до основания тоже будет равно Х:
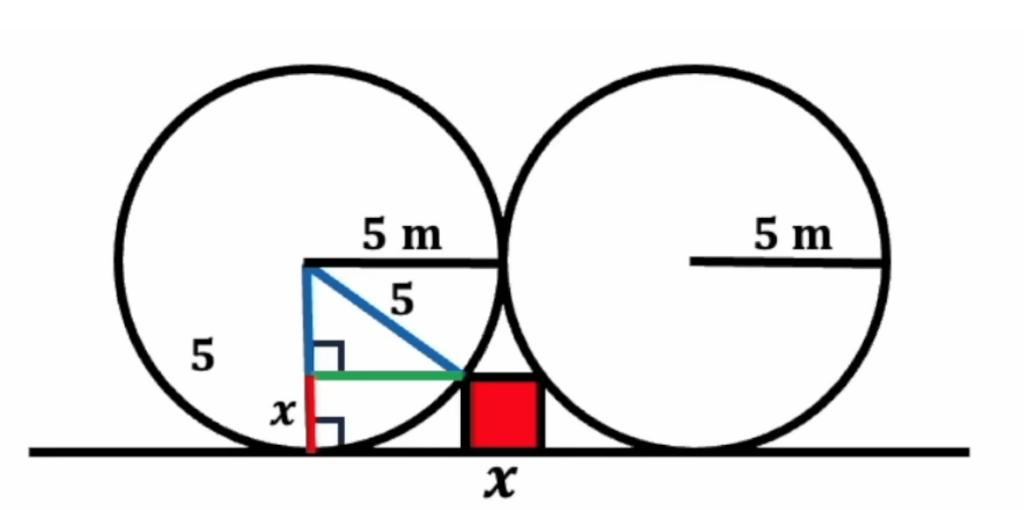
Раз нижняя часть первого нашего радиуса равна Х, а общая его длина равна 5 метрам, то оставшаяся часть равна (5 − Х) метрам. Единственное, что мы не знаем — длину той самой зелёной линии, поэтому обозначим её за Y:
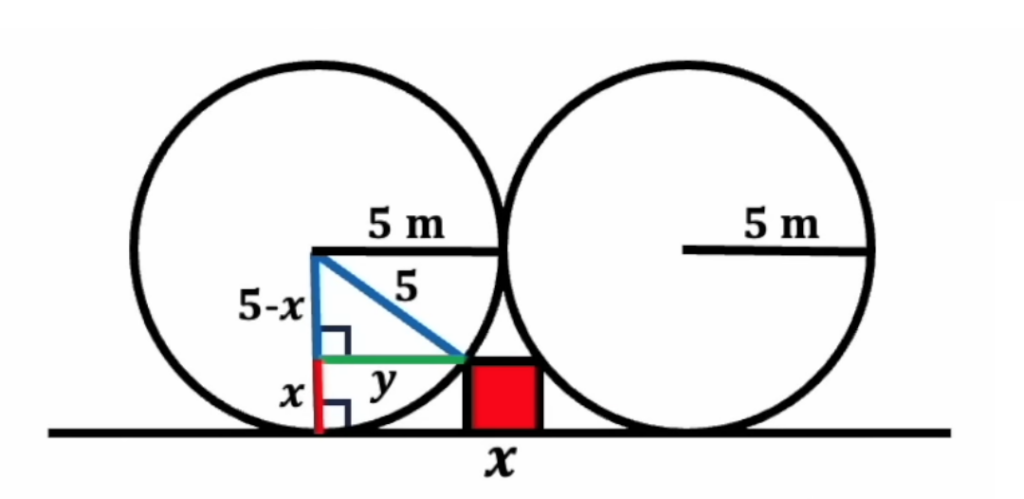
Теперь, когда у нас есть прямоугольный треугольник, мы можем использовать теорему Пифагора для того, чтобы найти значение Х с помощью формулы a² + b² = c². Подставим туда наши значения:
(5 − X)² + Y² = 5² ← раскроем скобки
25 − 10X + X² + Y² = 25
Y² = 10X − X²
Так как игрек в квадрате точно больше ноля, извлечём квадратный корень из обеих частей:
Y = √(10X − X²)
Запомним это значение и посмотрим на рисунок с другой стороны. В левом круге мы проводили зелёную линию от точки касания квадрата до радиуса, перпендикулярного основанию. Сделаем то же самое с другим кругом:
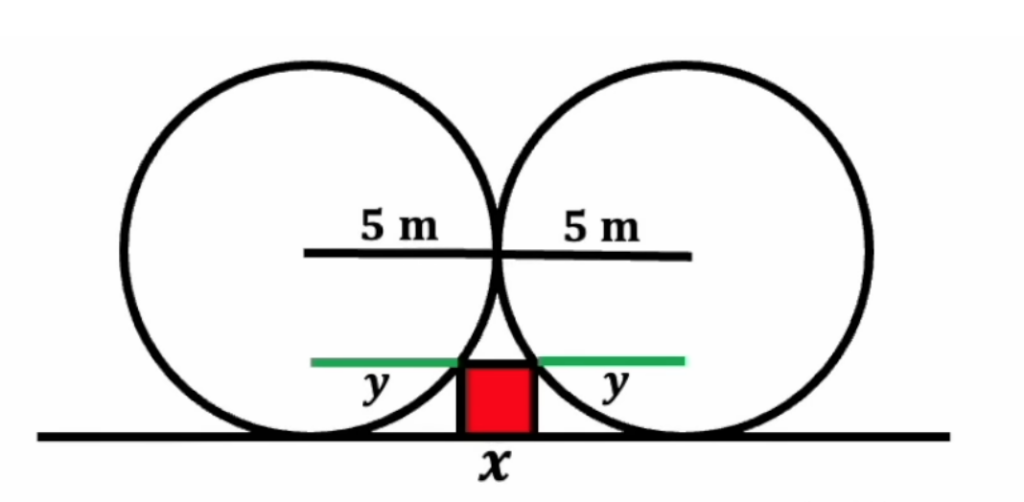
Так как слева и справа крайние точки верхних радиусов и нижних зелёных линий находятся на одной вертикальной прямой (потому что они перпендикулярны линии, проведённой под углом в 90 градусов к основанию), то общие длины этих отрезков равны:
Y + Y + X = 5 + 5
2Y + X = 10
Но мы помним, что Y = √(10X − X²), поэтому можем подставить это значение в текущее уравнение вместо игрека:
2√(10X − X²) + Х = 10 ← перенесём икс в правую часть
2√(10X − X²) = 10 − X
Так как значение квадратного корня больше нуля, то мы можем возвести обе части в квадрат, чтобы избавиться от корня:
4(10X − X²) = (10 − X)²
40X − 4X² = 100 − 20X + X² ← сделаем из этого обычное квадратное уравнение
5X² − 60X + 100 = 0
Раз все три слагаемых делятся на 5, то разделим, чтобы упростить решение:
X² − 12X + 20 = 0
Решаем это простое квадратное уравнение и получаем два решения, одно из которых точно не подходит:
X = 10 ← это не подходит, потому что явно больше радиуса каждого круга
X = 2 ← а это — подходит
Получается, что сторона квадрата равна двум метрам, а общая его площадь — 2 × 2 = 4 квадратных метра!
Как видите, никакой сложной математики — только простая логика и неспешные вычисления.