В одной из статей мы говорили о транзисторах и о том, как они устроены. Сегодня будет практика — мы соберём из транзисторов XOR и выясним, сколько для этого нужно транзисторов.
Коротко о транзисторах
Чтобы лучше понять, что будет дальше, напомним, что такое транзистор. Если хотите копнуть поглубже, почитайте наш разбор:
Транзисторы выполняют всю компьютерную работу: считают, запускают программы, управляют датчиками и отвечают за работу устройства в целом.

При этом сам транзистор — простейший прибор, который, по сути, похож на кран или электрические ворота. Через транзистор идёт какой-то один ток, а другим током этот поток можно либо пропустить, либо заблокировать. И всё.
Вот примерная схема. В жизни ножки транзистора могут быть расположены не так, как на схеме, но для наглядности нам надо именно так:
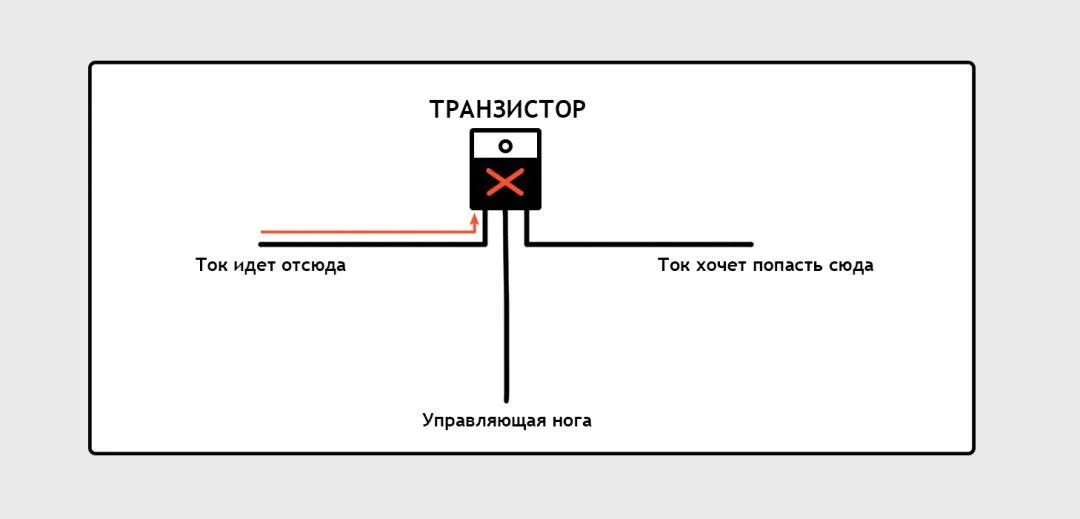
Ток пытается пройти сквозь транзистор, но транзистор «закрыт»: на его управляющую ногу не подан другой ток.
А теперь мы подали на управляющую ногу немного тока, и транзистор «открылся» и пропускает через себя основной ток.
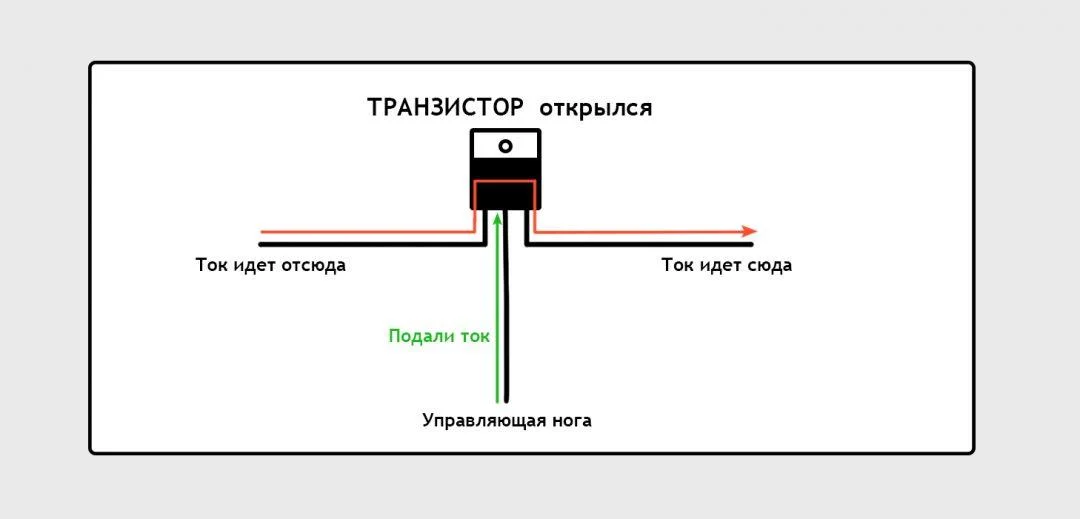
Из миллиардов таких простейших «кранов» и состоит любая современная вычислительная машина: от чайника с электронным управлением до суперкомпьютера в подвалах Пентагона. И до чипа в вашем смартфоне.
Что такое XOR и где это применяется
XOR — исключающее «или». Оно сравнивает два элемента и, если они равны, возвращает 0, а если разные — 1. XOR широко используется в процессорах для выполнения простейших математических операций. Ну и идеологически это основа всей сложной программистской логики: любой оператор сравнения в вашей программе так или иначе будет опираться на работу XOR.
0 XOR 0 = 0
1 XOR 0 = 1
0 XOR 1 = 1
1 XOR 1 = 0
Собираем XOR из транзисторов
Если мы откроем любой учебник по матлогике, там будет написано, как с помощью И, ИЛИ и НЕ получить XOR. Похоже на сложное нечитаемое заклинание:
(НЕ(a) И b) ИЛИ (а И НЕ(b))
Мы уже знаем, как сделать на транзисторах все эти элементы, поэтому просто соберём их в одно целое.
НЕ(a) :И b:
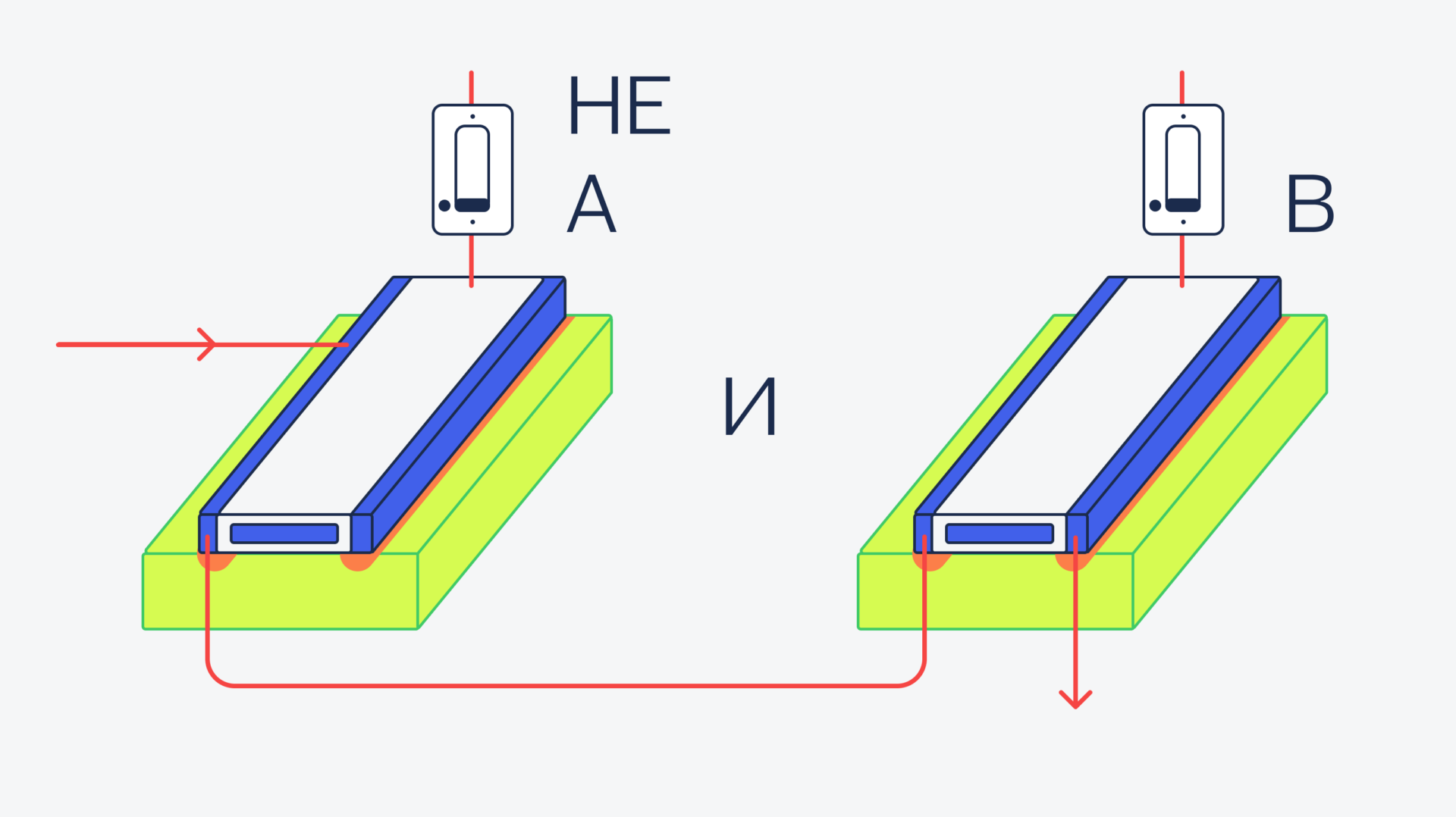
а И НЕ(b):
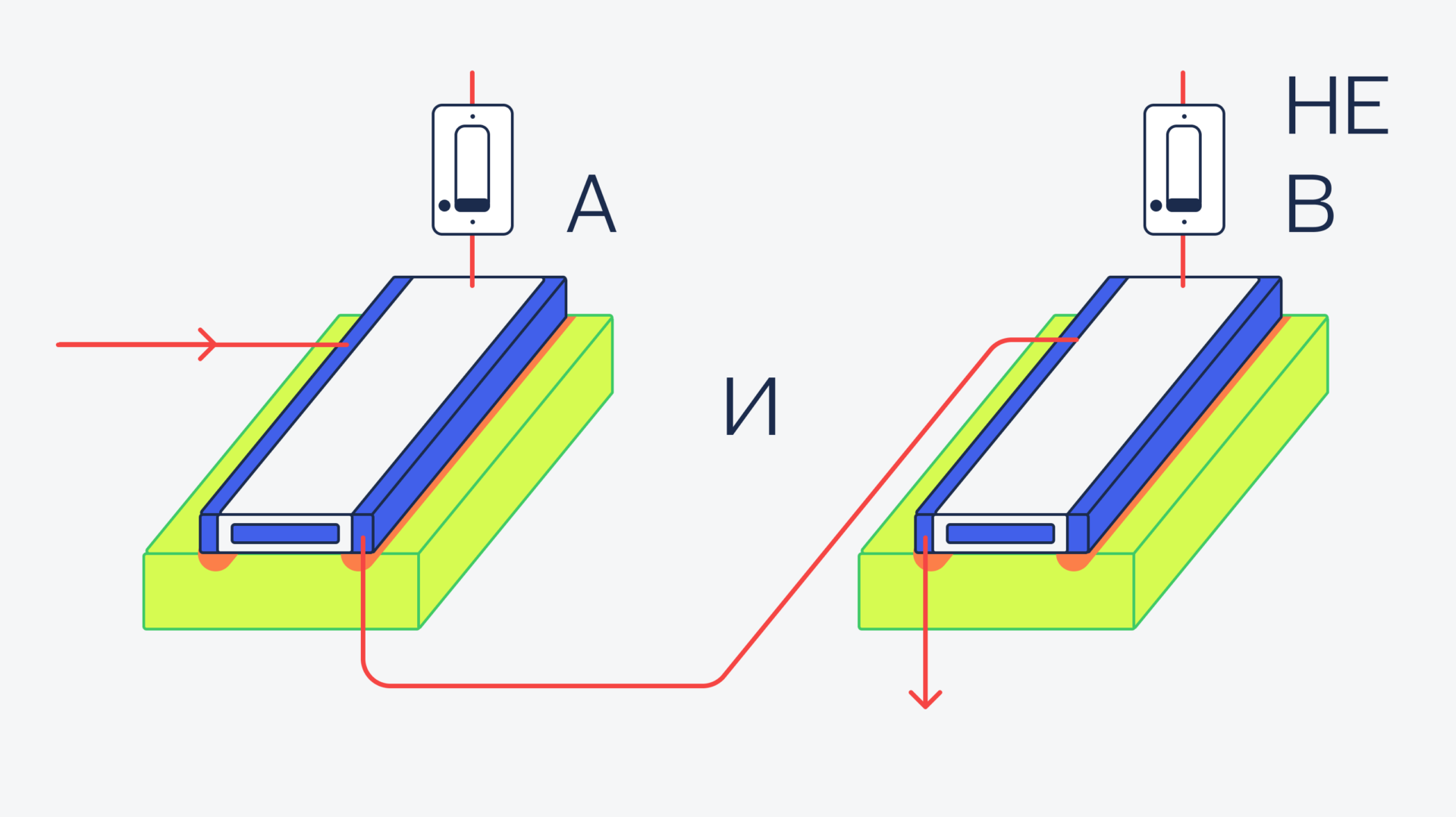
Теперь объединим это в одно целое, используя логическое ИЛИ.
(НЕ(a) И b) ИЛИ (а И НЕ(b)):
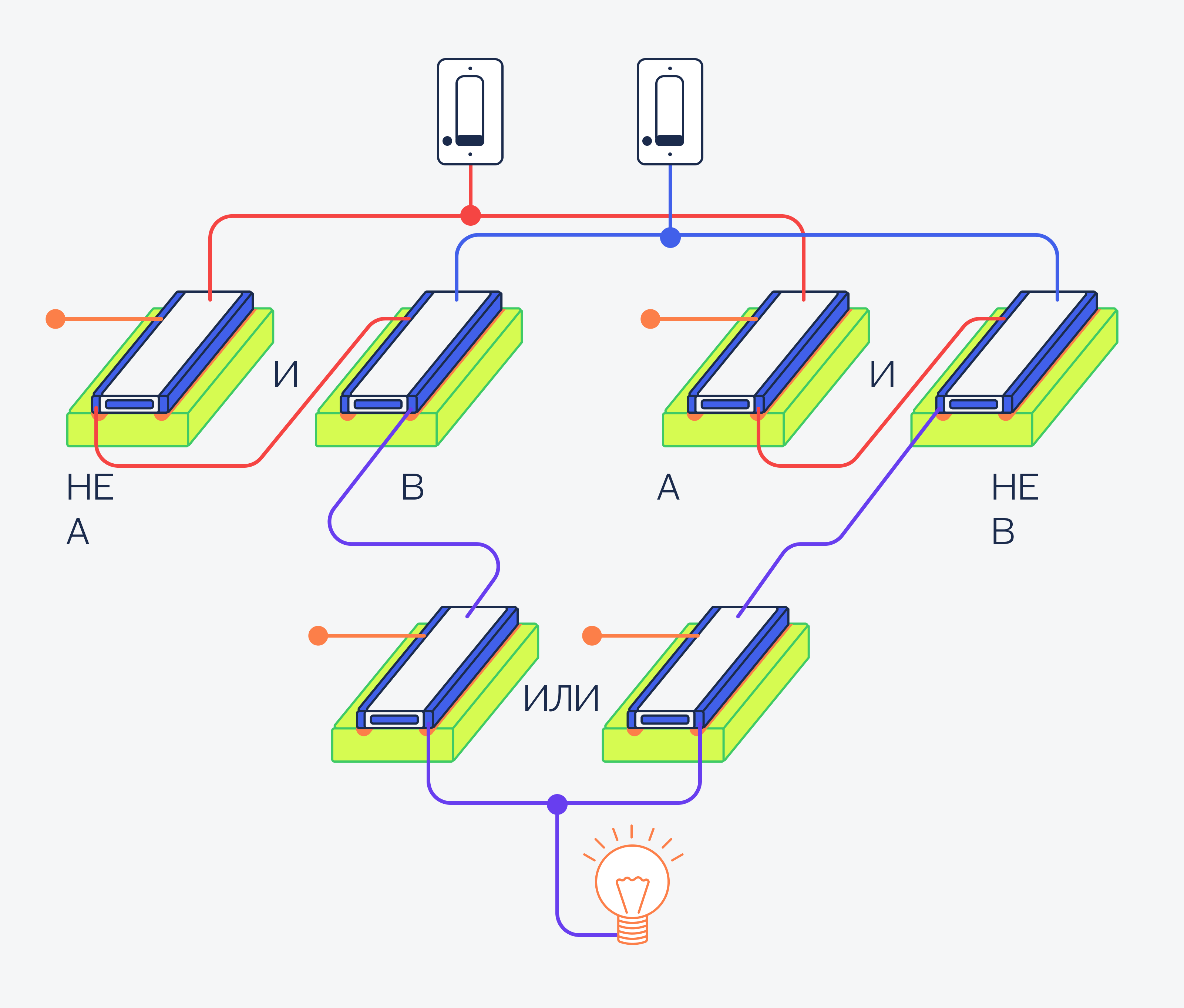
На схемах XOR обозначается так:
Выглядит громоздко, но при этом работает как нужно. Целых 6 транзисторов нам понадобилось, чтобы реализовать XOR.
Что дальше
Теперь мы знаем, как можно комбинировать логические операции, используя транзисторы, чтобы получать то, что вам нужно. В следующий попрактикуемся и соберём целую схему, которая будет делать что-то полезное.












