Что мы уже знаем о транзисторах:
- Это устройство, похожее на кран, только для электричества, и он либо пропускает сквозь себя ток, либо не пропускает.
- Если такие «краны» правильно соединить, то можно создать иллюзию полезной для человека работы — например, суммирования.
- На транзисторах основаны все современные компьютерные вычисления. Современные транзисторы очень маленькие — в буквальном смысле микроскопические. Они соединены сложным образом внутри всех наших процессоров, контроллеров и даже памяти.
- Транзисторы сами по себе ничего не понимают. Они просто перемешивают электричество. Но если их правильно соединить и их будет много, от этого перемешивания получится значительная польза, от автоматических и очень быстрых математических операций до современных компьютеров.
В этой статье разберём, как же именно соединены транзисторы, чтобы уметь так хорошо считать. Для этого нужно сначала понять транзисторную логику, после чего станет очевидно, как устроена транзисторная математика.
Нам потребуется вспомнить эту картинку, которая обозначает принцип действия транзистора:
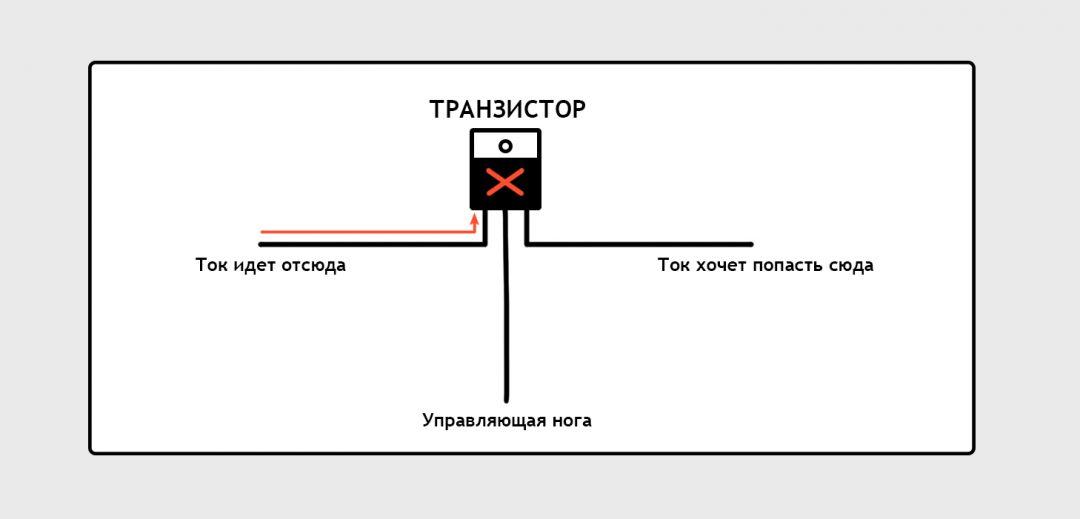
Тут ток течёт слева направо. На транзистор подаётся управляющий ток, который этот транзистор «открывает», и ток течёт. Если управляющий ток выключить, то транзистор «закроется», движение тока остановится.
Транзисторная логика
У транзисторов есть три принципиальных способа соединения, которые соответствуют трём базовым логическим операциям. Если понимать эти способы и логику, вы поймёте архитектуру всего компьютерного мира. Запоминать и учить её не надо, достаточно просто увидеть.
Основных логических операций всего три: И, ИЛИ, НЕ. Все остальные получаются из их комбинаций, поэтому нам достаточно понять, как работают эти. Можно представить, что мы через транзисторы хотим включить лампочку в комнате и у нас есть выключатель на стене.
Операция «НЕ»
Самая простая операция: она меняет значение на противоположное. Так как в компьютерах и транзисторах на базовом уровне существуют только понятия «есть ток» и «нет тока», то тут будет очевидно, что противоположно чему:
НЕ (есть ток) = нет тока
НЕ (нет тока) = есть ток
Эту же запись можно представить так:
НЕ (1) = 0
НЕ (0) = 1
В терминах нашей комнаты с лампочкой это звучит так: «Если выключатель выключен, то лампочка должна гореть». Схема подключения такая:
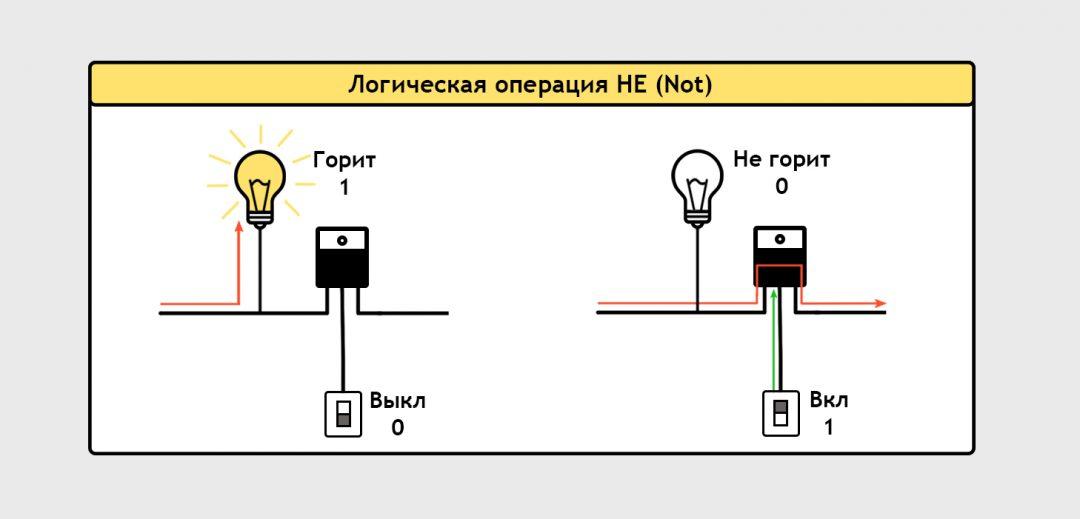
Инженеры договорились обозначать такую схему вот такой фигурой. Она означает «Логическая операция НЕ»:
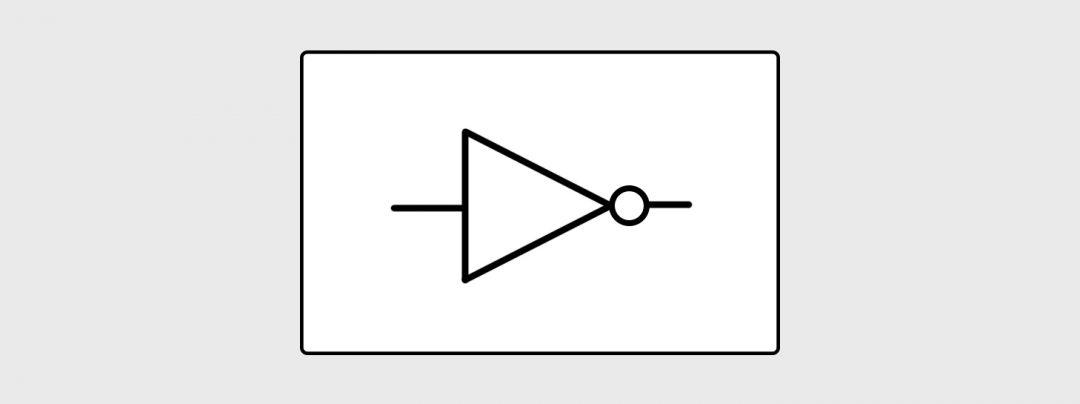
Операция «И»
Здесь уже участвуют два параметра, причём результат равен 1 только тогда, когда оба параметра — 1.
0 И 0 = 0
1 И 0 = 0
0 И 1 = 0
1 И 1 = 1
Только в последнем случае у нас получилась единица, потому что оба параметра — единицы. Как только хотя бы один из параметров — ноль, то всё выражение становится равно 0.
Это то же самое, как если бы у нас в комнате было два выключателя, а лампочка загоралась бы только тогда, когда включены оба.
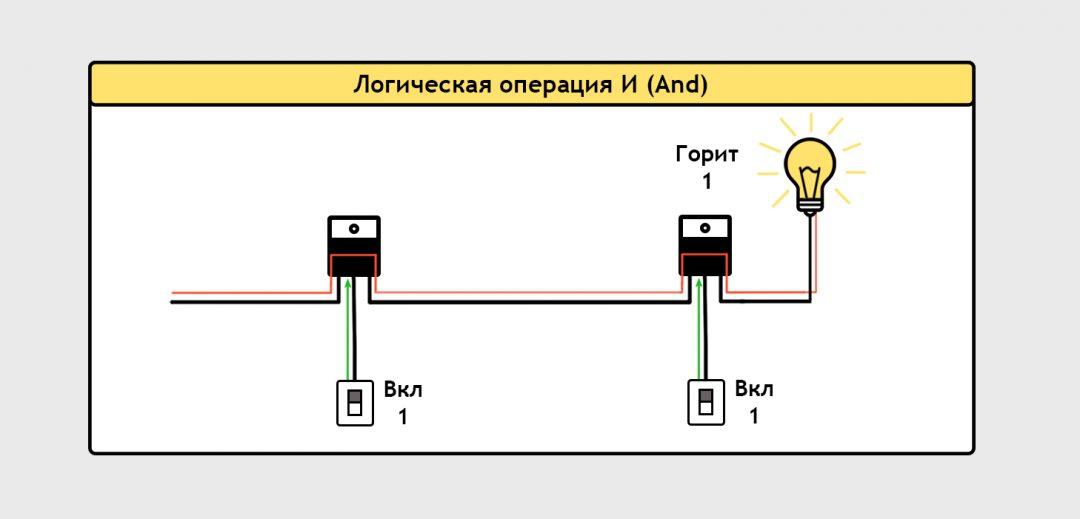
На схемах такой логический элемент обозначается так, два входа и один выход:
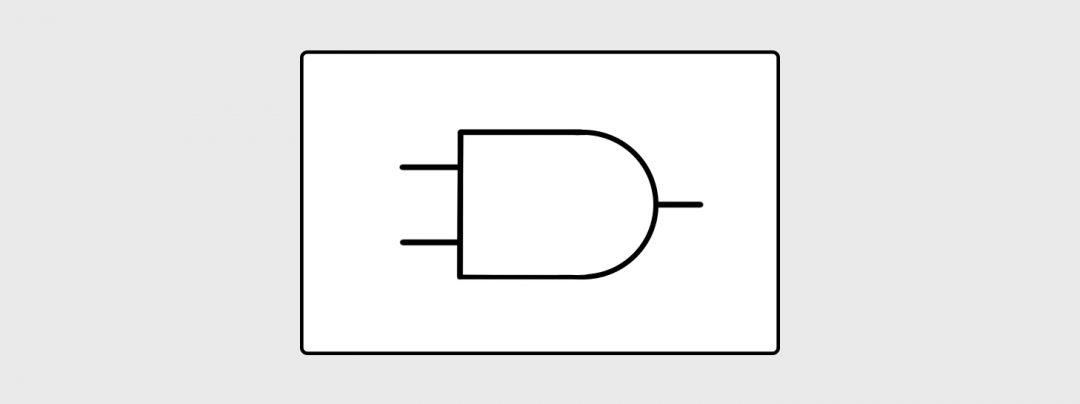
Операция «ИЛИ»
Тоже работает с двумя параметрами, но по другим правилам: если хотя бы одна единица есть, результат тоже будет единицей.
0 ИЛИ 0 = 0
1 ИЛИ 0 = 1
0 ИЛИ 1 = 1
1 ИЛИ 1 = 1
Эта операция смотрит, есть ли хоть одна единица, одна или вторая, или вообще обе, и если находит её — сразу тоже становится единицей.
В терминах комнаты с лампочкой: чтобы лампочка загорелась, должен быть включён хотя бы один выключатель.
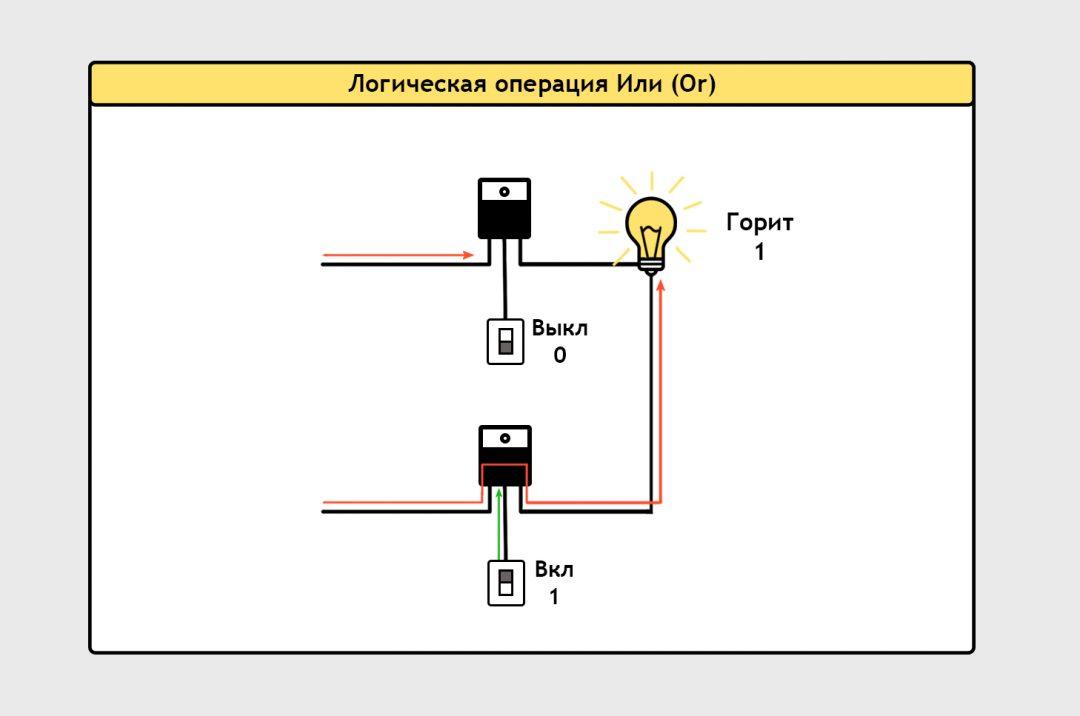
На схемах такой логический элемент обозначается так:
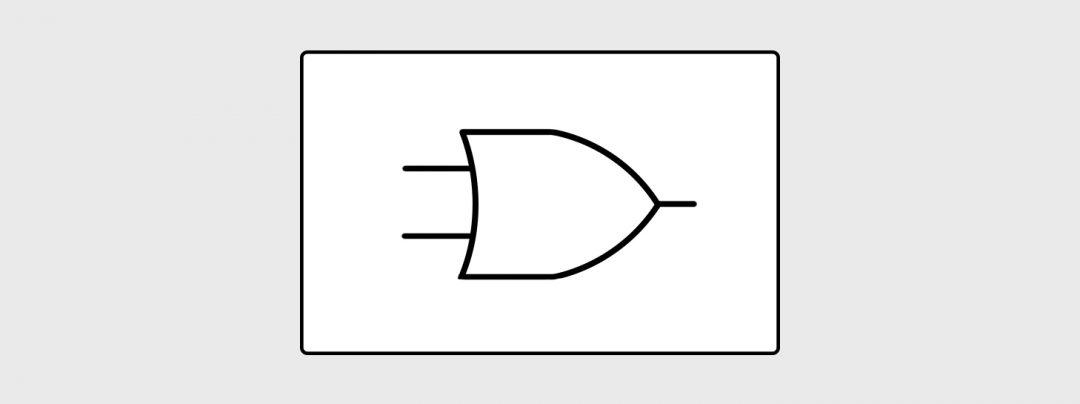
Вся логика и вычислительная мощь всех процессоров мира построена на этих трёх логических кубиках. Исключение — квантовые процессоры, но они устроены внутри совсем по-другому.
Что дальше
Комбинируя эти три логические схемы (там есть ещё четвёртая, она делается из трёх основных), мы сможем собрать такой каскад транзисторов, который поможет нам складывать числа. Забегая немного вперёд, вот каскад, который способен сложить два числа, если эти числа — единицы или ноли:
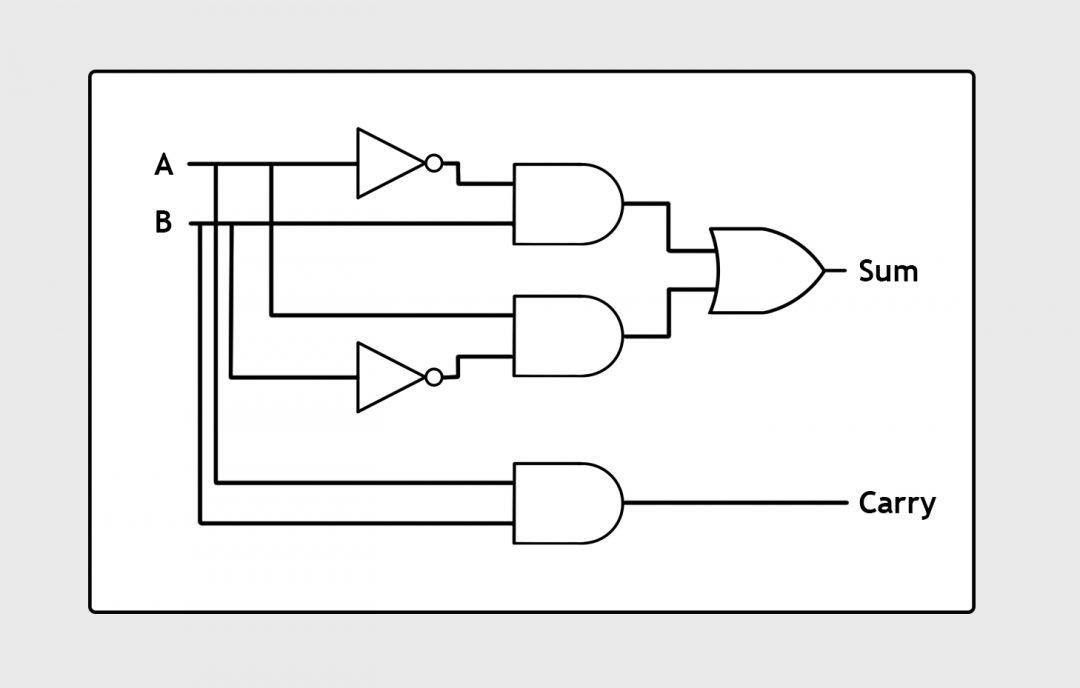
Этот каскад может сложить число размером 1 бит (единица или ноль). Его возможные результаты:
00 — ноль
01 — единица
10 — двойка в двоичном счислении
Если такой каскад «схлопнуть» до одной коробочки (и немного допилить), а потом соединить между собой несколько коробочек, можно складывать более сложные числа. Например, такой каскад сложит два числа до 4 бит, от 0 до 15:
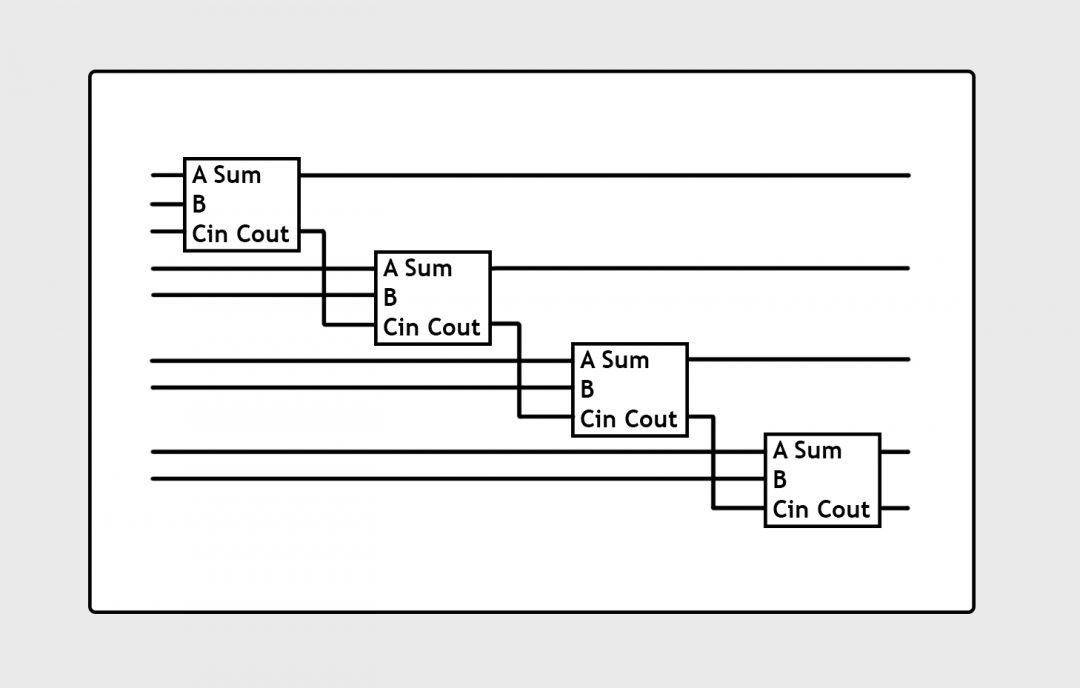
Что мы узнали на этом этапе.
- Транзисторы можно соединять по-разному: по цепочке, параллельно, как-то ещё хитро.
- В зависимости от схемы соединения эта конструкция из транзисторов будет давать разные результаты. Например, лампочка будет гореть при выключенном выключателе. Или будет гореть, когда включён хотя бы один. Или когда включены оба.
- Эти схемы соединений помогают воспроизвести простые логические операции: НЕ, И, ИЛИ.
- Из этих логических операций можно собрать простейший сумматор единицы и ноля.
- Из простейшего сумматора можно каскадом собрать более сложный, например, для чисел от 0 до 15.
- А дальше просто наслаиваешь эти сумматоры друг на друга, соединяешь разными хитрыми образами, и у тебя получается всё более и более сложная вычислительная машина.