Андрей, Вова и Саша — три друга-айтишника. Однажды летом они решили съездить из Москвы в город Мышкин Ярославской области: там красиво и как раз проходит выставка компьютерных мышей. Ехать на поезде не хотелось, а из транспорта у них был только двухместный мопед. Но ребята молодые и спортивные и задумали план: один пойдёт пешком, а двое поедут. Стартовать из Москвы решили одновременно. За какое самое короткое время все трое доберутся до Мышкина?
Немного цифр:
- Скорость пешком — 15 км/ч.
- Скорость мопеда — 60 км/ч.
- От Москвы до Мышкина — 300 км.
Начнём с самого очевидного решения. Пусть Андрей и Вова поедут на мопеде, а Саша идёт пешком. Когда Андрей с Вовой доберутся до Мышкина, Андрей оставит там Вову и поедет обратно, в сторону Москвы, чтобы забрать Сашу:
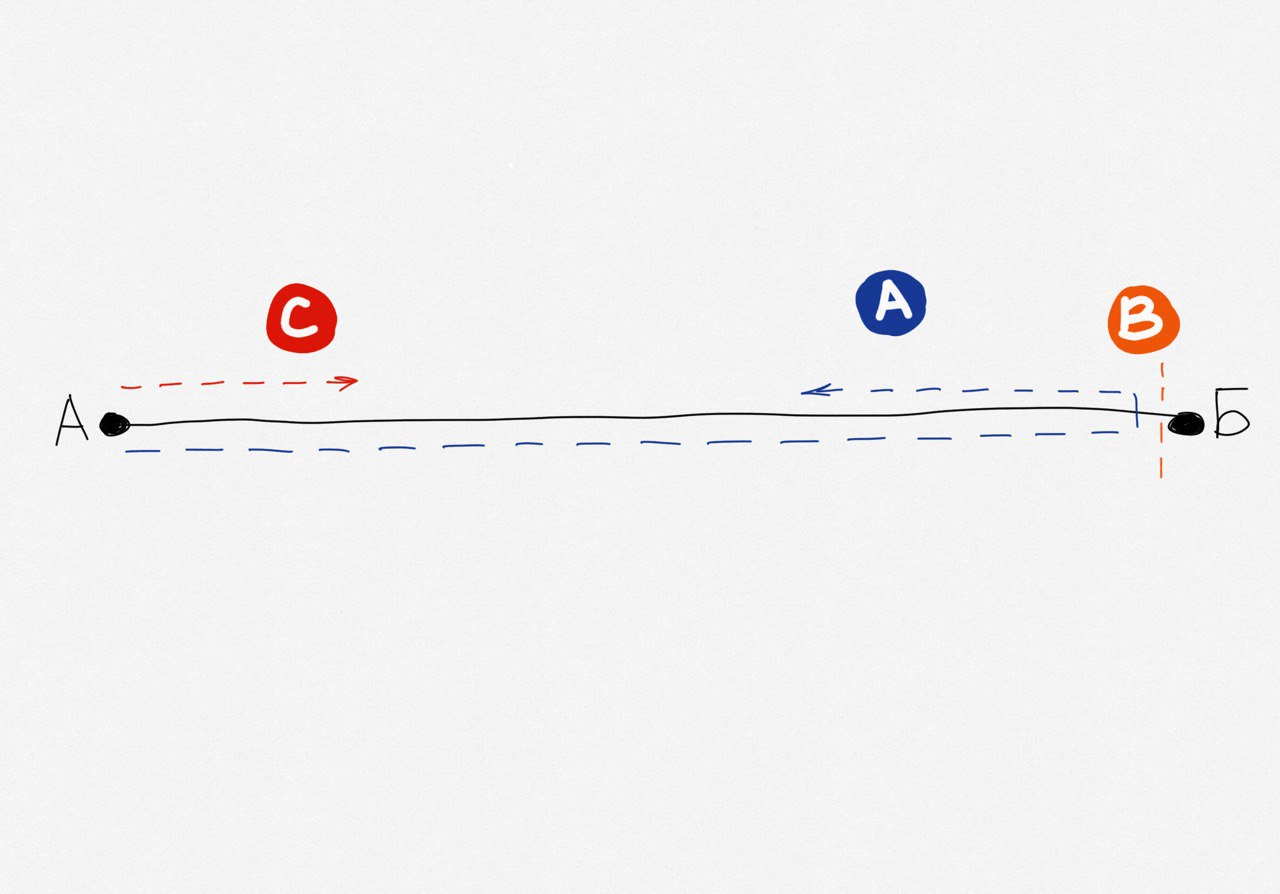
Это решение не самое оптимальное: пока Вова будет дожидаться Андрея с Сашей, он будет зря терять время и не внесёт никакого вклада в сокращение общего времени на дорогу. И если кто-либо из ребят будет ждать остальных, общее время не будет самым коротким.
Чтобы Вова мог поучаствовать в оптимизации времени, Андрею нужно оставить его недалеко от Мышкина. Тогда оставшееся расстояние Вова преодолеет пешком:
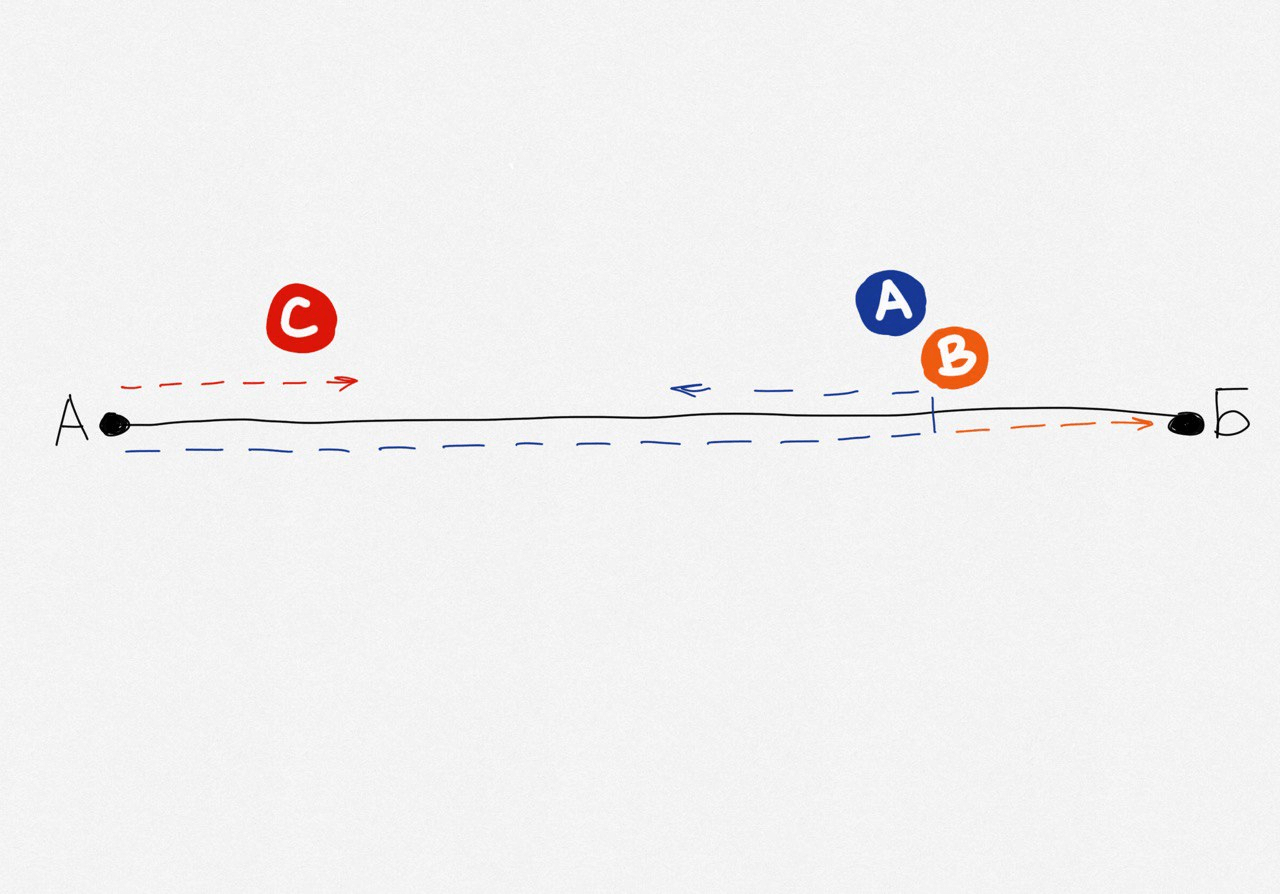
Как мы помним, общее время на дорогу может считаться самым коротким, если никто никого не дожидается. Если Вова доберётся раньше, он будет ждать Андрея с Сашей, а если позже, то Андрей и Саша будут ждать Вову.
Значит, нужно сделать так, чтобы Андрей с Сашей добрались до Мышкина одновременно с Вовой. Для этого нужно точно рассчитать точку на общем пути, где Андрей оставит Вову:
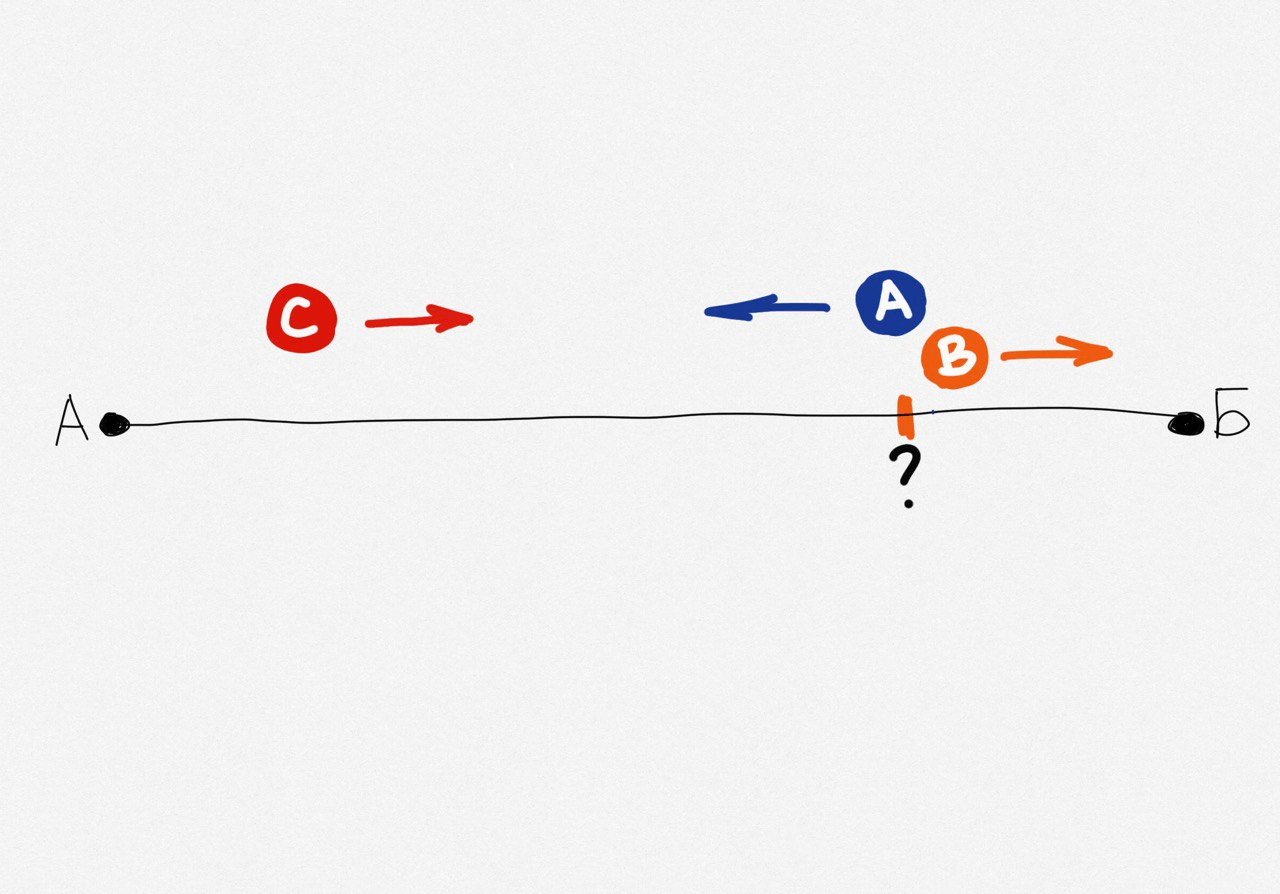
Теперь визуализируем весь план передвижений. Возьмём за А точку старта, за Б — точку финиша. В точке В1 Андрей оставит Вову. В это время Саша будет в точке С1. В точке С2 его подберёт Андрей, а Вова в этот момент достигнет точки В2:
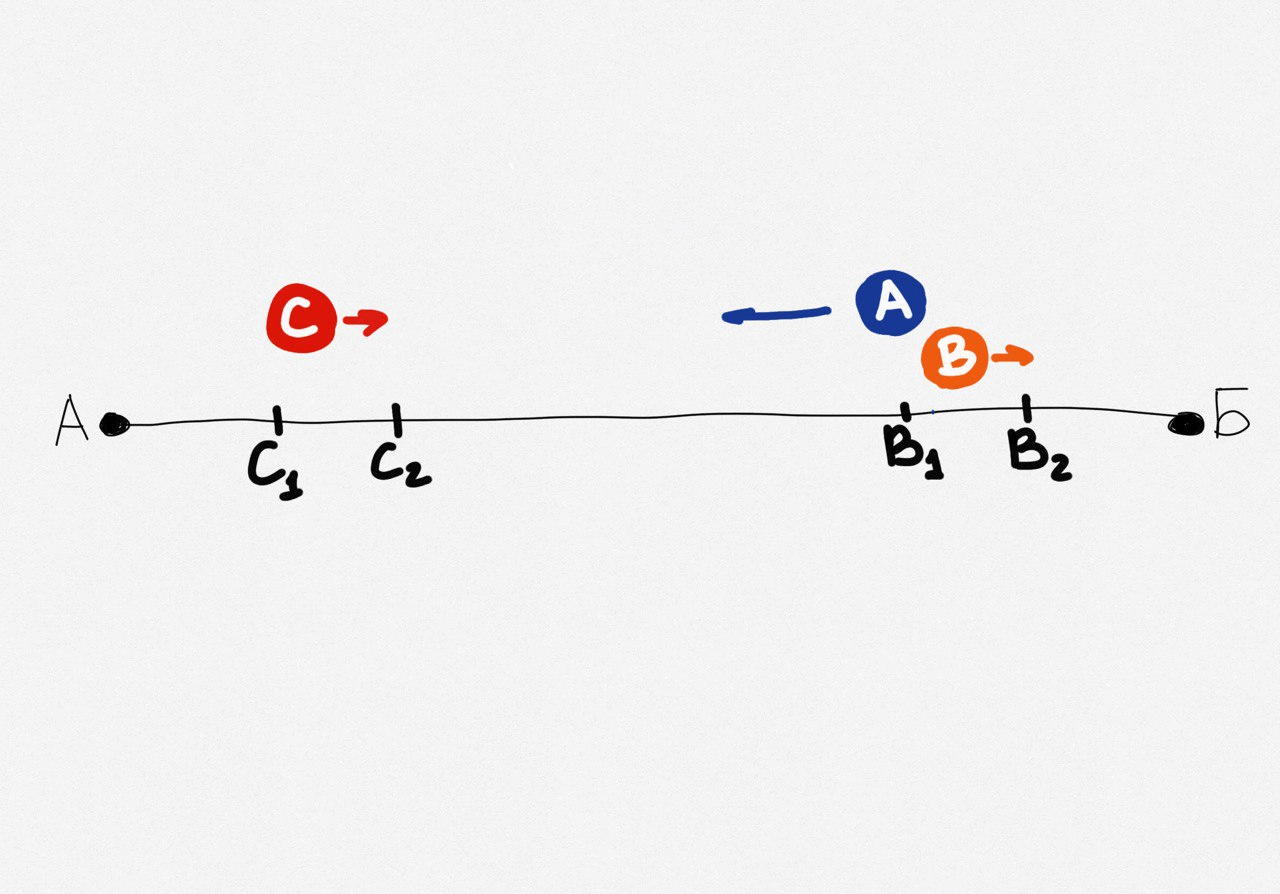
Теперь возьмём за t время, за которое Андрей вернётся на мопеде из точки В1 на точку С2, а расстояние от В1 до С2 возьмём за р:
t = В1С2/60 = р/60
За такое же время t Саша дойдёт из точки С1 до точки С2 (расстояние между ними возьмём за п):
t = С1С2/15 = п/15
За это же время t Вова дойдёт от точки В1 до В2:
t = В1В2/15
Так как в двух последних уравнениях у нас одинаковое время t и одинаковая скорость 15 км/ч, получается, что расстояние от С1 до С2 и от В1 до В2 — одинаковое:
t = п/15
Теперь на основании равенства времени t сравним расстояния р и п:
п/15 = р/60
р = 4п
Получаются такие отрезки:
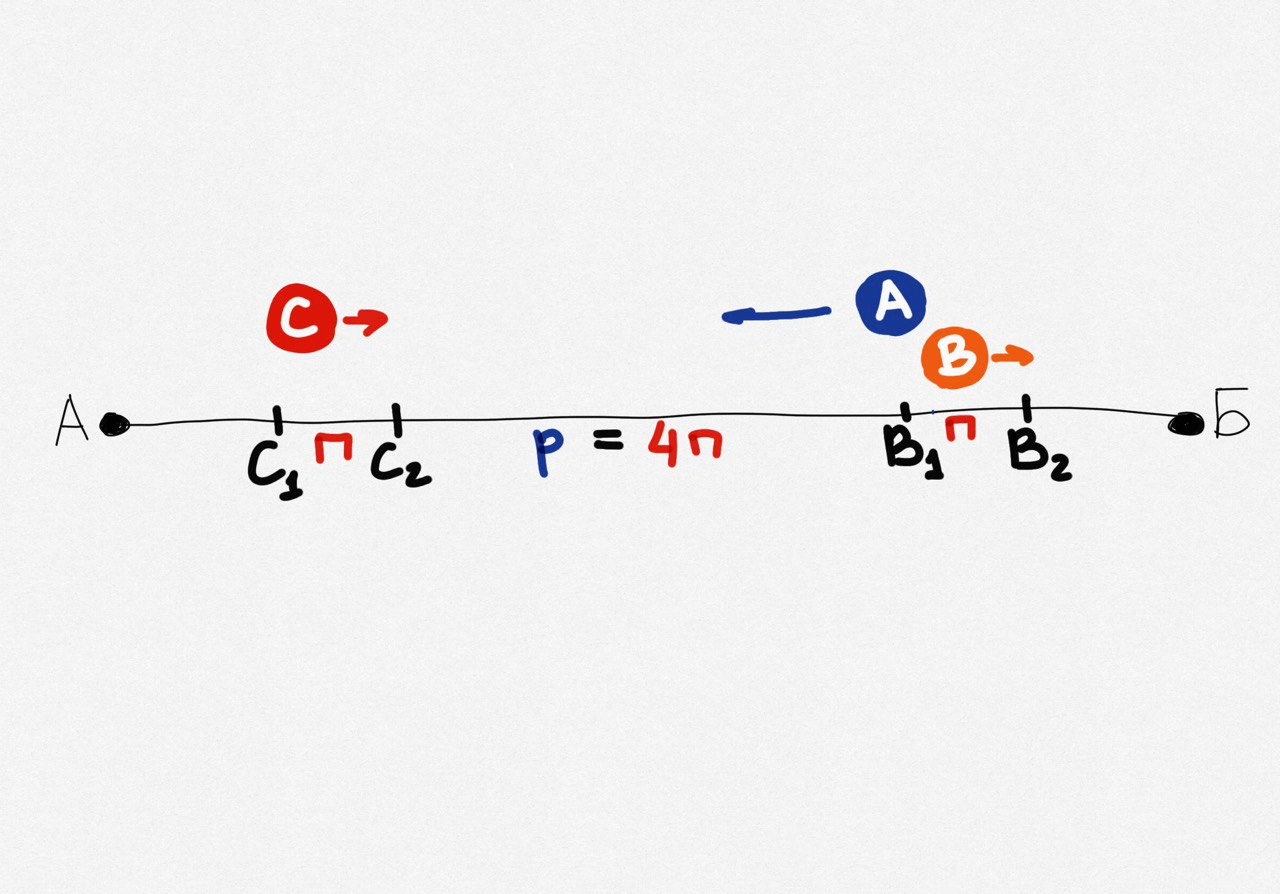
Теперь рассчитаем расстояние о, которое Вове останется пройти из точки В2 до Б. Время, за которое Андрей и Саша проедут расстояние 4п + п + о, будет равно времени, за которое Вова дойдёт расстояние о:
(4п + п + о)/60 = о/15
о = (5/3)п
Теперь наш план перемещений выглядит так:
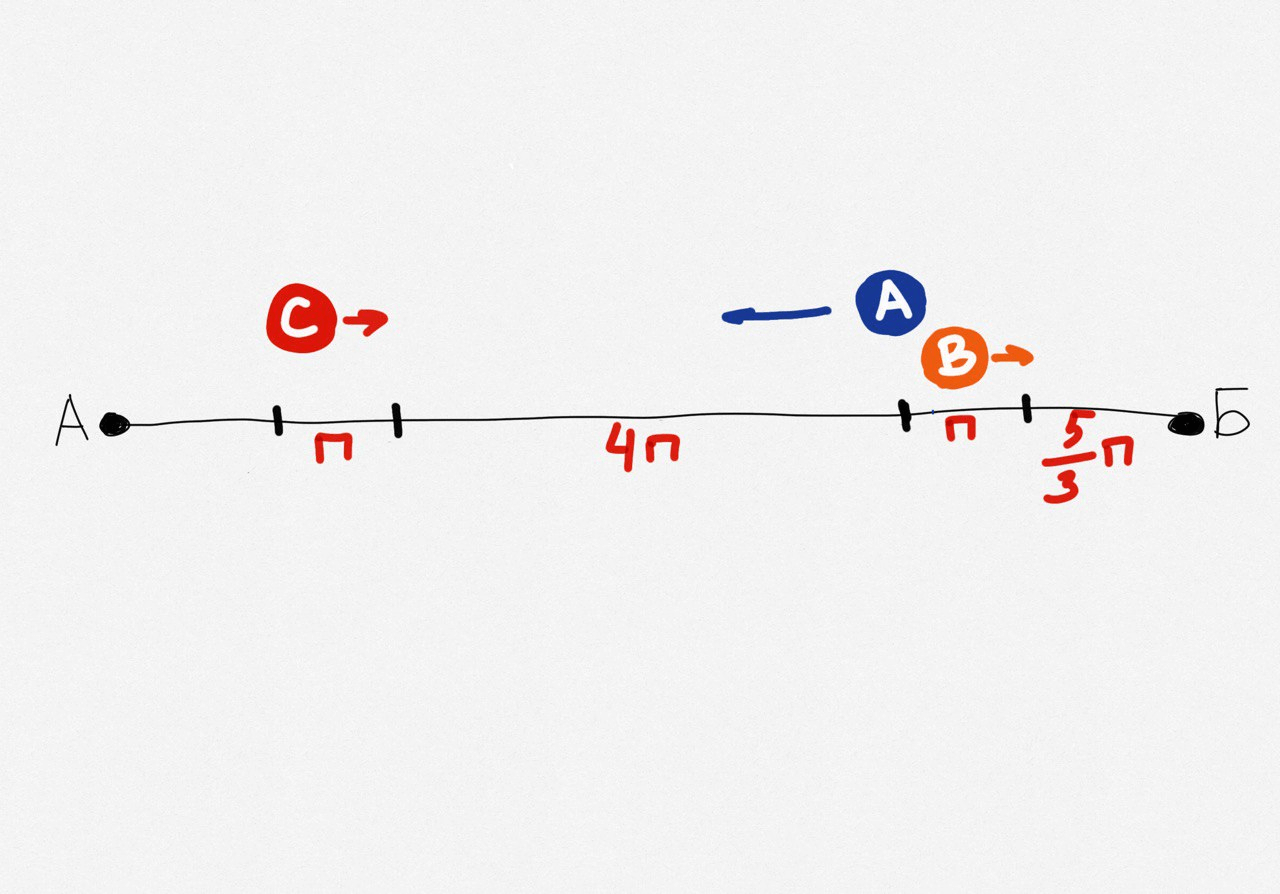
Нам осталось рассчитать расстояние н от точки старта А до С1. У нас снова получается равенство времени, за которое Саша дойдёт до точки C1, а Андрей с Вовой — доедут до точки В1:
н/15 = (н + п + 4п)/60
н = (5/3)п
Ещё раз визуализируем все пути:
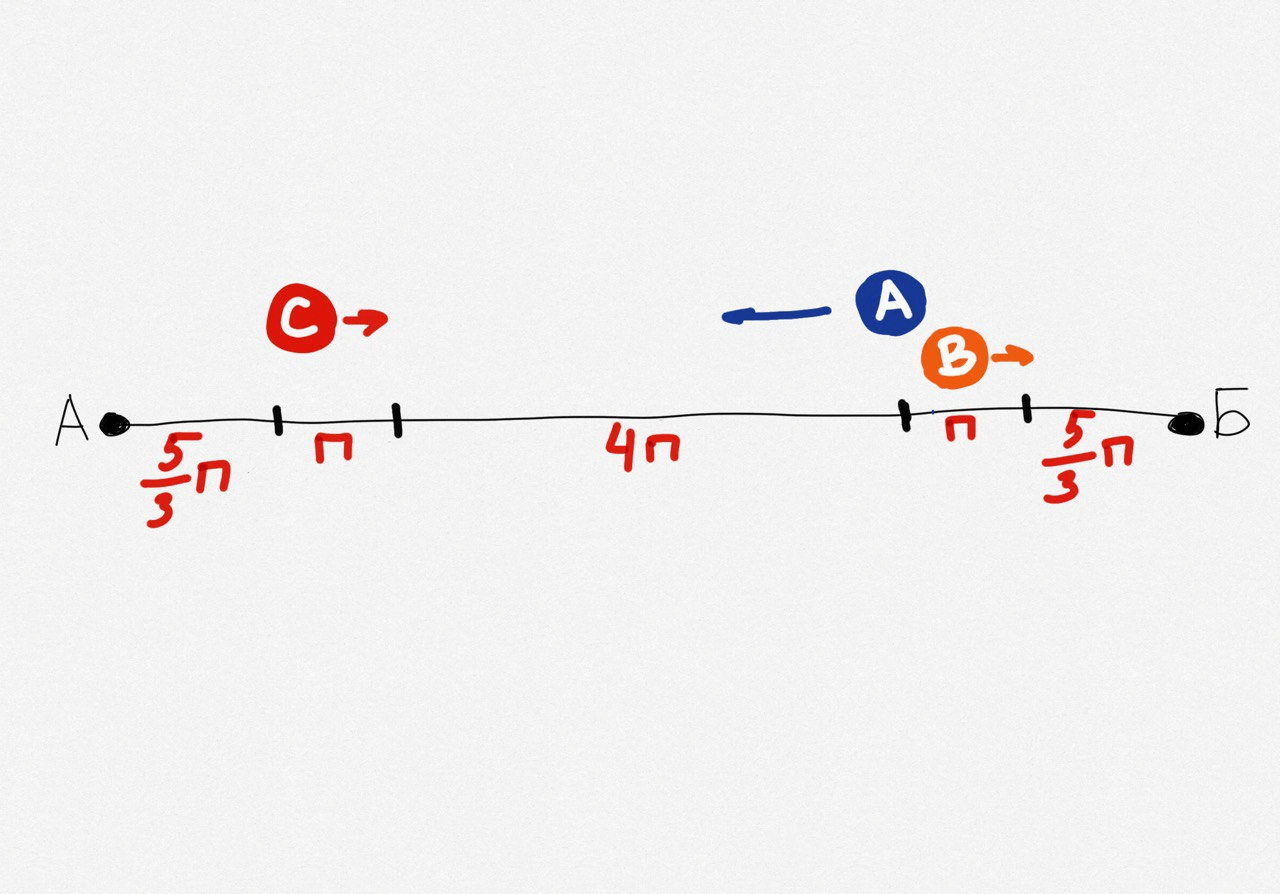
Получается такое равенство:
(5/3)п + п + 4п + п + (5/3)п = 300 км
п = 32,14 км
Подставим это значение в нашу визуализацию:
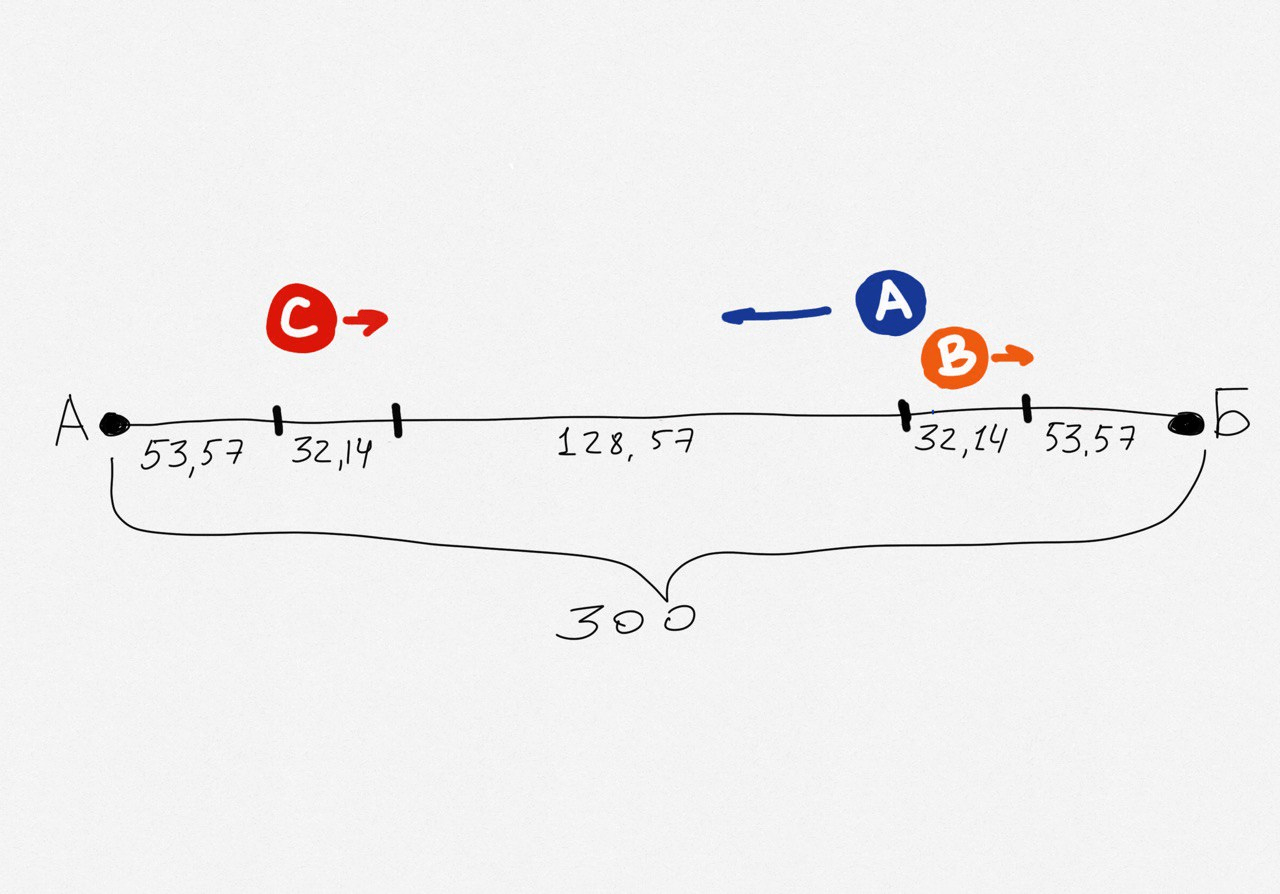
Теперь посчитаем самое короткое время, за которое все три айтишника доберутся из точки старта А до точки финиша Б. Посчитаем на примере Вовы:
t(Вова) = t(АВ1) + t(о)
t(Вова) = АВ1/60 + о/15
t(Вова) = 214,28/60 + 85,71/15
t(Вова) = 9,28 часа = 9 часов 17 минут
Получается, что самое короткое время составит примерно 9 часов, 17 минут.
















