Под занавес года угорели и нашли для вас последнюю задачку. Кто её решит — тому Дед Мороз под ёлочку что-нибудь этсамое.
Если бы здесь было про 2022-й и 2023-й, было бы красивее, но эта задача такая какая есть.
Задача такая: найти все целые решения этих уравнений:
 Школьная загадка про сейф, которая ставит в тупик большинство взрослых
Школьная загадка про сейф, которая ставит в тупик большинство взрослых Школьная задача, которую дети решают без калькулятора, а взрослые — нет
Школьная задача, которую дети решают без калькулятора, а взрослые — нет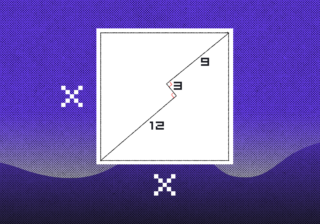 Непростая задача про диагональ квадрата
Непростая задача про диагональ квадрата Задачка, после которой вы полюбите факториал!
Задачка, после которой вы полюбите факториал! Задача про команду программистов, тимлида и таск-трекер
Задача про команду программистов, тимлида и таск-трекер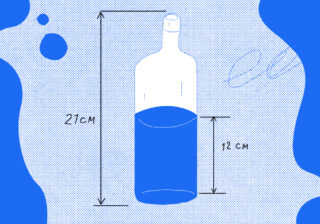 Сколько воды в бутылке?
Сколько воды в бутылке?ab + c = 2020
a + bc = 2021
При всей кажущейся простоте у этой задачи довольно длинное решение.
Первым делом объединим два уравнения и перенесём все неизвестные в одну сторону, а числа — в другую:
a + bc − (ab + c) = 2021 − 2020
a + bc − ab − c = 1
Поменяем местами второе и третье слагаемое:
a − ab + bc − c = 1
Вынесем общее за скобки:
a (1 − b) + c (b − 1) = 1
Во второй скобке у нас то же самое, что и в первой, только с противоположными знаками. Чтобы их снова поменять местами, вынесем −1 из второй скобки — так у нас плюс превратится в минус:
a (1 − b) − c (1 − b) = 1 ← тут тоже вынесем общее в отдельную часть
(1 − b) × (a − c) = 1
Теперь не самое очевидное. В решении нас просят найти только целые числа. У нас перемножение. Какие числа при перемножении дают единицу? Давайте думать:
1 × 1 = 1
−1 × −1 = 1
Всё, больше никаких вариантов перемножения у нас не может быть. Это значит, что обе наших скобки одновременно равны или единице, или минус единице. Проверим каждый вариант.
Допустим, обе скобки равны единице. Это значит, что:
1 − b = 1
a − c = 1
Из первого уравнения видно, что b = 1 − 1 = 0. Подставляем это значение в самое первое наше выражение:
ab + c = 2020
a × 0 + c = 2020 → c = 2020
Если c = 2020, а a − c = 1, то a = 2020 + 1 = 2021. Проверим это, подставив все числа в исходные уравнения:
2021 × 0 + 2020 = 2020
2021 + 0 × 2020 = 2021
Всё сходится, значит, мы нашли первое решение: a = 2021, b = 0, c = 2020.
Допустим, обе скобки равны минус единице. Это значит, что:
1 − b = −1
a − c = −1
Из первого уравнения видно, что b = 1 + 1 = 2. Подставляем это значение в самое первое наше выражение:
2a + c = 2020
a + 2c = 2021
Умножим первое на два, обе части:
4a + 2c = 4040
Теперь в обоих уравнениях у нас есть 2c — используем это, чтобы вынести их в одну сторону, а потом приравнять то, что осталось, друг к другу:
2c = 4040 − 4a
2c = 2021 − a
4040 − 4a = 2021 − a → 4a − a = 4040 − 2021
3a = 2019 → a = 673
Подставим a во второе короткое выражение, чтобы найти c:
673 − с = −1 → с = 674
Проверим то, что получилось, подставив все числа в исходные уравнения:
673 × 2 + 674 = 2020
673 + 2 × 674 = 2021
Всё сходится, значит, мы нашли второе решение: a = 673, b = 2, c = 674.
Сложно? Сложно.
Зачем? Ради процесса.
Так выпьем же за то, чтобы процесс приносил удовольствие, а результаты сходились. С наступающим!