Перед вами очередная задачка с собеседований в крупные IT-компании. Вот сама задача:
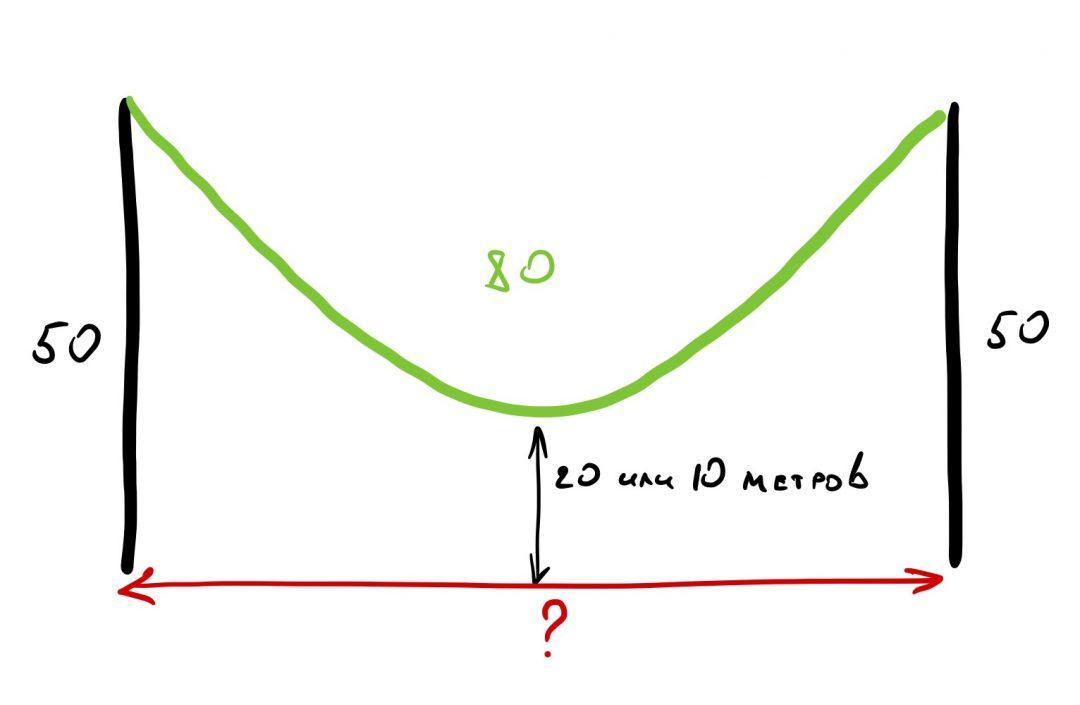
Кабель длиной 80 метров висит на двух столбах. Высота каждого столба — 50 метров. Каково расстояние между столбами, если центр провисающего кабеля находится:
а) на высоте 20 метров от земли — вариант для технарей;
б) на высоте 10 метров от земли — вариант для гуманитариев.
Для решения можно использовать инженерный калькулятор с расширенными функциями.
В задаче нет никакого подвоха, но для решения нужно хорошо знать математику, углы и угловые функции. Сначала попробуйте решить её самостоятельно, а потом загляните в решения.
Первое, что мы сделаем, — поднимем уровень земли, чтобы он касался провода. Так как до центра провиса 20 метров, то высота столбов тоже уменьшится на эти 20 метров:
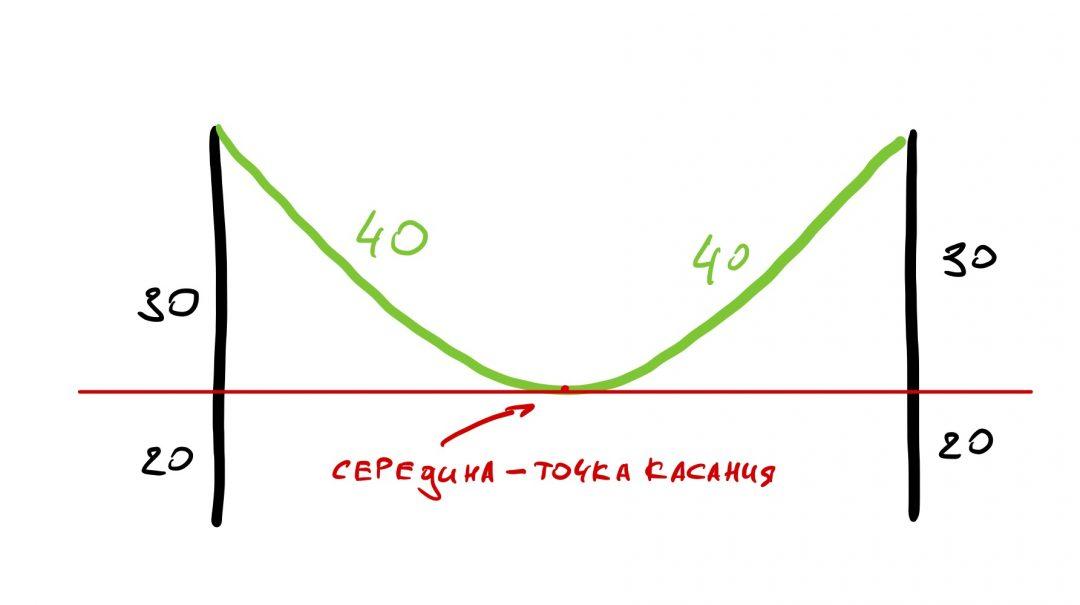
Расстояние между столбами у нас при этом осталось тем же самым.
Так как кабель провисает по центру, нам достаточно найти расстояние от края до середины и умножить его на 2 — так мы найдём полное расстояние между столбами.
❗️ Самая важная часть.
Так как провисающий кабель похож на параболу, то мы для решения будем использовать не тригонометрические функции, которые работают с прямыми и окружностями, а гиперболические.
Если нужно точно описание этих функций — вот оно:
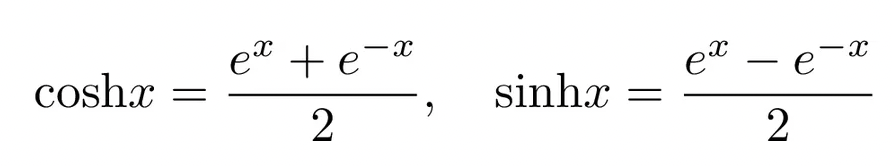
Сначала поработаем с высотой столба. Запишем формулу для расстояния, затем добавим на рисунок те данные, которые мы уже знаем, и раскроем формулу:
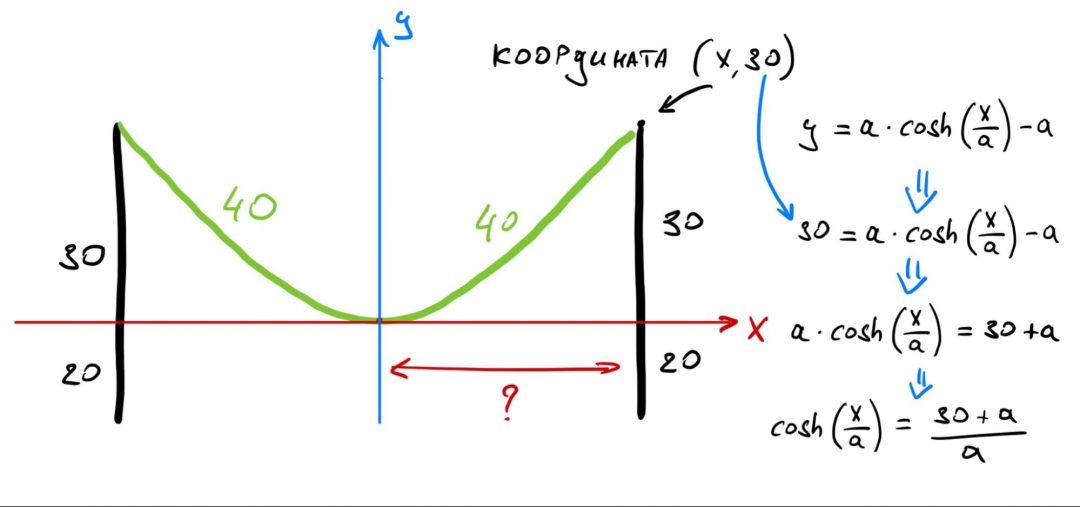
Теперь составим второе уравнение, в котором используем значение длины кабеля. Так как он провисает ровно посередине, то его длина от края до точки перегиба — 40 метров.
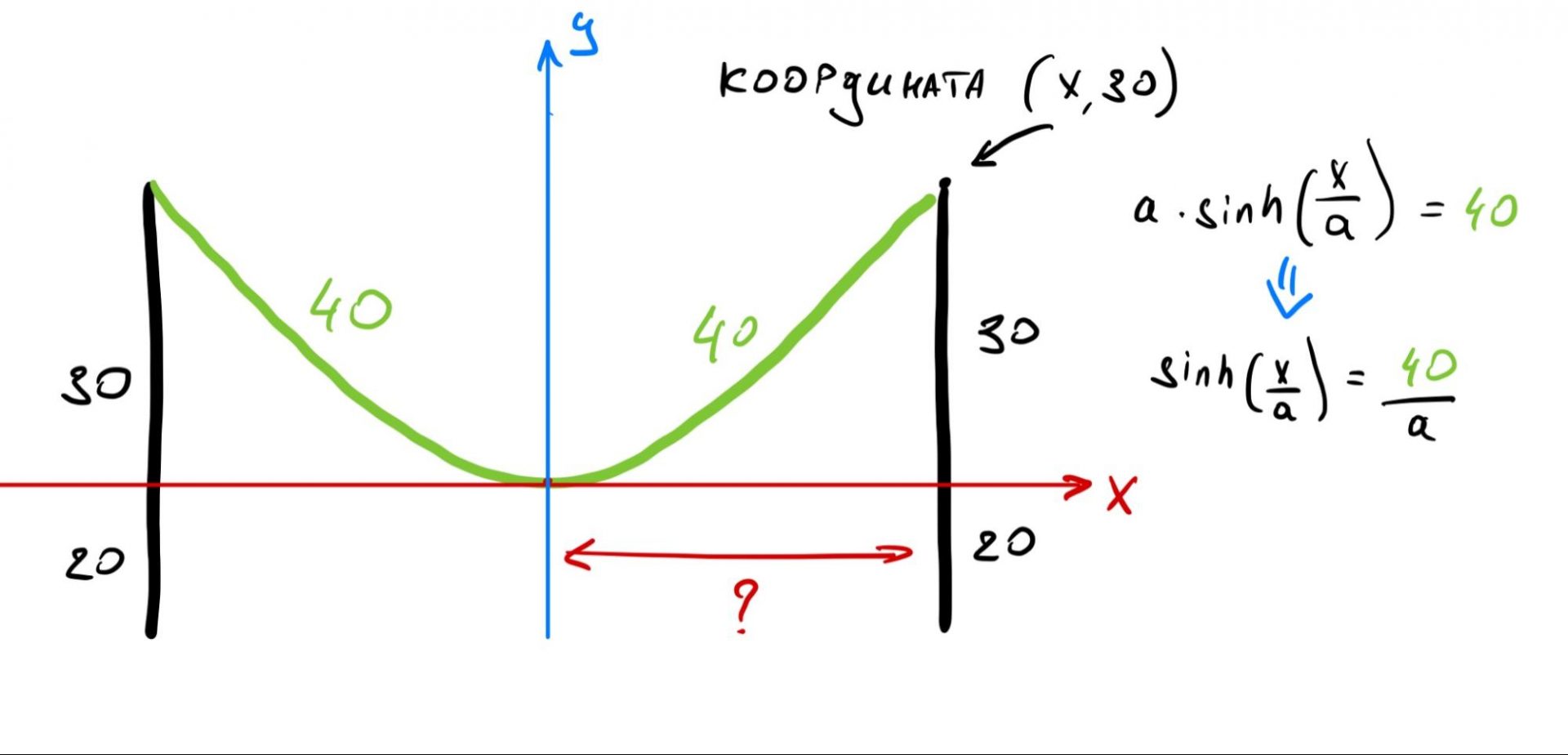
Добавляем свойство о том, что разность квадратов гиперболического синуса и косинуса равна единице:
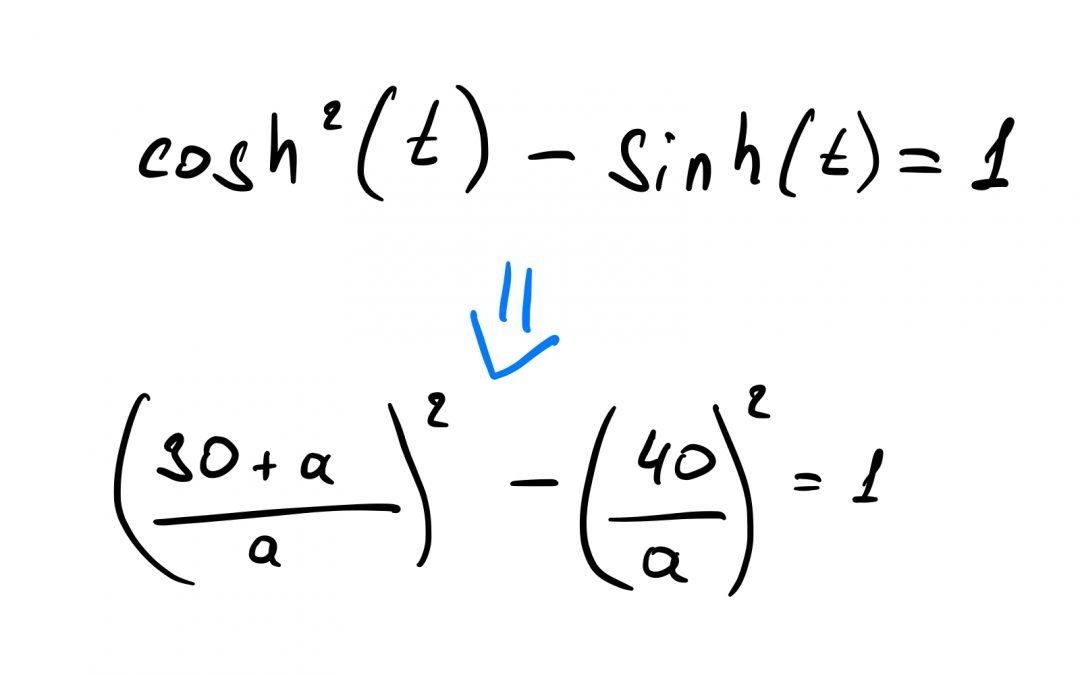
Раскрываем скобки, приводим всё к классическому квадратному уравнению, и, решая его, получаем ответ: a = 35/3.
Это значение подставляем в формулу гиперболического синуса, чтобы посчитать половину длины кабеля:
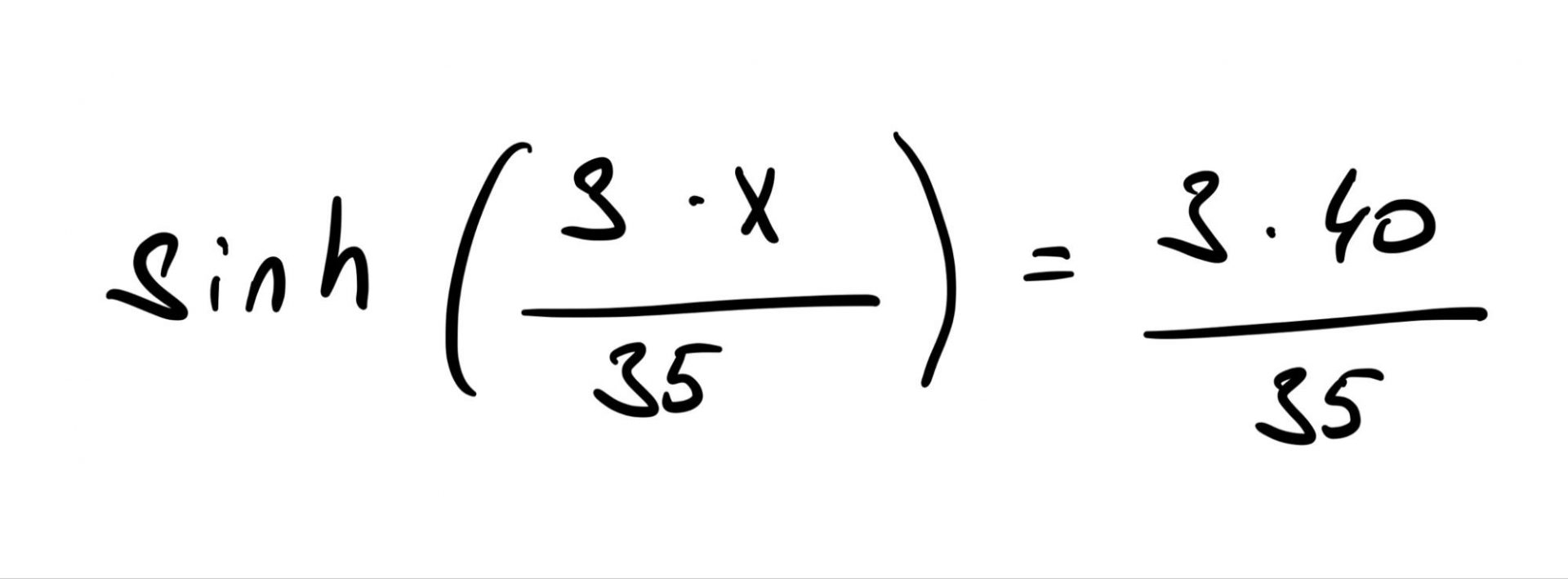
Решаем это уравнение на калькуляторе и получаем ответ: x ≈ 22,7. Это половина расстояния между столбами, а полное расстояние ≈ 45,4 метра.
Ответ: если высота до центра провиса равна 20 метров, то расстояние между столбами составляет примерно 45,4 метра.
У гуманитариев кабель длиной 80 метров провисает на минимальной высоте 10 метров от земли. При этом высота столба 50 метров. Значит, если провести новый «уровень земли» (красным), верхняя часть столба будет равняться 40 метрам.
Посмотрите на рисунок. Нет ли здесь ошибки?
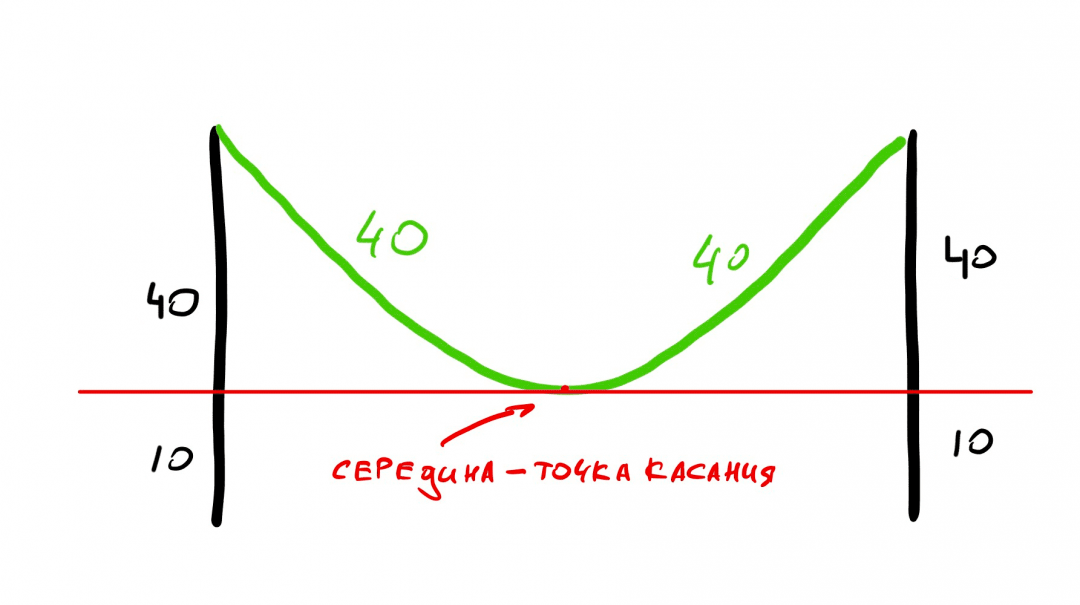
Если верхняя часть столба 40 метров и длина кабеля до середины — тоже 40 метров, то какой это треугольник? Может ли такой треугольник существовать?
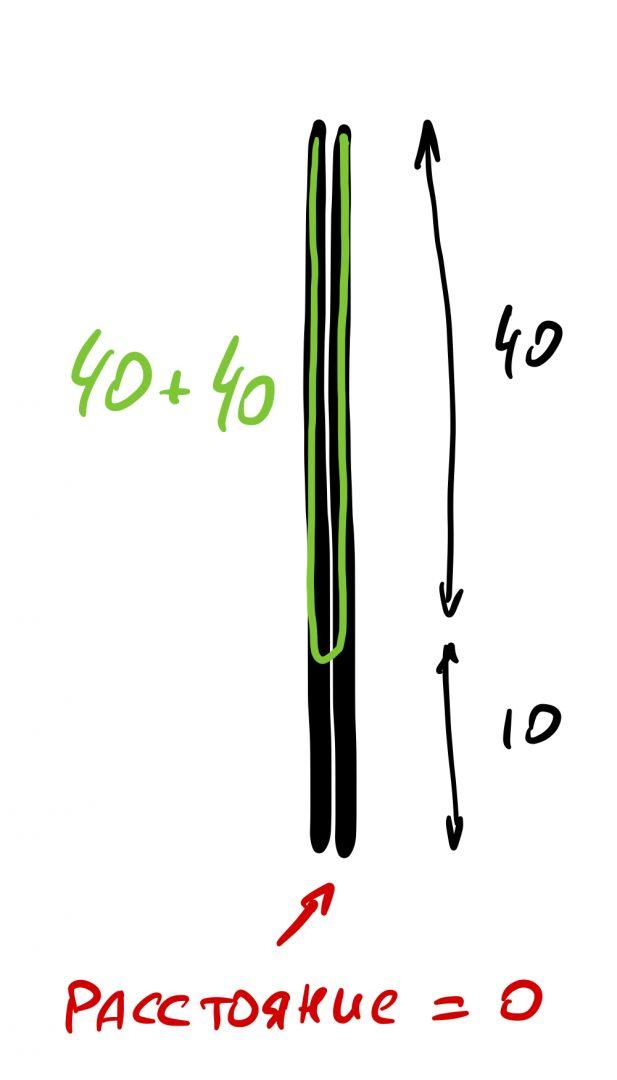
И в чём тут мораль, Код?
В смысле мораль? Это математическая задачка, зачем тут мораль?