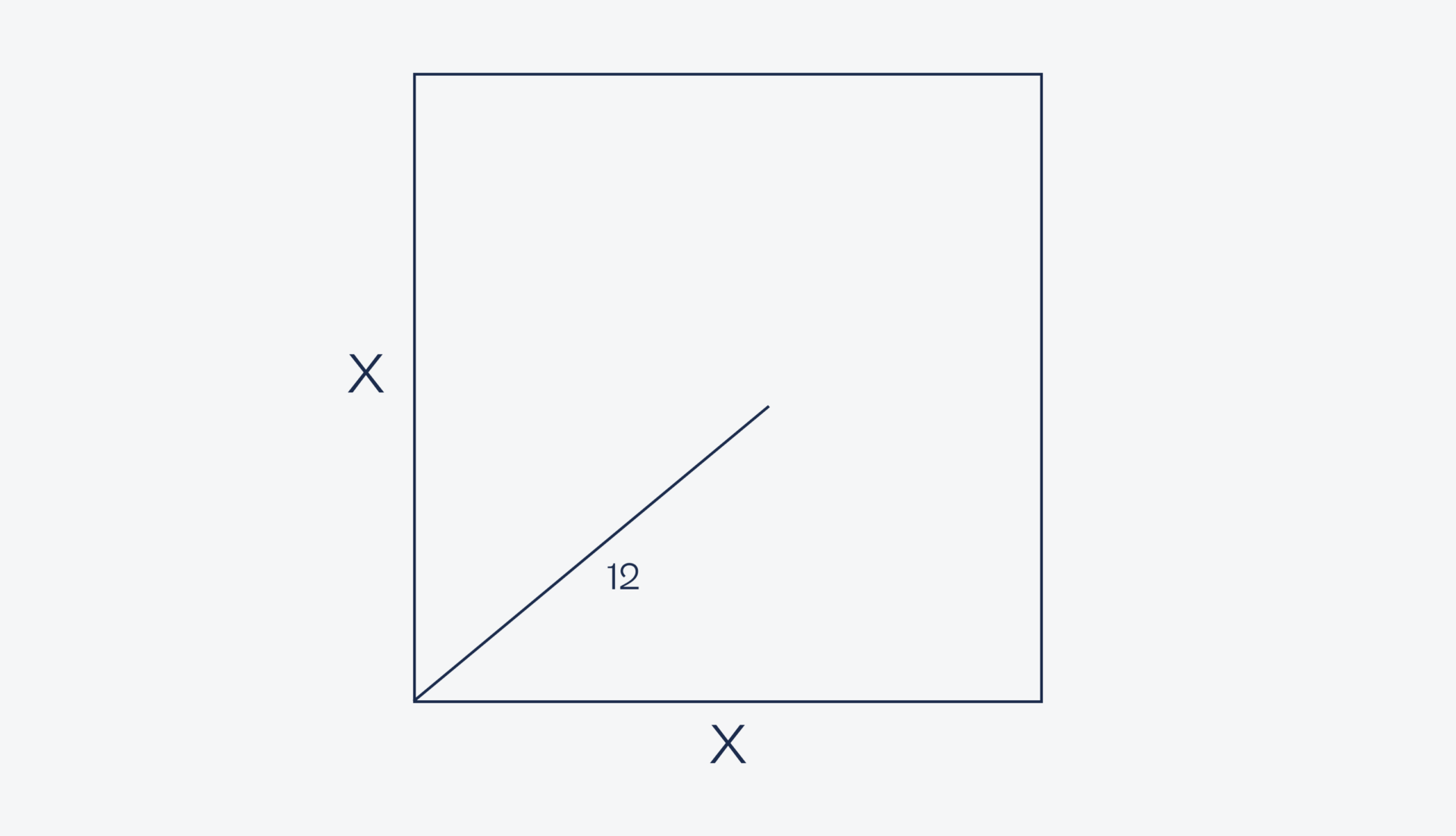
Если вы уже окончили школу, попробуйте решить эту задачку в уме, используя формулу длины диагонали квадрата:
d = X√2,
где X — это длина стороны квадрата.
 Школьная загадка про сейф, которая ставит в тупик большинство взрослых
Школьная загадка про сейф, которая ставит в тупик большинство взрослых Школьная задача, которую дети решают без калькулятора, а взрослые — нет
Школьная задача, которую дети решают без калькулятора, а взрослые — нет Нестандартная задача про наши счастливые годы: 2020-й и 2021-й
Нестандартная задача про наши счастливые годы: 2020-й и 2021-й Задачка, после которой вы полюбите факториал!
Задачка, после которой вы полюбите факториал! Задача про команду программистов, тимлида и таск-трекер
Задача про команду программистов, тимлида и таск-трекер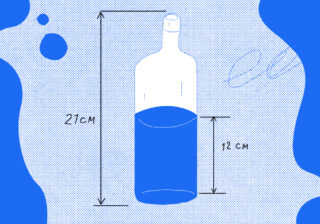 Сколько воды в бутылке?
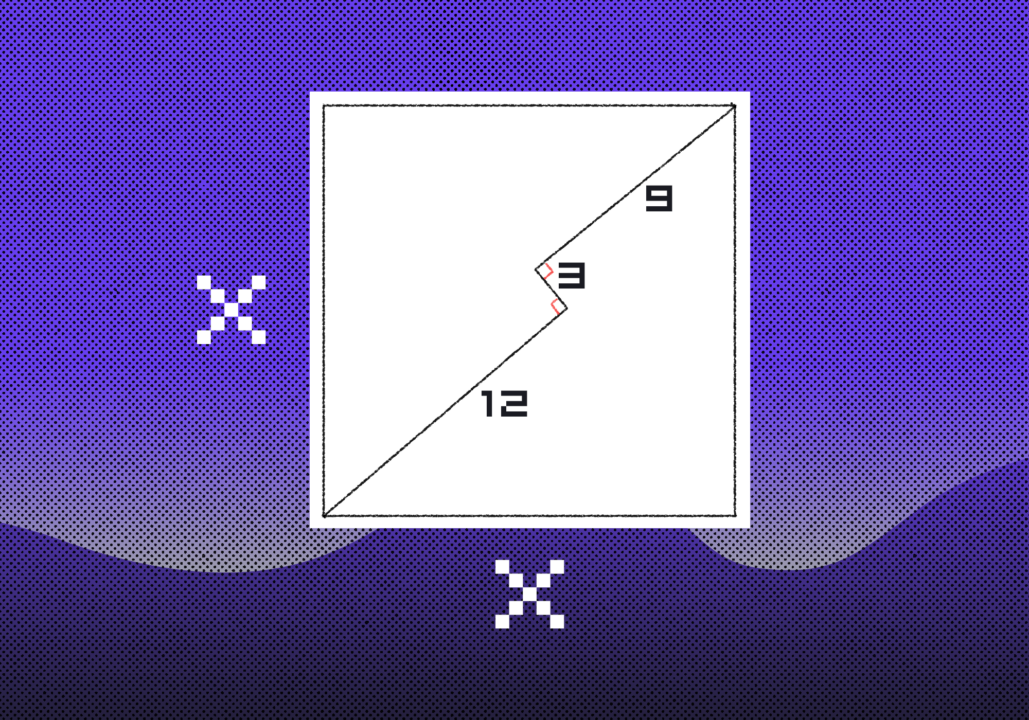
Сколько воды в бутылке?Теперь условия: есть квадрат с длиной стороны x. Из нижнего левого угла провели под каким-то углом линию длиной 12 сантиметров:
После этого повернули на 90 градусов и провели вторую линию длиной 3 сантиметра:
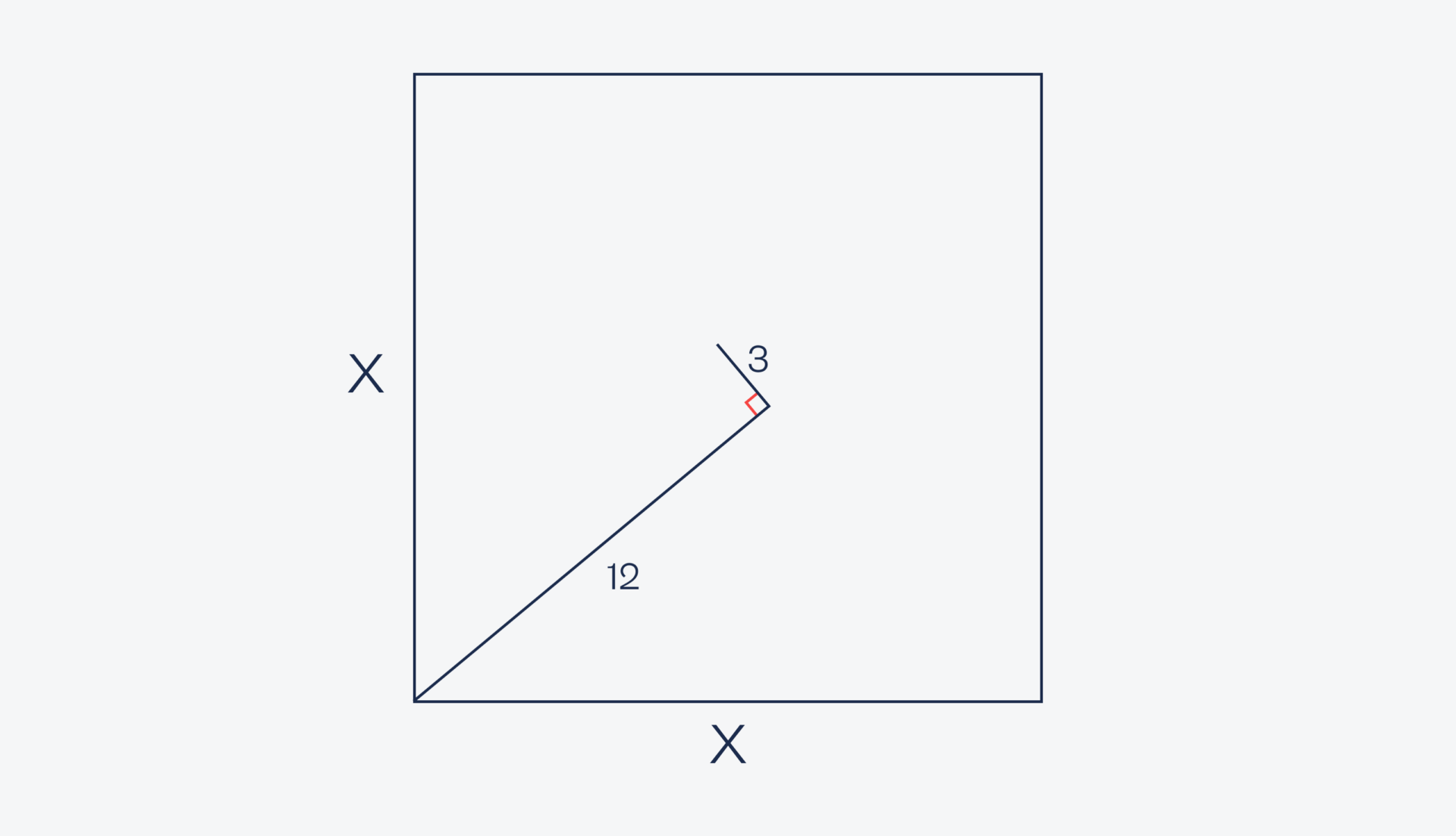
Нужно найти X, то есть длину стороны квадрата.
Чтобы найти решение, нам придётся выйти за рамки квадрата и использовать свойства перпендикулярных линий и прямых углов.
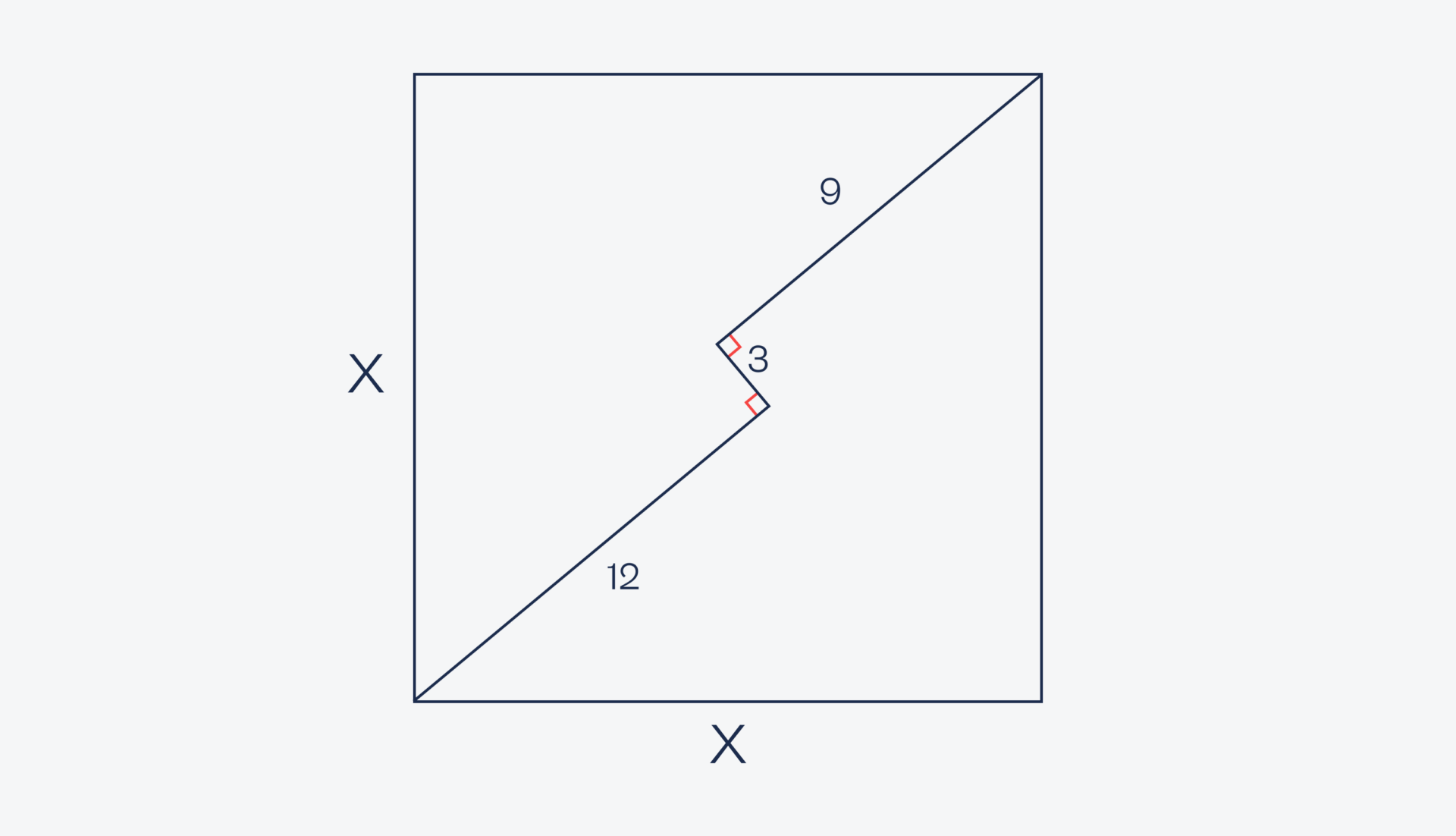
Возьмём два отрезка, 9 и 12 сантиметров, и на противоположных концах тоже под прямым углом построим отрезки по 3 сантиметра:
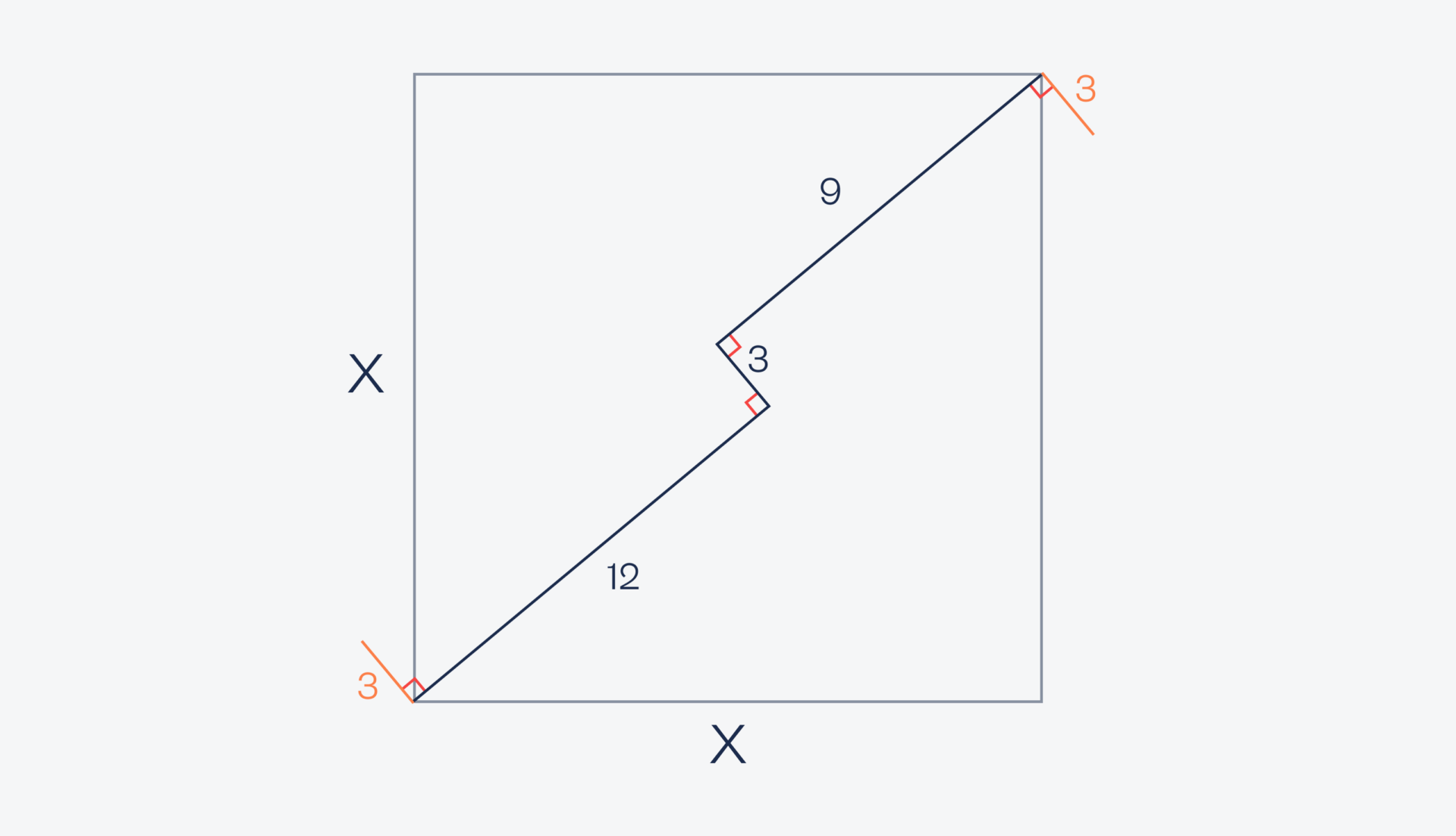
Теперь достроим недостающие линии в каждом прямоугольнике — 9 и 12 сантиметров — и тоже под прямым углом. Так как везде получились углы по 90 градусов, то перед нами два прямоугольника с общей стороной 3 сантиметра:
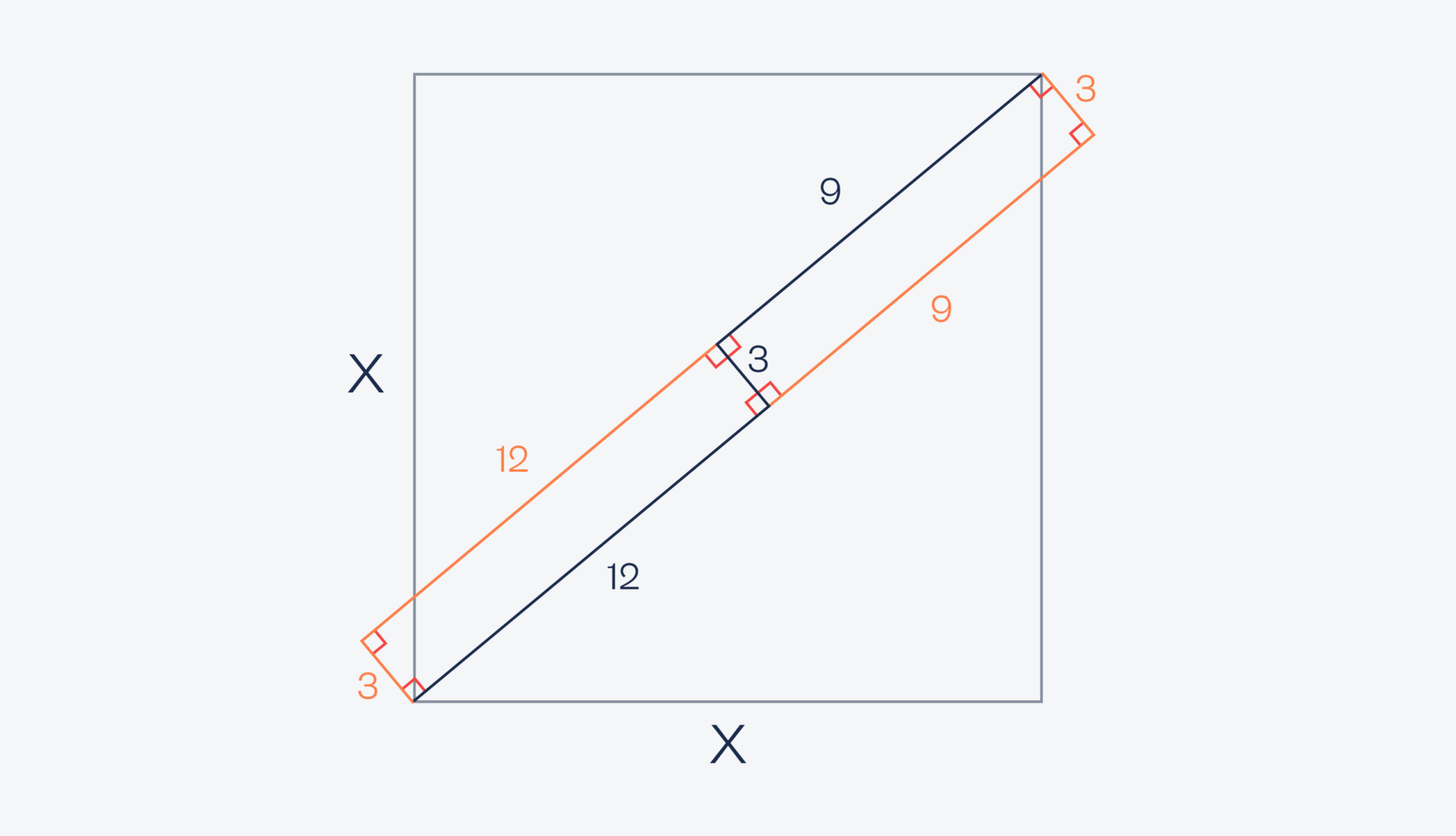
Если их объединить, то у нас получится прямоугольник длиной 9 + 12 = 21 сантиметр и шириной 3 сантиметра. Проведём диагональ в этом прямоугольнике:
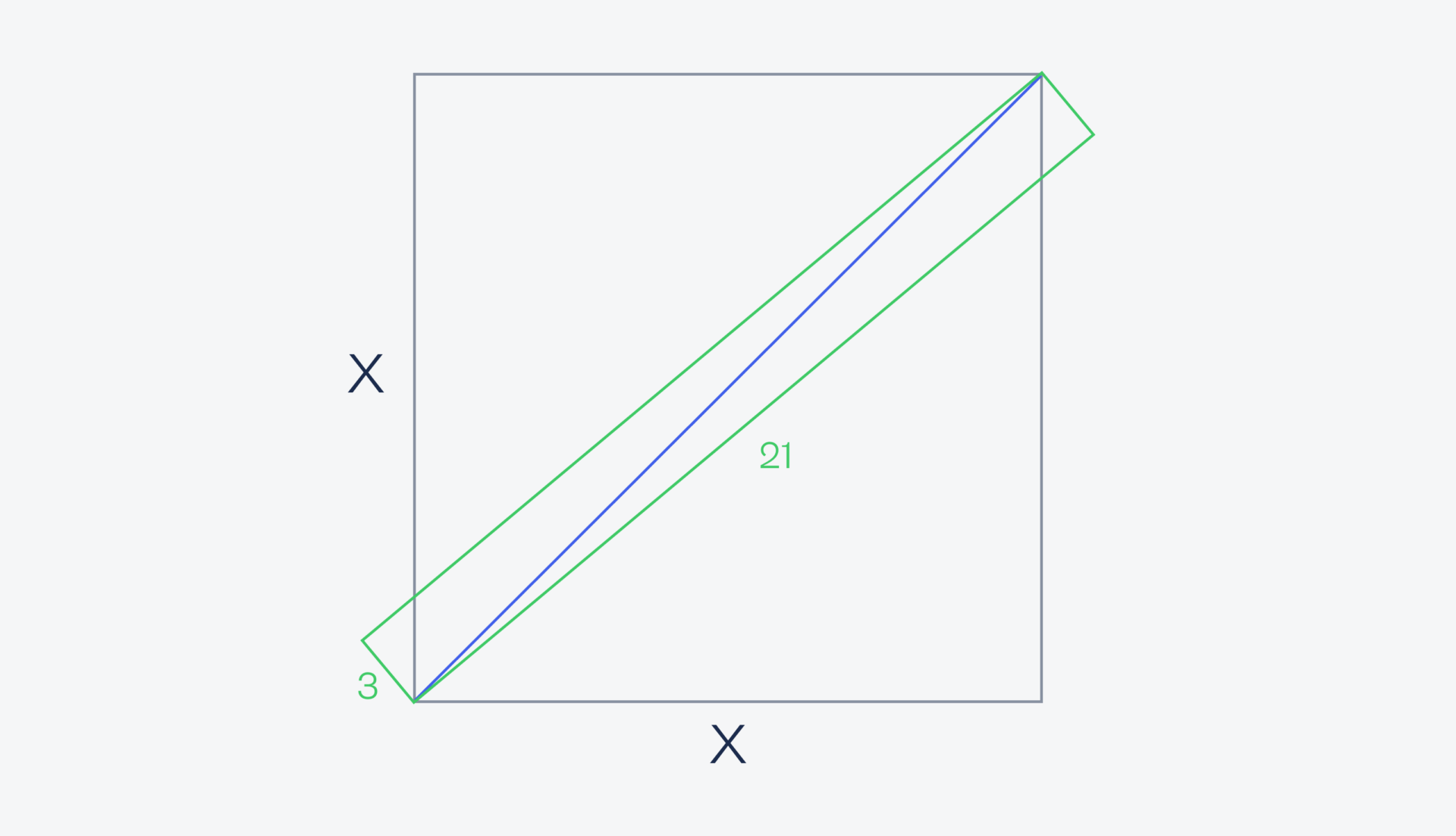
А теперь важное замечание: так как углы прямоугольника совпадают с углами квадрата, то диагональ прямоугольника — это диагональ квадрата и их длины равны. По теореме Пифагора a² + b² = c² найдём диагональ:
21² + 3² = с² → 441 + 9 = с² → с² = 450
с = √450 = 15√2
Тут нам пригодится формула длины диагонали квадрата: с = X√2. Но у нас c = 15√2, получается, что X = 15 — это и есть длина стороны квадрата.