Разберём свежую задачу с канала MindYourDecisions. Это не про программирование, но развивает логическое мышление.
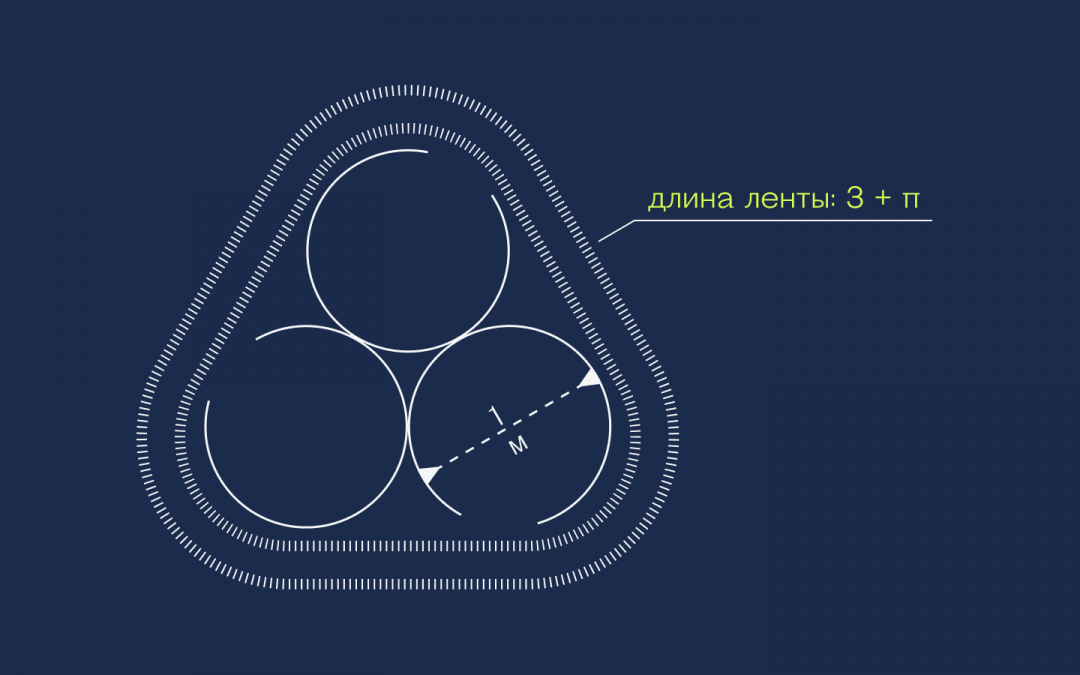
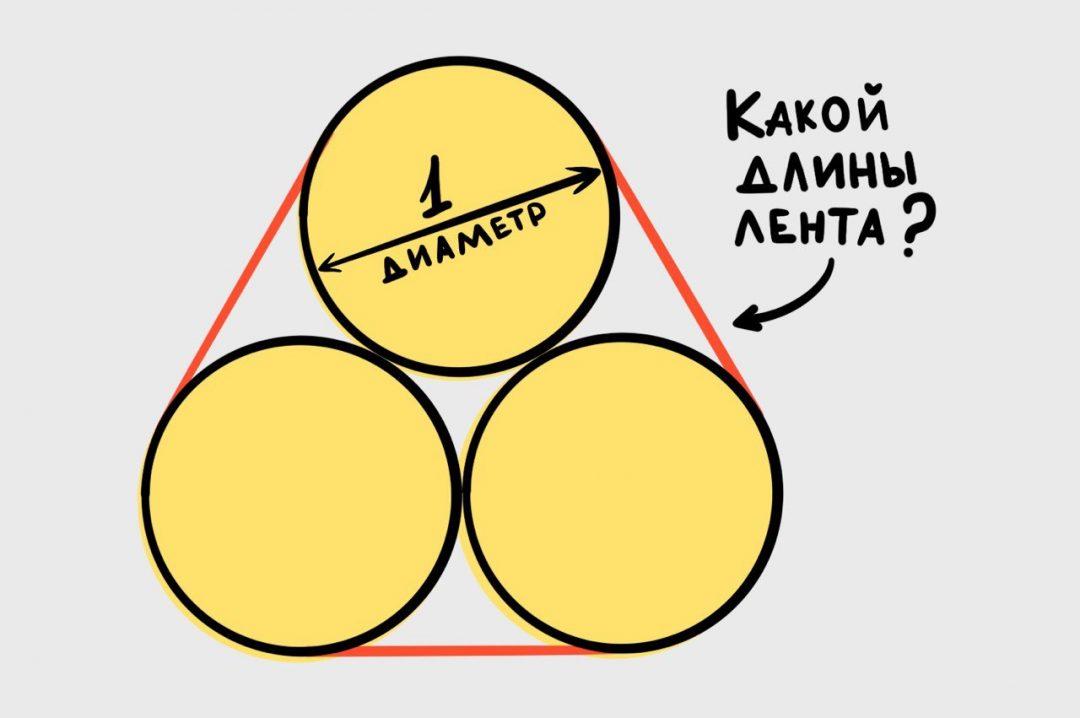
Дано: есть три одинаковых круга с диаметром в 1 метр. Круги соприкасаются друг с другом, а вокруг них натянута эластичная лента.
Что нужно: найти длину этой ленты.
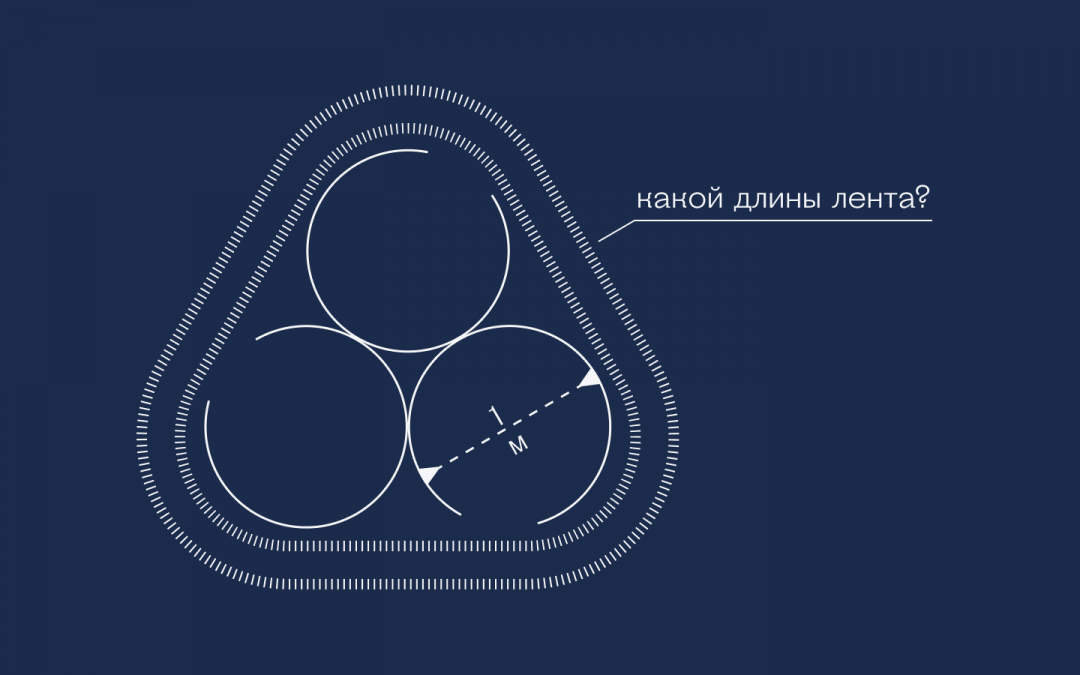
Кажется, что это очень сложная задача, где нужно знать сложные формулы расчёта кривизны и точек натяжения, но на деле всё будет гораздо проще. Если знаете английский — посмотрите оригинальный ролик, там классная анимация:
Строим внутренний треугольник
Первое, что мы сделаем, — соединим центры всех кругов в один треугольник:

В геометрии есть такое правило, что если круги касаются друг друга, то через их центры можно провести прямую линию, и точка касания кругов будет лежать на этой линии. Раз у нас диаметр равен 1, то радиус каждого круга равен 0,5. Обозначим это на рисунке:

Получается, что длина каждой стороны треугольника равна 0,5 + 0,5 = 1. Запомним это и идём дальше.
Строим проекцию
От каждой вершины треугольника проведём под прямым углом линии к ленте:
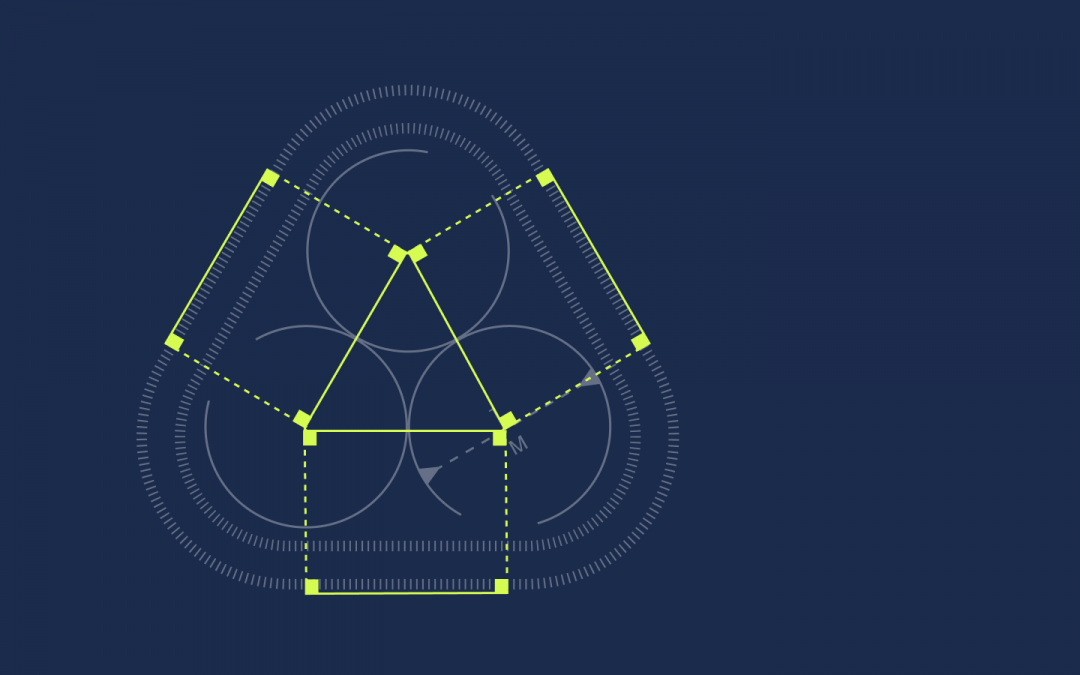
Получились прямоугольники. У прямоугольников противоположные стороны равны, поэтому раз стороны треугольника равны единице, то и эти отрезки на ленте тоже будут равны единице:
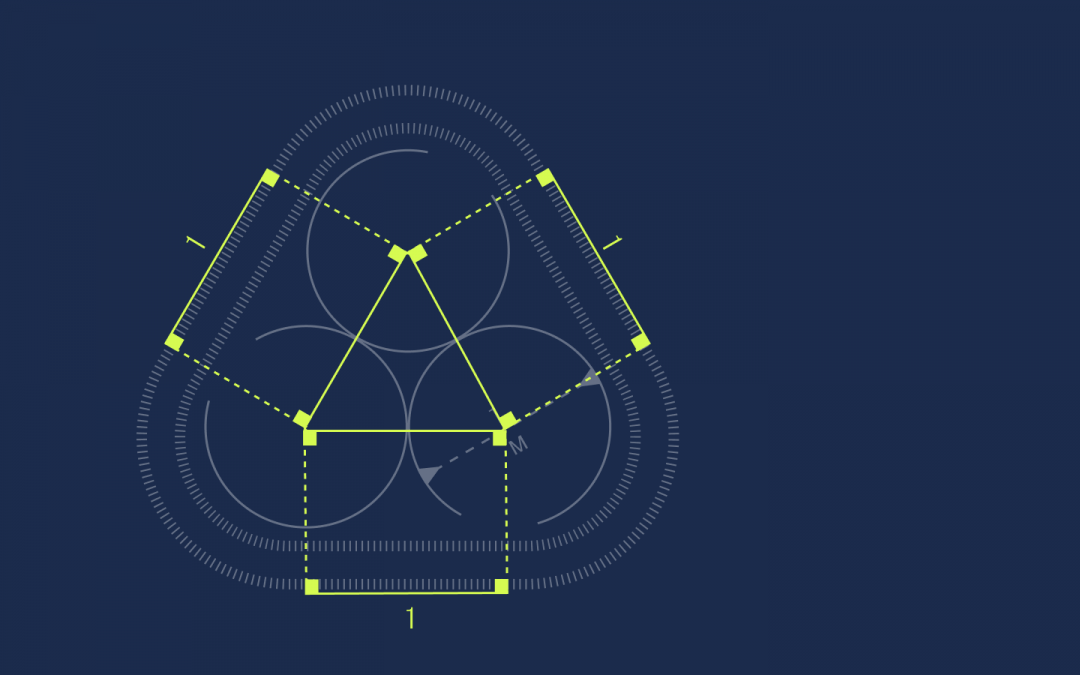
Осталось найти длину оставшихся секций:
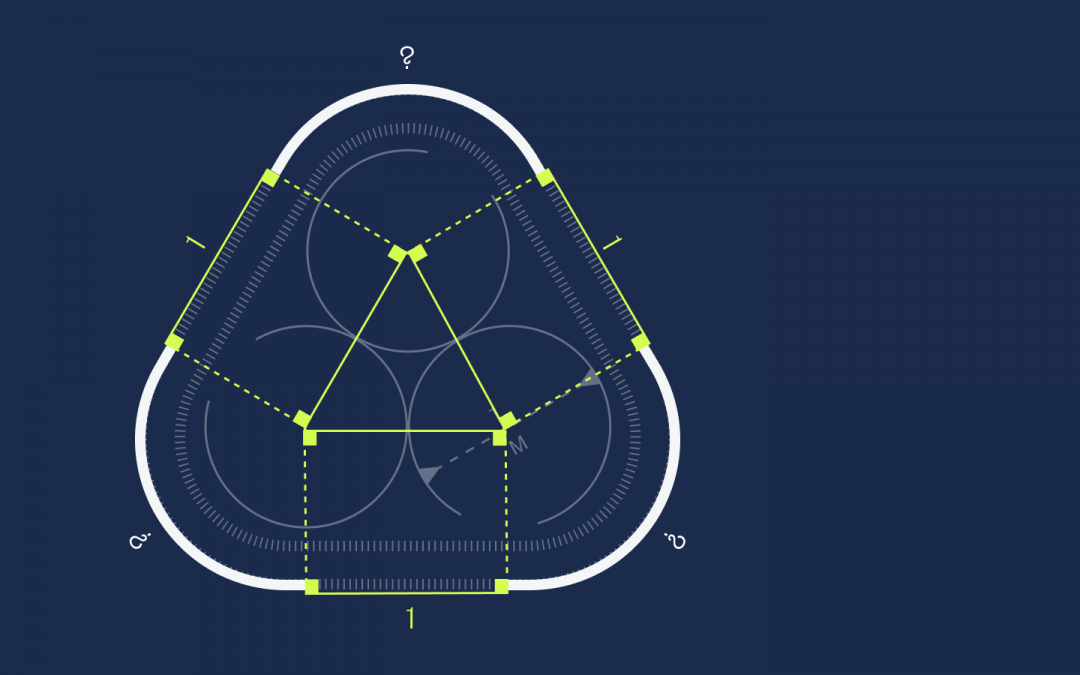
Вычисляем длину секций
Здесь нам поможет знание о том, что полный оборот внутри круга — это 360 градусов.
Так как во внутреннем треугольнике все стороны равны, то это равносторонний треугольник. А раз так, то углы в нём равны 60 градусов. Добавим сюда по два прямых угла по 90 градусов из прямоугольников:
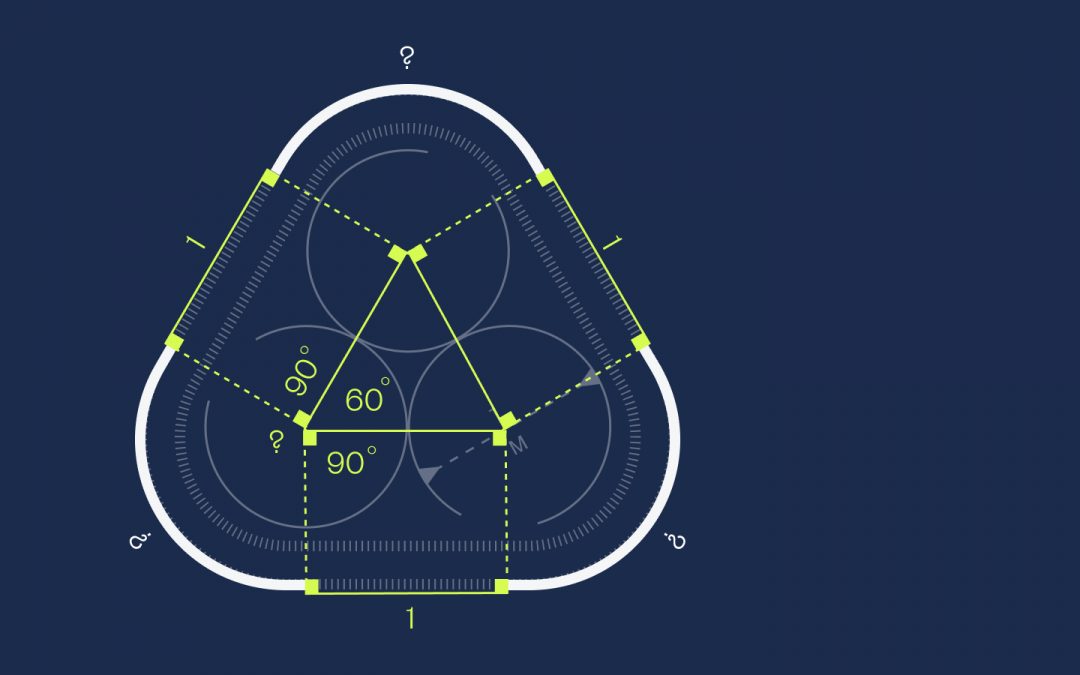
Решаем уравнение: 90 + 60 + 90 + X = 360 → X = 120 градусов.
Но 120 градусов — это ровно треть круга, а у нас таких частей как раз три:
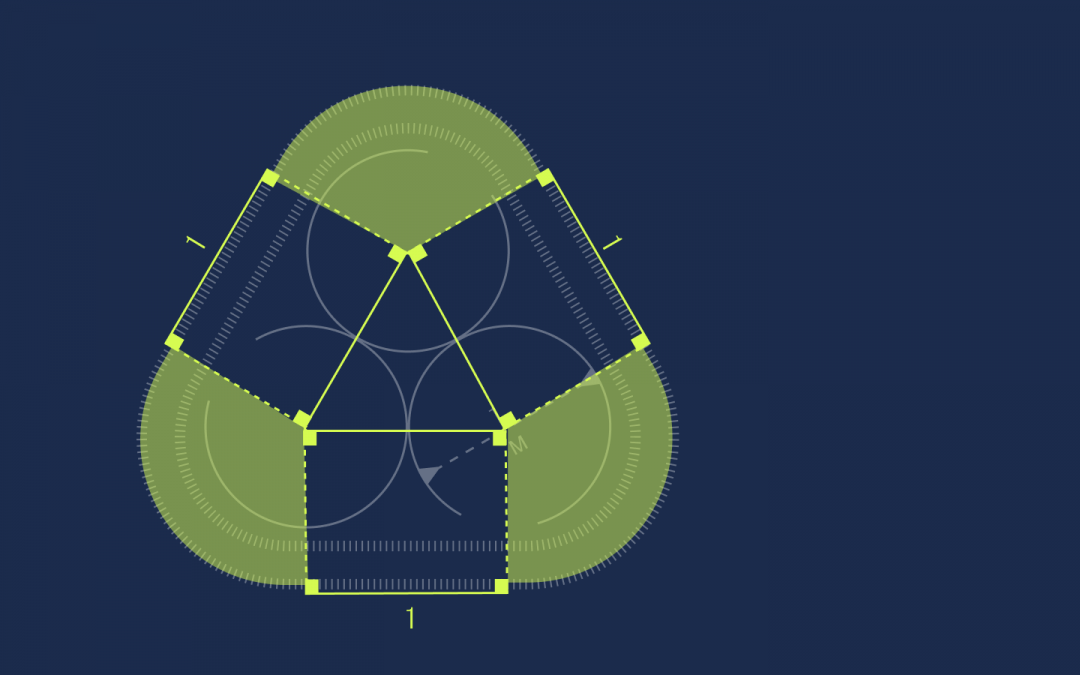
Это значит, что из них можно составить один целый круг. При этом мы знаем, что у этого круга радиус 0,5, а диаметр тогда равен единице. Этого достаточно, чтобы посчитать длину окружности: L = π × d → L = 3,14.
Складываем это число с длинами трёх отрезков и получаем полную длину: 3 + π