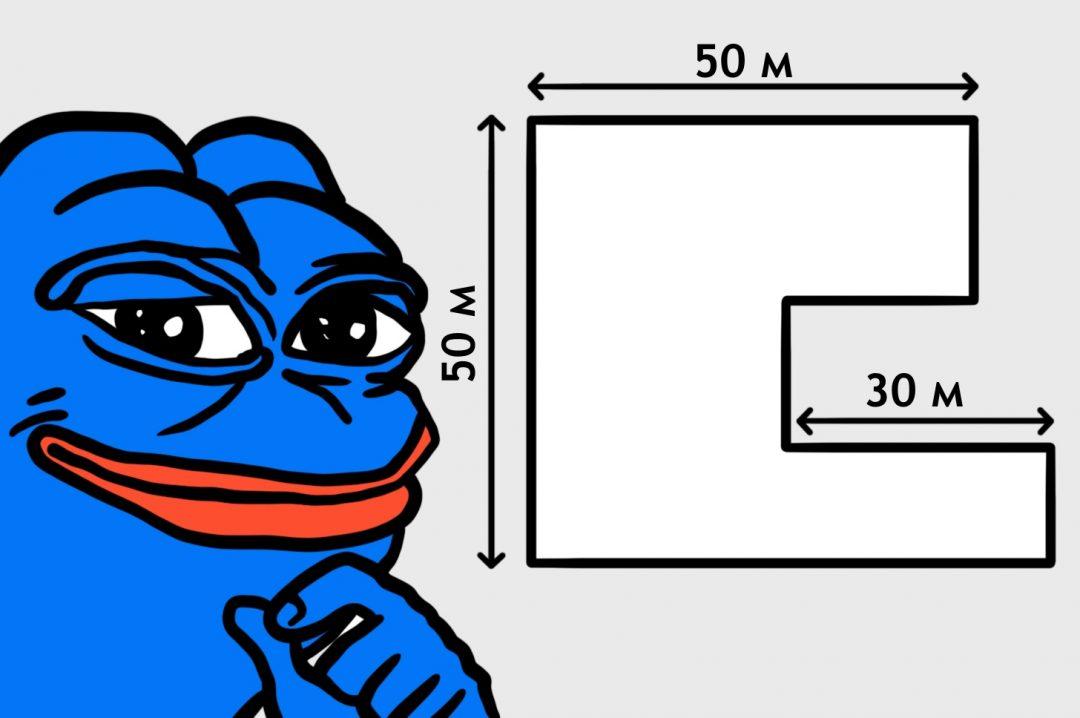
На одном секретном объекте у начальника охраны была задача: установить по периметру высоковольтный забор, чтобы никто не пробрался внутрь. Но объект был настолько секретным, что даже длина забора на всех участках оставалась тайной. Всё, что было у начальника охраны, — это вот такая схема.
Как начальнику охраны вычислить периметр объекта и возможно ли такое в принципе с такими неполными данными? У этой задачи три решения, и если не хотите пробовать сами — читайте наше.
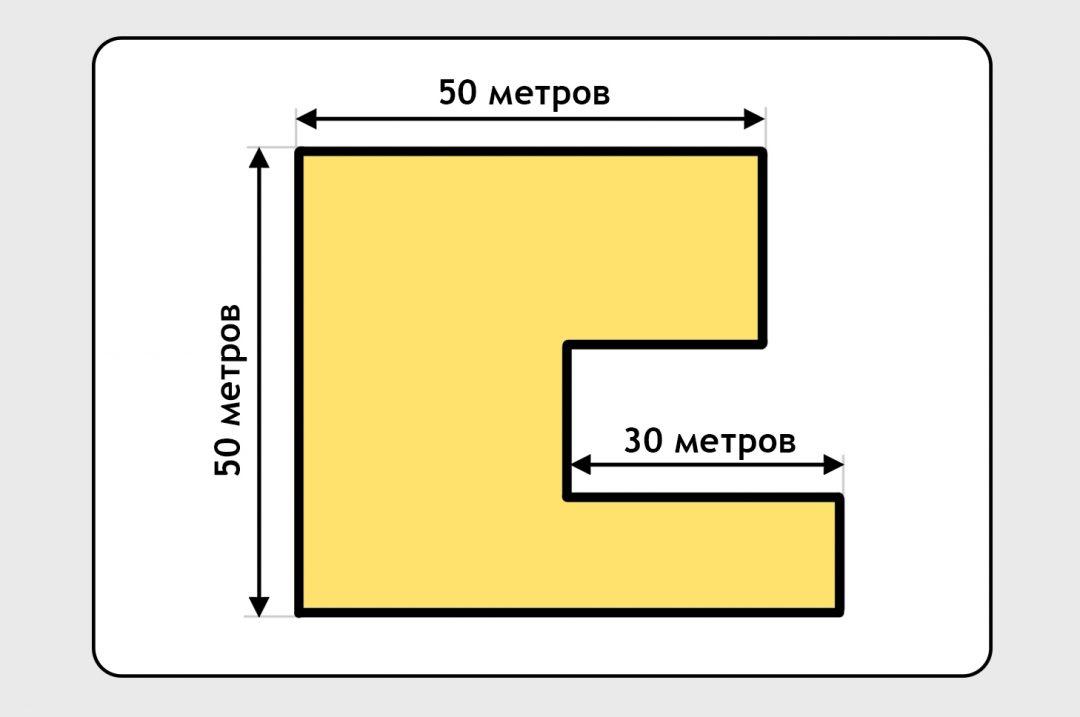
На самом деле все данные для решения у нас уже есть — того, что на рисунке, вполне достаточно.
Сначала находим длину правой стенки — она равна длине левой:
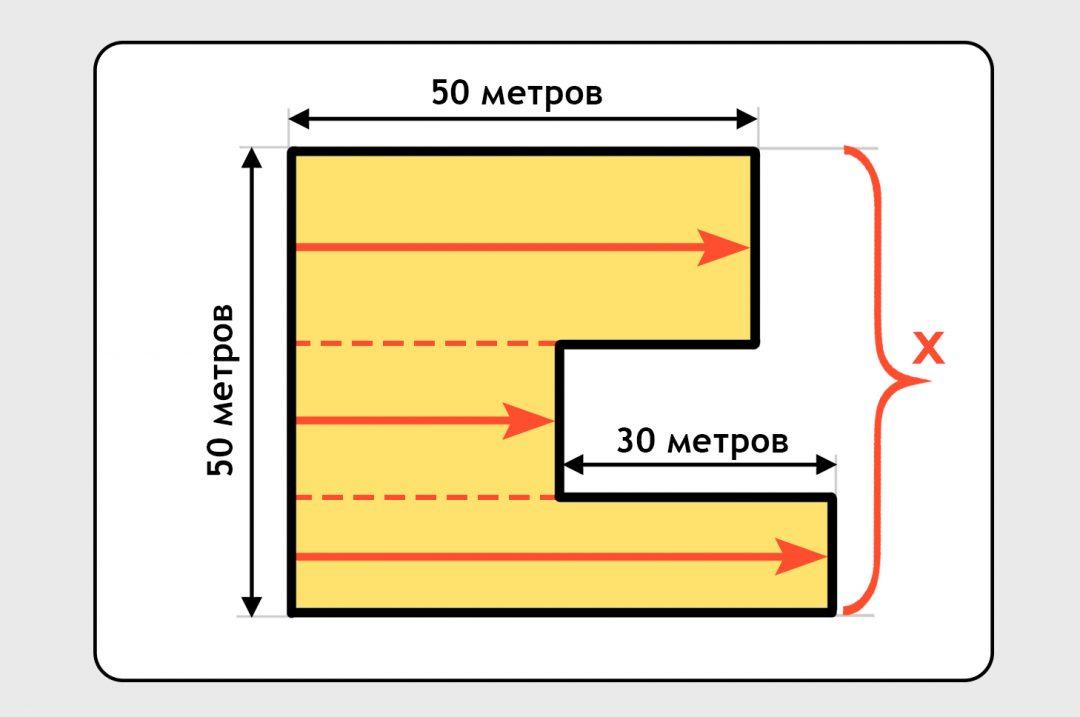
Теперь посчитаем общую длину нижней стенки и двух стен в вырезе. Начнём с нижней: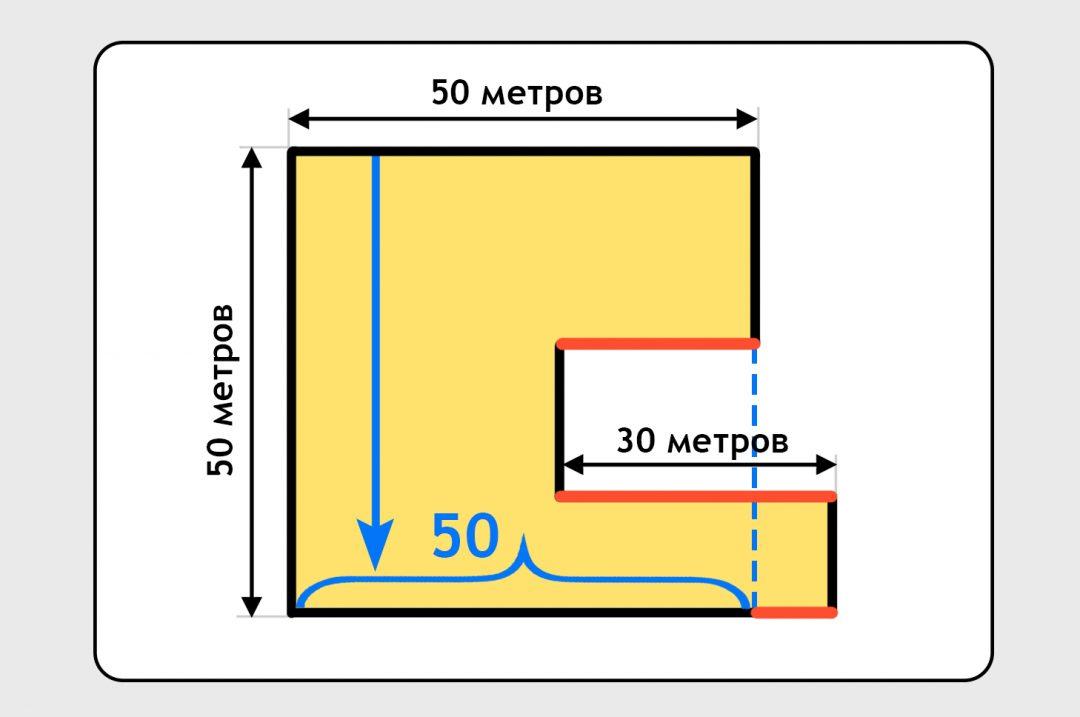 
Видно, что мы уже знаем, чему равен синий участок: тоже 50 метров, как и сверху. Осталось найти, чему равна общая длина красного забора.
Если мы мысленно вырежем нижний короткий красный кусок и перенесём его наверх, то можно легко заметить, что у нас получилось два отрезка по 30 метров:
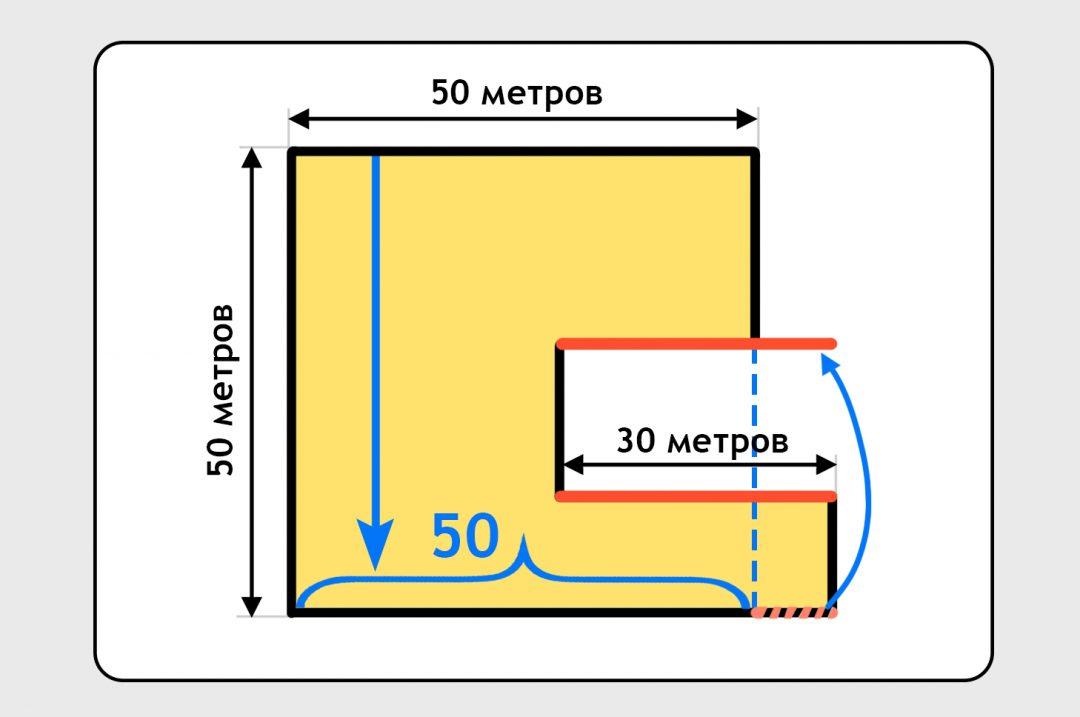
Получается, что длина нижних стен забора будет равна 50 + (30 × 2) = 110 метров.
Тогда общий периметр будет равен: 50 (известно) + 50 (известно) + 50 (правая стенка) + 110 (нижние стенки) = 260 метров. Задача решена!
Чтобы решить задачу инженерным методом, нам понадобится рулетка и допуск начальства для обхода периметра (объект же секретный). Как только получили и то и другое — берём рулетку и измеряем те стены, длина которых нам неизвестна. Как только измерили — складываем результат и получаем нужную длину.
Иногда можно просто взять и измерить :-) Вероятно, изначально выданный нам план неточный, и только прямое измерение даст достоверный результат.
Обозначим все длины, которые нам неизвестны:
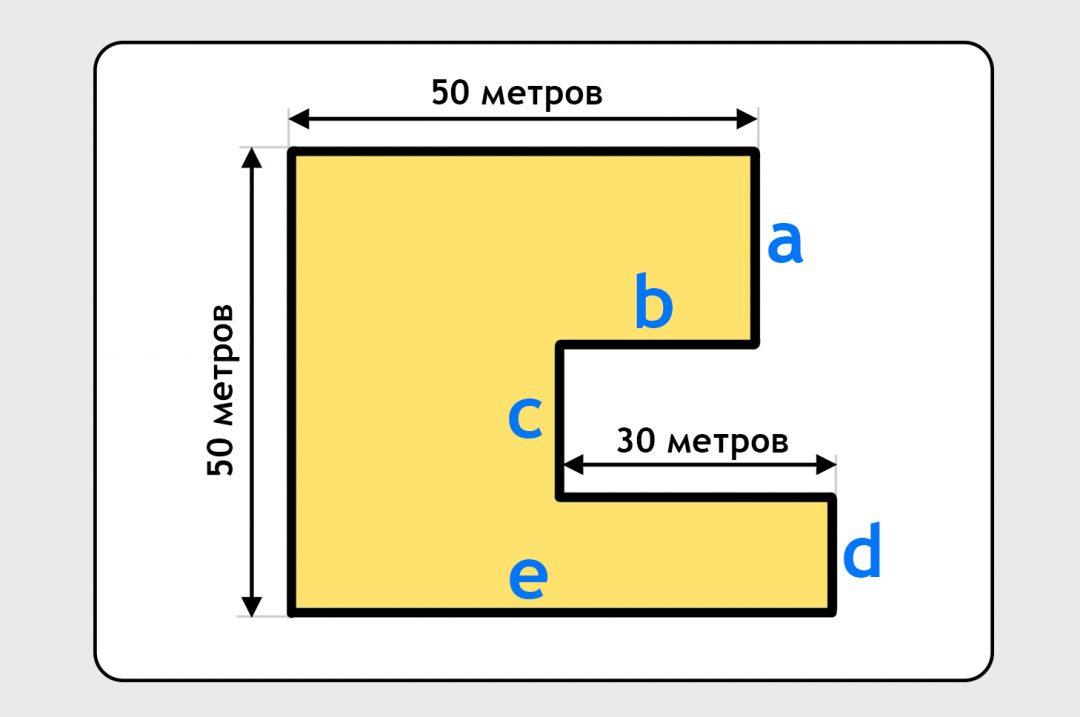
Вот правила, по которым мы будем проверять, соответствует ли наше решение исходным данным:
a + c + d = 50
e – 30 + b = 50
Найдём эти значения и весь периметр методом полного перебора: проверим в циклах все значения, и если они подойдут под наши условия — выводим результат. Если результатов будет несколько — выведем все, пусть дальше с ними разбирается начальник охраны.
Исходя из рисунка, пусть наши переменные не будут больше 50 — этого хватит, чтобы перебрать все доступные значения.
Вот код на JavaScript, простой и рабочий. Вы удивитесь, как много вариантов он найдёт:
var a, b, c, d, e;
// длина каждой стенки не может быть равна нулю, поэтому все циклы начинаются с единицы. Переменная e, судя по рисунку, явно больше 50, поэтому у неё будет другой диапазон
for (a = 1; a <= 50; a++) {
for (b = 1; b <= 50; b++) {
for (c = 1; c <= 50; c++) {
for (d = 1; d <= 50; d++) {
for (e = 1; e <= 100; e++) {
if ((a + c + d == 50) && (e - 30 + b == 50)) {
console.log('a = ' + a);
console.log('b = ' + b);
console.log('c = ' + c);
console.log('d = ' + d);
console.log('e = ' + e);
// 50, 50 и 30 — уже известные нам значения длины
console.log('summ = ' + (50 + 50 + 30 + a + b + c + d + e));
console.log('---------');
}
}
}
}
}
}
