Вот вам безумная мысль:
Есть число 0,99999999… с девятками до бесконечности
Это число равно единице.
То есть 0,9999999… = 1
Как такое возможно? Сейчас разберём.
Может показаться, что всё, что написано ниже, — полная чушь, но на самом деле математика работает именно так. В ней есть странные для понимания вещи, и эта — одна из них.
Обозначим 0,999999… как X:
X = 0,99999…
Умножим обе части на 10. Так как у нас бесконечное число девяток, то 0,99999… превратится в 9,99999… и так тоже до бесконечности:
10X = 9,99999…
Но мы же в самом начале договорились, что X — это 0,99999…, поэтому, раз они равны, вычтем из левой части X, а из правой — это число. Так мы уберём все повторяющиеся девятки после запятой:
10X − X = 9,99999… − 0,99999…
9X = 9
X = 1
А раз у нас было в начале, что X равен 0,99999…, то получается, что:
1 = X = 0,99999…
1 = 0,99999…
Это не очередной математический трюк, мы действительно только что доказали, что 0,99999… = 1.
Вспомним обычные дроби и разделим единицу на 3 — получим ⅓.
Если мы попробуем разделить 1 на 3, то получим бесконечные тройки:
⅓ = 0,33333…
При этом если мы умножим простую дробь ⅓ на 3, то получим обратно целую единицу:
(1 / 3) × 3 = (1 × 3) / 3 = 3 / 3 = 1
Но мы знаем, что ⅓ — это 0,33333…, поэтому если мы умножим обе части на три, то тоже получим целую единицу:
⅓ × 3 = 0,33333… × 3
1 = 0,99999…
Мы снова только что доказали это.
Используем классическое определение рядов и пределов из курса математического анализа. Если упростить, то предел — это к какому числу стремится какая-то бесконечная конструкция.
Раз у нас в числе 0,99999… количество девяток стремится к бесконечности, то это можно записать как обычный предел:
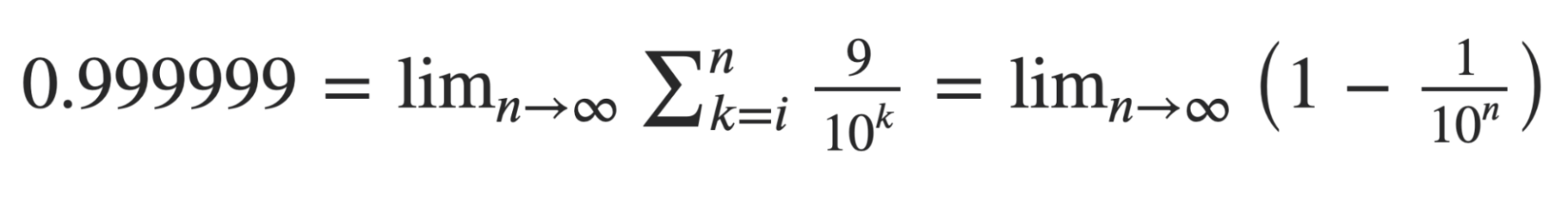
Решая этот предел, мы придём к такому:
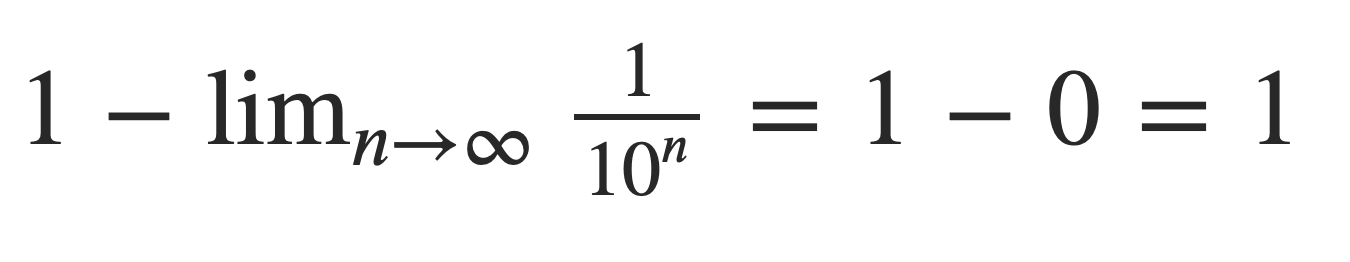
Получается, мы через пределы доказали, что 0,99999… = 1.
Допустим, что мы хотим посчитать разницу между единицей и 0,99999…:
1 − 0,99999… = ?
Если наш ответ будет что-то вроде «ну, тут бесконечное число нулей, а потом единица», то получается, что наше бесконечное число нулей в какой-то момент заканчивается. Но это странно, потому что девяток-то у нас точно бесконечно много и они не заканчиваются. А нули — заканчиваются и потом единица.
Но так не бывает, что бесконечность внезапно заканчивается, а значит, наше предположение, что в конце будет единица — неверно. Получается, что нули в ответе никогда не закончатся, а значит, и весь ответ будет равен нулю:
1 − 0,99999… = 0
А раз так, то левая часть равна правой. Мы доказали это. Снова.
Спокойно, выдыхайте. Всё дело в «бесконечном числе девяток», а конкретно — в понятии «бесконечности». Бесконечность — виртуальное понятие, у которого нет представления в реальности. Бесконечность ломает наши представления о реальности.
Представьте так: у вас есть голова сыра весом ровно 1 кг. Вам нужно снять с неё стружку так, чтобы сыр стал весить 0,999… кг. Какого веса должна быть эта стружка? Если новый вес должен быть 0,999… до бесконечности, то стружка должна быть 0,000… до бесконечности. То есть 0.
Расчехляйте арифмометры и заходите в «Практикум» на продвинутую математику.
