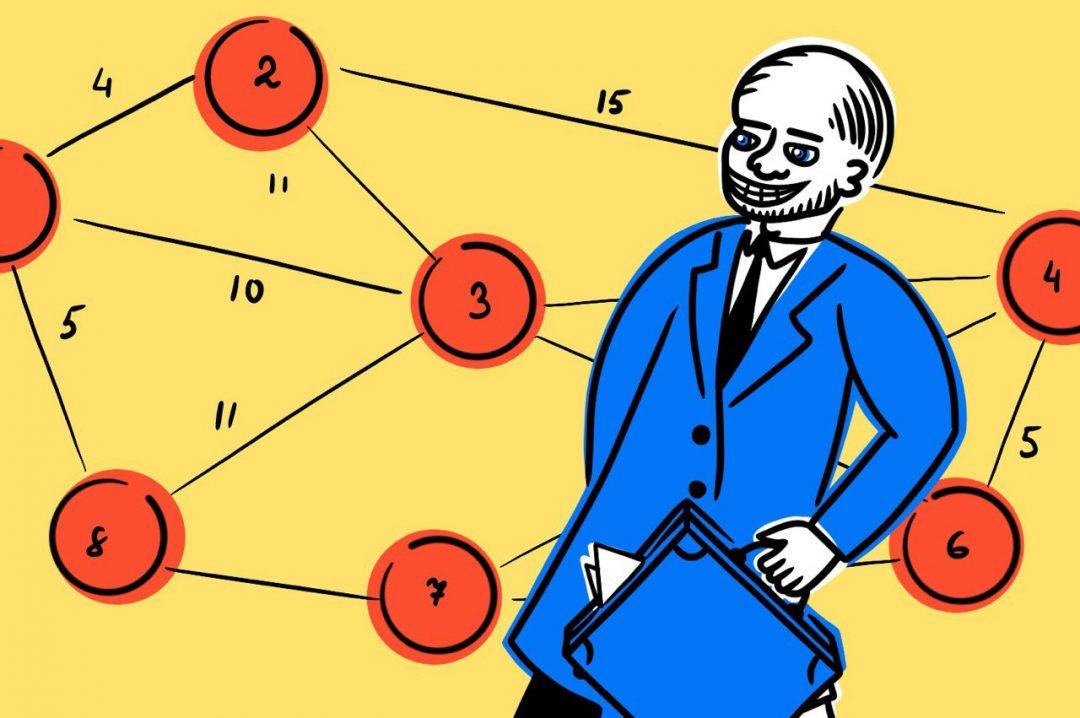
Что такое «задача коммивояжёра»

В 19-м и 20-м веке по городам ездили коммивояжёры (сейчас их называют «торговые представители»). Они ходили по домам и предлагали людям купить разные товары. Тактика была такой: коммивояжёр приезжал в город, обходил большинство домов и отправлялся в следующий город. Города были небольшими, поэтому обойти всё было вполне реально.

Чем больше городов посетит коммивояжёр, тем больше домов он сможет обойти и больше заработать с продаж. Самая большая проблема, которая всегда стояла перед коммивояжёрами, звучала так:

как быстрее всего объехать все города в этом районе?

В 19-м веке все добирались из города в город на лошадях и повозках, поэтому время полностью зависело от расстояния между городами. С другой стороны, коммивояжёру нужно было вернуться домой после поездок, поэтому классическая задача коммивояжёра звучит так:

как найти самый короткий маршрут между городами, чтобы побыть в каждом хотя бы по одному разу и вернуться домой.

Кажется, что задача очень простая и современные компьютеры могут быстро её решить, но это не так. Если городов будет больше 66, то компьютеру понадобится несколько миллиардов лет, чтобы найти правильный ответ. Давайте выясним, почему это так.

Как устроен и зачем нужен квантовый компьютер

Что такого особенного в этой задаче?

На самом деле это задача не про расстояния, а про поиск оптимального решения по выбранному параметру в сложной системе. Дело в том, что расстояние — это только одна характеристика маршрута. А могут быть и другие:

Время в пути. Время не обязательно напрямую зависит от расстояния. Например, в Санкт-Петербурге можно пойти ночью самым коротким путём и застрять на разводке мостов. По расстоянию это будет километр, а по времени — три часа.

Количество и частота. У нас могут быть лимиты на посещения: не более или не менее определённого количества городов. В классической задаче — нужно побыть в каждом городе не менее одного раза. Также могут быть ограничения вроде «не более одного раза» или «побывать в каждом городе дважды».

Направление движения. Не по всем дорогам можно проехать в обе стороны — есть направления с односторонним движением. Это значит, например, что из одной точки до другой не получится доехать напрямую. Значит, придётся выбирать другой маршрут.

Зависимости. Например, вам нужно по пути отвезти документы в одно учреждение, но перед этим забрать их в другом. Если не выполнить этот порядок, поездка теряет смысл, потому что не выполнено важное условие.

Всё сразу. Может оказаться так, что нам нужно построить такой маршрут:

посетить все города центрального региона России самым коротким путём;
в каждом городе посмотреть три главных достопримечательности;
потратив минимум денег на дорогу и проживание;
побывать в каждом городе не больше одного раза;
и успеть всё это за 5 дней.

Всё и сразу не получится

Возьмём для примера маршрут по городам России. В нём 5 условий:

Все города региона.
Каждый город проезжать не более одного раза.
Общая длина маршрута должна быть минимальной.
Общая сумма потраченных денег на дорогу и проживание должна быть минимальной.
Общая длительность поездки не должна превышать 5 дней.

Скорее всего, ни нам, ни компьютеру не получится построить такой маршрут, чтобы выполнить все условия сразу. Это окажется физически невозможно.

Чтобы такого не было, заранее выбирают одно или два критичных условия, а остальное как получится. Например, нам важно уложиться в 5 дней. Вторым важным параметром, допустим, выберем просто посещение каждого города. Вот что у нас получится в итоге:

⚠️ Все города региона.
⚠️ Общая длительность поездки не должна превышать 5 дней.
Каждый город можно проезжать сколько угодно раз.
Общая длина маршрута — как получится.
Хотелось бы, чтобы общая сумма потраченных денег на дорогу и проживание должна быть минимальной, но на всякий случай возьмём с собой денег с запасом.

Теперь нам гораздо проще построить такой маршрут, потому что есть главные критерии, а остальным можно пожертвовать.

Почему это сложно для компьютера

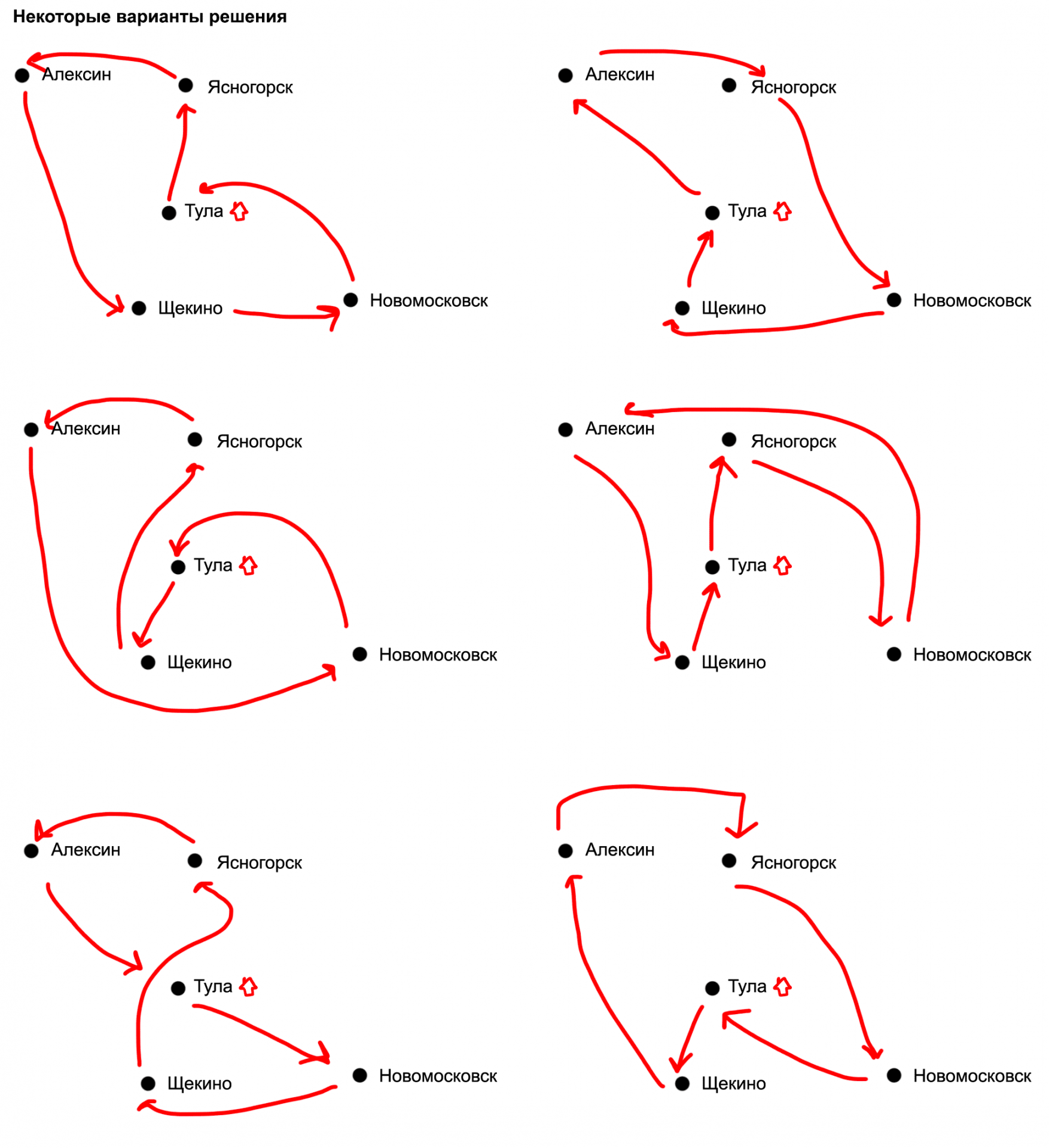
Возьмём простой случай: у нас есть города и таблица расстояний между ними. Задача — найти самый короткий маршрут посещения всех городов ровно по одному разу, без возвращения в первый город.

Если у нас в таблице 4 города, то вариантов первого выбора у нас тоже 4.
Когда мы выбрали первый город, то у нас есть 3 варианта, в какой город поехать вторым.
Во втором городе у нас вариантов следующего города осталось 2 — третий либо четвёртый.
В третьем городе у нас остаётся всего один вариант, куда поехать для завершения маршрута.

Так как в города мы можем поехать в любой последовательности, то всего у нас получается 4 × 3 × 2 × 1 = 24 варианта маршрута. Это называется факториал числа, когда нам нужно последовательно перемножить все числа от 1 до этого числа.

Когда у нас 24 варианта и всего один параметр — минимальный маршрут, — компьютер легко с этим справится простым перебором. Но если таких городов будет уже 15, у нас появится почти полтора миллиарда комбинаций маршрутов. Это уже сложнее, но за час-полтора мощный компьютер справится и с этим. И это только с одним параметром!

Если мы к 15 добавим ещё два города, то получим уже 355 миллиардов комбинаций. Такой объём вычислений потребует гораздо больше времени.Теоретический предел для компьютера — 66 городов. Если городов 67, то число возможных комбинаций маршрутов будет равно 36×10⁹³ — это больше предела Бремерманна. Для справки, в России 173 города.

👉 Что за предел Бремерманна

Представьте компьютер размером с нашу Землю на современных транзисторных процессорах. В нём миллиарды миллиардов транзисторов, и все они работают на максимально возможной частоте. Такой компьютер может обработать 10⁷⁵ операций в секунду. Если такой компьютер будет работать столько, сколько существует Земля, то за всё это время он сможет обработать 10⁹³ бит информации. А при 67 городах наше число маршрутов получается в 36 раз больше, поэтому компьютер никогда не сможет рассчитать нужный нам маршрут.

И что тогда делать?

Если нам нужен самый короткий идеальный маршрут, то мы сможем его найти только для небольшого числа городов. Но если можно отойти от идеала и сделать маршрут чуть длиннее, то с этим компьютер уже может справиться.

Дело в том, что когда мы добавляем допустимую погрешность в решение, компьютеру становится намного проще найти ответ. В этом случае задача сводится к тому, чтобы подобрать любой маршрут, который укладывается в рамки допустимой погрешности. Для этого используют специальные алгоритмы, которые позволяют за приемлемое время найти маршрут с погрешностью 1% от минимальной длины.

Где применяется

На алгоритмах решения задачи коммивояжёра построены все современные навигаторы в машинах и телефонах. Ведь ровно это алгоритм и делает: ищет самый короткий маршрут между двумя точками, а в качестве промежуточных «городов» у него перекрёстки.

Но это не единственное применение этого алгоритма, ещё он используется:

для организации логистики и перевозок в крупных компаниях, чтобы строить оптимальные маршруты по времени, объёму груза и топливу;
в системах принятия решений, когда на входе есть много параметров и нужно найти оптимальную цепочку действий;
на производстве при организации конвейера, чтобы сократить время простоя и сделать сборку деталей максимально эффективной;
при составлении туристических маршрутов;
в экономике для анализа эффективности финансовых инструментов.