Вчера мы рассказывали, что такое задача коммивояжёра. Если коротко — это класс задач на поиск кратчайшего маршрута среди нескольких городов. Или маршрута по городу. Или поиск оптимальной квартиры для аренды по нескольким параметрам. В общем — это задачи о том, как принимать решения в ситуациях со множеством переменных.
Сегодня мы попробуем решить классическую задачу коммивояжёра самым простым способом — простым полным перебором.
👉 Мы знаем, что решить задачу коммивояжёра полным перебором не получится, если у нас много городов. Но мы попробуем и посмотрим, какой получится код и как его можно оптимизировать.
Города и расстояния
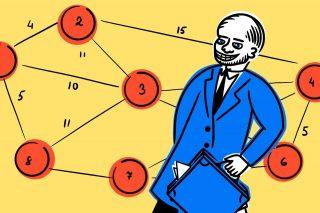
Допустим, у нас есть 5 городов, каждый из которых соединён с другим:

Из-за рельефа местности близкие города не всегда соединены по прямой, но для простоты мы нарисовали так. Теперь проставим время, которое требуется для переезда из города в город:

Чтобы было удобно пользоваться расстояниями, сделаем табличку:
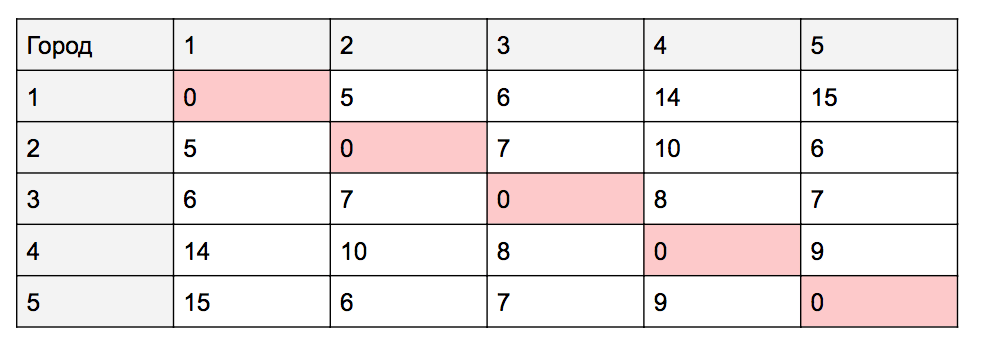
Нулевые ячейки означают, что здесь нет маршрута, потому что это путь из одного и того же города и обратно. Остальные числа — это расстояния между городами. Например, расстояние между первым и третьим городом — 6 километров, а между четвёртым и вторым — 10 километров.
На языке JavaScript это будет выглядеть так:
// таблица с расстояниями между городами
var towns = [
[0, 5, 6, 14, 15],
[5, 0, 7, 10, 6],
[6, 7, 0, 8, 7],
[14, 10, 8, 0, 9],
[15, 6, 7, 9, 0]
];Логика работы
Наша задача — найти такой маршрут, в котором сумма километров будет минимальной.
Скрипт полного перебора будет работать так:
- С помощью 5 вложенных циклов мы сможем перебрать все варианты маршрутов.
- В каждом цикле проходим от 0 до 4, потому что у нас 5 городов. Если бы у нас было 10 городов, нам нужно было бы сделать 10 вложенных циклов и в каждом цикле проходить от 0 до 9, чтобы перебрать все возможные расстояния для этого города.
- На каждом шаге проверяем, чтобы у нас не повторялись города в маршруте, потому что в каждом можно побывать только один раз.
- Если это условие выполняется, то запоминаем очередной маршрут и считаем его длину.
- Если длина получилась меньше, чем наименьшая до этого — значит, сейчас у нас получился самый короткий маршрут. Возможно, на следующих шагах цикла мы найдём маршрут ещё короче, но пока минимальный — этот. Делаем эту длину наименьшей и запоминаем номер маршрута.
- Так прогоняем все комбинации городов.
- Выводим найденный минимальный маршрут и его длину.
Скрипт
Для работы скрипта нам понадобятся такие переменные:
- Массив, где мы будем хранить все просчитанные маршруты.
- Порядковый номер текущего маршрута. Как только обрабатываем очередной маршрут, будем увеличивать номер на единицу, чтобы сохранить новый маршрут под новым номером.
- Переменная, где хранится самый короткий путь. Чтобы уже на первом шаге у нас было с чем сравнивать длину маршрута, поместим в неё заведомо большое число, например, 10 000 километров. Как только мы найдём путь короче (а мы найдём), заменим его новым минимальным расстоянием.
- Номер самого короткого маршрута. С его помощью мы вытащим из массива со всеми маршрутами самый короткий из них.
Соберём скрипт. Читайте комментарии:
// таблица с расстояниями между городами
var towns = [
[0, 5, 6, 14, 15],
[5, 0, 7, 10, 6],
[6, 7, 0, 8, 7],
[14, 10, 8, 0, 9],
[15, 6, 7, 9, 0]
];
// массив, где будут храниться все просчитанные маршруты
var path =[];
// порядковый номер текущего маршрута
var counter = 0;
// самый короткий путь — сразу ставим заведомо большим, чтобы уменьшать его по мере работы алгоритма
var minPath = 10000;
// номер самого короткого маршрута
var minCounter;
// перебираем все варианты перемещения по городам
for (var i1 = 0; i1 <=4; i1++) {
for (var i2 = 0; i2 <=4; i2++) {
for (var i3 = 0; i3 <=4; i3++) {
for (var i4 = 0; i4 <=4; i4++) {
for (var i5 = 0; i5 <=4; i5++) {
// нельзя посещать один и тот же город больше одного раза
if (
(i1 != i2) && (i1 != i3) && (i1 != i4) && (i1 != i5) &&
(i2 != i3) && (i2 != i4) && (i2 != i5) &&
(i3 != i4) && (i3 != i5) &&
(i4 != i5)
)
{
// запоминаем текущий путь
path[counter] = (i1+1) + ' → ' + (i2 + 1) +' → ' + (i3 + 1) + ' → ' + (i4 + 1) + ' → ' + (i5 + 1);
// выводим его в консоль
console.log(path[counter]);
// если общее расстоения этого пути меньше минимального
if ( (towns[i1][i2] + towns[i2][i3] + towns[i3][i4] + towns[i4][i5]) < minPath) {
// то мы запоминаем это минимальное расстояние
minPath = towns[i1][i2] + towns[i2][i3] + towns[i3][i4] + towns[i4][i5];
// выводим его в консоль
console.log(minPath);
// запоминаем номер этого маршрута с минимальным расстоянием
minCounter = counter;
}
// когда всё сделали, увеличиваем номер маршрута
counter +=1;
}
}
}
}
}
};
// когда прошли все варианты, выводим найденное решение
console.log('Путь с самой короткой длиной маршрута: ' + path[minCounter] + '(' + minPath + ' км.)');Разбираем результат
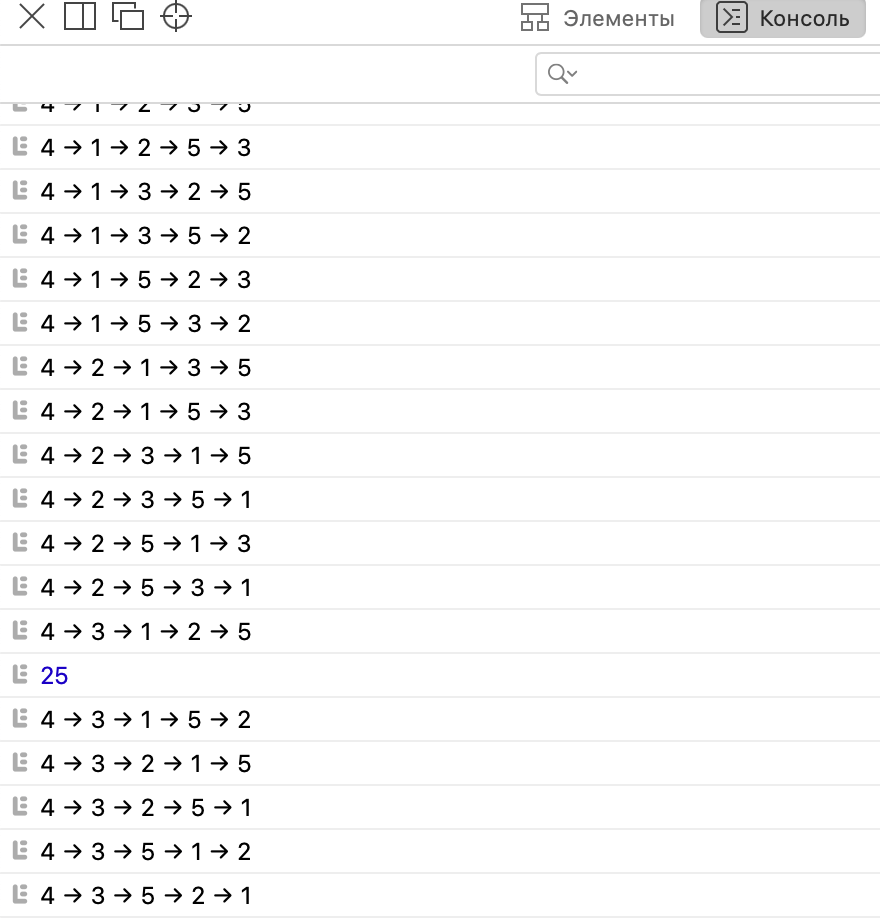
Когда мы запустим скрипт в консоли браузера, то увидим такое:

Скрипт на каждом шаге выводил текущий маршрут, который он проверял, а в конце выдал результат. Если мы пролистаем наверх весь вывод маршрутов, то увидим, как скрипт постепенно находил маршруты всё короче и короче:

Но только ближе к концу он нашёл самый короткий путь, который и вошёл в итоговый результат:
Что здесь не так
С одной стороны, у нас получился простой и понятный алгоритм, который делает то, что нам нужно. С другой — у него есть серьёзные проблемы:
- Если у нас будет 15 городов, нам нужно будет делать 15 вложенных циклов и делать 120 проверок — это выглядит очень громоздко, легко ошибиться в таком коде.
- Чем больше будет городов, тем медленнее будет считаться результат. Уже на 10 городах мы получим 3,5 миллиона выполнений тела цикла, что займёт гораздо больше времени. На 13 городах таких выполнений будет уже 6 миллиардов, и компьютер может их считать неделю или даже больше.
Попробуем исправить эти недостатки в следующих подходах к задаче. Следите за новыми статьями.