Чтобы отличить оптимизм от пессимизма, достаточно налить в стакан жидкость на половину его объёма. Определить половину несложно — она будет посередине высоты стакана. А как быть, если у нас не стакан, а бокал на ножке?
Если брать за высоту бокала расстояние от краёв до пятки (места, где ножка соединяется с чашей), варианты такие:
- 50%,
- 60%,
- 70%,
- 80%,
- 90%.
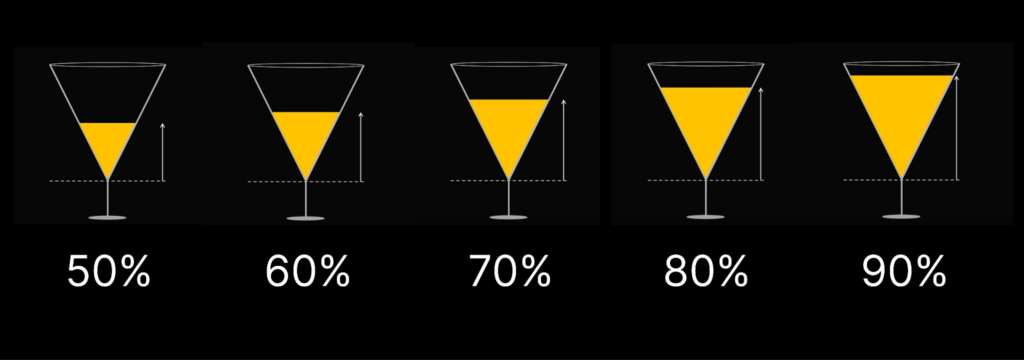
В каком случае можно утверждать, что бокал наполовину полон (или пуст)? А может, всё зависит от внутреннего угла чаши?
Геометрически чаша бокала больше всего похожа на прямоугольный конус, или прямой круговой конус:
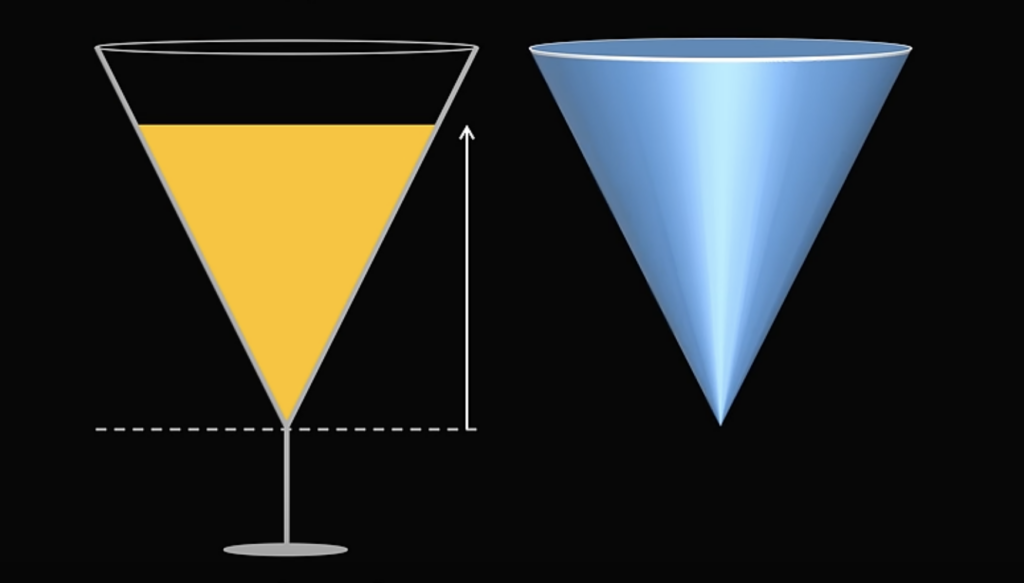
Такой конус можно получить, если вращать прямоугольный треугольник вокруг прямой, которая содержит один из его катетов. Прямая будет высотой H, а катет-основание — радиусом R:
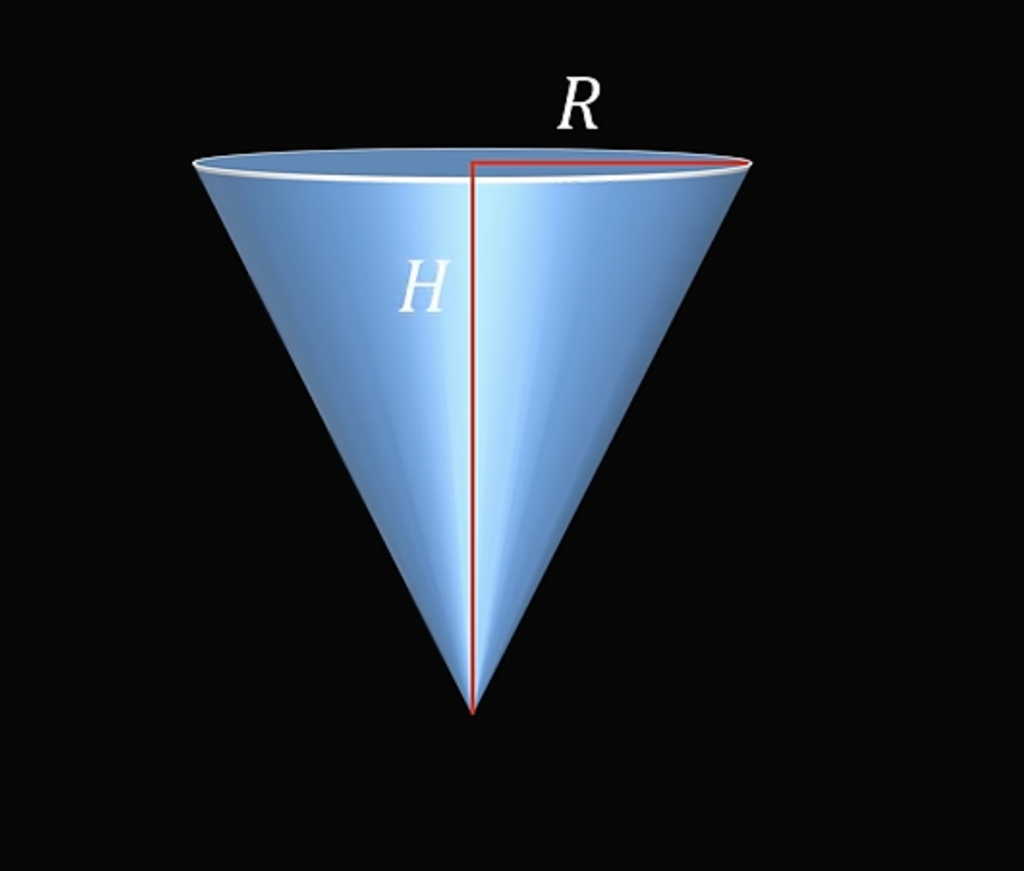
Объём такого конуса можно вычислить по формуле:
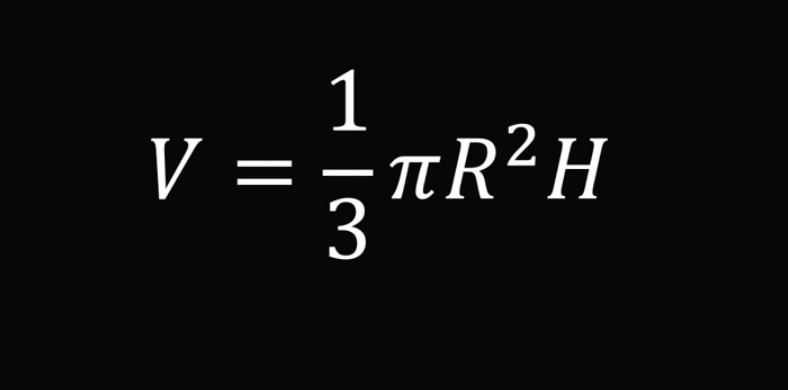
Теперь представим, что внутри нашего конуса есть ещё один конус поменьше с высотой h и радиусом r:
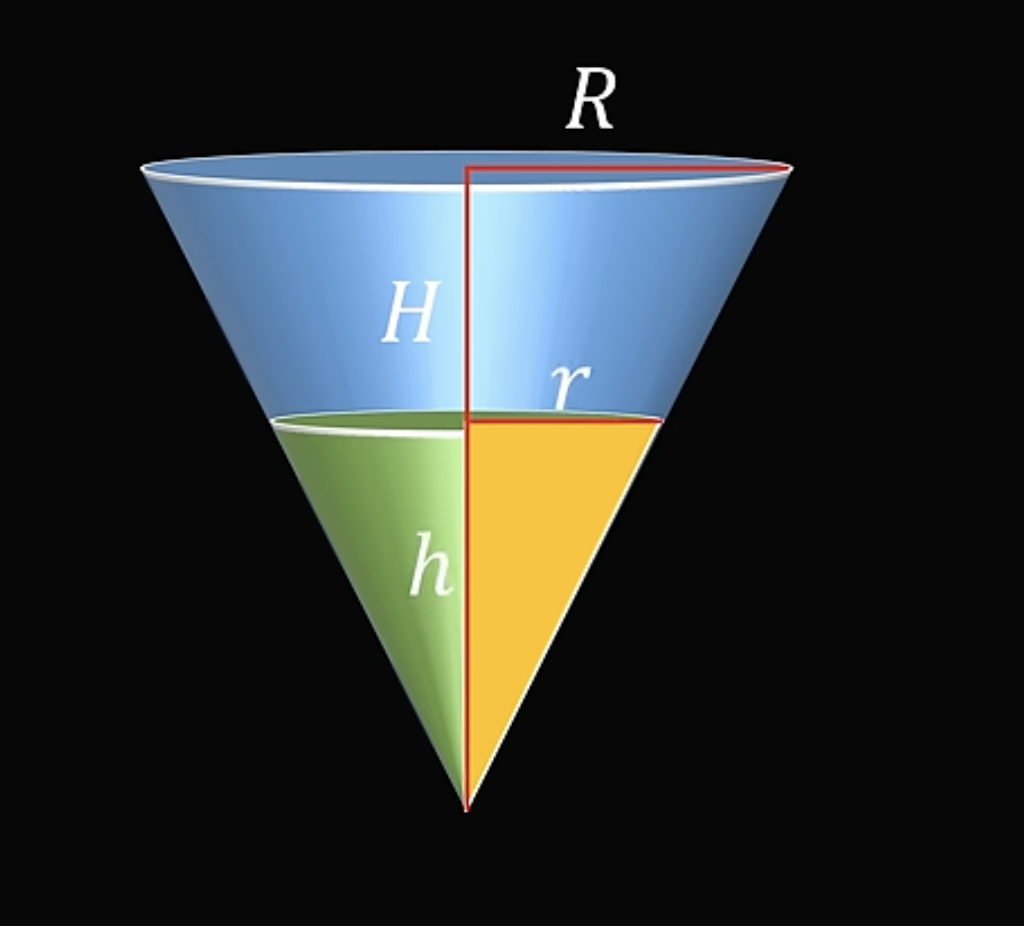
Объём этого конуса поменьше можно вычислить по формуле:
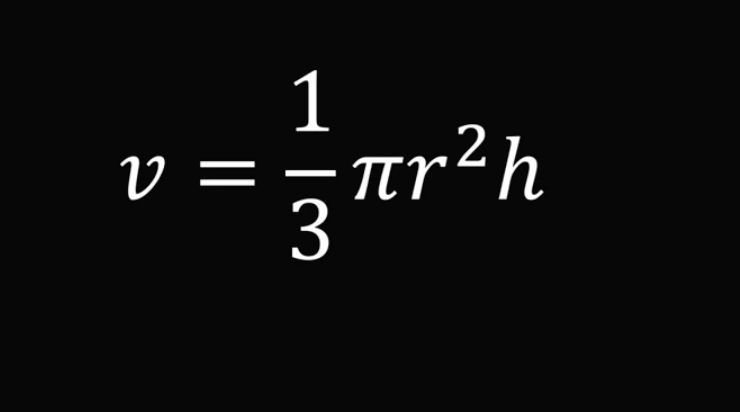
Соотнесём объёмы этих двух конусов. В конусе поменьше есть прямоугольный треугольник, где одна из сторон — радиус r, а другая — высота h. В большом конусе у нас другой прямоугольный треугольник, стороны которого — радиус R и высота H.
Получается, что маленький и большой конусы имеют разные размеры, но одинаковую форму. Значит, два треугольника подобны, и отношения соответствующих сторон равны:
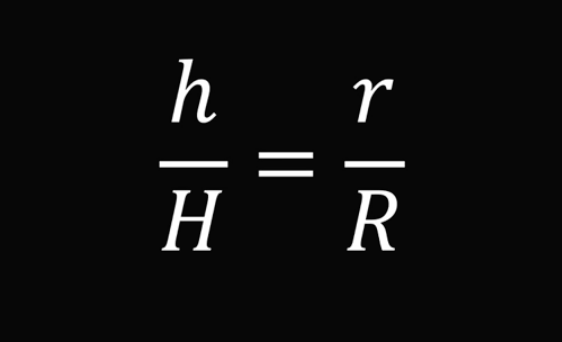
А соотношение объёмов маленького и большого конусов можно представить в виде такого равенства:
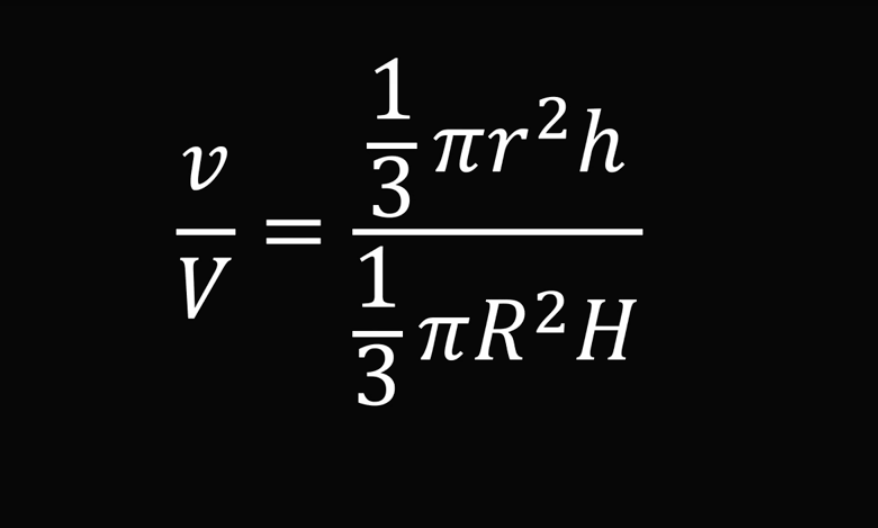
Числитель и знаменатель дроби в правой части этого равенства содержат общие множители 1/3 и π, так что эту дробь можно сократить — убрать одинаковые элементы. Тогда получим:
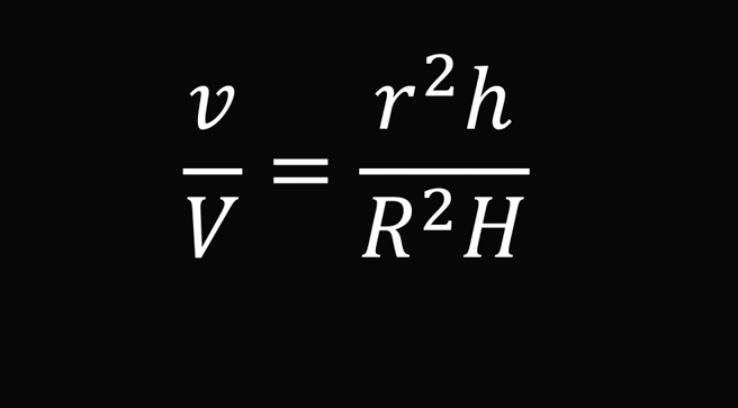
Упростим равенство ещё больше и получим:
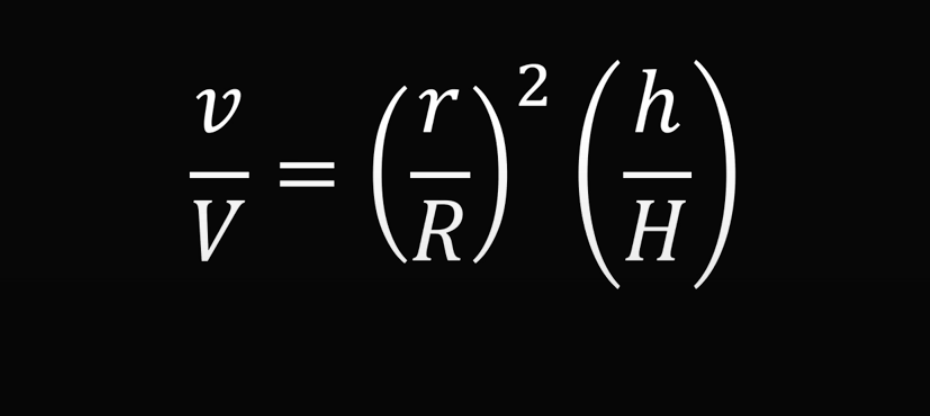
Выше мы уже определили, что отношения соответствующих сторон двух треугольников равны. Это значит, что наше равенство можно записать так:
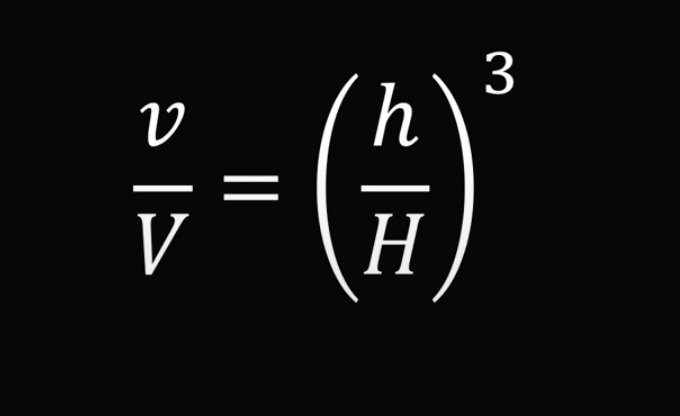
Тогда получается, что соотношение v/V — процент объёма, а соотношение h/H — процент высоты. Из этого следует равенство:
% объёма = (% высоты)3
Как мы видим, равенство никак не зависит от радиуса конуса или внутреннего угла его вершины. Если представить это равенство на графике со значениями % высоты на оси X и % объёма на оси Y, получится парабола:
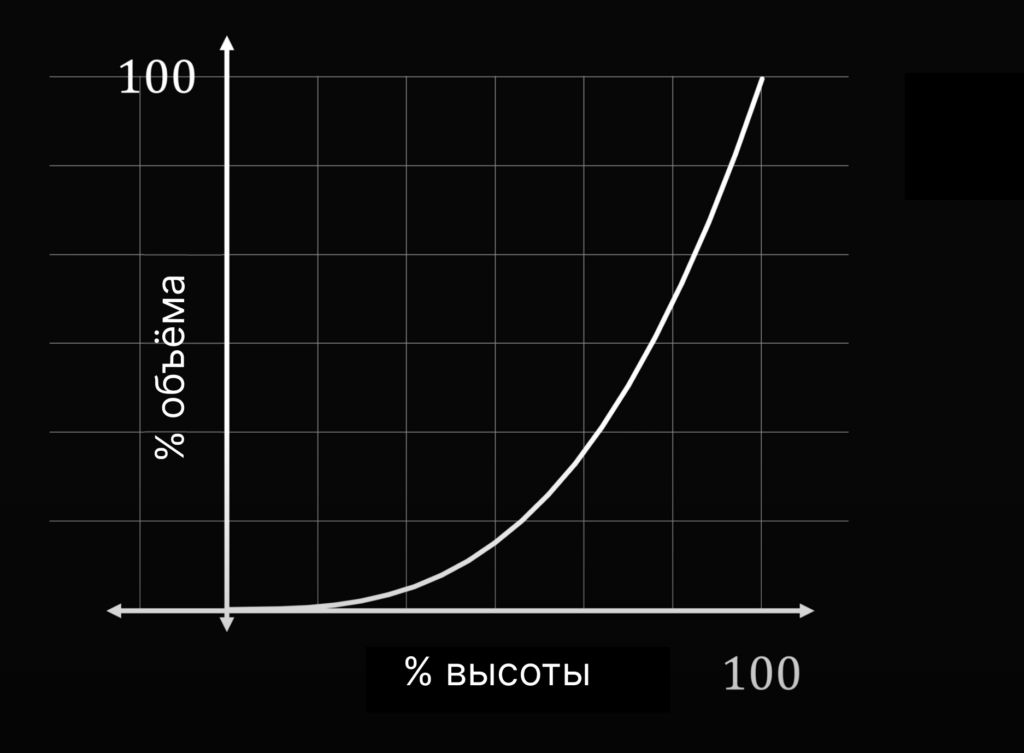
Поскольку 50% объёма — это 1/2, получаем равенство:
x3 = 1/2
x = 1/3√2
x = 0,794
Получается, что бокал можно считать наполовину полным (или пустым), если жидкость занимает около 80% высоты его чаши.
Если жидкость занимает 50% высоты чаши бокала, то бокал полон только на 12,5% (или пуст на 87,5%). Нужно восемь таких бокалов, чтобы получить полный бокал, если слить жидкость в один.
Если жидкость занимает 60% высоты чаши бокала, то бокал полон только на 21,6% (или пуст на 78,4%). Нужно пять таких бокалов, чтобы получить полный бокал.
Если жидкость занимает 70% высоты чаши бокала, то бокал полон только на 34,3% (или пуст на 65,7%). Нужно около трёх таких бокалов, чтобы получить полный бокал.
Теперь ходим в бар только с линейкой.