Самые странные, хитрые и неожиданные задачи про программистов и для программистов

Начнём с самого очевидного решения. Пусть Андрей и Вова поедут на мопеде, а Саша идёт пешком. Когда Андрей с Вовой доберутся до Мышкина, Андрей оставит там Вову и поедет обратно, в сторону Москвы, чтобы забрать Сашу:

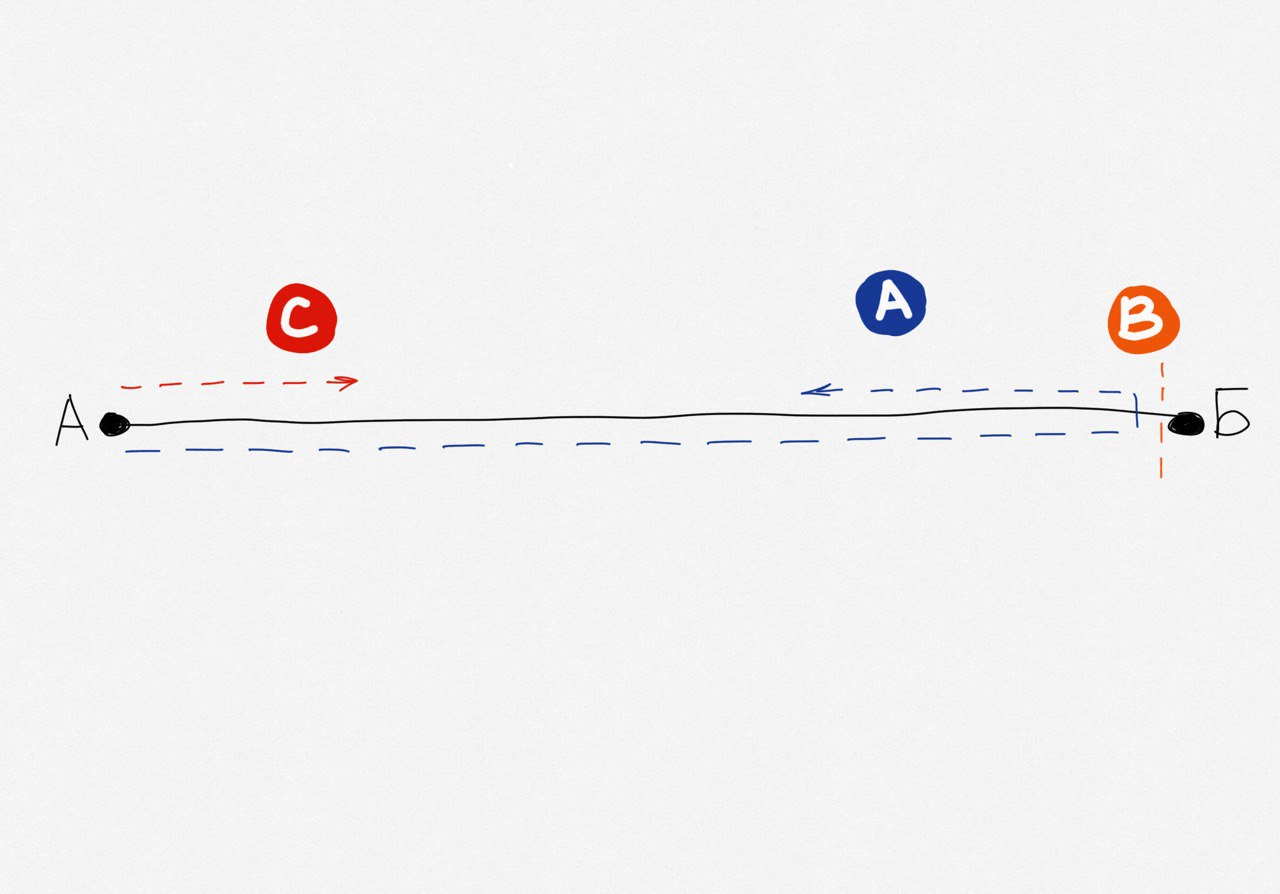
Это решение не самое оптимальное: пока Вова будет дожидаться Андрея с Сашей, он будет зря терять время и не внесёт никакого вклада в сокращение общего времени на дорогу. И если кто-либо из ребят будет ждать остальных, общее время не будет самым коротким.

Чтобы Вова мог поучаствовать в оптимизации времени, Андрею нужно оставить его недалеко от Мышкина. Тогда оставшееся расстояние Вова преодолеет пешком:

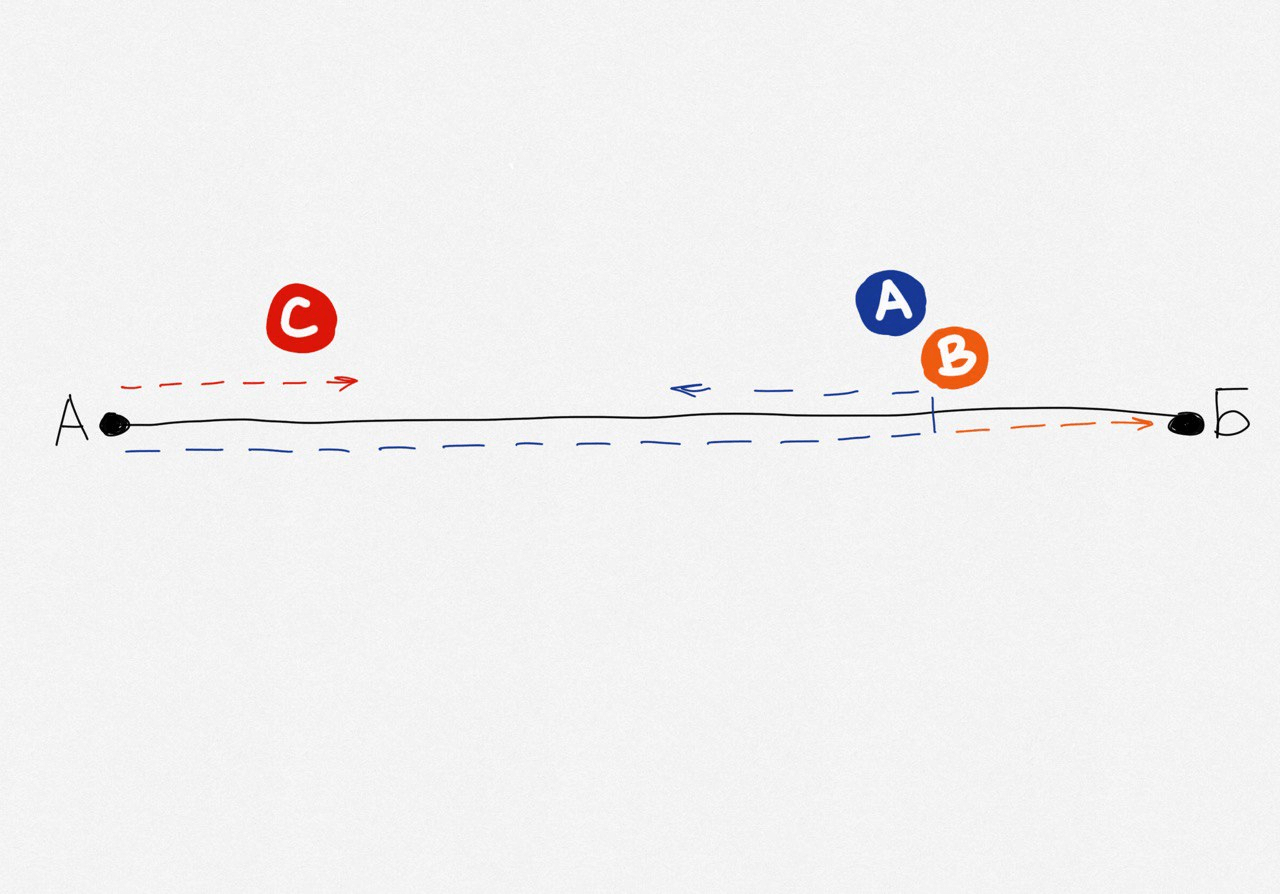
Как мы помним, общее время на дорогу может считаться самым коротким, если никто никого не дожидается. Если Вова доберётся раньше, он будет ждать Андрея с Сашей, а если позже, то Андрей и Саша будут ждать Вову.

Значит, нужно сделать так, чтобы Андрей с Сашей добрались до Мышкина одновременно с Вовой. Для этого нужно точно рассчитать точку на общем пути, где Андрей оставит Вову:

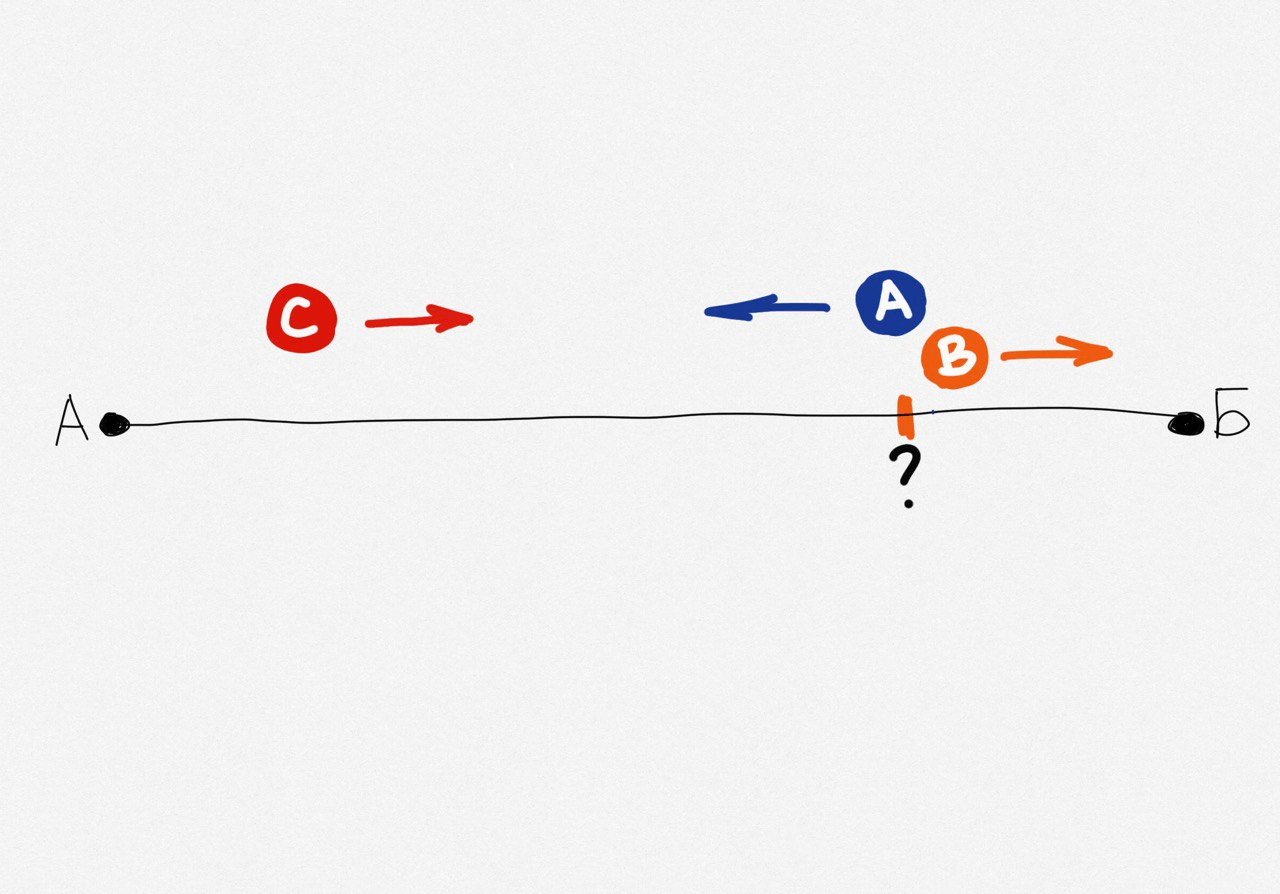
Теперь визуализируем весь план передвижений. Возьмём за А точку старта, за Б — точку финиша. В точке В₁ Андрей оставит Вову. В это время Саша будет в точке С₁. В точке С₂ его подберёт Андрей, а Вова в этот момент достигнет точки В₂: 

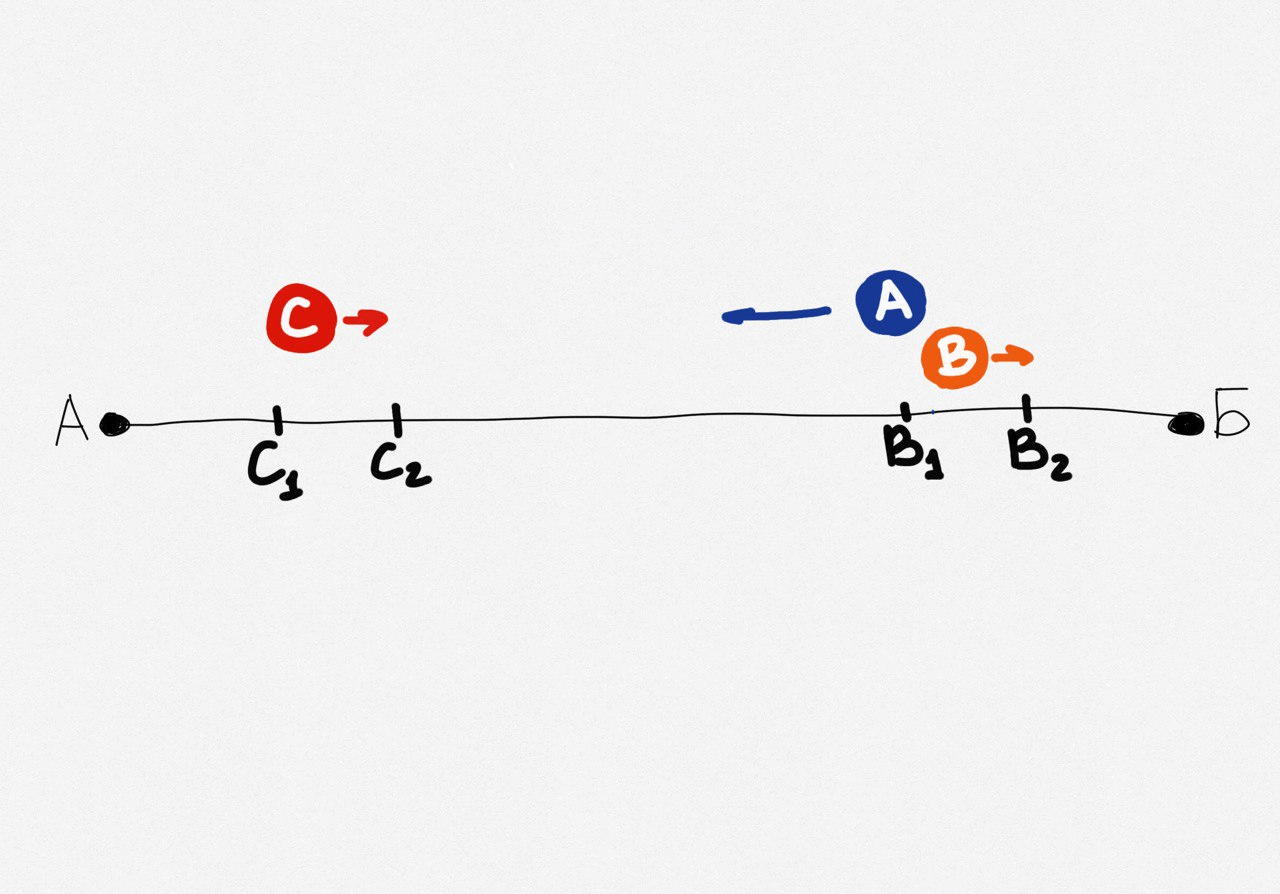
Теперь возьмём за t время, за которое Андрей вернётся на мопеде из точки В₁ на точку С₂, а расстояние от В₁ до С₂ возьмём за р:

t = В₁С₂/60 = р/60

За такое же время t Саша дойдёт из точки С₁ до точки С₂ (расстояние между ними возьмём за п):

t = С₁С₂/15 = п/15

За это же время t Вова дойдёт от точки В₁ до В₂:

t = В₁В₂/15

Так как в двух последних уравнениях у нас одинаковое время t и одинаковая скорость 15 км/ч, получается, что расстояние от С₁ до С₂ и от В₁ до В₂ — одинаковое:

t = п/15

Теперь на основании равенства времени t сравним расстояния р и п:

п/15 = р/60

р = 4п

Получаются такие отрезки:

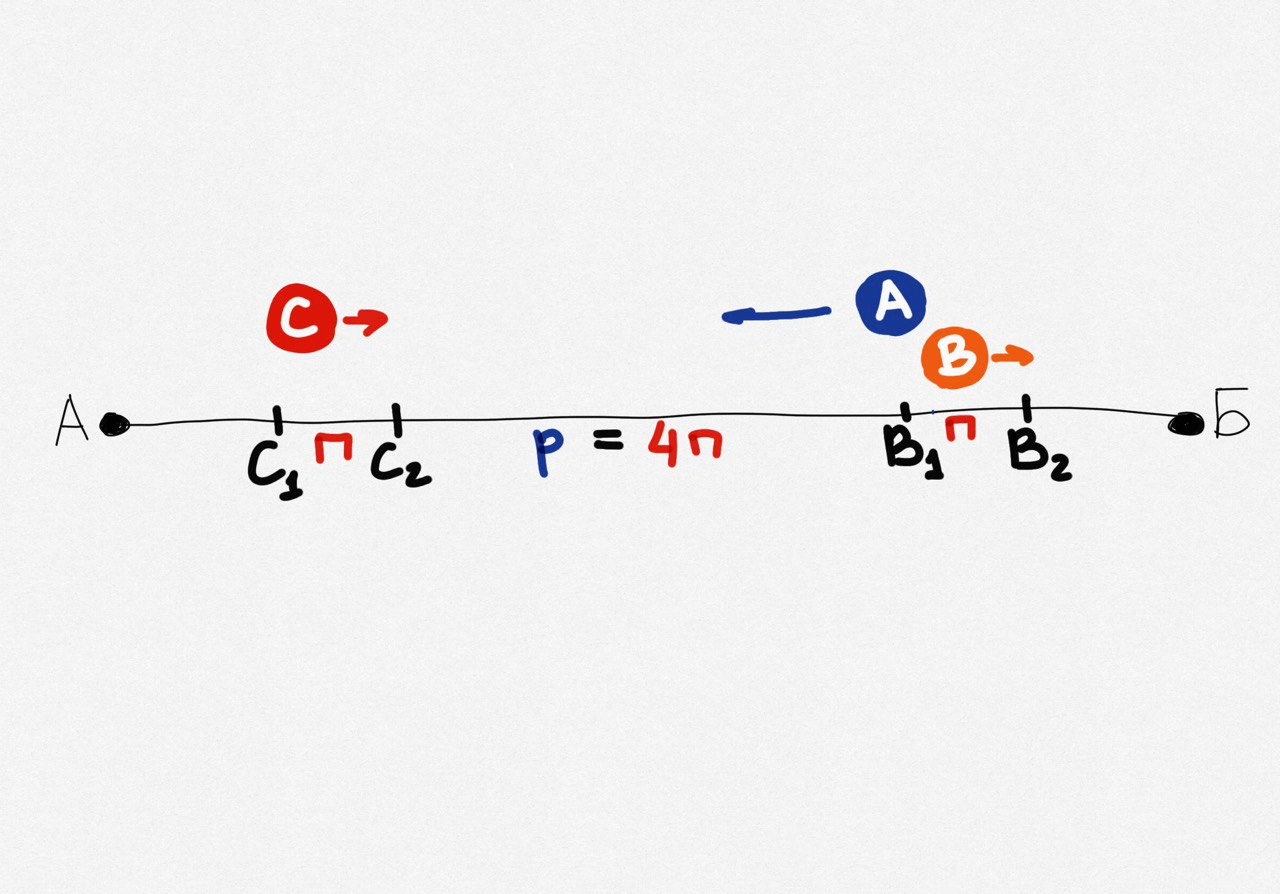
Теперь рассчитаем расстояние о, которое Вове останется пройти из точки В₂ до Б. Время, за которое Андрей и Саша проедут расстояние 4п + п + о, будет равно времени, за которое Вова дойдёт расстояние о:

(4п + п + о)/60 = о/15

о = (5/3)п

Теперь наш план перемещений выглядит так:

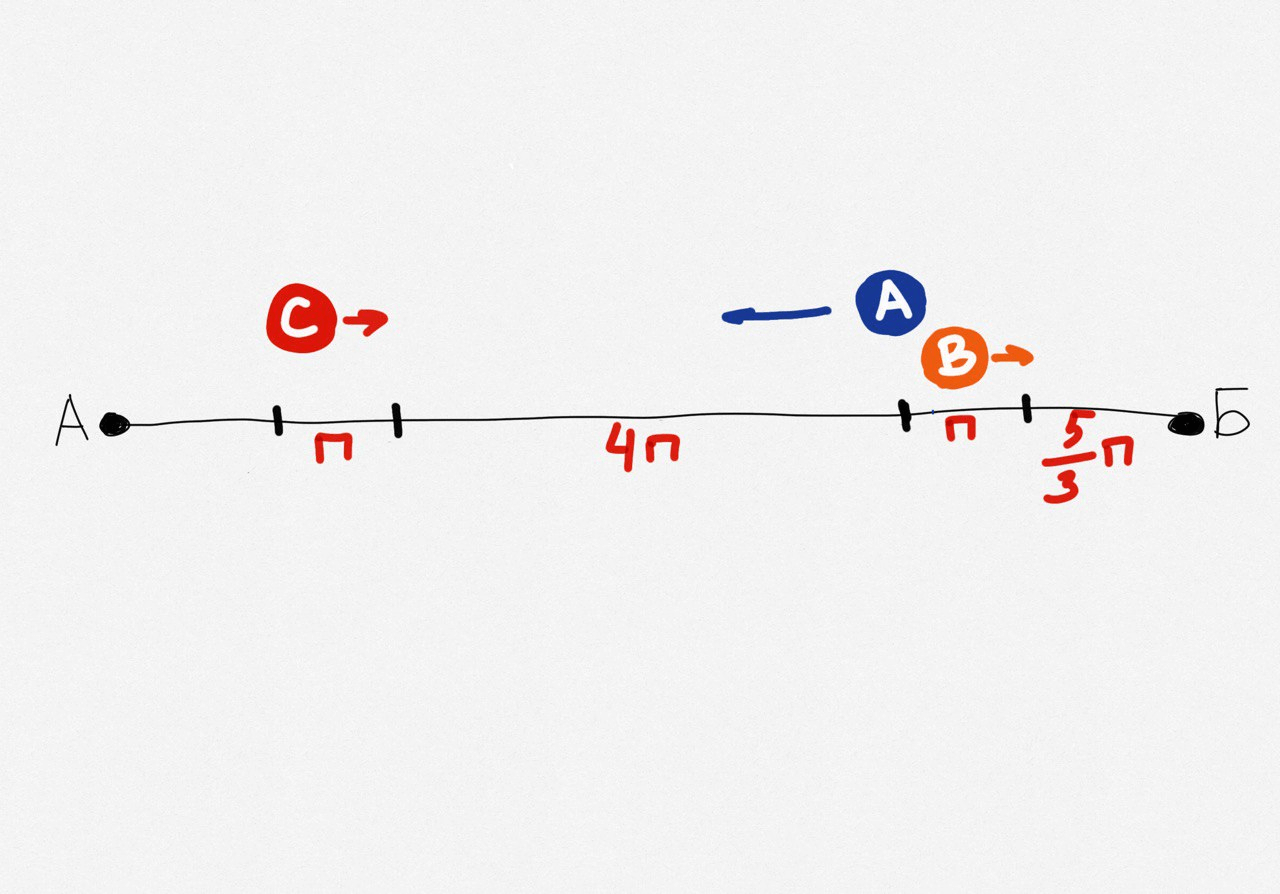
Нам осталось рассчитать расстояние н от точки старта А до С₁. У нас снова получается равенство времени, за которое Саша дойдёт до точки C₁, а Андрей с Вовой — доедут до точки В₁:

н/15 = (н + п + 4п)/60

н = (5/3)п

Ещё раз визуализируем все пути:

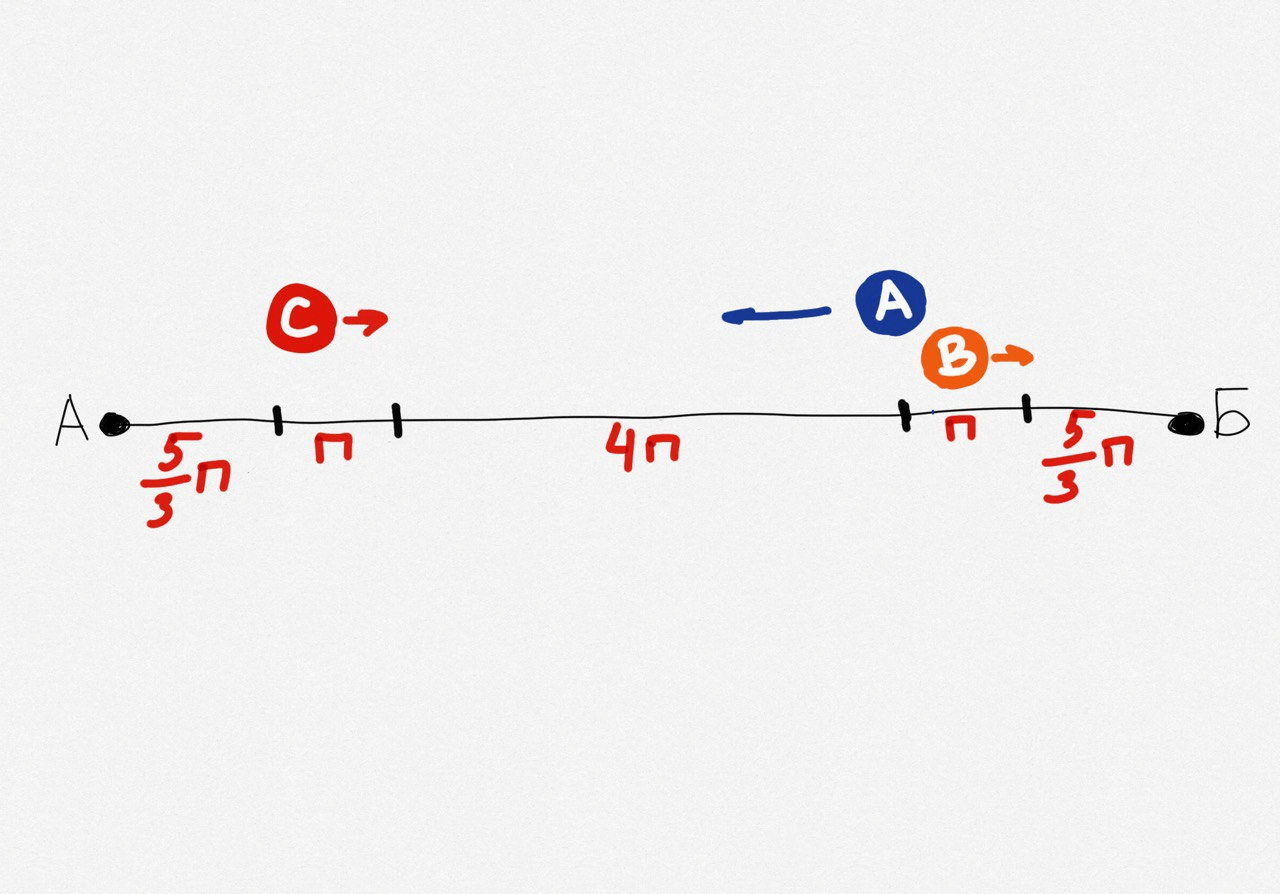
Получается такое равенство:

(5/3)п + п + 4п + п + (5/3)п = 300 км

п = 32,14 км

Подставим это значение в нашу визуализацию:

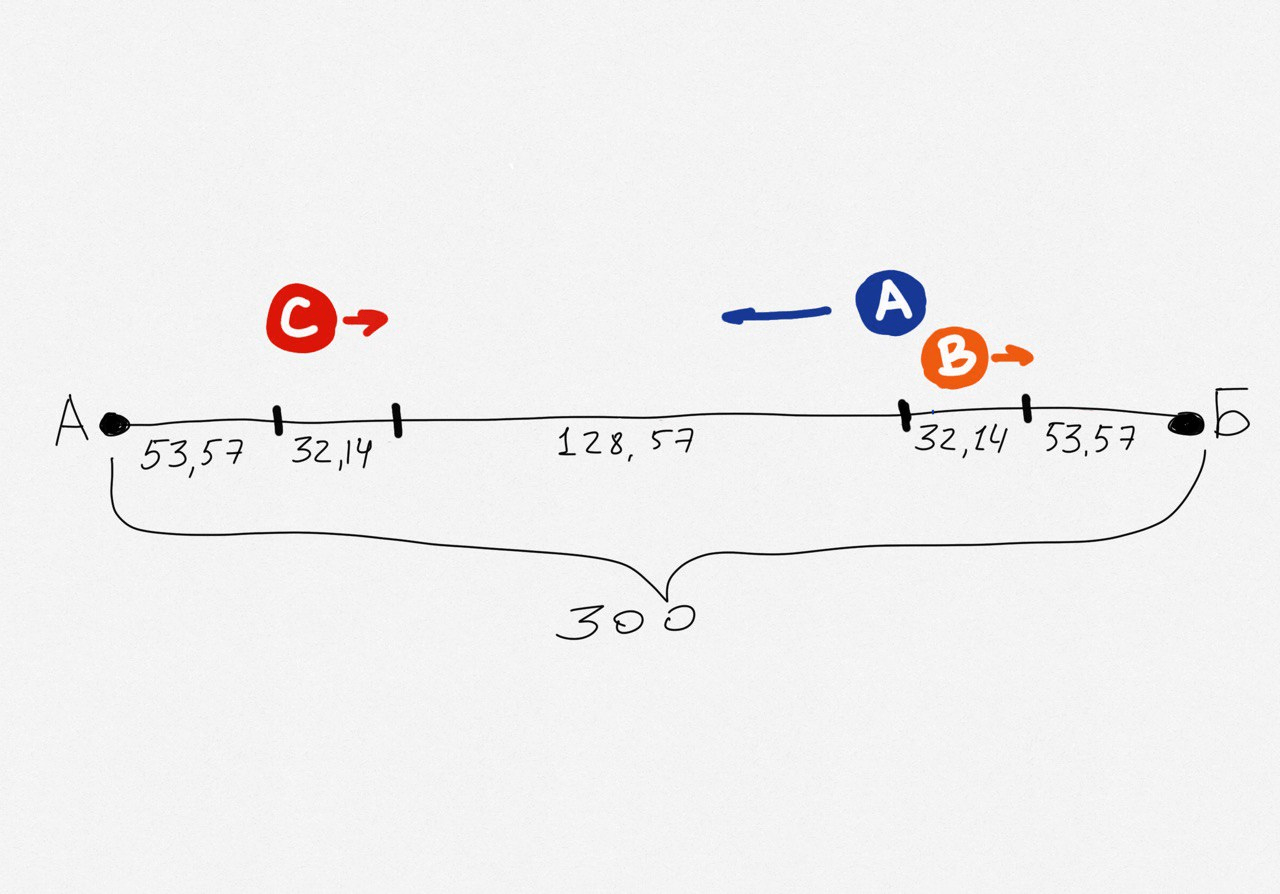
Теперь посчитаем самое короткое время, за которое все три айтишника доберутся из точки старта А до точки финиша Б. Посчитаем на примере Вовы:

t(Вова) = t(АВ₁) + t(о)

t(Вова) = АВ₁/60 + о/15

t(Вова) = 214,28/60 + 85,71/15

t(Вова) = 9,28 часа = 9 часов 17 минут

Получается, что самое короткое время составит примерно 9 часов, 17 минут.

Это задача про вероятности, поэтому вспомним основное:

Вероятность наступления какого-то события равна отношению количества нужных нам событий к общему количеству событий.

Например, вероятность выкинуть кубик с чётным числом очков считается так:

Теперь вернёмся к задаче.

Обозначим за Ах количество месяцев, которые должны пройти до того, как все джуны станут мидлами, где х — количество мидлов. В нашем случае у нас должно стать 6 мидлов, поэтому х = 6. Нам надо найти А0 — стартовую точку, которая покажет нам, сколько месяцев должно пройти, прежде чем все 6 станут мидлами.

Мы будем решать эту задачу в обратном порядке, поэтому следите за логикой.

Когда все джуны стали мидлами, это ситуация А6 — у нас 6 мидлов, а значит, 0 джунов. Получается, что А6 = 0, потому что все уже стали мидлами и не нужно ждать очередного месяца.

Теперь шагнём назад и посмотрим на ситуацию А5, когда у нас 5 мидлов и 1 джун. Вероятность того, что у нас через месяц джун станет мидлом — ½, либо станет, либо нет (и мы останемся в состоянии А5). Это значит, что количество месяцев, которое пройдёт, прежде чем этот джун станет мидлом равна:

А5 = 1 + ½ × А6 + ½ × А5, а единица здесь отвечает за месяц, который должен пройти, прежде чем любой джун станет мидлом.

Решим это уравнение. Мы выяснили, что А6 = 0, поэтому:

А5 = 1 + 0 + ½ × А5

А5 = 1 + ½ × А5 → А5 = 2

Откатимся ещё назад и посчитаем ожидаемое количество месяцев, до финала, когда у нас 4 мидла и 2 джуна — это А4. Сейчас распишем подробно решение, чтобы была понятна логика на следующих этапах.

У нас 2 джуна, каждый из которых может стать мидлом (а может и не стать). Получается, у нас 4 исхода месяца:

Зная это, получим формулу:

А4 = 1 (прошёл месяц) + ¼ × А6 (оба стали мидлами) + 2/4 × А5 (один стал, а другой нет) + ¼ × А4 (оба не стали)

А4 = 1 + ¼ × А6 + 2/4 × А5 + ¼ × А4 ← подставим сюда уже известные значения А6 и А5

А4 = 1 + 0 + ½ × 2 + ¼ × А4

А4 = 8/3

Откатимся снова и получим ситуацию, когда у нас 3 мидла и 3 джуна — это ситуация А3. Всего у нас может быть 8 исходов, когда кто-то становится мидлом, а кто-то нет (2³ = 8) и 4 возможных исхода:

Запишем это в виде уже привычной формулы:

А3 = 1 + ⅛ × А6 + ⅜ × А5 + ⅜ × А4 + ⅛ × А3

Подставим уже известные значения А6, А5 и А4 и получим значение А3:

А3 = 22/7

Снова откатываемся назад и смотрим на ситуацию А2, когда у нас 2 мидла и 4 джуна. Теперь у нас 2⁴ = 16 возможных ситуаций и 5 разных исходов:

Составим формулу для А2 и потом подставим уже известные значения А6 — А3:

А2 = 1 + 1/16 × А6 + 4/16 × А5 + 6/16 × А4 + 4/16 × А3 + 1/16 × А2

А2 = 368/105

Откатимся ещё на шаг назад и посмотрим на ситуацию А1, когда у нас 1 мидл и 5 джунов. Здесь 2⁵ = 32 возможных ситуаций и 6 возможных ситуаций:

Составим формулу для А1 и потом подставим уже известные значения А6—А2:

А1 = 1 + 1/32 × А6 + 5/32 × А5 + 10/32 × А4 + 10/32 × А3 + 5/32 × А2 + 1/32 × А1

А1 = 2470/651

И наконец, откатимся до стартового условия, когда у нас 0 мидлов и 6 джунов — то, что нам и нужно найти. Здесь 2⁶ = 64 возможных ситуации и 7 возможных исходов:

Составим формулу для А0 и потом подставим уже известные значения А6—А1:

А0 = 1 + 1/64 × А6 + 6/64 × А5 + 15/64 × А4 + 20/64 × А3 + 15/64 × А2 + 6/64 × А1 + 1/64 × А0

А0 = 7880/1953 ≈ 4,03

Получается, что ожидаемое время, когда все 6 джунов станут мидлами — 4,03 месяца. Но так как повышение происходит каждый месяц, нужно округлить до 5. Но это не значит, что через 5 месяцев все ТОЧНО станут мидлами — это лишь среднее значение вероятности, что скорее всего это произойдёт через это время.

Уф. Решили. Вы — крутые, если дочитали досюда.

Представим нашу задачу визуально. До первого обхода программиста все сто дверей закрыты:

В первый обход программист меняет состояние каждой двери, то есть открывает их:

Во второй обход он закрывает все двери с номером, кратным двум, то есть каждую вторую: 2, 4, 6, 8, 10, 12 и так далее.

В третий обход он закрывает или открывает все двери с номером, кратным трём, — каждую третью: 3, 6, 9, 12, 15, 18 и так далее.

Попробуем порассуждать и для примера возьмём дверь с номером 50. Поскольку число 50 кратно числам 1, 2, 5, 10, 25 и 50, получается, что программист коснётся этой двери в первый, второй, пятый, десятый, двадцать пятый и пятидесятый обходы. Вот как будет меняться состояние двери:

Получается, что двери, которых программист коснётся чётное число раз, после сотого обхода останутся закрытыми. А двери, которых программист коснётся нечётное число раз, останутся открытыми.

Проанализируем эту ситуацию и выведем закономерность. Дверь с номером 50 будет открыта и закрыта за шесть обходов:

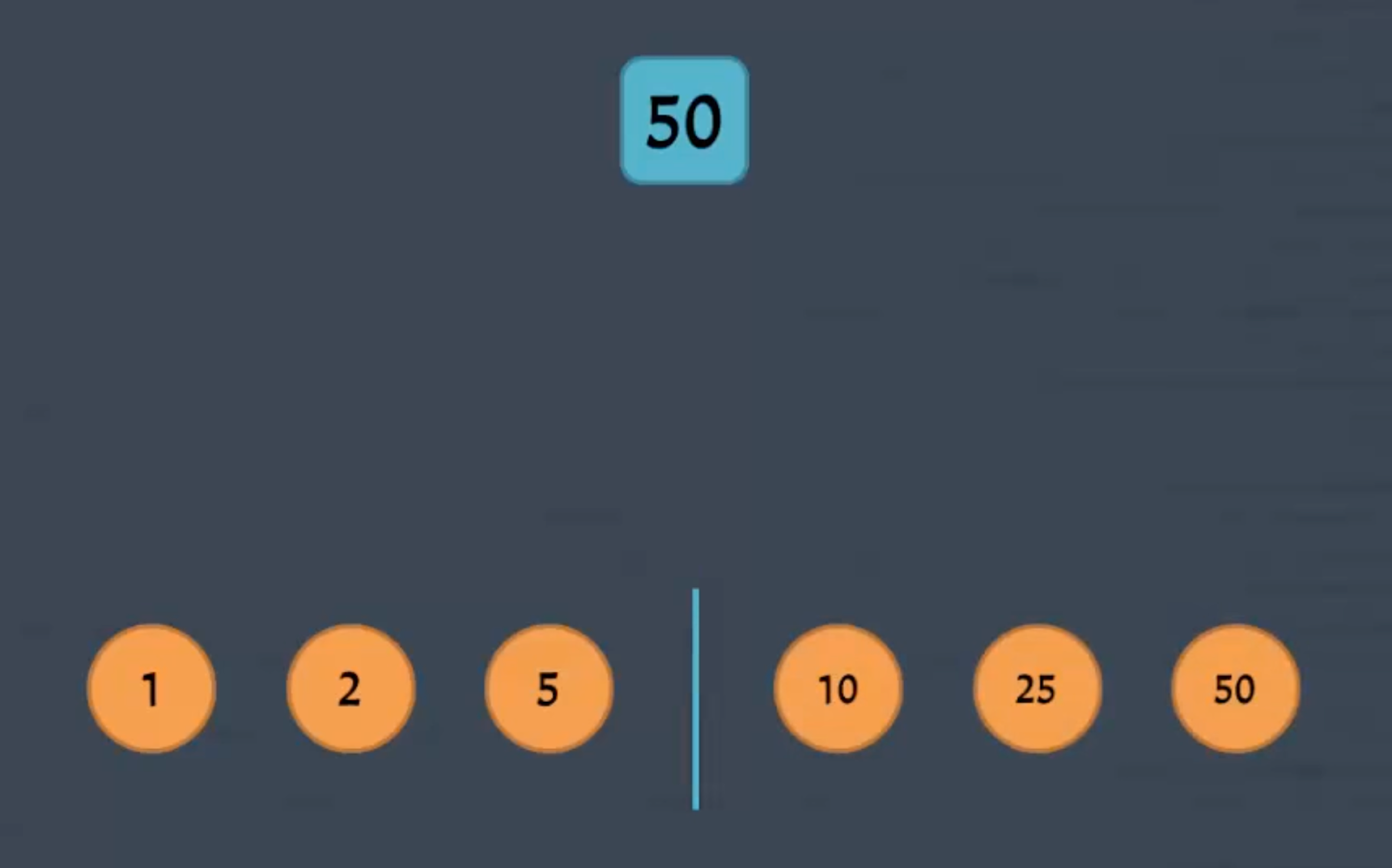
При умножении номеров первого и последнего, второго и предпоследнего и третьего и четвёртого обходов мы получим число номера двери — 50:

1 × 50 = 50

2 × 25 = 50

5 × 10 = 50

Похожей будет закономерность для всех дверей, которых программист коснётся чётное число раз. А какой она будет для остальных дверей?

Представим дверь с номером X, которой программист коснётся нечётное число раз, например пять:

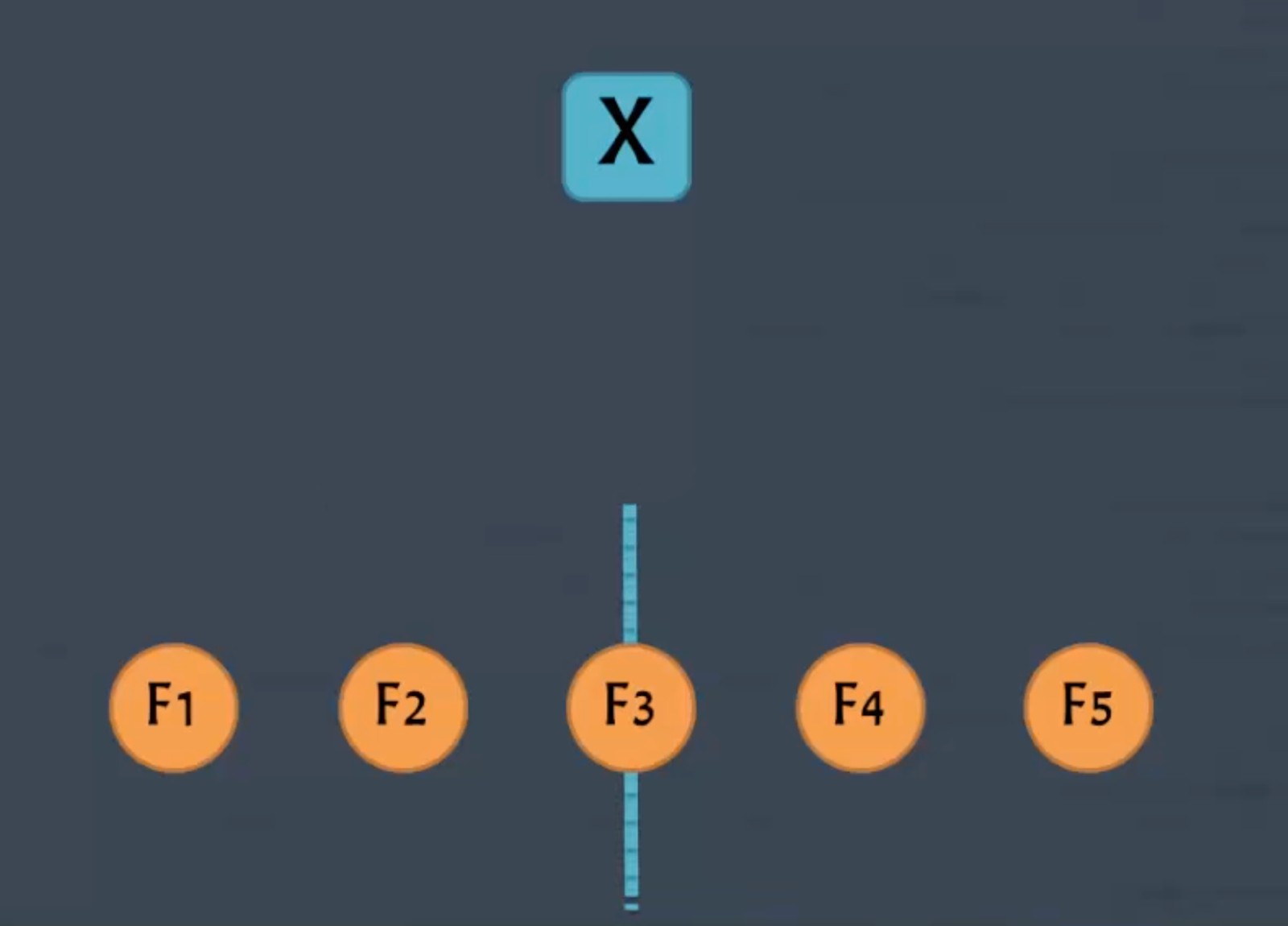
Получается, что для такой двери будут верны следующие уравнения:

F₁ × F₅ = X

F₂ × F₄ = X

F₃ × F₃ = X

Последнее уравнение получается квадратным:

F₃² = X

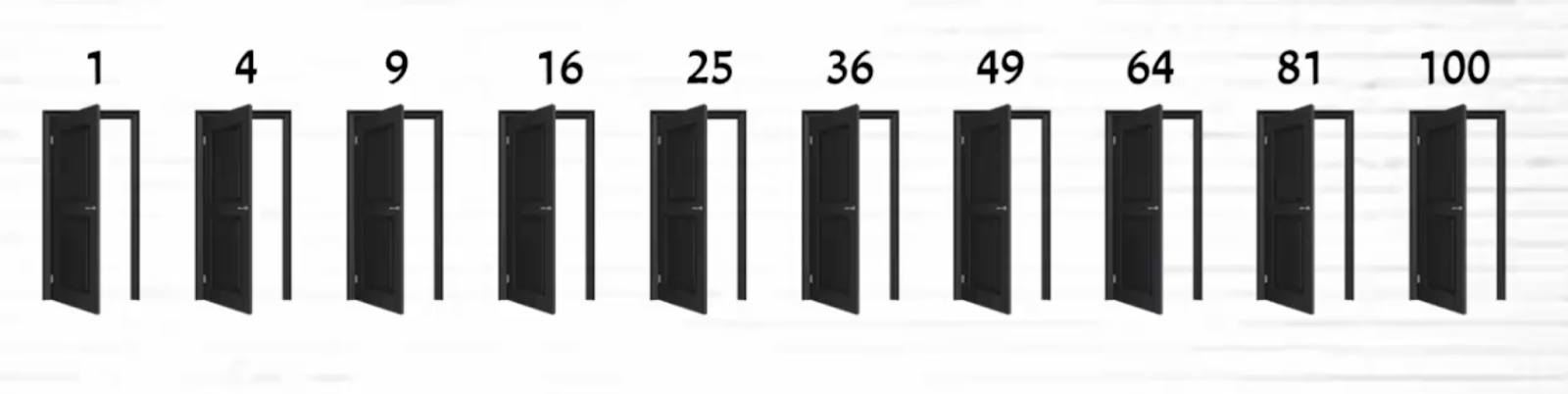
Из этого следует, что открытыми останутся двери, номера которых получаются из умножения номера обхода на него же: 

1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

Для решения на Python нам нужно будет учесть два момента:

Зная это, напишем простой код, который за нас пройдёт по 100 раз мимо всех дверей и откроет (1) и закроет их (0) по правилам из условия.

# создаём пустой список дверей
doors = []
# теперь создаём сто новых дверей
for i in range(100):
    # и делаем все их закрытыми
    doors.append(0)
# делаем 100 проходов
for i in range(1,101):
    # и в каждом проходе смотрим все двери
    for j in range(100):
        # если номер двери нацело делится на номер прохода
        if (j+1) % i == 0:
            # если она закрыта
            if doors[j] == 0:
                # открываем её
                doors[j] =  1
            # а если открыта
            else:
                # то закрываем 
                doors[j] = 0
# смотрим в итоге все двери, в каком они состоянии
for i in range(100):
    # если очередная дверь открыта
    if doors[i] == 1:
        # то выводим её номер
        print(i+1)

Сначала разберёмся с партиями и их количеством. На всякий случай поясним, что если Аня сыграла партию с Витей, то это значит, что каждый из них сыграл по одной партии:

Аня против Вити: 1 партия, при этом Аня сыграла одну партию и Витя тоже сыграл одну партию.

Это значит, что количество проведённых игр в два раза меньше, чем количество партий, которые получилось сыграть всем игрокам. В нашем случае было сыграно 8 + 12 + 14 = 34 индивидуальных партии, что даёт 34 / 2 = 17 партий всего.

Теперь посмотрим на Аню — она сыграла всего 8 партий из 17, при этом она точно начинала играть каждый раз, когда проигрывал кто-то из оставшихся ребят. Но единственный вариант, при котором это возможно, — если Аня начала играть со второй партии и проигрывала каждую игру. Например, начала со второй, проиграла её и пропустила третью, потом сыграла четвёртую, проиграла её и пропустила пятую и так далее:

Получается, мы только что нашли половину ответа: в четвёртой игре точно играла Аня и ещё кто-то. Кто — сейчас выясним.

Раз Аня играла во всех чётных играх, то Боря и Коля играли во всех нечётных. Но у Бори сыграно 12 партий, а у Коли — 14. При этом мы знаем, что Боря сыграл 7 последних партий подряд.

Распишем эти игры:

11 игра: Боря и Коля

12 игра: Боря и Аня (она играла все чётные игры)

13 игра: Боря и Коля

14 игра: Боря и Аня

15 игра: Боря и Коля

16 игра: Боря и Аня 

17 игра: Боря и Коля

Но до этого мы выяснили, что все нечётные игры были между Борей и Колей (потому что в нечётных играла Аня). Это значит, что Боря сыграл:

9 нечётных игр (1, 3, 5, 7, 9, 11, 13, 15, 17)

3 чётные игры (12, 14, 16)

Это в сумме даёт 12 партий — как раз столько и написано в условии задачи. А это значит, что в четвёртой партии он не мог принять участие и там играл Коля.

Выходит, что четвёртая партия была между Аней и Колей, и в ней победил Коля. 

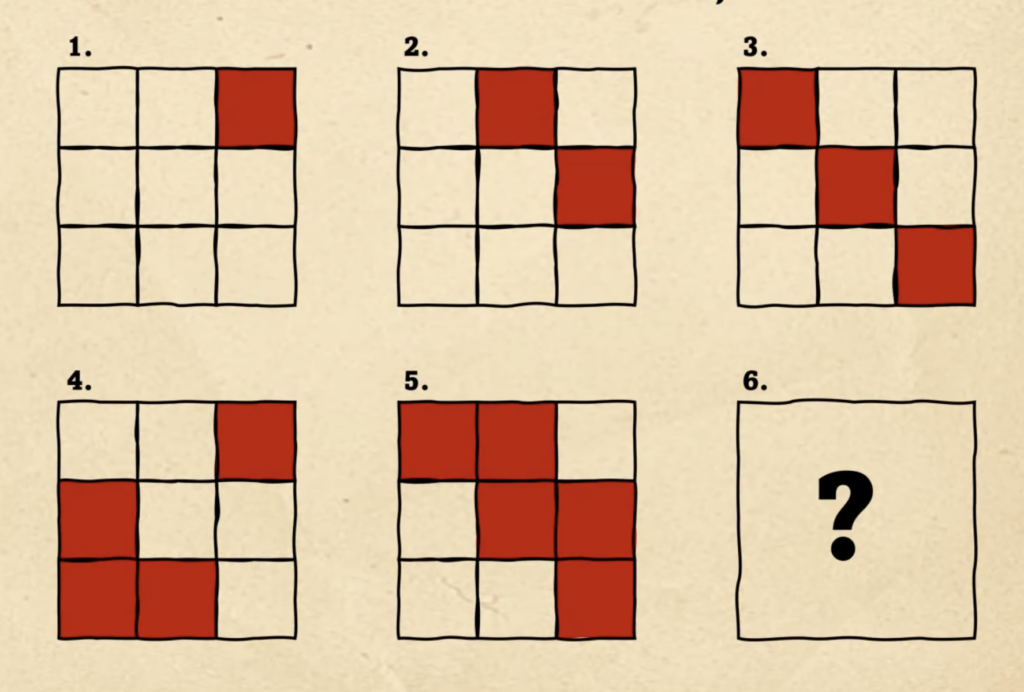
Первое, что можно заметить — что количество красных клеток в фигурах на каждом этапе увеличивается на единицу: на первом рисунке она одна, на втором две и так далее. Для наглядности поместим их рядом с фигурами:

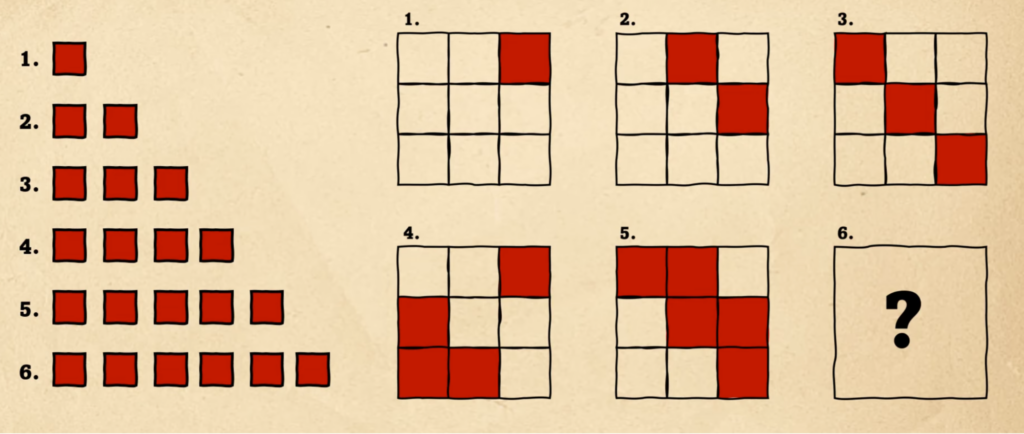
Дальше мы видим, что первые три фигуры заполняются красными клетками как бы по диагонали, слева направо. Используем это и расширим шаблон на все остальные клетки:

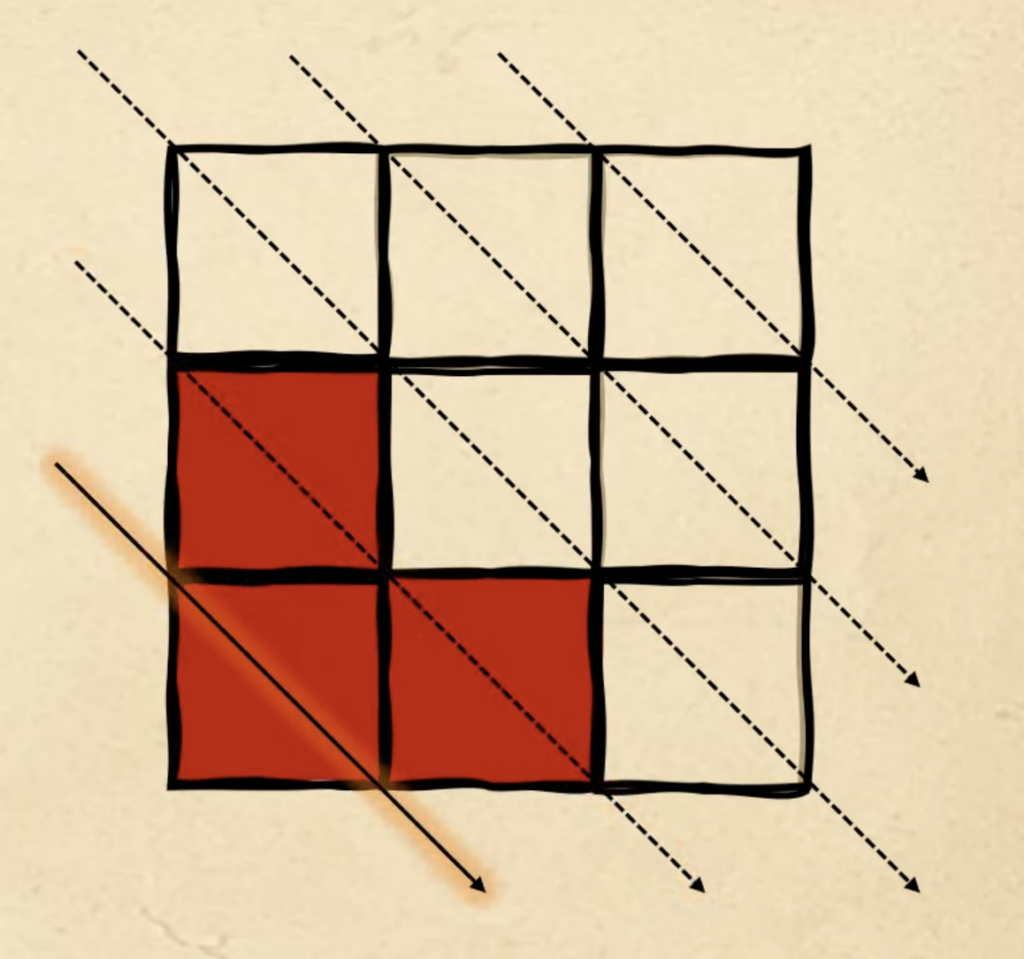
С первой фигурой всё просто — ставим красный квадрат ровно на первую диагональную линию:

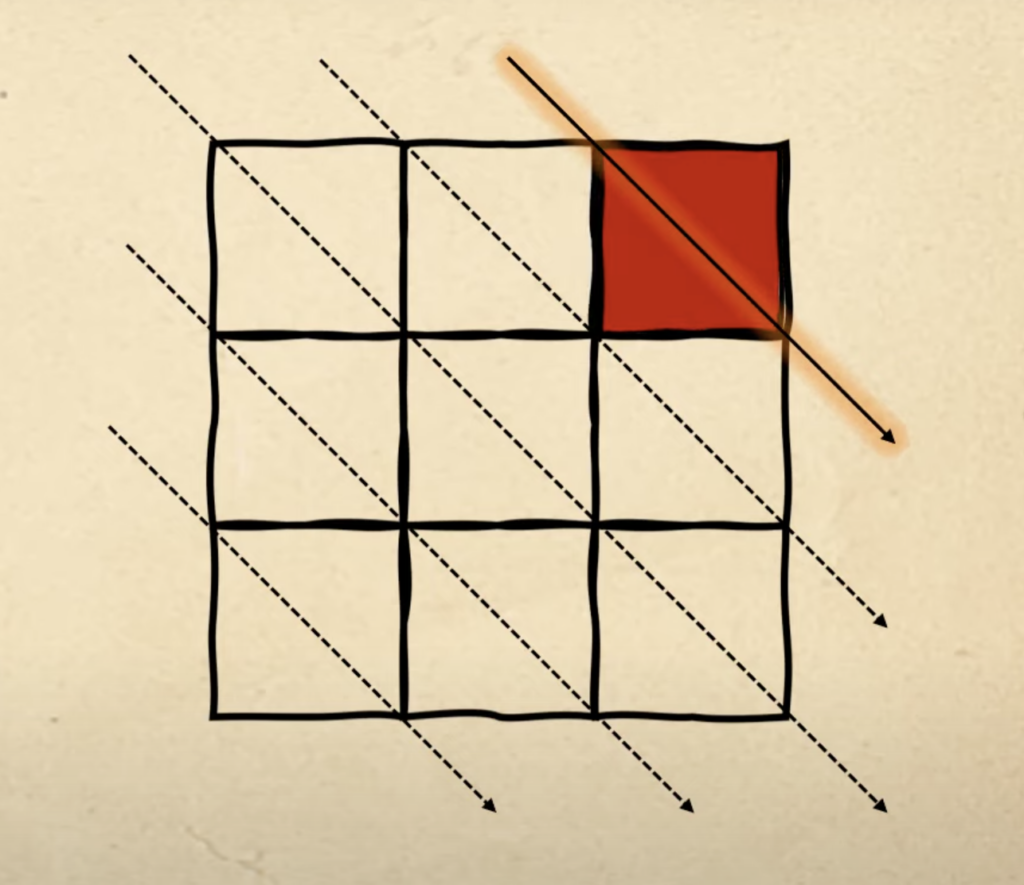
Следующая свободная диагональ, на которой мы закончили, — вторая, поэтому второй фигурой заполняем её:

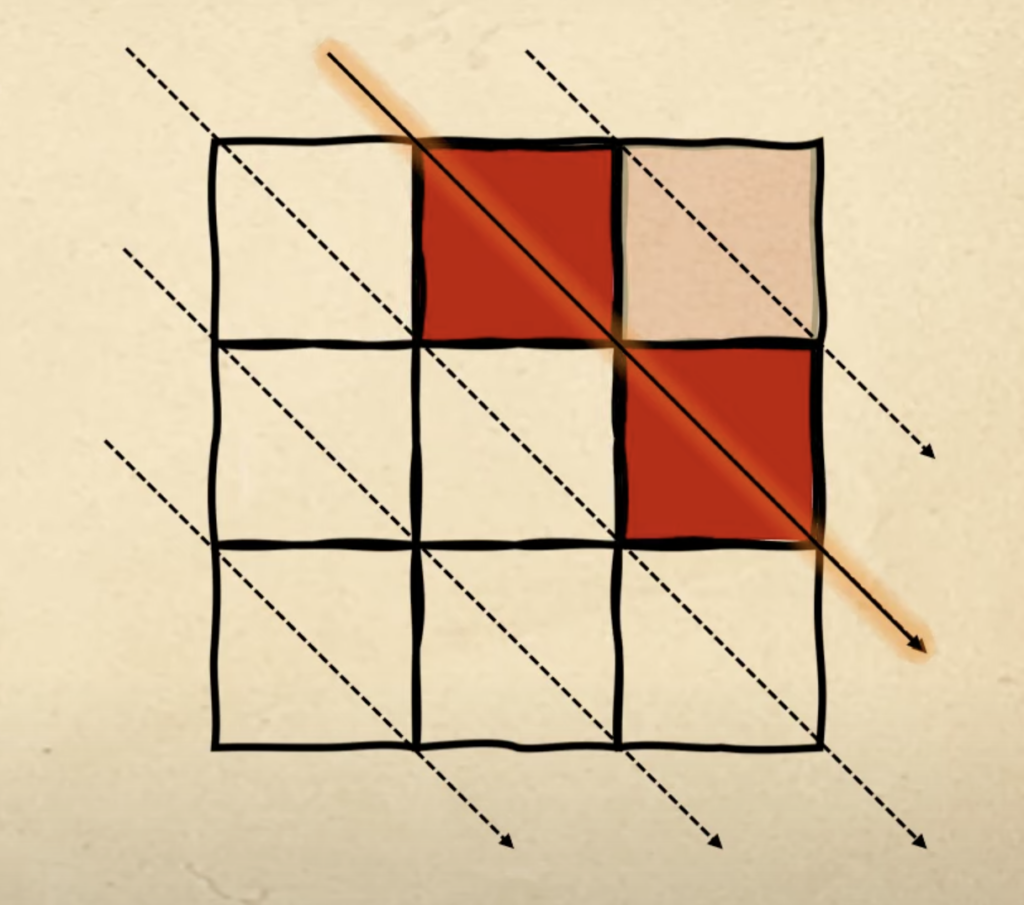
С третьей фигурой тоже всё удачно: мы закончили на второй диагонали, поэтому начинаем новую фигуру заполнять с третьей:

На прошлом шаге мы использовали третью диагональ, поэтому начинаем с четвёртой. Но с ней всё сложнее: на ней всего две клетки, а нам нужно разместить четыре красных квадрата:

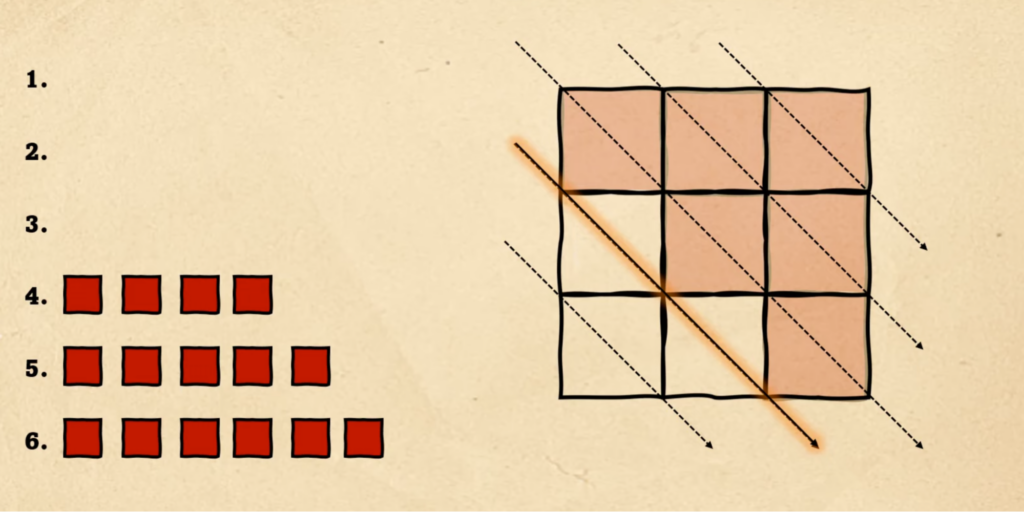
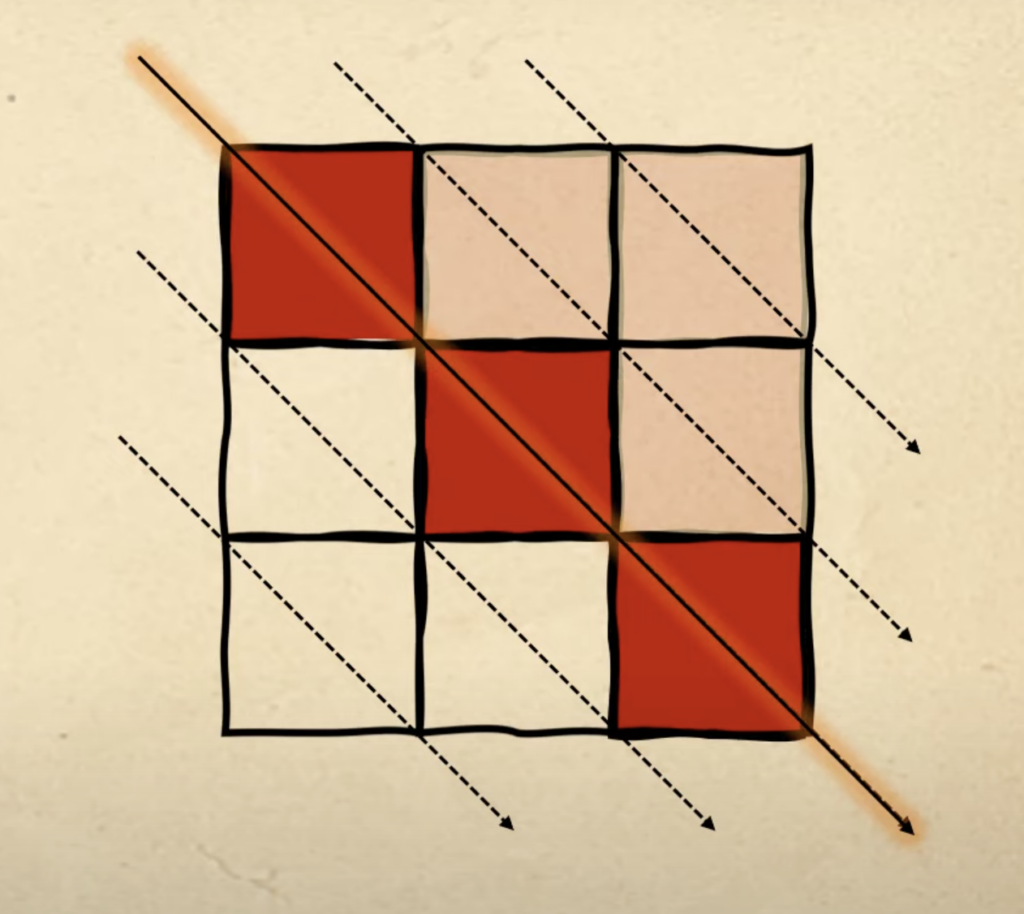
Тогда мы заполняем всю четвёртую диагональ двумя красными квадратами и переходим на пятую — туда, где станет всего один красный квадрат:

Но мы разместили на фигуре три красных квадрата, а нам нужно четыре. Возвращаемся к самому началу, к первой диагонали, и ставим туда четвёртый красный квадрат — в итоге получаем как раз нужную нам четвёртую фигуру:

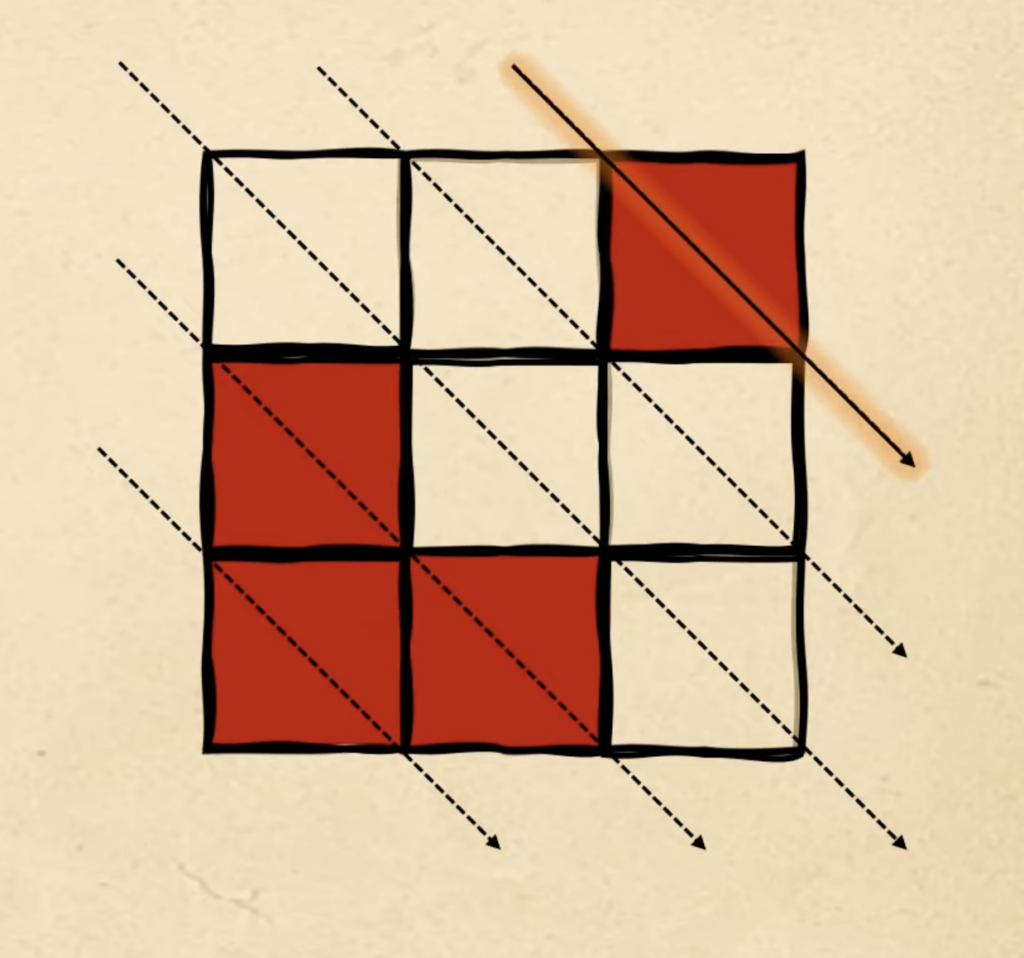
Раз мы пошли заполнять диагонали по второму кругу, придерживаемся того же принципа: начинаем с первой свободной диагонали, которую мы не использовали в прошлый раз. В четвёртой фигуре мы остановились на первой диагонали, поэтому в пятой фигуре начинаем со второй:

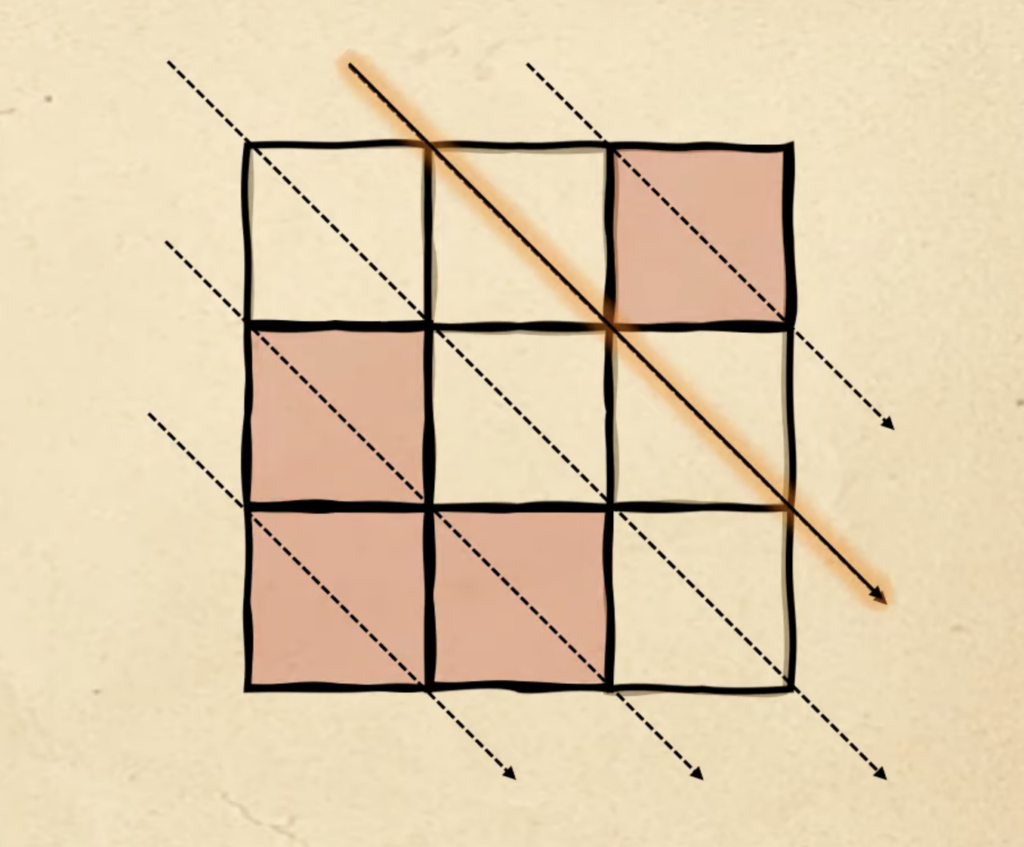
Ставим сюда два красных квадрата:

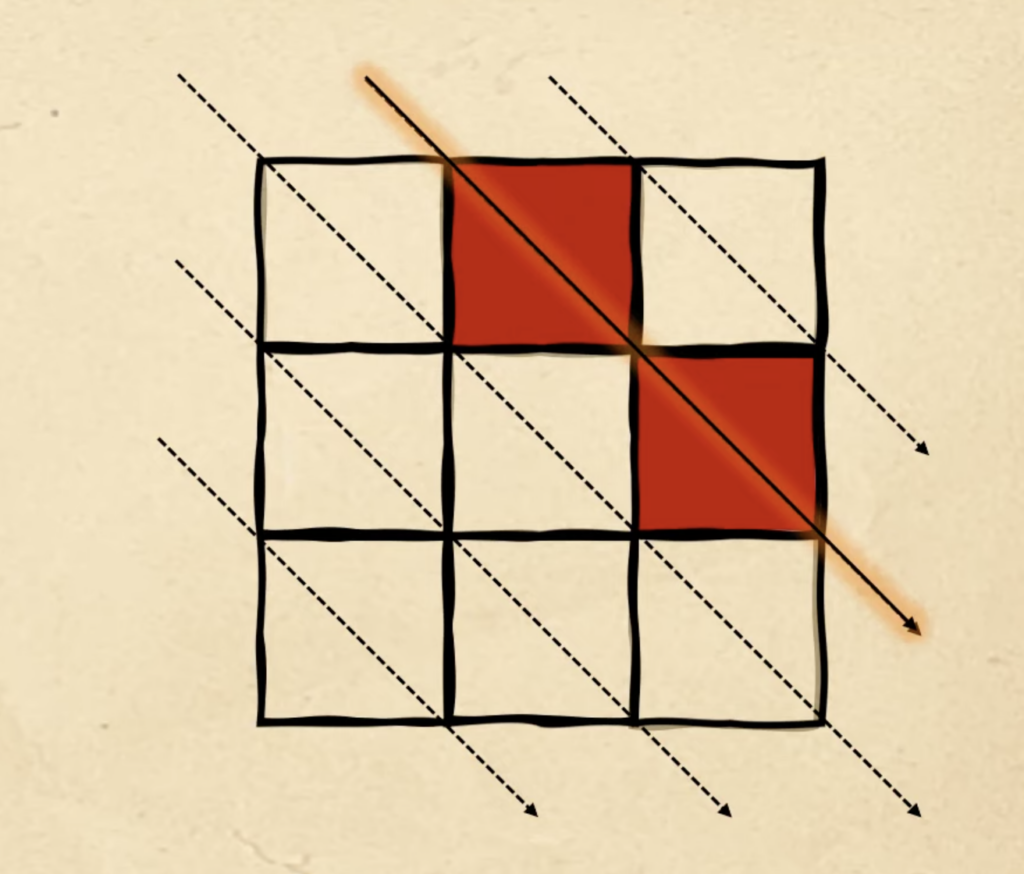
Нам нужно поставить пять квадратов, а у нас ещё осталось три. Переходим на следующую диагональ и заполняем там оставшиеся три красных квадрата — и получаем пятую фигуру из задачи:

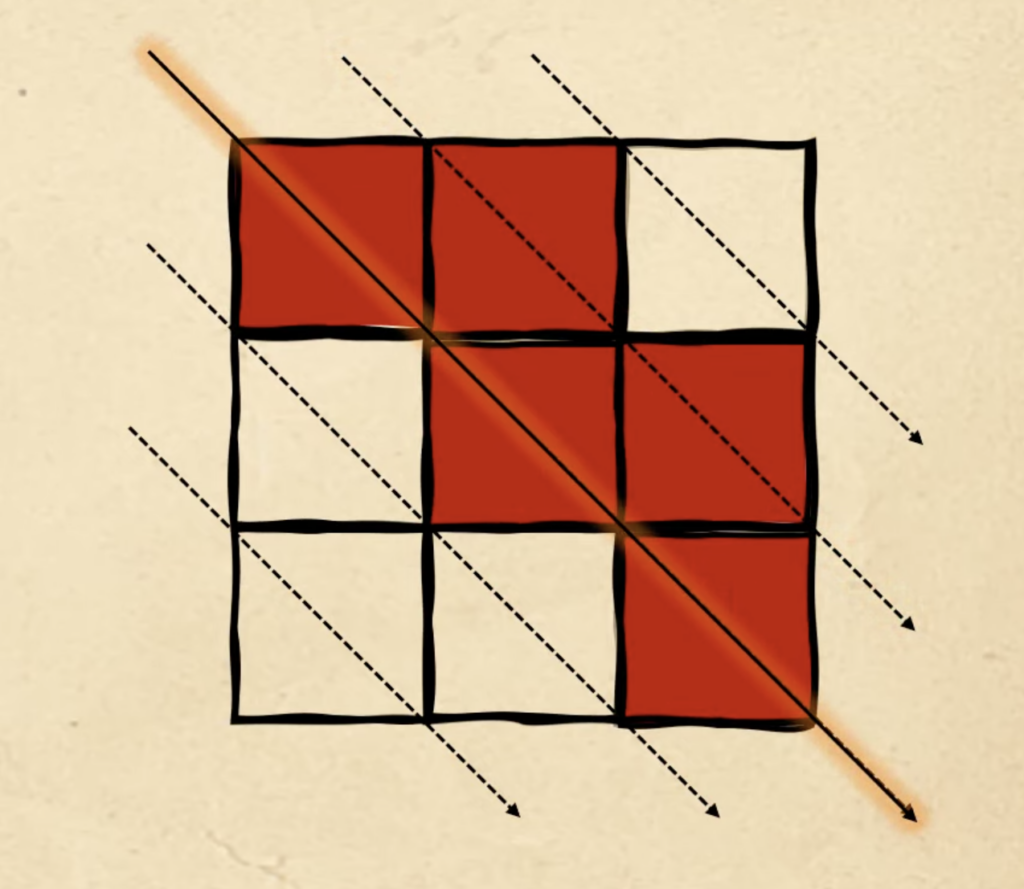
Наконец, переходим к шестой — той, что нам нужно найти. В пятой фигуре мы закончили на третьей диагонали, поэтому теперь начинаем с четвёртой:

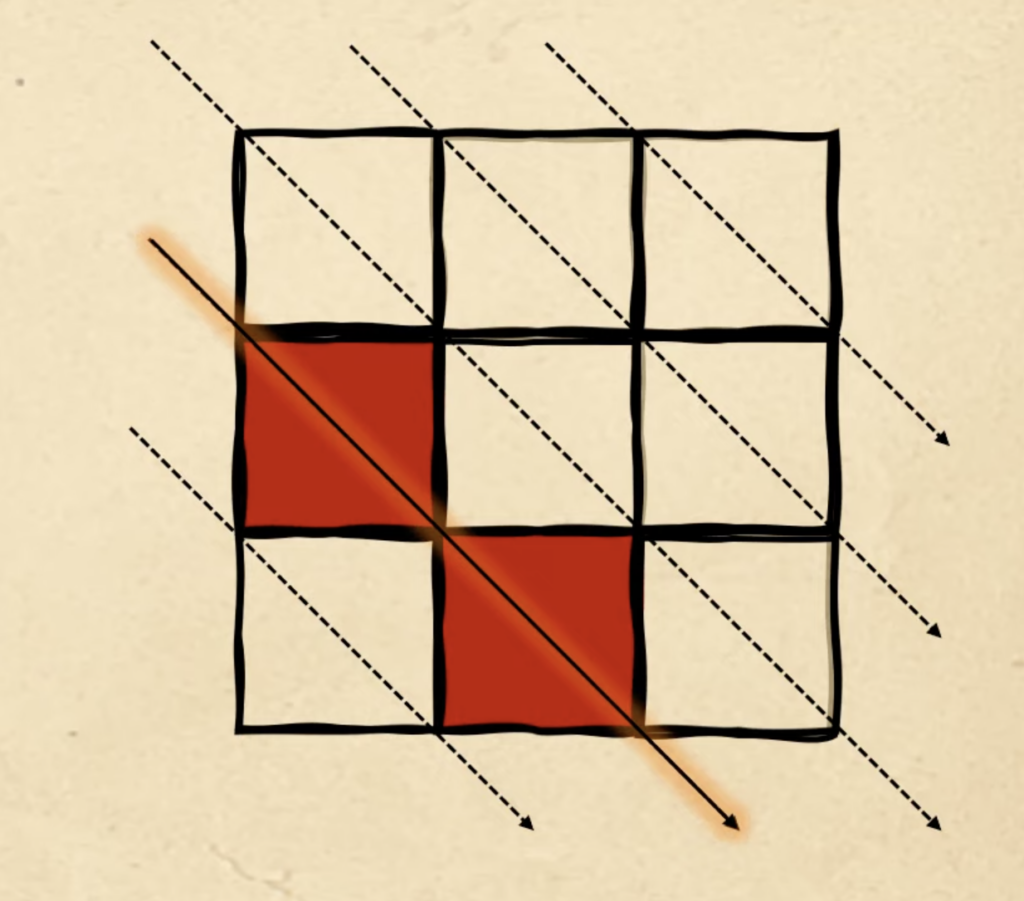
По этому же алгоритму заполняем пятую диагональ:

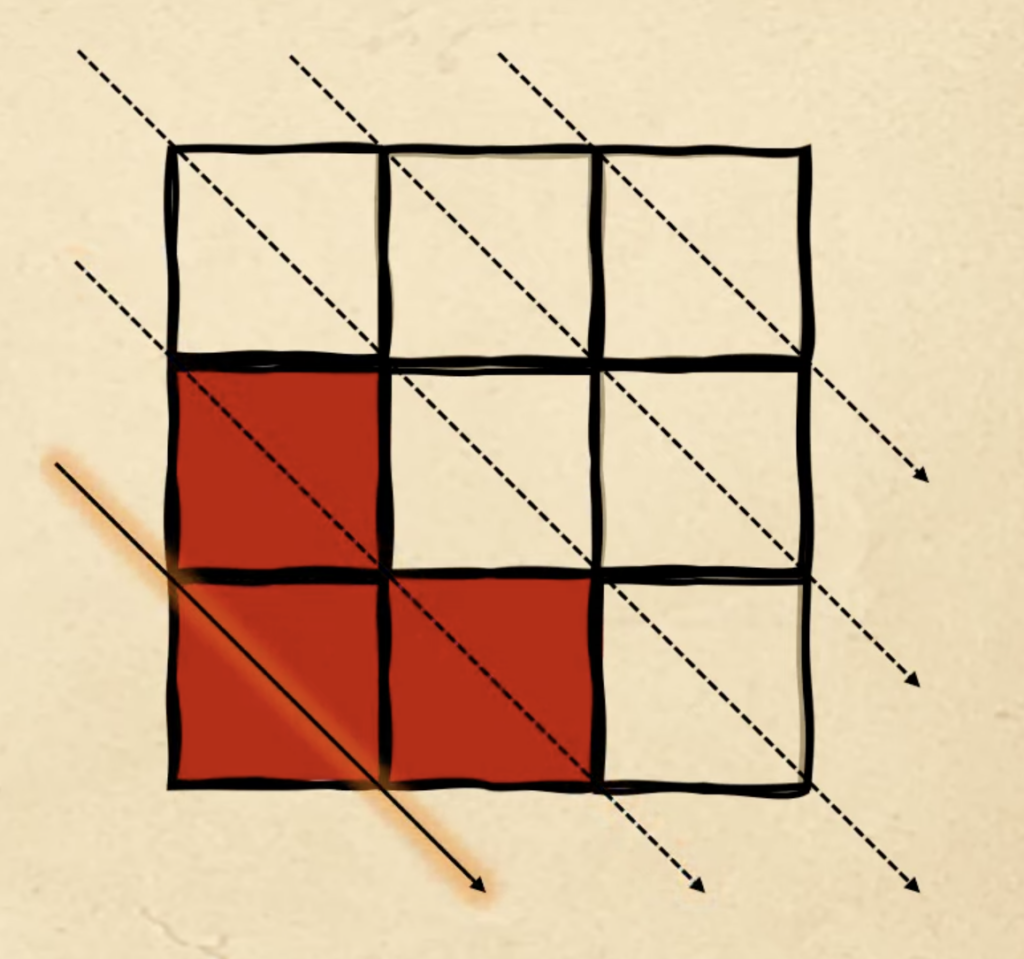
Но у нас ещё есть три красных квадрата, поэтому возвращаемся снова к первой диагонали и начинаем заполнять их оттуда:

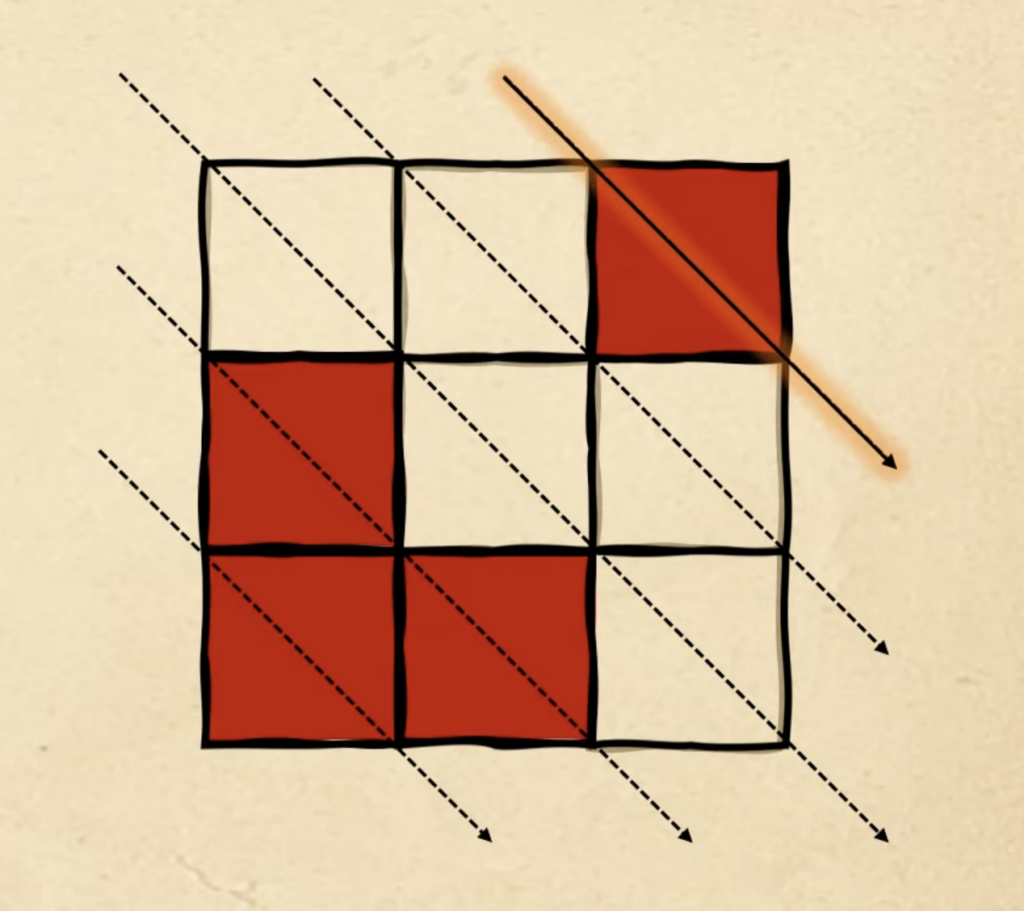
И в завершение используем вторую диагональ, чтобы поставить оставшиеся два красных квадрата. Это и будет шестая фигура:

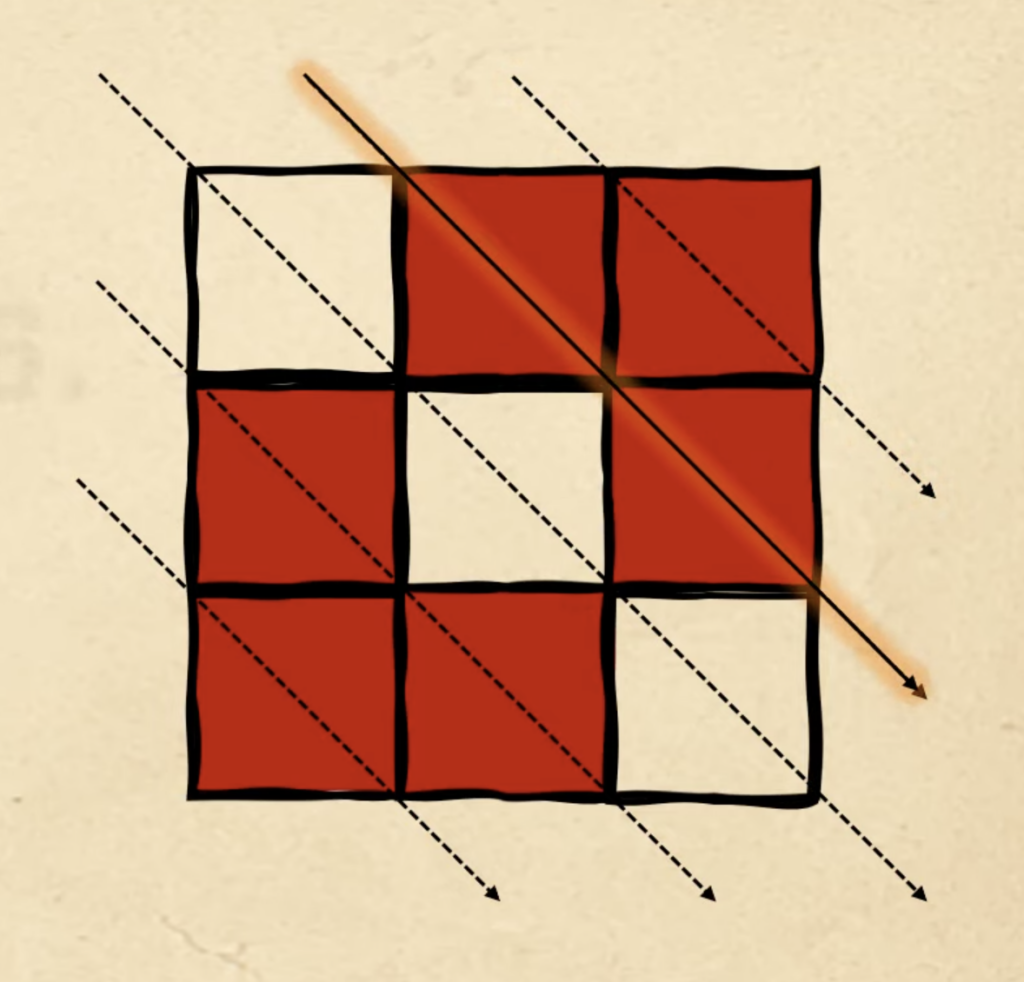
Теперь, когда вы решили задачу и поняли алгоритм, попробуйте найти 7-ю, 8-ю и 9-ю фигуру и поделитесь результатами в комментариях.

Начнём с того, что разделим наши скрипты на пять групп по пять скриптов в каждой. Пусть наши группы называются А, Б, В, Г и Д. Скрипты тоже назовём условно: А1, А2, А3, А4 и А5 в первой группе, Б1, Б2, Б3, Б4 и Б5 — во второй и так далее.

Запустим по очереди каждую группу скриптов на наших пяти компьютерах. Запишем, в каком порядке скрипты в каждой группе завершили работу. Представим, что у нас получились такие результаты — от самого медленного до самого быстрого скрипта:

• Группа А: А3, А1, А2, А4, А5.
• Группа Б: Б4, Б3, Б5, Б1, Б2.
• Группа В: В2, В5, В4, В3, В1.
• Группа Г: Г5, Г2, Г1, Г3, Г4.
• Группа Д: Д1, Д4, Д5, Д2, Д3.

Теперь у нас есть пять скриптов-лидеров. Запустим их — это будет уже шестой раз, когда мы производим запуск. Скрипт, который завершит работу раньше остальных, — это самый быстрый скрипт из 25, что у нас есть. Он быстрее в своей группе и быстрее лидеров других групп. Представим, что первым был скрипт с названием Д3, вторым — А5, третьим — Б2, четвёртым — В1, а пятым — Г4.

Теперь сформируем наши группы скриптов заново. Раз среди скриптов-лидеров первым завершил работу Д3, переименуем его в А1, следующий за ним по скорости в изначальной группе Д — в А2 и так далее. Сделаем то же самое с остальными скриптами и их изначальными группами от самого медленного до самого быстрого:

• Новая группа А: А5, А4, А3, А2, А1.
• Новая группа Б: Б5, Б4, Б3, Б2, Б1.
• Новая группа В: В5, В4, В3, В2, В1.
• Новая группа Г: Г5, Г4, Г3, Г2, Г1.
• Новая группа Д: Д5, Д4, Д3, Д2, Д1.

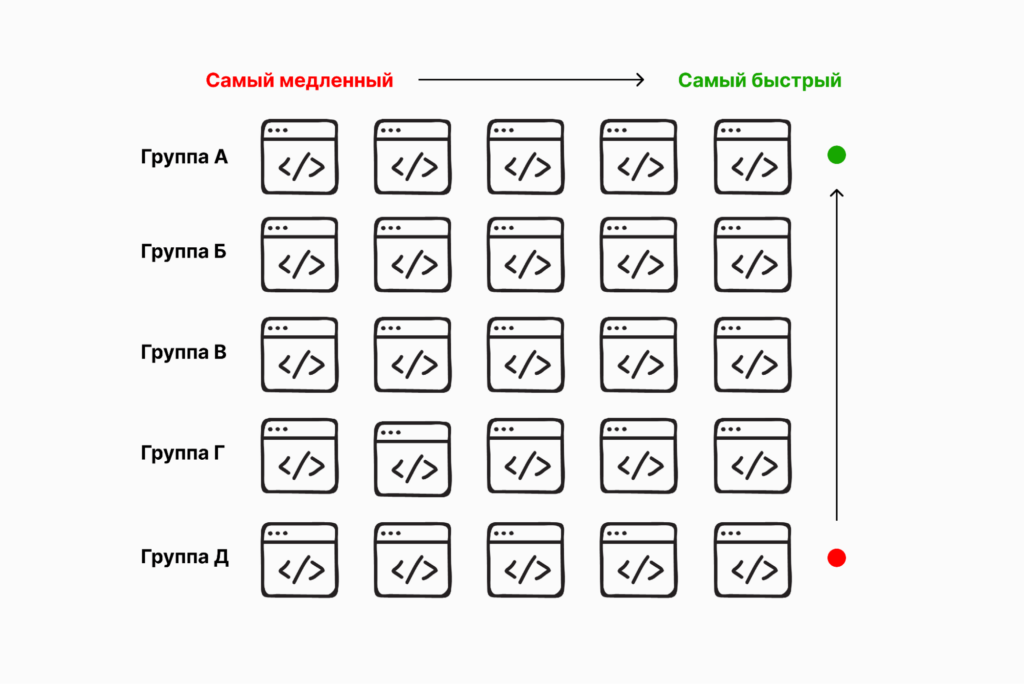
Мы знаем, какой из 25 скриптов самый быстрый, — это А1 (бывший Д3). Теперь нам нужно найти второй и третий по скорости работы. Сделать это нужно так, чтобы у нас получилось как можно меньше запусков. Для этого проанализируем наши результаты.

Поскольку лидер-скрипт из нашей новой группы Д завершил работу позже остальных лидеров из других групп, можно сделать вывод, что вся группа Д — самые медленные скрипты из 25. Это значит, что мы можем не рассматривать скрипты из этой группы:

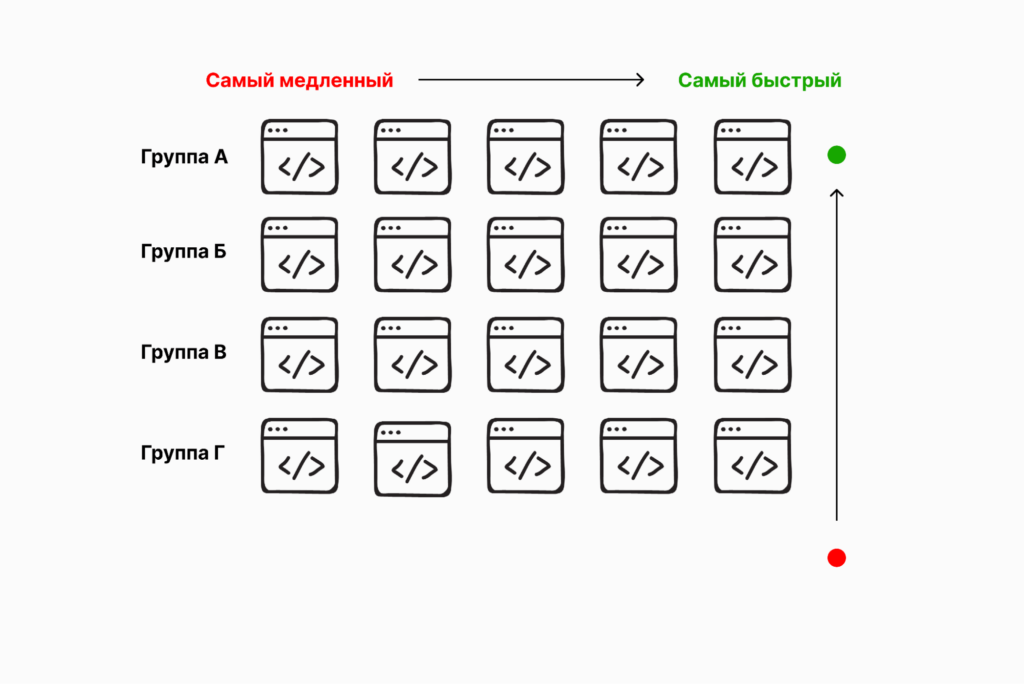
По такому же принципу мы можем сделать вывод, что все скрипты группы Г тоже медленнее, чем скрипты в группах А, Б и В. Поэтому мы можем исключить вероятность, что в группе Г могут быть второй и третий самые быстрые скрипты из 25:

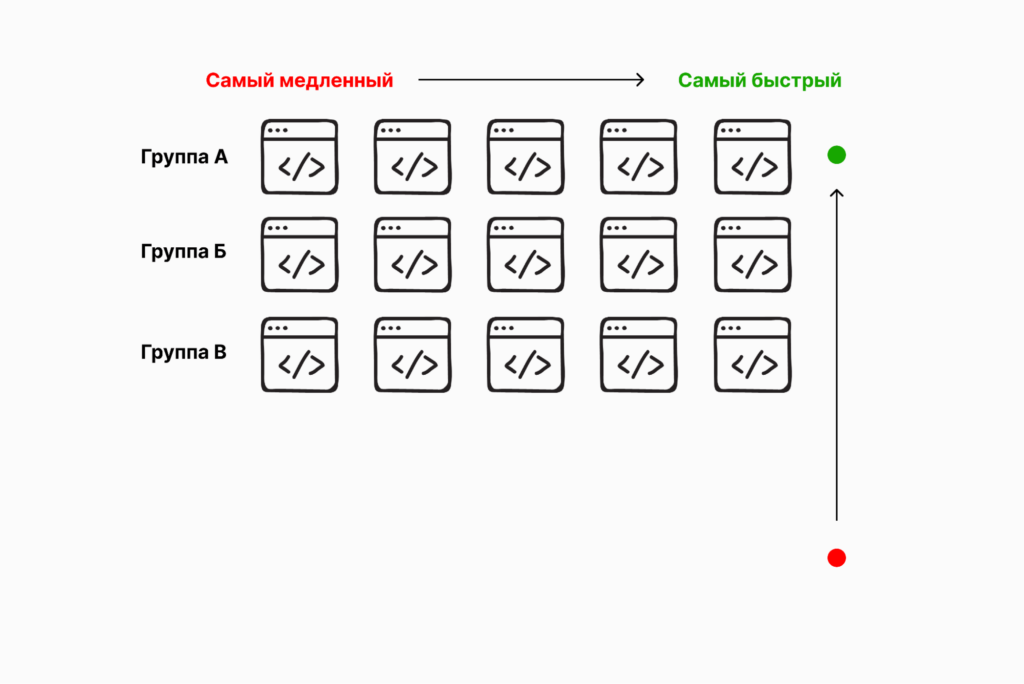
Все скрипты в группе В, за исключением В1, тоже будут медленнее, чем скрипты в группах А и Б. Их тоже исключаем из возможных кандидатов:

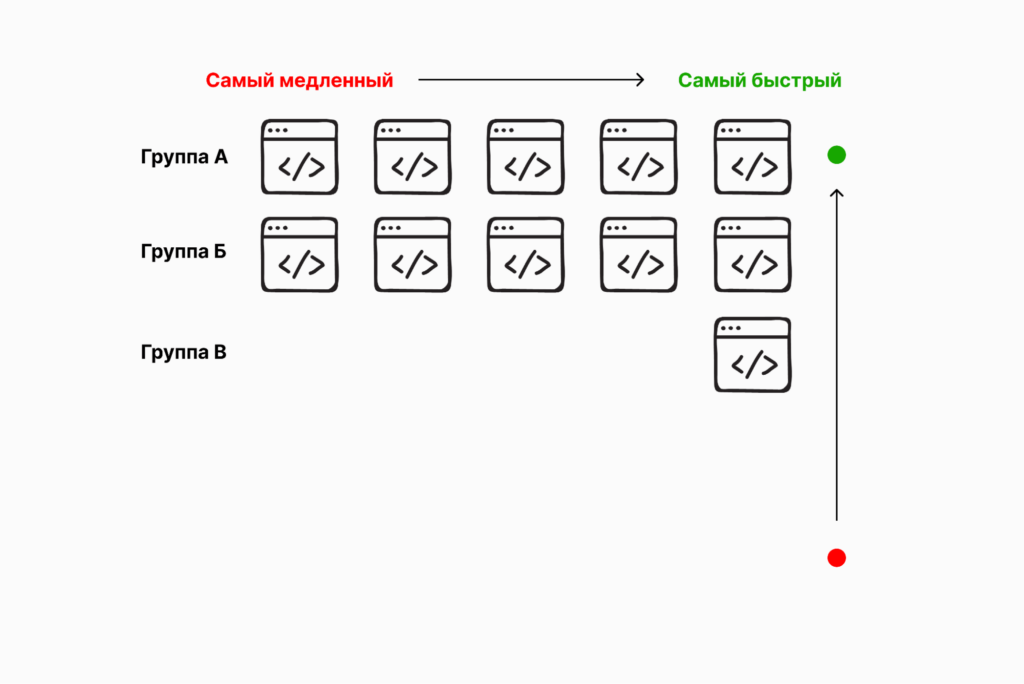
Теперь проанализируем скрипты из группы Б. Мы явно можем не рассматривать скрипты Б5, Б4 и Б3 — они медленнее, чем Б2 и Б1:

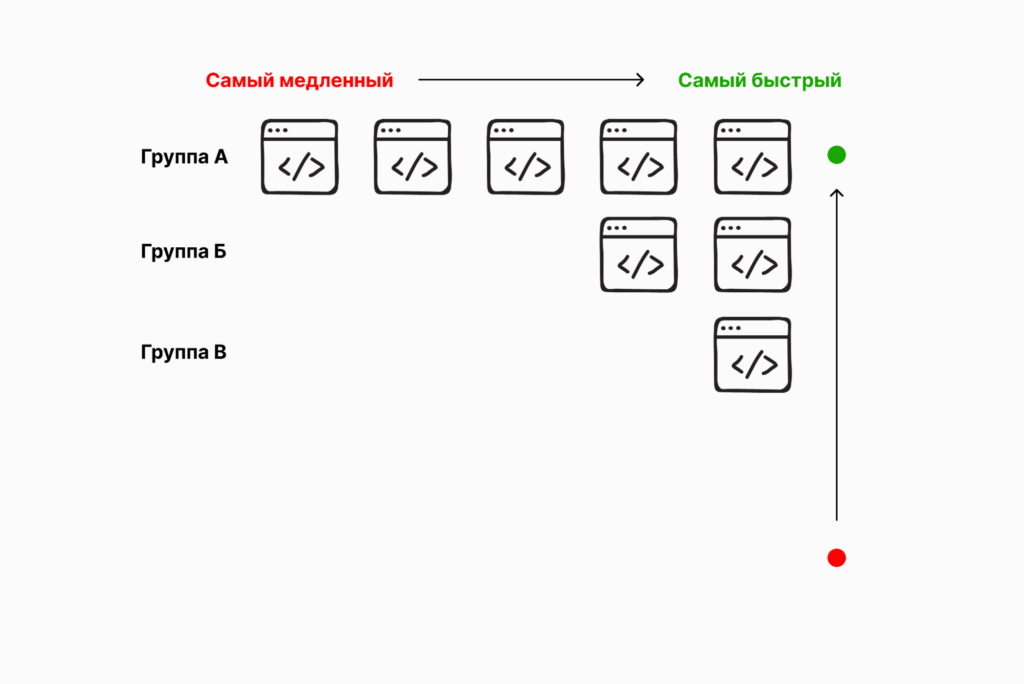
Осталось проанализировать группу А. Это самая быстрая группа скриптов, но мы точно можем исключить из дальнейшего сравнения скрипты А5 и А4:

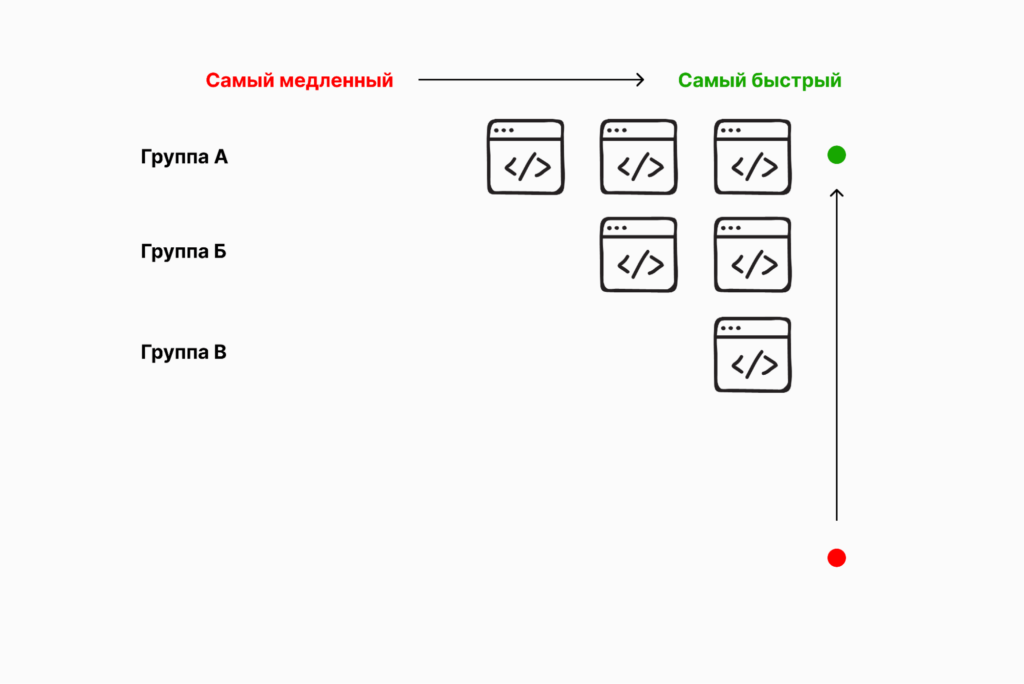
Таким образом, у нас осталось шесть скриптов, из которых нам нужно определить второй и третий по скорости работы. Но мы можем исключить из этой шестёрки скрипт А1 — мы уже точно знаем, что он самый быстрый. Это значит, что у нас осталось пять скриптов, среди которых будут такие, которые завершили бы работу вслед за А1:

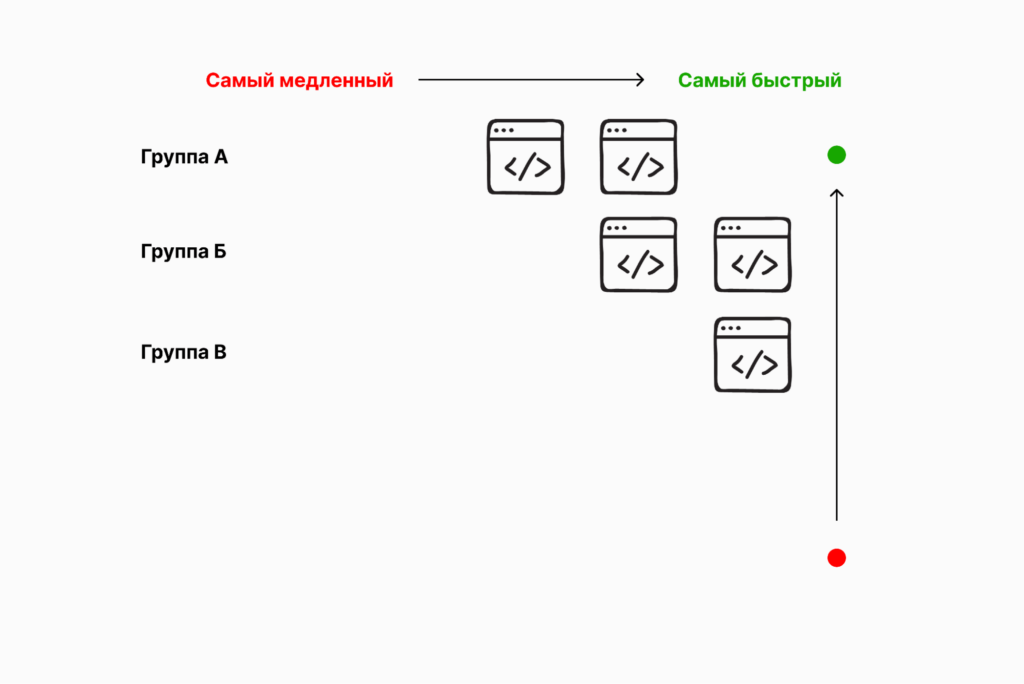
Если мы запустим скрипты А2, А3, Б1, Б2 и Г1, мы найдём второй и третий самые быстрые скрипты из 25. И это будет седьмой запуск. Получается, что минимальное количество запусков, которое нужно, чтобы найти три самых быстрых скрипта, — семь.

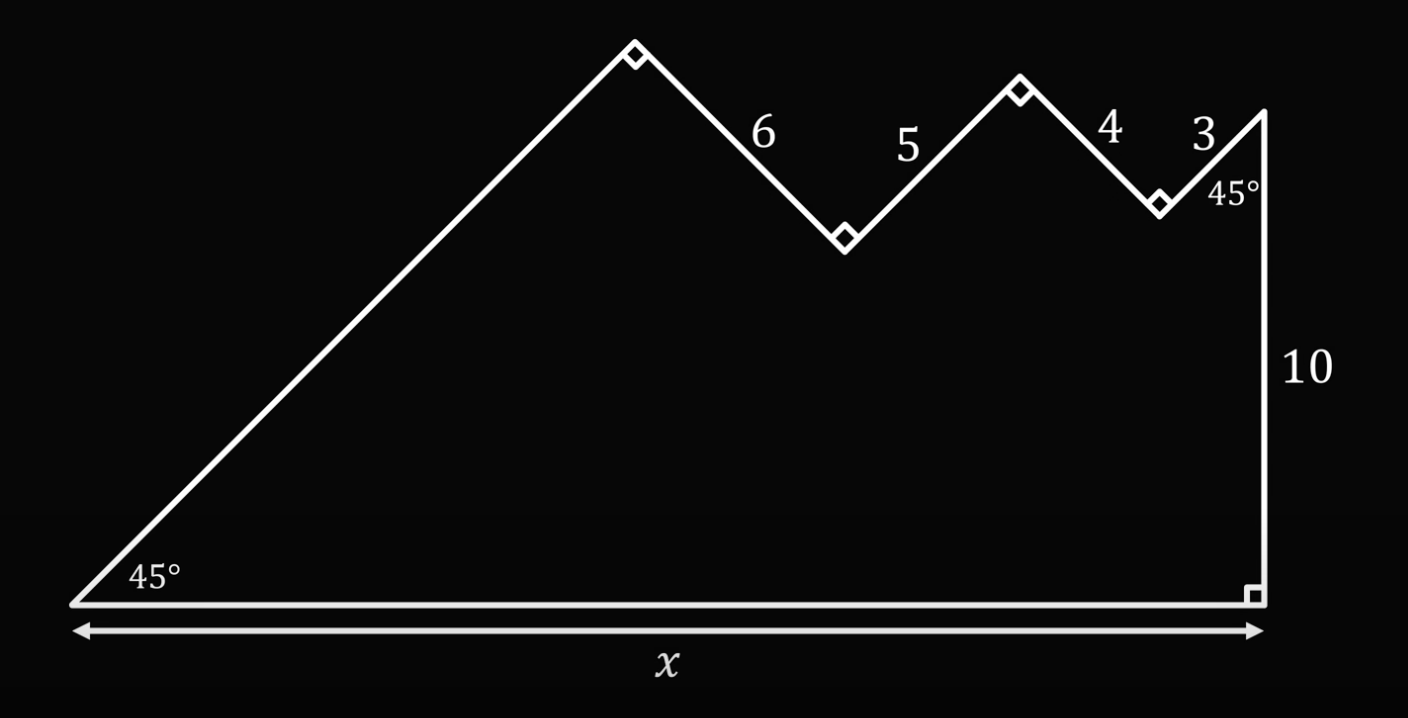
На самом деле эта задача решается довольно просто, если вспомнить школьную геометрию и свойства прямоугольных треугольников. Но чтобы ими воспользоваться, немного достроим рисунок.

Продолжим отрезок с длиной 5 до пересечения с основанием фигуры:

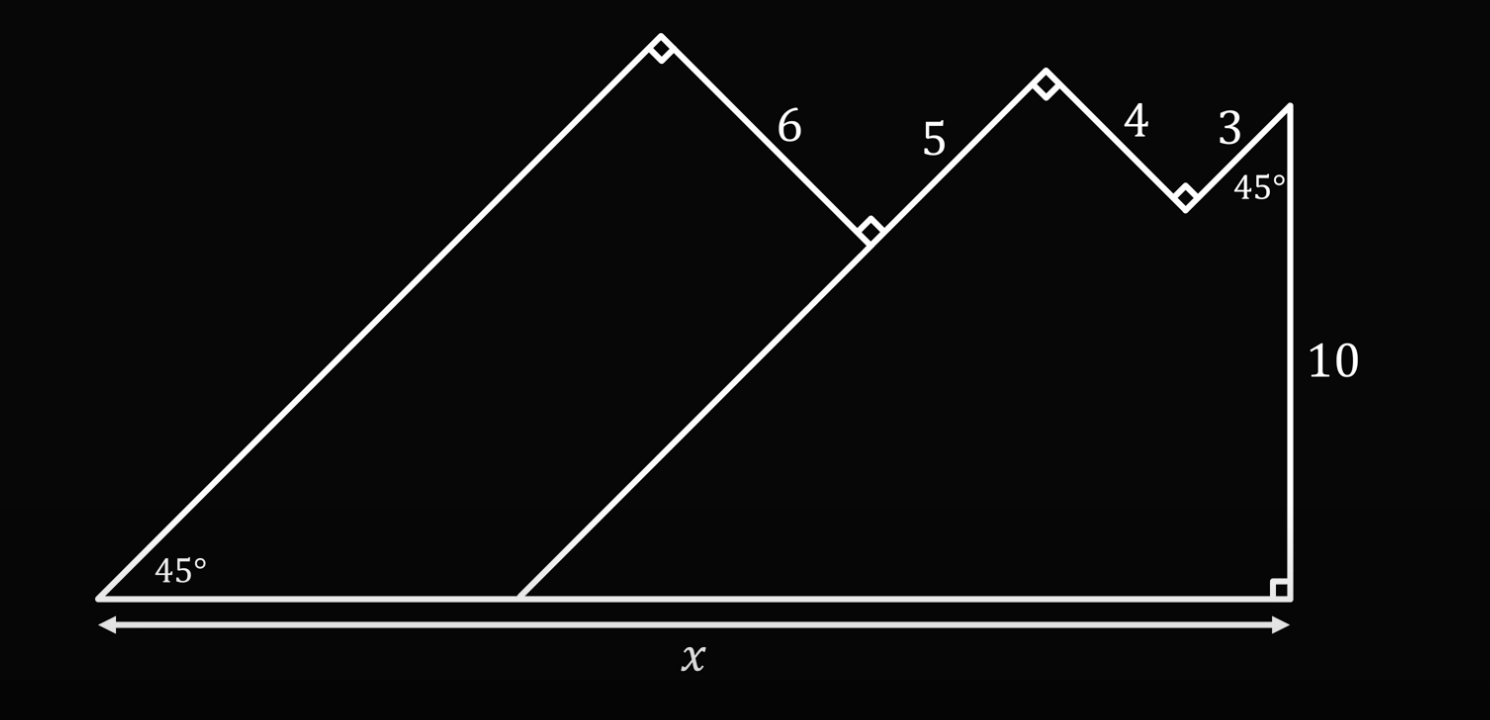
А теперь из точки пересечения проведём перпендикуляр, чтобы получить прямоугольник с короткой стороной, равной шести:

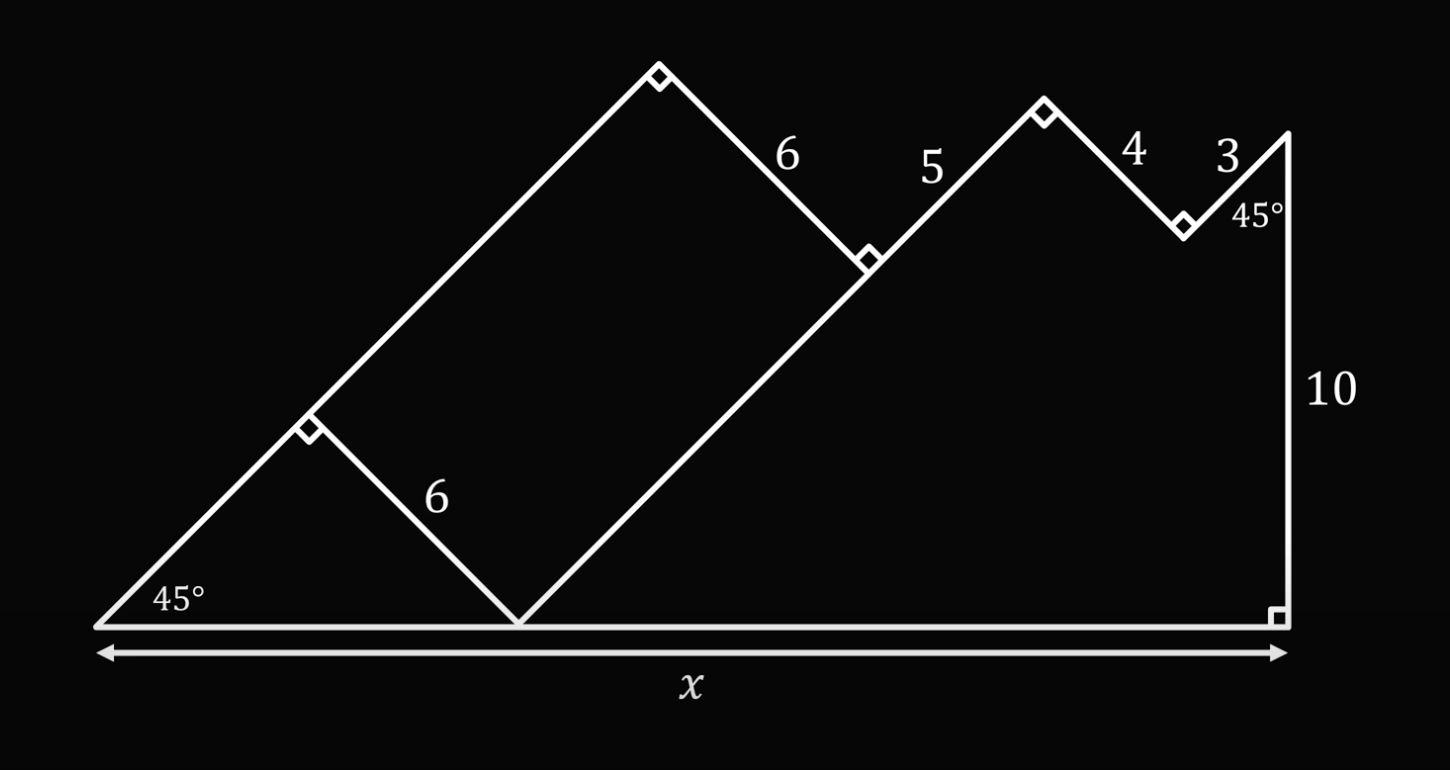
Точно так же поступим со вторым отрезком длиной 3 — продолжим его вниз до основания и проведём перпендикуляр:

Так как мы получили снова прямоугольник, где противоположные стороны равны, то и новый отрезок тоже будет равен 4:

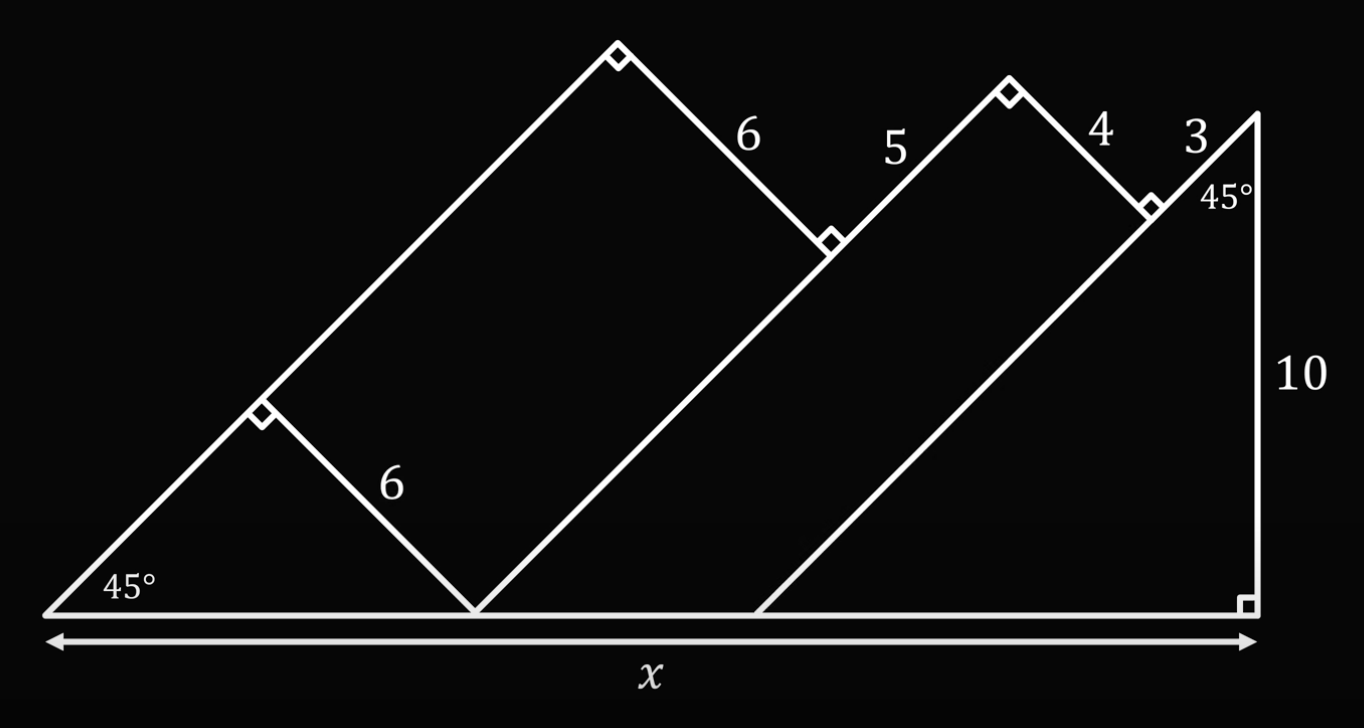
Теперь посмотрим на первый треугольник внизу, у которого одна сторона равна 6:

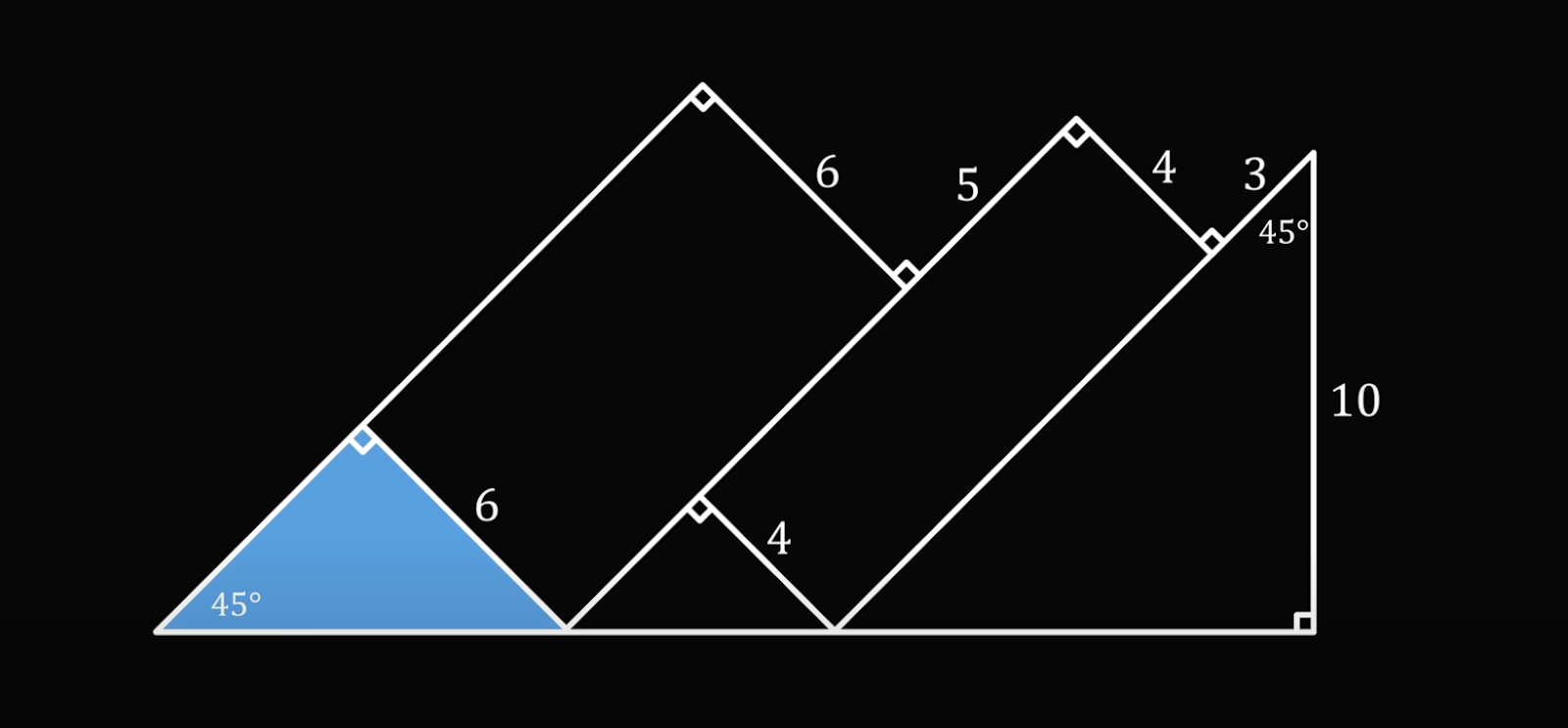
Раз один угол равен 45 градусам, а второй 90, то оставшийся угол тоже будет равен 45 (так как сумма углов в треугольнике равна 180 градусам). А раз два угла равны, то это равнобедренный прямоугольный треугольник, у которого левая сторона также равна 6.

Зная это, используем теорему Пифагора в общем виде:

x² + x² = c² → 2x² = c² → c = x√2

Здесь c — это основание нашего треугольника. Подставим вместо x шесть и получим его длину:

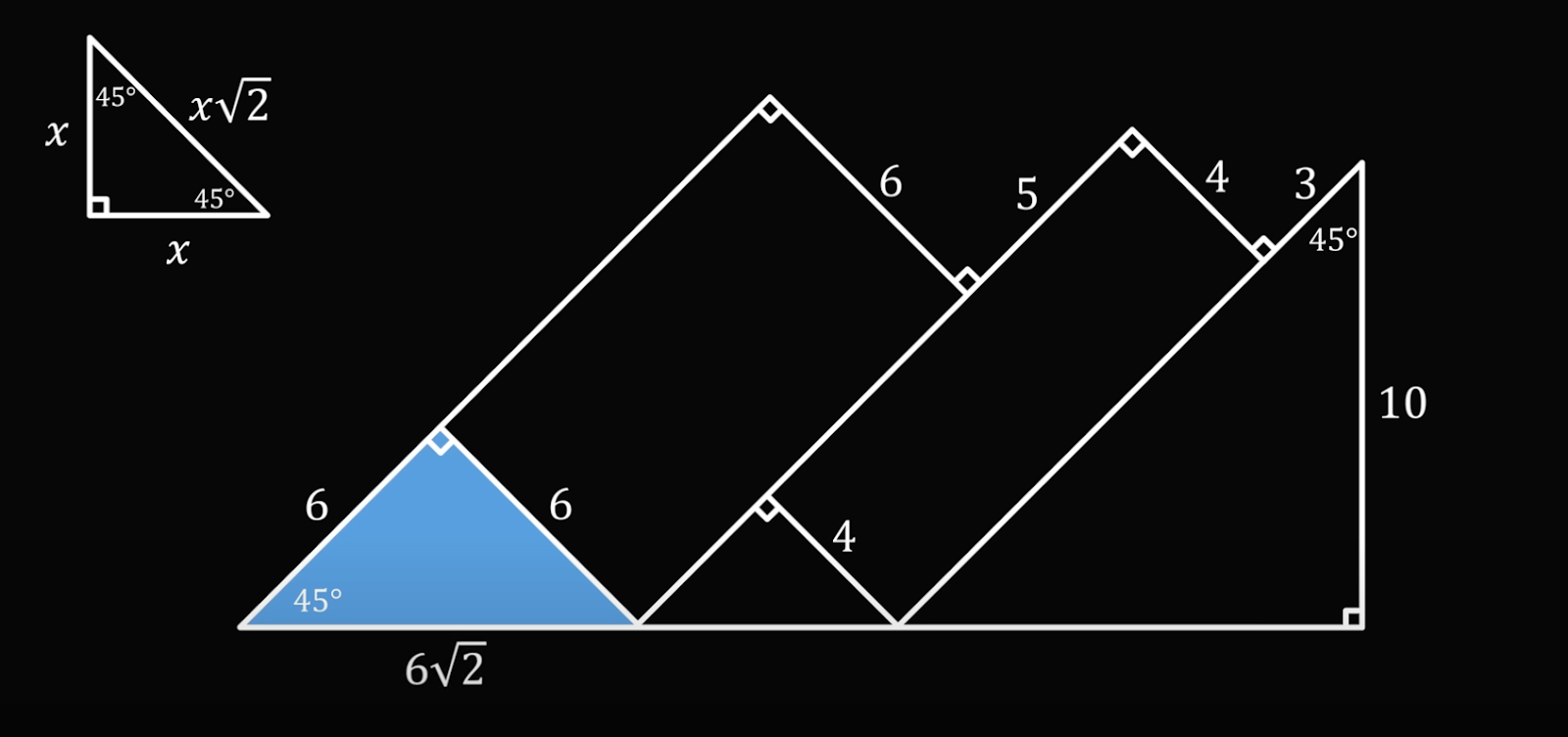
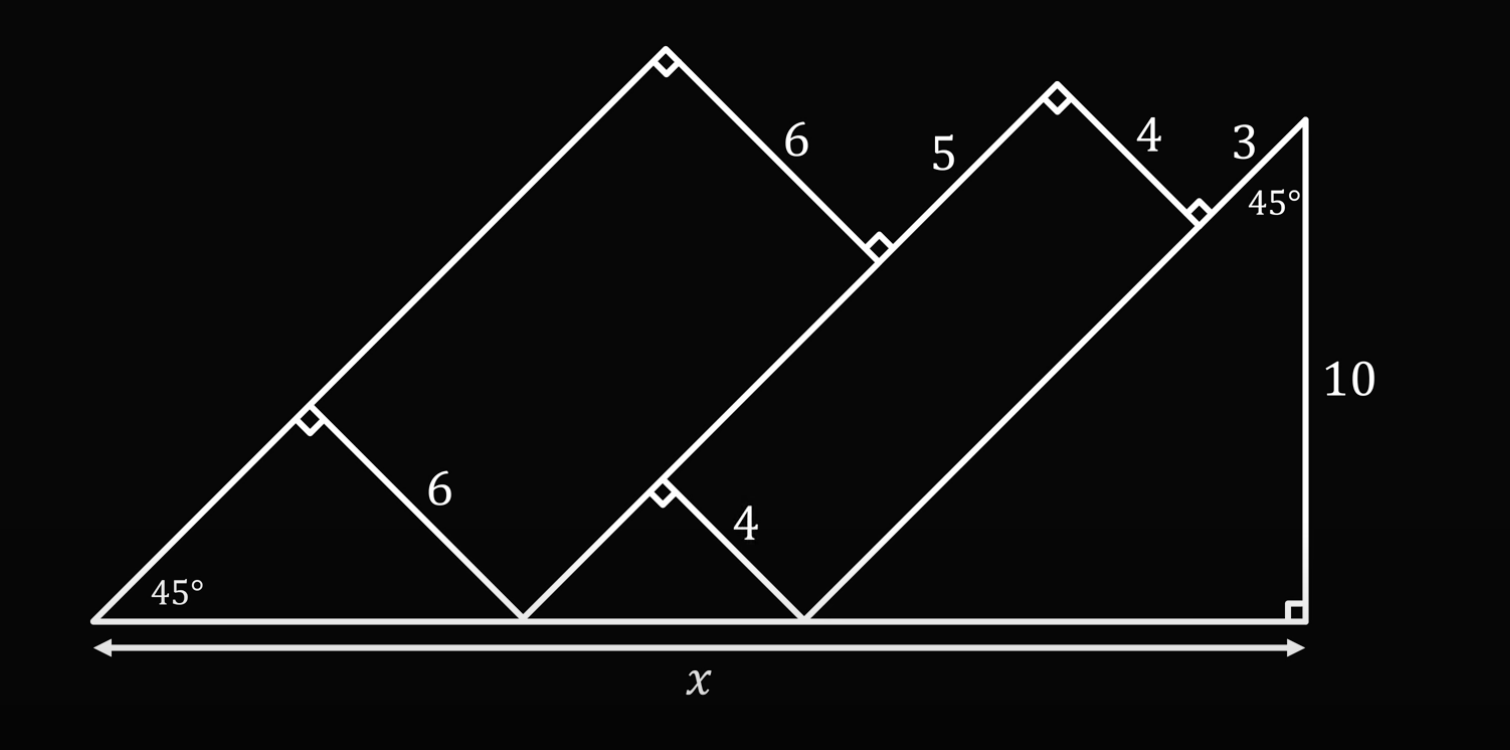
Проделаем это со вторым треугольником:

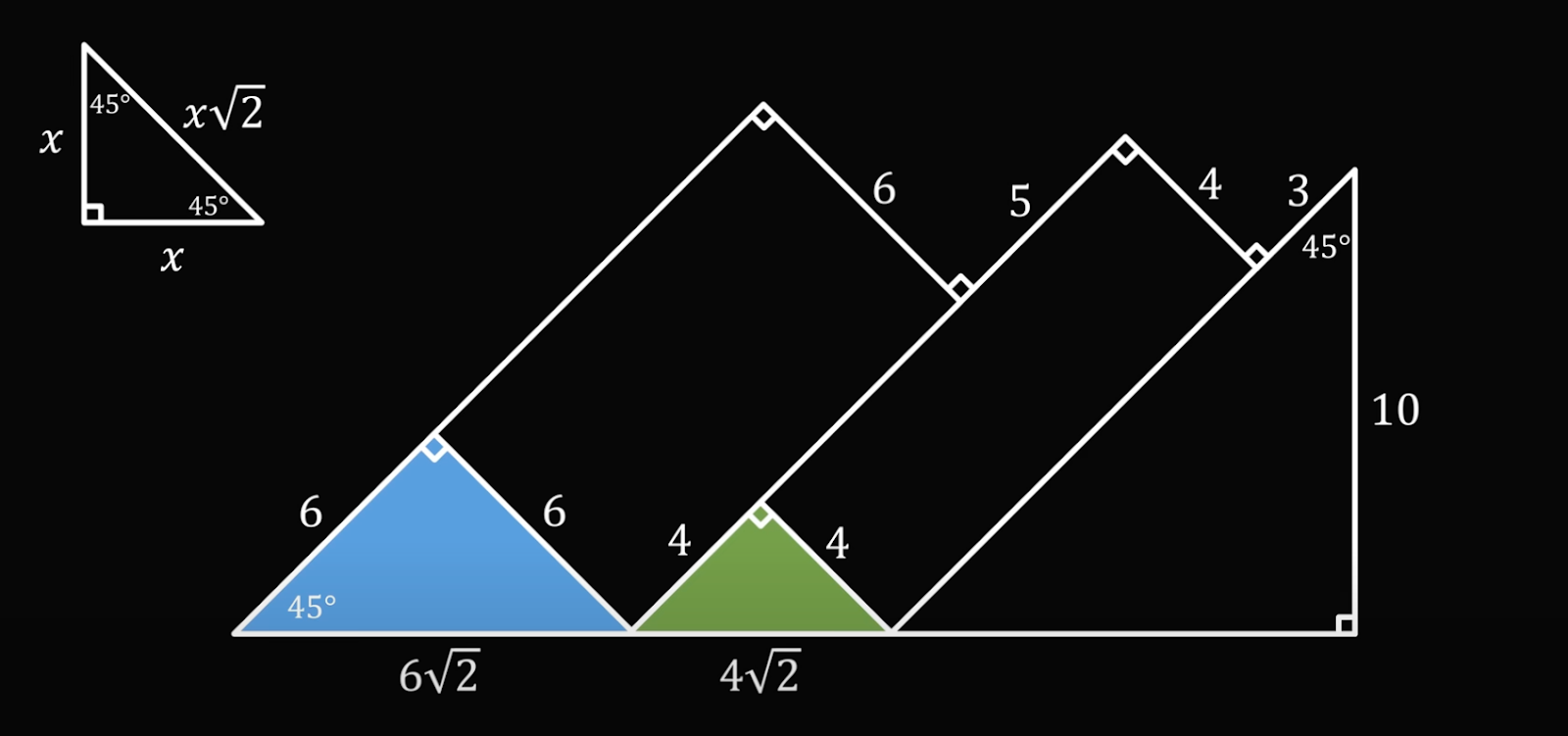
И наконец, посмотрим на третий треугольник:

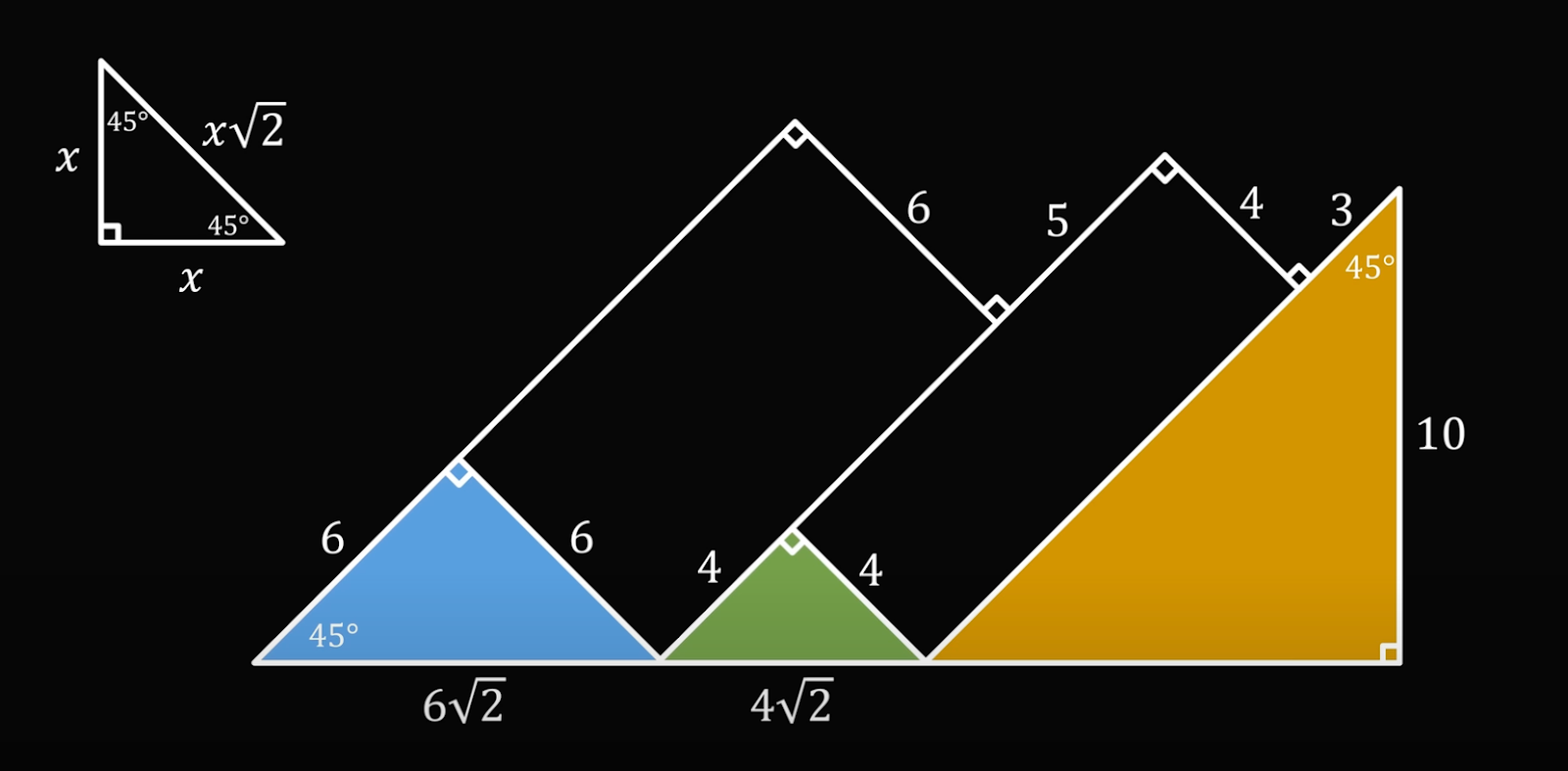
У него третий угол тоже равен 45 градусов (180 − 90 − 45 = 45), а это значит, что он тоже равнобедренный. Получается, что нижняя часть треугольника равна его правой части:

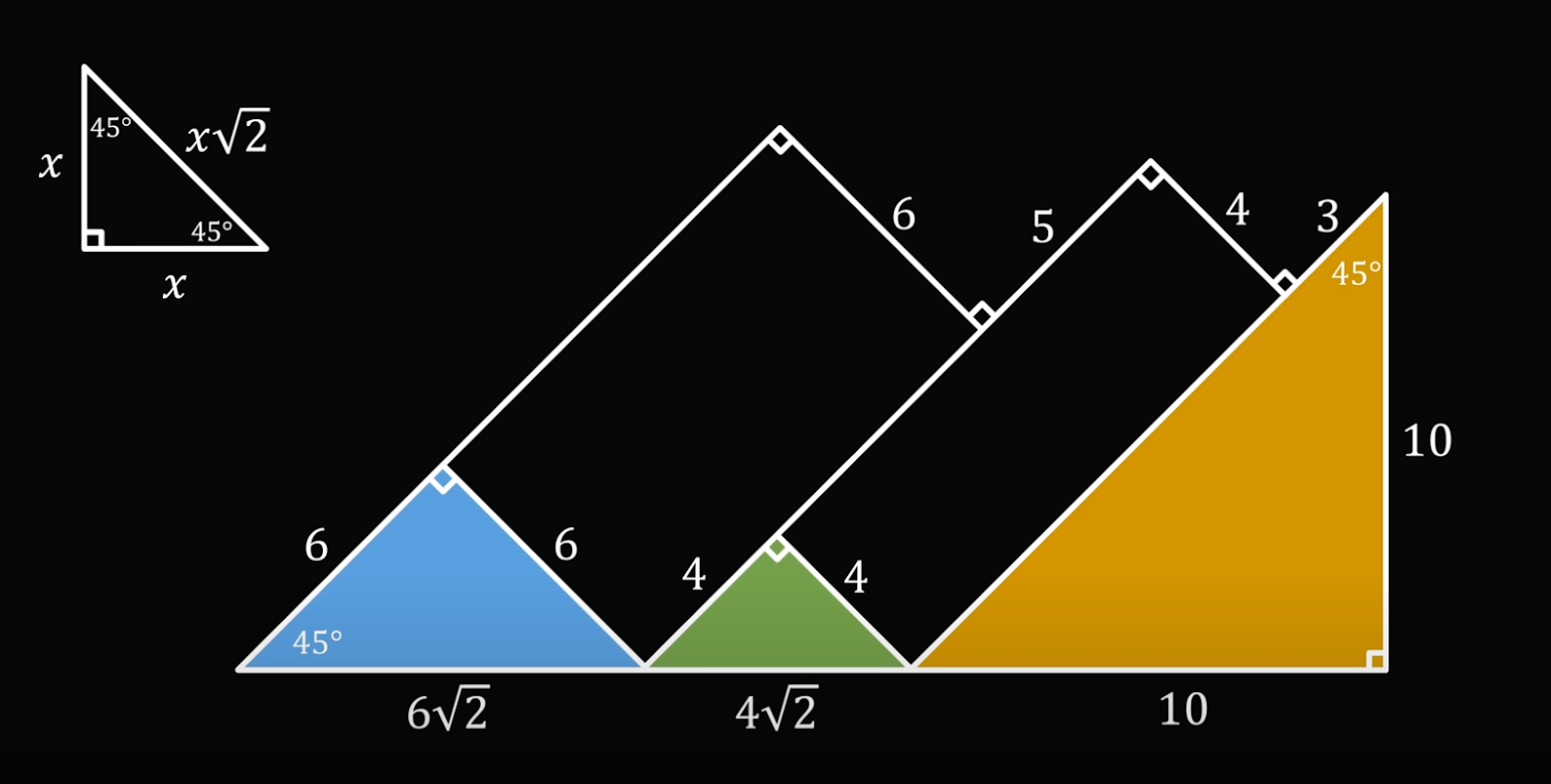
Чтобы найти общую длину основания горы, сложим все три числа:

6√2 + 4√2 + 10 = 10√2 + 10, а это примерно равно 24,14

Получается, что опытный программист был не прав, когда говорил, что не получится установить связь из-за того, что расстояние больше 25 километров.