В этой подборке задач проверяются ваши способности как аналитика. Если хотя бы половина из них вам даётся плюс-минус легко, считайте, что у вас дар системного мышления и способности к анализу. Словами классика, «Не потеряй его и не сломай».
Сложная задача про ферму, кусты и альтернативные издержки
Персонажи фильма Гая Ричи «Джентльмены» поехали на ферму собирать малину (скажем так). Малина растёт на кустах.
Когда герои приехали на место, то выяснилось, что ещё надо полить грядки, чтобы кусты продолжали расти. На всё 3 часа, а для грядок надо 100 вёдер воды.
Как героям распределить дела между собой, чтобы собрать при этом максимум ягод, если:
- Микки Пирсон (Мэтью Макконахи) за час может аккуратно собрать ягоды с 14 кустов или принести 20 вёдер воды;
- его жена Розалинда (Мишель Докери) за час может собрать ягоды с 15 кустов или принести 15 вёдер воды;
- подручный Реймонд Смит (Чарли Ханнем) за час может собрать ягоды с 25 кустов или принести 5 вёдер воды;
- Тренер (Колин Фаррелл) за час может собрать ягоды с 16 кустов или принести 26 вёдер воды. Также он может приструнить подростков и собрать их в спортзале.
Если это покажется слишком лёгким, то вот вторая часть задачи — ягоды со скольких кустов получится собрать при оптимальном подходе?
Для решения этой задачи нам понадобятся альтернативные издержки — что каждый потеряет или получит, если выберет одно или другое действие. При этом иногда альтернативные издержки можно считать не в абсолютных, а в относительных величинах — во сколько раз эффективнее будет заниматься одним, чем другим.
Чтобы понять, кто эффективнее собирает кусты малины, построим таблицу с альтернативными издержками кустов относительно воды. Это значит, что мы посчитаем, во сколько раз кому выгоднее собирать ягоды, чем носить воду. Числа в таблице — сколько сможет сделать каждый за час:
| Куст малины | Ведро воды | Альтернативные издержки на 1 куст | Рейтинг эффективности | |
| Макконахи | 14 | 20 | 20 / 14 = 1,42 | |
| Мишель | 15 | 15 | 15 / 15 = 1 | |
| Ханнем | 25 | 5 | 5 / 25 = 0,2 | |
| Фаррелл | 16 | 26 | 26 / 16 = 1,62 |
По результатам видно, что Макконахи в 1,42 раза сложнее собирать ягоды, чем носить воду, а его подручному Ханнему — в 5 раз проще собирать ягоды, чем заниматься водой. Расставим места по эффективности сбора малины — чем меньше число альтернативных издержек, тем лучше этот человек собирает малину:
| Куст малины | Ведро воды | Альтернативные издержки на 1 куст малины | Рейтинг эффективности | |
| Ханнем | 25 | 5 | 5 / 25 = 0,2 | 1 |
| Мишель | 15 | 15 | 15 / 15 = 1 | 2 |
| Макконахи | 14 | 20 | 20 / 14 = 1,42 | 3 |
| Фаррелл | 16 | 26 | 26 / 16 = 1,62 | 4 |
Теперь сделаем то же самое с водой — построим таблицу альтернативных издержек, чтобы посмотреть, кому выгоднее таскать воду, чем собирать кусты малины:
| Куст малины | Ведро воды | Альтернативные издержки на 1 куст малины | Рейтинг эффективности | |
| Фаррелл | 16 | 26 | 16 / 26 = 0,61 | 1 |
| Макконахи | 14 | 20 | 14 / 20 = 0,7 | 2 |
| Мишель | 15 | 15 | 15 / 15 = 1 | 3 |
| Ханнем | 25 | 5 | 25 / 5 = 5 | 4 |
А теперь используем показатели эффективности, основанные на альтернативных издержках, чтобы грамотно распределить задачи. Так как первостепенная задача для героев — это наносить 100 вёдер воды, то нам нужны те, кто эффективнее всего носит воду. Судя по цифрам в таблице, меньше всего альтернативных издержек по воде у Тренера (Колин Фаррелл), а на втором месте — Мэтью Макконахи. Поэтому делаем так:
- Тренер Колин Фаррелл все 3 часа носит воду и не отвлекается ни на что другое. Так за 3 часа он принесёт 78 вёдер воды.
- Макконахи тоже стартует с воды, потому что он второй по эффективности. Но ему нужно принести всего 100 − 78 = 22 ведра — остальное принесёт Тренер. После того как он принесёт эти 22 ведра, он тут же переключается на сбор малины.
- Мишель Докери, которая играет жену Макконахи, вместе с подручным Ханнемом с самого начала собирают ягоды и вообще не носят воду — так они смогут собрать больше всего.
Считаем кусты малины
- Мишель за 3 часа соберёт ягоды с 45 кустов, а Ханнем — с 75, потому что они занимаются только малиной.
- Макконахи за 3 часа мог бы собрать ягоды с 42 кустов, но у него альтернативные издержки с коэффициентом 0,7, которые он потратит на 40 вёдер воды, поэтому всего Макконахи сможет собрать ягоды с 42 − (0,7 × 22) = 26,6 куста. Пусть будет 26, чтобы не гробить целый куст. Пусть растёт до следующего раза.
- А Тренер Колин Фаррелл не соберёт ни одной ягодки, потому что всё время носит воду.
Получается, что всего за 3 часа герои соберут ягоды с 45 + 75 + 26,6 = 146 кустов.
Макроэкономическая задача про кино
Один NFT-трейдер узнал, что завтра в кино будет проходить пиратская премьера нового фильма, в связи с чем билеты будут дешевле, чем обычно. Обычно билет стоит 500 рублей, а завтра — 400. С одной стороны, это выгодный поход в кино, а с другой — он хотел завтра остаться дома и поботать матешу перед ЕГЭ.
Так как это был очень прагматичный трейдер, он решил посчитать альтернативные издержки в каждом случае и принять экономически верное решение. Но в итоге он запутался в расчётах, так и не выяснив, какую выгоду он упускает в каждом случае. Помогите ему посчитать издержки и построить планы на завтрашний день:
👉 Что выгоднее — остаться завтра дома или пойти в кино со скидкой?
Кажется, что, оставшись дома, школьник-трейдер сэкономит 400 рублей, поэтому это выгодное решение. Но на самом деле всё немного не так. Посмотрим на это экономически.
Для начала нужно очертить альтернативы. Сейчас мы рассчитываем два варианта поведения: пойти в кино завтра и пойти не завтра, но не позднее, чем будет ЕГЭ. Сейчас мы не рассматриваем варианты «не пойти вообще» или «скачать фильм из интернета».
Предположим, что до ЕГЭ осталось 20 дней
Для начала убедимся, что эти варианты равнозначны во всём, кроме денег:
Если пойдём завтра:
✅ Посмотрим фильм.
✅ К экзамену поботаем в любой день, кроме завтра (то есть 19 дней).
✅ Потратим 400 рублей.
Если пойдём в другой день:
✅ Посмотрим фильм.
✅ К экзамену поботаем в любой день, кроме дня похода в кино (то есть 19 дней).
✅ Потратим 500 рублей.
Уже на этом этапе очевидно, что первый вариант на 100 рублей выгоднее. Но давайте убедимся в этом с помощью экономики.
Ценность пойти завтра на премьеру равна −400 рублей (потому что мы их тратим). Остаться дома и пойти в другой день в кино будет стоить −500 рублей. Вычитаем из выгоды второго случая ценность первого случая, чтобы получить общую стоимость альтернативных издержек: −500 −(−400) = 400−500 = −100 рублей.
А вот что будет, если не изолировать варианты выбора:
- Не смотрим фильм вообще, не получаем эмоции и т. д.
- Готовимся к экзамену 20 дней.
- Тратим ноль рублей.
- Смотрим фильм в кино после ЕГЭ.
- Готовимся к экзамену 20 дней.
- Тратим 500 рублей.
- Смотрим фильм в интернете после ЕГЭ.
- Готовимся к экзамену 20 дней.
- Тратим 0 рублей.
- Дождаться, когда кто-то из одноклассников позовёт на ДР в кино после ЕГЭ.
- Посмотреть фильм с одноклассником.
- Готовиться к экзамену 20 дней.
- Тратить 0 рублей на фильм, но сколько-то — на подарок.
Чем больше переменных мы вводим в это сравнение, тем сложнее оценить экономическую выгоду от какого-то решения. Например, мы решили посмотреть фильм в кино после ЕГЭ. С одной стороны, мы выигрываем один день подготовки и он нам стоит 100 рублей в альтернативных издержках. Но что, если через 20 дней фильм уже не будет идти? Или цены на билеты изменятся? Одно это изменение делает сравнение почти нереальным.
И чем дальше — тем хуже. Если сравнивать кинотеатр сегодня и торренты через 25 дней — это сравнивать несравнимые вещи.
Поэтому это не упражнение на вычитание 400 из 500. Это упражнение на изолирование вариантов выбора.
Задача про выгодную торговлю между странами
Вилларибо и Виллабаджо решили наладить выгодный товарообмен и начали с двух товаров — сыра и вина. Сыр и вино есть в обеих странах.
Предприятие в Вилларибо в среднем может за 20 часов сделать тонну сыра, а у Виллабаджо на это уходит 40 часов. Зато комбинат в Виллабаджо может за 25 часов сделать тонну вина, на что в Вилларибо понадобится целых 100 часов.
Страны хотят меняться товарами в соотношении 1:3 — одна страна отдаёт тонну одного товара и получает 3 тонны другого. Кому и чем выгодно меняться в этом случае?
Задание со звёздочкой: а как вообще странам найти диапазон взаимовыгодной торговли?
Чтобы каждой стране понять, чем ей выгоднее торговать, ей нужно знать альтернативные издержки каждого товара. У какого товара будут самые маленькие альтернативные издержки — такой и станет самым выгодным в производстве.
Нам нужно перейти от затрат в часах к количеству тонн, которые каждая страна сделает за час. Для этого разделим единицу (одну тонну) на количество часов:
| Количество тонн в час | Вилларибо | Виллабаджо |
| Сыр | 1/20 | 1/40 |
| Вино | 1/100 | 1/25 |
Теперь мы можем посчитать альтернативные издержки по сыру и вину для каждой страны. Например, чтобы найти альтернативные издержки для сыра в Вилларибо, разделим 1/100 (столько тонн вина можно сделать за час) на 1/20 и получим 20/100. Аналогично сделаем остальное:
| Количество тонн в час | Вилларибо | Альтернативные издержки | Виллабаджо | Альтернативные издержки |
| Сыр | 1/20 | 20/100 = 0,2 | 1/40 | 40/25 = 1,6 |
| Вино | 1/100 | 100/20 = 5 | 1/25 | 25/40 = 0,625 |
Получается, что в Вилларибо самые низкие альтернативные издержки у сыра, а у Виллабаджо — у вина, поэтому этим странам выгоднее всего производить эти продукты.
Теперь найдём, кому что выгоднее менять в соотношении 1 к 3.
Вариант: сыр Вилларибо на вино Виллабаджо. Если Вилларибо будет продавать 1 тонну сыра, то покупать будет 3 тонны вина. Это значит, что для производства 1 тонны сыра Вилларибо потратит 20 часов. Но если бы она захотела сделать 3 тонны вина самостоятельно, ей бы понадобилось 100 × 3 = 300 часов. Значит, выгода от такого обмена для Вилларибо — 300 − 20 = 280 часов.
Теперь посмотрим на ситуацию глазами Виллабаджо. Ей нужно отдать 3 тонны вина, на которые она потратит 25 × 3 = 75 часов. В ответ она получит тонну сыра, которую сама смогла бы сделать за 40 часов, а значит, выгода от такого обмена для Виллабаджо составляет 40 − 75 = −35 часов. Получается, что так меняться ей невыгодно — она потратит времени больше, чем сэкономит.
Итого при таком обмене:
✅ Вилларибо получает выгоду 280 часов.
❌ Виллабаджо получает выгоду −35 часов.
Вывод: такая схема выгодна только Вилларибо.
Вариант: сыр Виллабаджо на вино Вилларибо. Зайдём с другой стороны — пусть Виллабаджо меняет 1 тонну вина на 3 тонны сыра. Для производства тонны вина Виллабаджо потребуется 25 часов, а на 3 тонны сыра — 40 × 3 = 120 часов. Выгода от такого обмена составит 120 − 25 = 95 часов.
При этой же схеме Вилларибо на производство 3 тонн сыра понадобится 20 × 3 = 60 часов, а на тонну самостоятельно изготовленного вина — 100 часов. Выгода от такого обмена составит 100 − 60 = 40 часов.
Итого при таком обмене:
✅ Вилларибо получает выгоду 40 часов.
✅ Виллабаджо получает выгоду 95 часов.
Вывод: такая схема выгодна обеим сторонам, хотя для Вилларибо она менее выгодна, чем предыдущая.
Диапазон выгодной торговли — ситуация, при которой обеим странам выгодно заключать торговые сделки.
Если у Вилларибо альтернативные издержки сыра составляют 0,2, то это значит, что вместо одной тонны сыра она сможет производить 0,2 тонны вина. Получается, что Вилларибо будет с удовольствием менять свой сыр на вино, когда она за тонну сыра сможет получить больше, чем 0,2 тонны вина.
У Виллабаджо альтернативные издержки сыра составляют 1,6 — это значит, что она легко купит сыр, когда отдаст за него меньше, чем 1,6 тонны вина. Ей будет выгодно отдать меньше вина за тонну сыра, то есть сэкономив время, которое ей самой нужно на производство того же объёма сыра.
Получается, что тонна сыра из Вилларибо меняется на диапазон от 0,2 до 1,6 тонны вина из Виллабаджо — и это будет выгодно обеим странам.
Если посмотреть на таблицу, то становится очевидно, что диапазон выгодной торговли зависит от альтернативных издержек аналогичных товаров:
| Альтернативные издержки | Вилларибо | Виллабаджо | На что меняем |
| Сыр | 0,2 | 1,6 | Вино |
| Вино | 5 | 0,625 | Сыр |
Это значит, что диапазон выгодной торговли одной тонны вина из Виллабаджо меняется на диапазон от 0,625 до 5 тонн сыра из Вилларибо — и это тоже будет выгодно обеим странам. А в первом решении у нас как раз за 1 тонну вина дают 3 тонны сыра — и это выгодно, потому что укладывается в диапазон выгодной торговли.
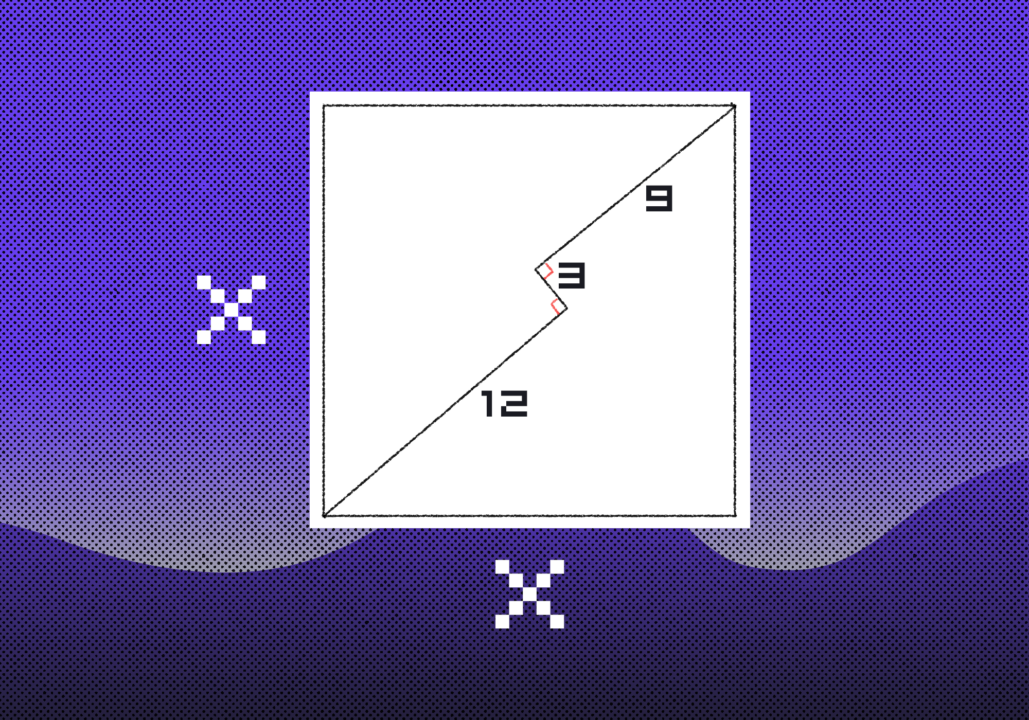
Сложная задача про игральные кубики и вероятности
Вот логическая задачка на вероятности. Есть четыре шестигранных кубика, на каждом нанесены числа в такой комбинации:
на одном стоят числа 3, 3, 3, 3, 3, 3 (получается, на каждой стороне по тройке);
на втором — 0, 0, 4, 4, 4, 4 (две стороны с нулями, на остальных по четвёрке);
на третьем — 1, 1, 1, 5, 5, 5 (три стороны с единицами, три с пятёрками);
на четвёртом — 2, 2, 2, 2, 6, 6 (четыре с двойками, две с шестёрками).
Есть два игрока. Каждый выбирает кубик на всю игру. В каждом раунде участники кидают кубик и смотрят, у кого больше.
Всего в игре тысяча раундов. У кого больше побед за всю игру — тот и выиграл. Вы можете выбрать кубик первым. Какой кубик нужно выбрать, чтобы с наибольшей вероятностью выбрать?
Раз игроки бросают кубик не один, а тысячу раз подряд, то победит тот, у кого будет выше вероятность получить за один бросок больше очков, чем у соперника. Вероятность — это насколько возможно, что произойдёт то, что нам нужно. Например, в обычном кубике 6 разных чисел, поэтому вероятность выпадения любого числа — ⅙.
Чтобы решить эту задачу, посчитаем вероятности выигрыша или проигрыша при выборе каждого из четырёх кубиков.
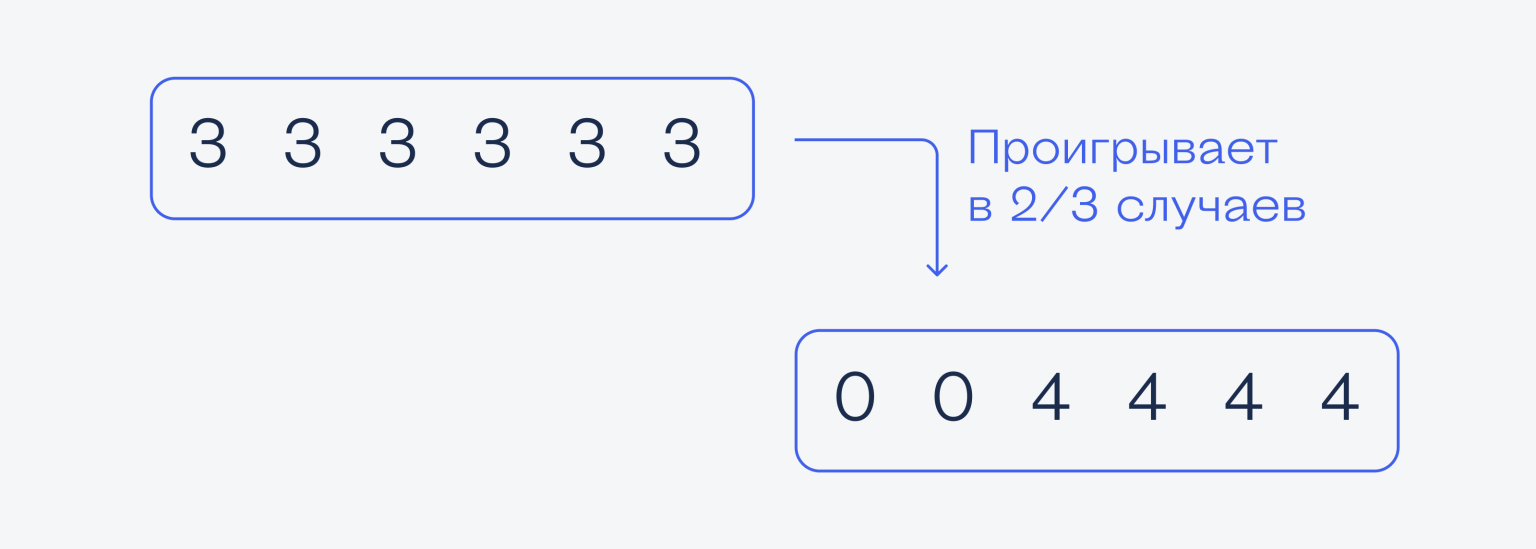
Тройки. Допустим, мы выбрали кубик с тройками, а соперник — кубик с четвёрками. Если у него выпадет 0, то он проиграет, потому что у нас всегда выпадает 3. Ноль у него выпадет 2 раза из 6, поэтому у него вероятность проиграть равна 2/6, или ⅓. При этом если у него выпадет 4, то он выиграет, а случится это 4 раза из 6 (потому что из 6 граней на 4 из них нарисована четвёрка).
Получается, что в этом случае соперник выиграет в 4/6, или ⅔ случаев. Это значит, что на дистанции в 1000 бросков мы в среднем выиграем 333 раза и проиграем 667 раз. Этот вариант не очень.
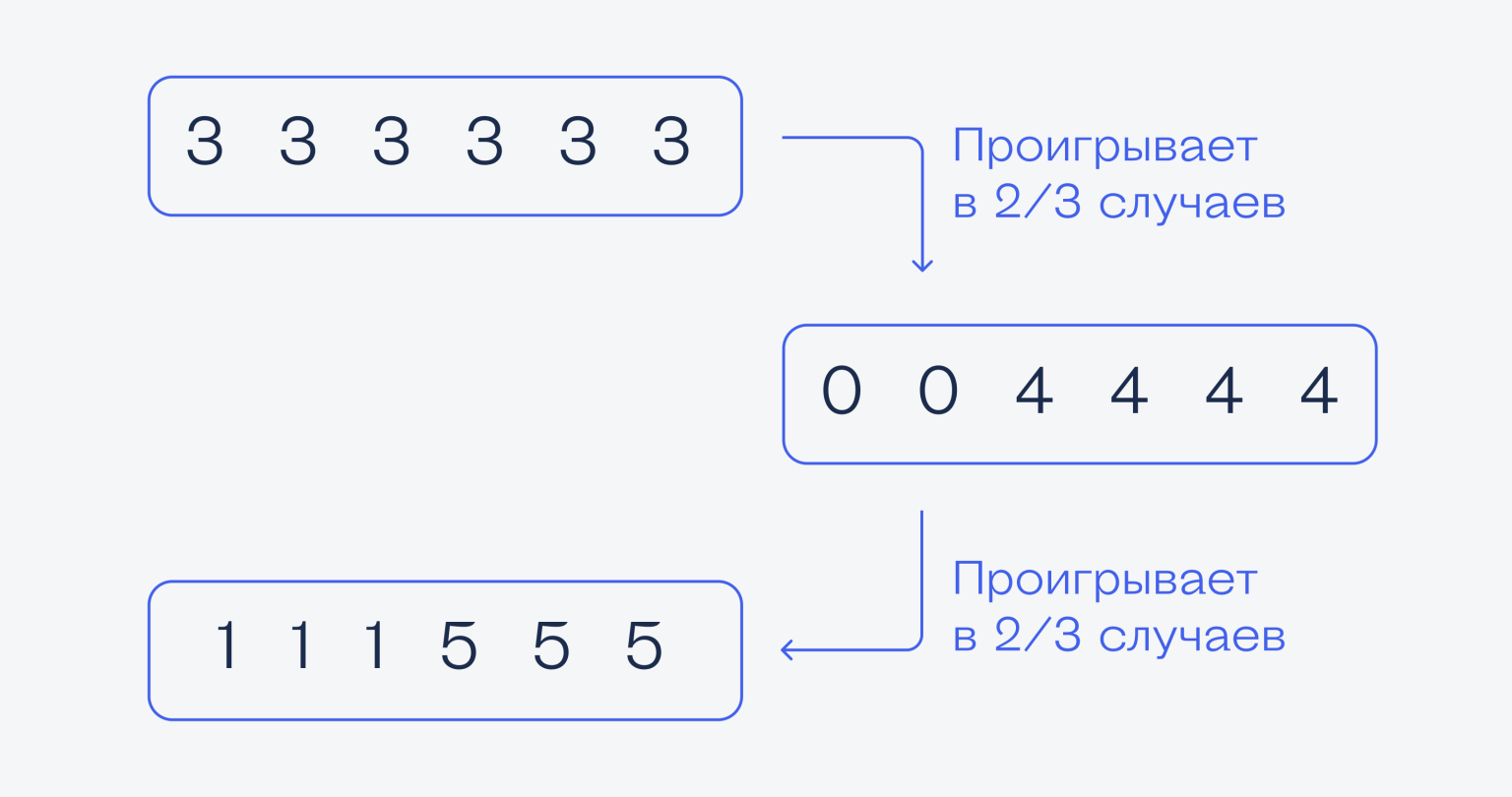
Четвёрки. Допустим, мы взяли кубик с четвёрками, а соперник — с пятёрками. В этом случае соперник точно выиграет, если у него выпадет 5 — потому что у нас только 0 и 4 (это значит, что вероятность выкинуть 0 или 4 у нас равна единице, то есть будет всегда). Пятёрка может выпасть в 3 случаях из 6, поэтому вероятность такого события равна 3/6, или ½. В остальной половине случаев, когда у него выпадает единица, мы всё равно можем проиграть, если у нас выпадет ноль. Ноль у нас выпадает 2 раза из 6, то есть с вероятностью ⅓.
Чтобы посчитать общую вероятность победы соперника, надо сложить все вероятности отдельных побед:
½ (у него выпало 5) × 1 (вероятность того, что у нас будет 0 или 4);
+
½ (у него выпало 1) × ⅓ (у нас выпал ноль);
=
½ + ⅙ = ⅔.
Получается, что если мы выберем кубик с четвёрками, а соперник — с пятёрками, то мы проиграем в ⅔ случаев. Так может, надо выбрать кубик с пятёрками?
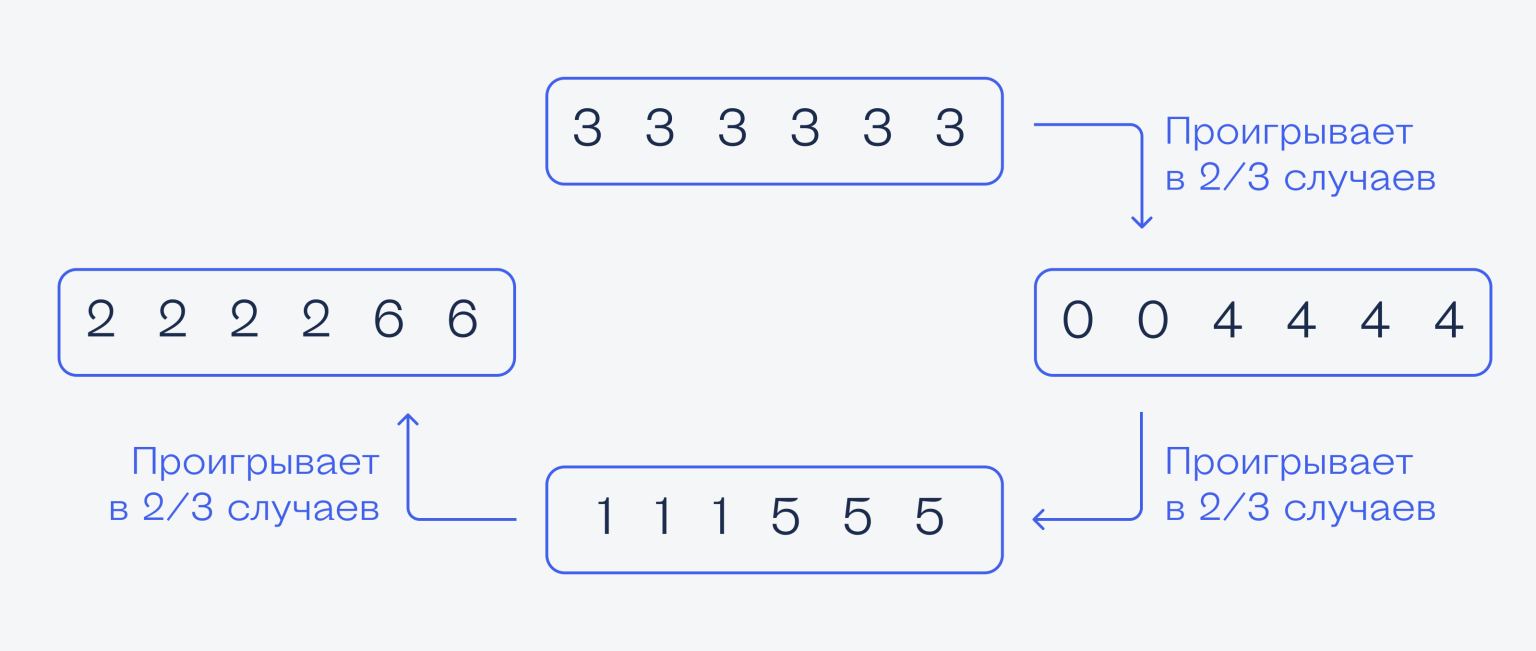
Пятёрки. Допустим, мы выбрали кубик с пятёрками, а соперник — с шестёрками. В этом случае соперник точно выиграет, если у него выпадет 6 — потому что у нас только 1 и 5 (и вероятность проигрыша при этом равна единице). Шестёрка может выпасть в 2 случаях из 6, поэтому вероятность такого события равна 2/6, или ⅓. В остальных случаях, когда у него выпадает двойка (4 раза из 6, то есть с вероятностью 4/6, или ⅔), мы всё равно можем проиграть, если у нас выпадет единица. Она у нас выпадает 3 раза из 6, то есть с вероятностью ½.
Чтобы посчитать общую вероятность победы соперника, надо сложить все вероятности отдельных побед:
⅓ (у него выпало 6) × 1 (вероятность того, что у нас будет 1 или 5);
+
⅔ (у него выпало 2) × ½ (у нас выпала единица);
=
⅓ + ⅓ = ⅔.
Получается, что если мы выберем кубик с пятёрками, а соперник — с шестёрками, то мы проиграем в ⅔ случаев. Тогда выбираем кубик с шестёрками?
Шестёрки. Допустим, мы решили брать кубик с шестёрками. В этом случае соперник выберет кубик с тройками, и вот почему.
Соперник выиграет, только если у него выпадет 3 (а это будет всегда), если у нас будет двойка — а она выпадет с вероятностью 4/6, или ⅔. Получается, что если мы выберем кубик с шестёрками, а соперник — с тройками, то мы проиграем в ⅔ случаев. Тогда что нам выбрать?
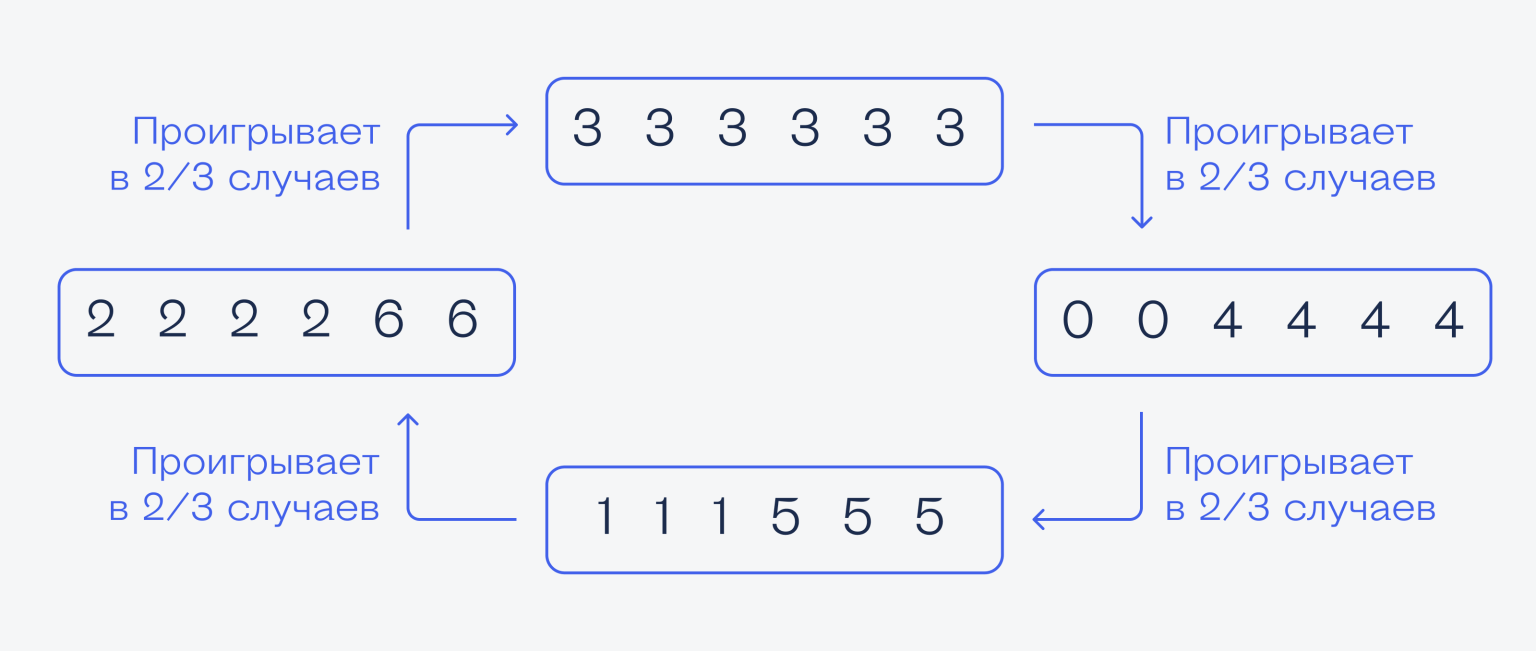
Какой вывод? Тот, кто выбирает кубик первым, всегда будет проигрывать после 1000 бросков, если соперник выберет тот кубик, который принесёт ему выигрыш в ⅔ случаев. Поэтому, какой бы кубик мы ни выбрали, если соперник не дурак, он нас обыграет.
Задача, в которой потребуется вся ваша логика
Есть два верных утверждения:
- Буратино всегда врёт.
- Буратино однажды сказал «Все мои шляпы — зелёные».
Какие выводы можно из этого точно сделать?
- у Буратино есть как минимум одна шляпа.
- у Буратино есть только одна зелёная шляпа.
- у Буратино нет шляп.
- у Буратино есть как минимум одна зелёная шляпа.
- у Буратино нет зелёных шляп.
Обратите внимание на слово «точно»: выводы должны устоять при любой логической проверке в любой ситуации. То есть наши выводы и его ложь не должны логически противоречить друг другу ни при каких мыслимых условиях.
Чтобы решить эту задачу, нам понадобится математическая логика и знакомые по программированию понятия TRUE (истина) и FALSE (ложь).
То, что Буратино всегда врёт, означает, что любая его фраза на выходе меняет своё значение на противоположное и имеет значение FALSE. А это значит, что вывод, который мы можем сделать, должен иметь значение TRUE: когда Буратино соврёт, он заменит его значение на противоположное и получит FALSE.
Получается, что нам нужно подставить все предположения по очереди в эту фразу и посмотреть, есть ли такие условия, в которых фраза Буратино станет истиной, либо мы сможем легко это опровергнуть.
У Буратино есть как минимум одна шляпа. Если фраза «Все мои шляпы — зелёные» ложная, значит, у Буратино может быть как минимум одна шляпа другого цвета:
✅ (есть как минимум одна шляпа) → (есть синяя шляпа) = TRUE
Получается, что это высказывание может быть правдой, и Буратино, соврав, скажет, что все его шляпы зелёные — то, что нам подходит. При этом мы точно знаем, что это не может быть зелёной шляпой, иначе Буратино скажет правду, а по условиям это невозможно.
Единственное, чем это можно опровергнуть — это фраза «у Буратино нет шляп». Но мы не будем опровергать это высказывание фразой, потому что про неё поговорим отдельно ниже.
У Буратино есть только одна зелёная шляпа. Это высказывание легко опровергнуть, если представить, что у Буратино есть две зелёные шляпы и одна синяя:
❌ (есть только одна зелёная шляпа) → (есть две зелёных шляпы и одна синяя) = FALSE
Это значит, что мы не можем сделать вывод «у Буратино есть только одна зелёная шляпа», потому что может быть ситуация, когда у него будут две зелёные и одна синяя шляпа, и при этом он соврёт, сказав, что все его шляпы зелёные.
У Буратино нет шляп. Это самая сложная часть задачи, и здесь нам понадобится математическая логика. По её законам из ложного посыла может следовать что угодно — как истина, так и ложь. Покажем на примере.
❌ У Буратино нет шляп, поэтому все его шляпы зелёные (как в нашем случае) — это может быть истиной, потому что это то же самое, что сказать «У Буратино 0 шляп зелёного цвета». Это будет правдой, потому что у Буратино 0 шляп и все они зелёные.
❌ У Буратино нет шляп, поэтому все его шляпы красные — это тоже может быть истиной, потому что шляпы, которых нет, могут быть любого цвета.
Получается, что мы из этой фразы можем построить два противоположных, но истинных вывода, а это значит, что исходная фраза — ложная. А раз она ложная, то и в качестве вывода мы не сможем её использовать.
У Буратино есть как минимум одна зелёная шляпа. Это можно опровергнуть, представив, что у Буратино две синих шляпы:
❌ (есть как минимум одна зелёная шляпа) → (есть две синих шляпы) = FALSE
Получается, что если Буратино про это соврёт, то наше FALSE превратится в TRUE и Буратино скажет правду, а этого не может быть по условию. Значит, вывод, что у Буратино есть как минимум одна зелёная шляпа, нам не подходит.
У Буратино нет зелёных шляп. Это можно опровергнуть, если представить, что у Буратино есть одна зелёная и одна синяя шляпа:
❌ (нет зелёных шляп) → (есть зелёная и синяя шляпы) = FALSE
Значит, это высказывание нам тоже не подходит.
В итоге из всего перечисленного можно сделать только один вывод, в котором мы точно уверены — у Буратино есть как минимум одна шляпа.