Пятница, самое время финально напрячь голову перед выходными и кайфануть от своей находчивости.
Задача такая: есть 9 заключённых, они располагаются по сетке 3 на 3 внутри квадратного поля. Нарисуйте на этом поле два квадрата, чтобы каждый заключённый оказался изолированным от всех остальных. Обозначьте им личные границы, так сказать.

 Лучшие задачи на нестандартное и логическое мышление
Лучшие задачи на нестандартное и логическое мышление Сложная задача по простой математике для взрослых
Сложная задача по простой математике для взрослых Взрослая задача про монеты со сложными условиями
Взрослая задача про монеты со сложными условиями Две задачи про монеты для людей с нестандартным мышлением
Две задачи про монеты для людей с нестандартным мышлением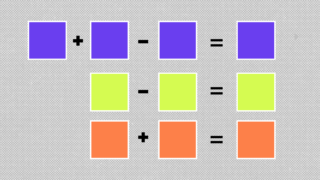 Самая сложная задача для школьников, которую никто не смог решить
Самая сложная задача для школьников, которую никто не смог решить Задача на логику: что в какой коробке?
Задача на логику: что в какой коробке?Кажется, что задача слишком лёгкая, и сходу можно нарисовать пару вариантов, как это решается. Например, так:
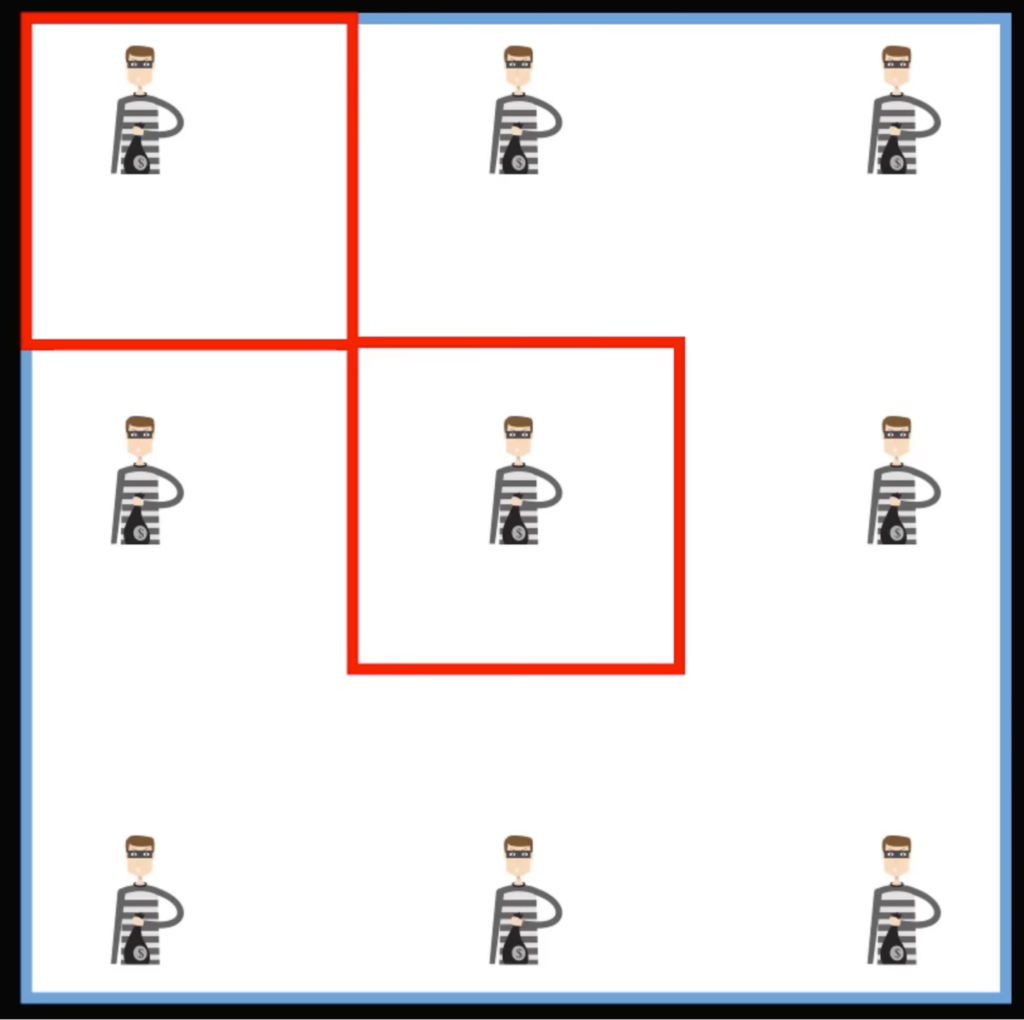
Или так:
Или даже так:
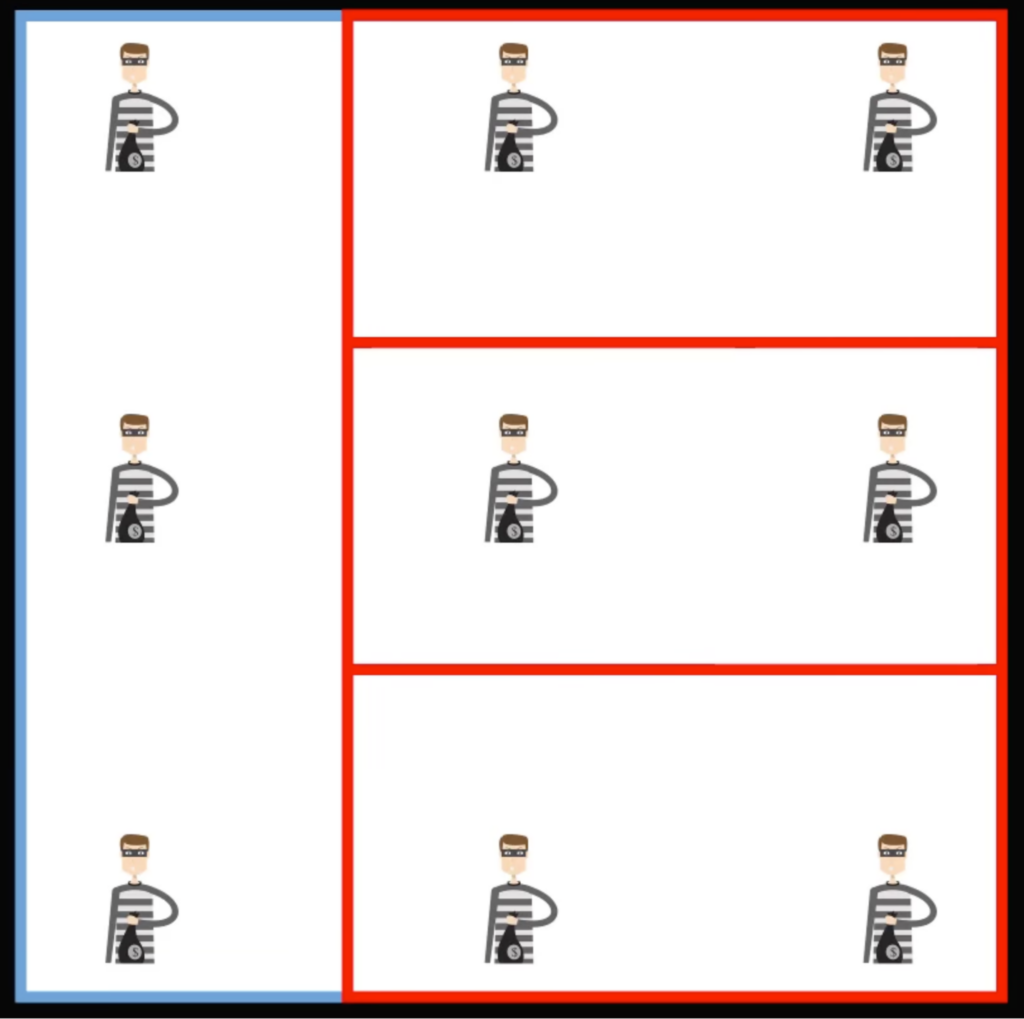
Но если посмотреть на них, то сразу видно, что далеко не все заключённые изолированы друг от друга. Да, есть несколько заключённых, которые оказались отрезаны от других, но во всех примерах всегда остаются несколько человек, которые могут общаться с другими без границ.
Чтобы решить эту задачу, нам нужно выйти за привычные рамки. Чаще всего все тут рисуют квадраты, которые по ориентации сторон совпадают с квадратом поля, где стоят заключённые. Но что если повернуть квадрат на 45 градусов? Например, так:

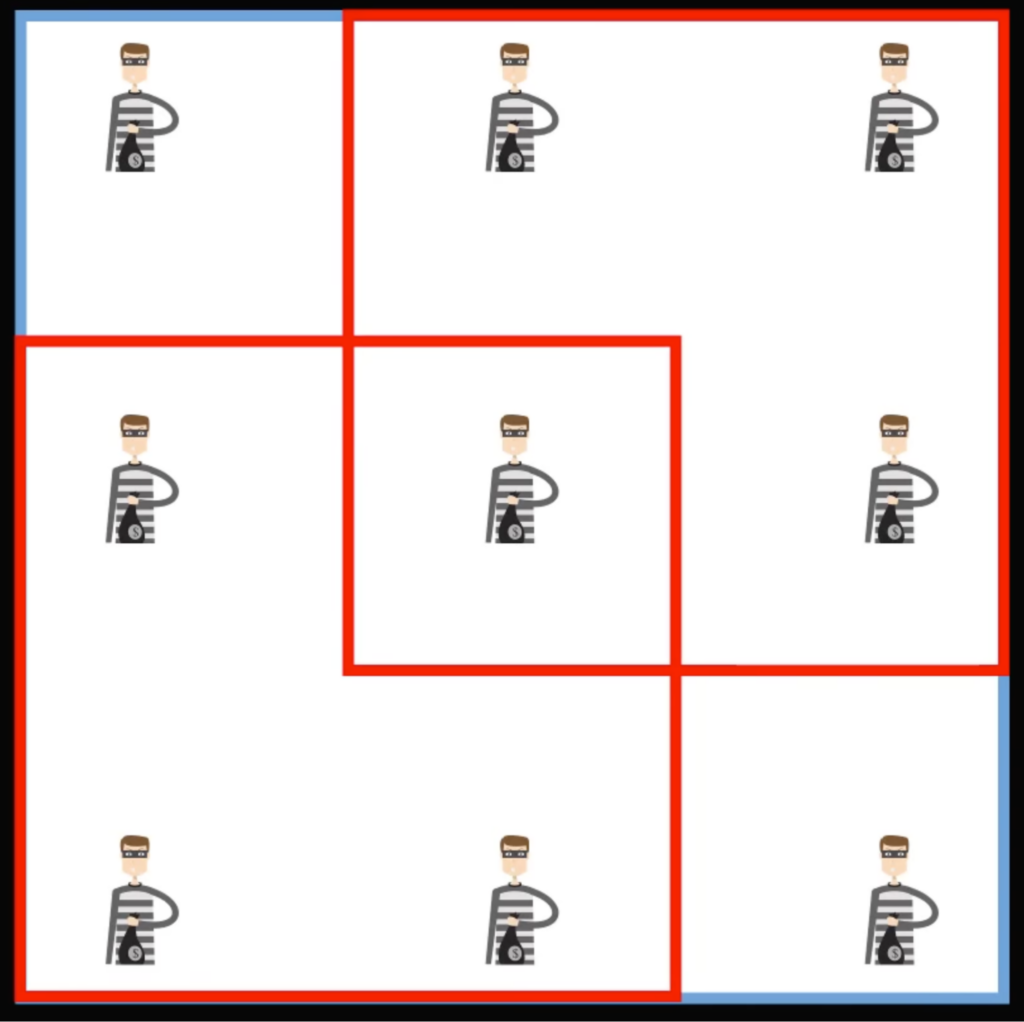
О, у нас получилось так, что угловые заключённые оказались одни, это уже хорошо. Но в центральном квадрате целых 5 человек без границ. А что если вписать в этот квадрат второй? Давайте проверим:
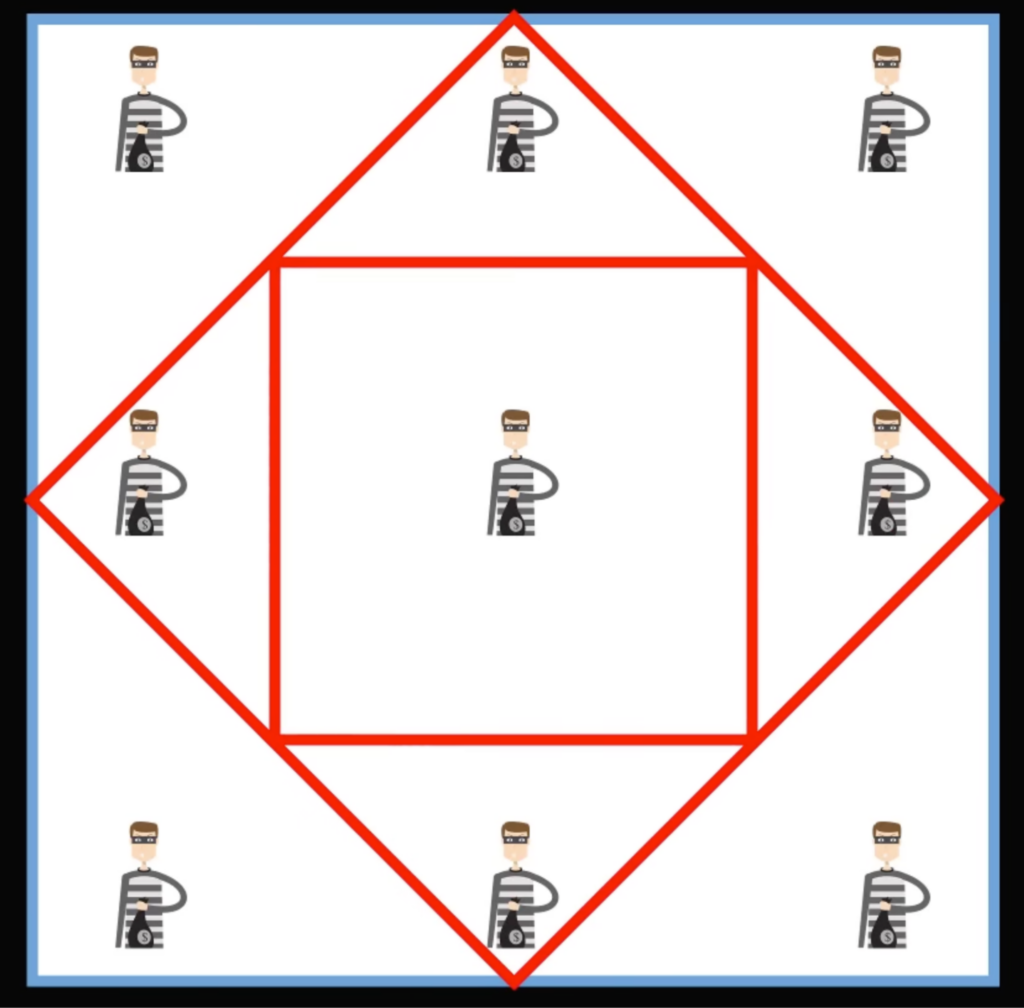
Идеально! Все заключённые оказались изолированы друг от друга.
НО!
Это не единственное решение. Попробуйте найти второе и поделитесь им в комментариях. :)